Geflecht (Mathematik) – Wikipedia

In Mathematik und genauer in der Topologie und Gruppentheorie, a geflochten ist ein mathematisches Objekt, das formalisiert wird, was heißt, geflochten (oder nass ) im Alltag. Die Zöpfe haben eine natürliche Gruppenstruktur und sind tiefgreifende Verbindungen zu verschiedenen Mathematikfeldern, insbesondere in der Topologie, der Theorie von Knoten und algebraischen Kombinationen. Diese Theorie findet Anwendungen in der statistischen Physik, in der Quantenmechanik sowie in theoretischer IT, beispielsweise in der Kryptographie.

Die Geflechtgruppen können auf unterschiedliche Weise definiert werden und veranschaulichen die Beziehungen, die sie zu verschiedenen Bereichen der Mathematik haben.

Geometrische Zöpfe [ Modifikator | Modifikator und Code ]

Entweder

${displayStyle a = links {a_ {1}, …, a_ {n} rechts}}$

eine Menge von

${displayStyle n}$

Offene Einheiten -Festplattenpunkte

${DisplayStyle mathbb {c}}$

.

Wir nennen Brin die Grafik einer Anwendung

${displayStyle b}$

setzt sich fort

${displayStyle i = links [0,1right]}$

in der offenen Einheitscheibe von

${DisplayStyle mathbb {c}}$

, deren endet

${displayStyle b (0)}$

Und

${displayStyle b (1)}$

gehören

${displayStyle a}$

.

Wir nennen Geometrisches Geflecht bei

${displayStyle n}$

Stränge Das Treffen von

${displayStyle n}$

Disjunkte Stränge. Wir sind der Ansicht, dass zwei geometrische Geflecht das gleiche “konzeptionelle” Geflecht darstellen, wenn sie von jedem erhalten werden können, indem die Stränge kontinuierlich bewegt werden, ohne dass sich die Stränge überqueren oder an ihren Enden abheben. Es wird dann gesagt, dass die beiden geometrischen Zöpfe Isotope sind.

Wir definieren ein Kompositionsgesetz für alle geometrischen Zöpfe bei

${displayStyle n}$

Stränge, wie das Produkt von zwei Zöpfen, wird einfach erhalten, indem sie übereinander gestapelt werden. Dieses Produkt ist assoziativ und kompatibel mit der Isotopie -Beziehung. Das Produkt eines Geflechts mit seinem Bild in einem horizontalen Spiegel ist Isotop für das triviale Geflecht (ohne Kreuzung), dessen Äquivalenzklasse die Rolle des neutralen Elements spielt. Dies ermöglicht es daher auch, das Gegenteil eines Geflechts zu definieren. Schließlich ist alle geometrischen Zöpfe bei der Quote der Isotopie eine Gruppe, festgestellt

${displayStyle b_ {n}}$

.

Generatoren und Beziehungen [ Modifikator | Modifikator und Code ]

Die Gruppe der Zöpfe

${displayStyle, b_ {n}}$

Ist die Gruppe von Generatoren generiert?

${displayStyle, Sigma _ {1}, Punkte, Sigma _ {n-1}}$

und Beziehungen

1. 
   $}$

   Anwesend

2. 
   ${displayStyle, Sigma _ {i} Sigma _ {j} = sigma _ {j} sigma _ {i}}$

   Und

   ${DisplayStyle, | i! -! J | Geq 2}$

   .

Grundgruppe [ Modifikator | Modifikator und Code ]

Wir definieren das, was genannt wird Konfigurationsraum

$Oder$

. Mit anderen Worten, dieser Raum ist der Satz von von N -Plets komplexer Zahlen, deren Elemente unterschiedlich sind. Wir können diesen Raum physisch interpretieren, indem wir feststellen, dass eine komplexe Zahl die Koordinaten eines Punktes in einer Ebene darstellt, somit den Konfigurationsraum

${displayStyle, e_ {n}}$

Kann als die Konfigurationsmenge gesehen werden, in der N -Partikel in einer Ebene gefunden werden können (die Bedingung spiegelt einfach die Tatsache wider, dass zwei Partikel nicht an derselben Stelle sein können).

Es wird auch angemerkt, dass die Stränge eines Geflechts im Allgemeinen nicht in der gleichen Reihenfolge wie zu Beginn ankommen. Zum Beispiel kommt bei der ersten Zeichnung der Strang, der von oben links verläuft, unten rechts an. Andererseits gibt es Zöpfe, von denen alle Stränge in die gleiche Position kommen wie die, die sie verlassen haben. Ein solches Geflecht heißt genannt reines Geflecht . Alle reinen Zöpfe bildeten eine Untergruppe der Geflechtgruppe.

Der Zusammenhang zwischen diesen beiden Konzepten ist wie folgt: die grundlegende Gruppe von

${displayStyle, e_ {n}}$

ist die Gruppe reiner Zöpfe zu N Stränge, bemerkt

${displayStyle, p_ {n}}$

.

Bei einer engen Isotopie kann ein abstraktes Geflecht immer durch ein geometrisches Geflecht dargestellt werden, das niemals zwei Kreuzungen auf derselben Höhe enthält. Es ist daher möglich, ein Geflecht in das Flugzeug zu projizieren, um a zu erhalten Geflechtes Diagramm . Um in 3 Dimensionen keine Informationen gegen den Raum zu verlieren, müssen Sie angeben, wenn sich zwei Stränge treffen, die vor dem anderen vorbei sind.

Damit die Geflecht -Diagramme und ihr Produkt Permutationen und ihrer Zusammensetzung entsprechen, müssen Sie die Diagramme von lesen
Bässe von unten nach oben. Zum Beispiel hat das versperrte Diagramm unten die Permutation (1 3 4).

Nehmen wir also zwei Geflecht -Diagramme

${displayStyle, B_ {1}}$

Und

${displayStyle, b_ {2}}$

jeweils assoziierte Permutation

${displayStyle, s_ {1}}$

Und

${displayStyle, s_ {2}}$

. Das Produkt

${displayStyle, b_ {1} b_ {2}}$

hat Permutation

${displayStyle, s_ {1} circ s_ {2}}$

.

Um die Zöpfe zu untersuchen, müssen sie in Bezug auf ihren Weg und ihre damit verbundene Permutation verglichen werden. In einem Geflecht -Diagramm sind einige Kreuzungen unabhängig voneinander.

Zwei Geflecht -Diagramme sollen “Isotope” sein, wenn Sie einen voneinander bekommen können, indem Sie die Stränge bewegen, ohne sie zu “schneiden” und ohne die Enden zu berühren.

Die Isotopie -Beziehung auf

${displayStyle, t_ {n}}$

ist eine Äquivalenzbeziehung.

Zwei Isotopengeflecht -Diagramme repräsentieren dieselbe Permutation, aber die Gegenseitigkeit ist falsch: Zwei Diagramme mit derselben damit verbundenen Permutation sind nicht unbedingt Isotope.

Hier ist wie lange

${displayStyle, t_ {n}}$

Nach der Isotopie -Beziehung erhalten wir eine Gruppenstruktur für alle Geflechtdiagramme

${displayStyle, n}$

Stränge. Wir bemerken

${displayStyle, b_ {n}}$

Und wir nennen “Gruppe von Zöpfen bei N Strängen” die so erhaltene Gruppe. Das neutrale Element ist offensichtlich die Klasse des trivialen Diagramms, die Rückseite eines Diagramms ist das Diagramm, das durch die Aufnahme seines Spiegelbildes erhalten wird, wie wir im folgenden Beispiel sehen.

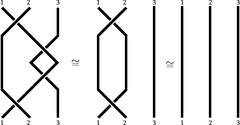
Durch Vereinfachung nennen wir Braid

${displayStyle, n}$

Stränge ein Element von

${displayStyle, b_ {n}}$

.

Wir tauchen

${displayStyle, b_ {n}}$

In

${displayStyle, B_ {n+1}}$

durch Umwandlung von Zöpfen in

${displayStyle, n}$

Geflechte Stränge bei

${displayStyle, n+1}$

Stränge wie folgt.
Wir fügen die rechte A hinzu a

${displayStyle, n+1}$

-Th Strand, der nichts anderes trifft, wie wir im folgenden Beispiel sehen:

Anmerkung

${displayStyle, B_ {Infty}}$

und wir nennen “Gruppe von Zöpfen”, die Gruppe

${DisplayStyle b_ {infty} = bigcup _ {ngeq 0} b_ {n}}$

.

Die Geflechttheorie wird verwendet, um an jedem in der Physik zu beschreiben ^{[ Erste ]} .

Die Geflechttheorie wird in der theoretischen Informatik verwendet, insbesondere im Zusammenhang mit der Theorie von Sprachen und Kryptographie ^{[ 2 ]} .

Es wird auch für bestimmte Jonglierdiagramme verwendet.

In Verbindung stehende Artikel [ Modifikator | Modifikator und Code ]

Literaturverzeichnis [ Modifikator | Modifikator und Code ]

Patrick Dehornoy, « Das Problem der Isotopie von Zöpfen », Die heutigen Mathematikstunden Anwesend vol. 4,, 2010 – Lektion von Marie Albenque geschrieben.

Externer Link [ Modifikator | Modifikator und Code ]

Aurélien Alvarez, ” Bewegte Zöpfe » , An Mathematikbilder Anwesend 2. August 2014 (Interview mit Ester Dalvit)