Locken (Mathematik) – Wikipedia
Kreislaufdichte in einem Vektorfeld

Im Vektorkalkül die Locken ist ein Vektoroperator, der die infinitesimale Zirkulation eines Vektorfeldes im dreidimensionalen euklidischen Raum beschreibt. Die Locken an einem Punkt im Feld wird durch einen Vektor dargestellt, dessen Länge und Richtung die Größe und Achse der maximalen Zirkulation bezeichnen. [Erste] Die Locke eines Feldes wird formal als Zirkulationsdichte an jedem Punkt des Feldes definiert.
Ein Vektorfeld, dessen Curl Null ist, wird als Irrotational bezeichnet. Die Locken ist eine Form der Differenzierung für Vektorfelder. Die entsprechende Form des Grundsatzes des Kalküls ist Stokes ‘Theorem, der das Oberflächenintegral der Locke eines Vektorfeldes auf das Linienintegral des Vektorfelds um die Grenzkurve bezieht.
Locken F ist eine Notation, die heute in den USA und Amerika üblich ist. In vielen europäischen Ländern, insbesondere in der klassischen wissenschaftlichen Literatur, die alternative Notation verrotten F wird traditionell verwendet, das als “Rotor” geschrieben wird und aus der “Rotationsrate” stammt, die es darstellt. Um Verwirrung zu vermeiden, neigen moderne Autoren dazu, die Cross -Produktnotation mit dem DEL -Operator (NABLA) zu verwenden
[2] Dies zeigt auch die Beziehung zwischen Curl (Rotor), Divergenz und Gradientenoperatoren.
Im Gegensatz zum Gradienten und der Divergenz verallgemeinert Curl wie im Vektorkalkül formuliert nicht einfach auf andere Dimensionen. Einige Verallgemeinerungen sind möglich, aber nur in drei Dimensionen ist die geometrisch definierte Krümmung eines Vektorfeldes wieder ein Vektorfeld. Dieser Mangel ist eine direkte Folge der Grenzen des Vektorkalkuls; Andererseits verallgemeinert die Curl auf alle Abmessungen, wenn er als antisymmetrisches Tensorfeld über den Keilbetreiber des geometrischen Kalküls ausgedrückt wird. Der unglückliche Umstand ähnelt dem, der am dreidimensionalen Kreuzprodukt teilnimmt, und in der Tat spiegelt sich die Verbindung in der Notation wider
für die Locken.
Der Name “Curl” wurde erstmals 1871 von James Clerk Maxwell vorgeschlagen [3] Das Konzept wurde jedoch offenbar erstmals bei der Konstruktion einer optischen Feldtheorie von James MacCullagh im Jahr 1839 verwendet. [4] [5]
Definition [ bearbeiten ]
Übereinkommen zur Vektororientierung des Linienintegrals
Die Locken eines Vektorfeldes F , bezeichnet durch Locken F , oder
, oder verrotten F , ist ein Bediener, der kartiert C k Funktionen in R 3 Zu C k –1 Funktionen in R 3 und insbesondere kartiert es kontinuierlich differenzierbare Funktionen R 3 → R 3 zu kontinuierlichen Funktionen R 3 → R 3 . Es kann auf verschiedene Arten definiert werden, um unten zu erwähnen:
Eine Möglichkeit, die Locken eines Vektorfeldes an einem Punkt zu definieren
ist jeder Einheitsvektor, die Projektion der Locken von F auf zu
kann definiert als der begrenzende Wert eines geschlossenen Linienintegrals in einer Ebene orthogonal zu
geteilt durch den beitifizierten Bereich, da der Integrationsweg auf unbestimmte Zeit um den Punkt erfasst wird.
Insbesondere wird die Locken an einem Punkt definiert P als [6] [7]
wo das Linienintegral entlang der Grenze berechnet wird C Der Fläche A fraglich, | A | die Größe des Gebiets sein. Diese Gleichung definiert die Projektion der Locke von F auf zu
. Die infinitesimalen Oberflächen von begrenzt von C haben
als normal. C ist über die rechte Regel ausgerichtet.
Die obige Formel bedeutet, dass die Projektion der Locken eines Vektorfeldes entlang einer bestimmten Achse die ist Infinitesimale Flächendichte der Zirkulation des Feldes auf eine Ebene senkrecht zu dieser Achse projiziert. Diese Formel nicht Erste Definieren Sie ein legitimes Vektorfeld für die einzelnen Zirkulationsdichten in Bezug auf verschiedene Achsen Erste muss sich nicht auf die gleiche Weise wie die Komponenten eines Vektors beziehen; daß sie Tun In dieser genauen Weise muss sich auf diese Weise beziehen.
Zu dieser Definition passt natürlich der Theorem von Kelvin -Stokes als eine globale Formel, die der Definition entspricht. Es entspricht dem Oberflächenintegral der Locke eines Vektorfeldes mit dem oben genannten Integral der Oberfläche.
Eine andere Möglichkeit, den Lockenvektor einer Funktion zu definieren F An einem Punkt ist explizit als der begrenzende Wert eines von Vektor bewerteten Oberflächenintegrals um eine Schale umschließt P geteilt durch das umschlossen P .
Insbesondere kann die Locken durch die Vektorformel definiert werden
wobei das Oberflächenintegral entlang der Grenze berechnet wird S des Volumens IN Anwesend | IN | die Größe des Volumens sein, und
nach außen von der Oberfläche zeigen S an jedem Punkt senkrecht S .
In dieser Formel misst das Kreuzprodukt im Integrand die tangentiale Komponente von F an jedem Punkt auf der Oberfläche S zusammen mit der Ausrichtung dieser tangentialen Komponenten in Bezug auf die Oberfläche S . Somit misst das Oberflächenintegral das allgemeine Ausmaß, in dem F zirkuliert herum S zusammen mit der Nettoorientierung dieser Kreislauf im Raum. Der Locken eines Vektorfeldes an einem Punkt dann die dann die Infinitesimale Volumendichte des Netzes Vektor Zirkulation (d. H. Sowohl Größe als auch räumliche Ausrichtung) des Feldes um den Punkt.
Zu dieser Definition passt natürlich zu einer anderen globalen Formel (ähnlich dem Kelvin-Stokes-Theorem), der das Volumenintegral der Locke eines Vektorfeldes mit dem über die Grenze des Volumes übernommenen Oberflächenintegrals gleichgibt.
Während die beiden oben genannten Definitionen der Curl kostenlos sind, gibt es eine weitere “leicht merktorisierende” Definition der Locken in krummlinaren orthogonalen Koordinaten, z. In kartesischen Koordinaten sphärische, zylindrische oder sogar elliptische oder parabolische Koordinaten:
Die Gleichung für jede Komponente (Curl F ) k kann durch den Austausch jedes Auftretens eines Index 1, 2, 3 in der zyklischen Permutation erhalten werden: 1 → 2, 2 → 3 und 3 → 1 (wobei die Indexs die relevanten Indizes darstellen).
Wenn ( X Erste Anwesend X 2 Anwesend X 3 ) sind die kartesischen Koordinaten und ( In Erste Anwesend In 2 Anwesend In 3 ) sind die orthogonalen Koordinaten dann
ist die Länge des Koordinatenvektors, der entspricht In ich . Die verbleibenden zwei Komponenten von Curl ergeben sich aus der zyklischen Permutation von Indizes: 3,1,2 → 1,2,3 → 2,3,1.
Intuitive Interpretation [ bearbeiten ]
Angenommen, das Vektorfeld beschreibt das Geschwindigkeitsfeld eines Flüssigkeitsstroms (wie ein großer Flüssigkeits- oder Gasentank) und eine kleine Kugel befindet sich innerhalb des Fluids oder des Gases (der Mitte der Kugel, die an einem bestimmten Punkt fixiert ist). Wenn die Kugel eine raue Oberfläche aufweist, wird die Flüssigkeit, die vorbei fließt, sie dreht. Die Rotationsachse (nach der rechten Regel ausgerichtet) zeigt in Richtung des Feldes des Feldes in der Mitte der Kugel, und die Winkelgeschwindigkeit der Drehung ist die Hälfte der Größe der Locken an diesem Punkt. [8]
Die Locke des Vektors an jedem Punkt wird durch die Rotation eines infinitesimalen Bereichs in der gegeben xy -plane (für Mit -Axiskomponente der Locken), ZX -plane (für Und -Axiskomponente der Locken) und yz -plane (für X -Axiskomponente des Lockenvektors). Dies ist deutlich in den folgenden Beispielen zu sehen.
In der Praxis werden die beiden oben beschriebenen koordinatenfreien Definitionen selten verwendet, da in praktisch allen Fällen der Curl-Operator unter Verwendung einer Reihe von krummlinigen Koordinaten angewendet werden kann, für die einfachere Darstellungen abgeleitet wurden.
Die Notation ∇ × F hat seinen Ursprung in den Ähnlichkeiten mit dem dreidimensionalen Kreuzprodukt und ist als Mnemonik in kartesischen Koordinaten nützlich, wenn ∇ wird als Vektor -Differentialbetreiber del angenommen. Eine solche Notation, an der Operatoren beteiligt sind, ist in Physik und Algebra häufig.
In dreidimensionalen kartesischen Koordinaten erweitert (siehe Del in zylindrischen und sphärischen Koordinaten für sphärische und zylindrische Koordinatenrepräsentationen), ∇ × F ist für F zusammengesetzt aus [ F X Anwesend F Und Anwesend F Mit ] (Wenn die Indexs die Komponenten des Vektors angeben, nicht teilweise Ableitungen):
Wo ich Anwesend J , Und k sind die Einheitsvektoren für die X -,, Und -, Und Mit -Axes. Dies erweitert sich wie folgt: [9] : 43
Obwohl sie in Bezug auf Koordinaten ausgedrückt werden, ist das Ergebnis unter ordnungsgemäßen Rotationen der Koordinatenachsen inverlösend, aber die resultierenden Inverts unter Reflexion.
In einem allgemeinen Koordinatensystem wird die Locken gegeben [Erste]
Wo e Bezeichnet den Levi-Civita-Tensor, ∇ das kovariante Derivat,
ist die Determinante des metrischen Tensors und die Einstein -Summierungskonvention impliziert, dass wiederholte Indizes summiert werden. Aufgrund der Symmetrie der an der kovarianten Derivat beteiligten Christoffel -Symbole reduziert sich dieser Ausdruck auf das partielle Ableitungen:
Wo R k sind die lokalen Basisvektoren. Äquivalent kann die Locke unter Verwendung des äußeren Derivats als:
Hier ♭ Und ♯ sind die musikalischen Isomorphismen und ★ ist der Hodge Star -Operator. Diese Formel zeigt, wie die Locke von berechnet werden kann F In jedem Koordinatensystem und wie die Locken auf einen orientierten dreidimensionalen Riemannschen Verteiler ausgeweitet werden. Da dies von einer Auswahl der Orientierung abhängt, ist Curl eine chirale Operation. Mit anderen Worten, wenn die Ausrichtung umgekehrt ist, ist auch die Richtung der Locken umgekehrt.
Beispiele [ bearbeiten ]
Vektorfeld F (x, y) = [y, -x] (links) und seine Locken (rechts).
Beispiel 1 [ bearbeiten ]
Das Vektorfeld
kann als zerlegt werden als
Bei visueller Inspektion kann das Feld als “rotierend” beschrieben werden. Wenn die Vektoren des Feldes eine lineare Kraft darstellen würden, die auf an diesem Punkt vorhandene Objekte wirkt, und ein Objekt im Feld platziert werden sollte, würde das Objekt im Uhrzeigersinn um sich selbst drehen. Dies gilt unabhängig davon, wo das Objekt platziert ist.
Berechnung der Locken:
Das resultierende Vektorfeld, das die Curl beschreibt, würde auf alle Punkte negativ zeigen Mit Richtung. Die Ergebnisse dieser Gleichung übereinstimmen mit dem, was mit der rechten Regel unter Verwendung eines rechtshändigen Koordinatensystems hätte vorhergesagt werden können. Da das zuvor beschriebene Objekt ein einheitliches Vektorfeld ist, hätte es die gleiche Rotationsintensität, unabhängig davon, wo es platziert wurde.
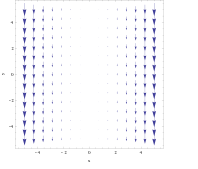
Vektorfeld F (x, y) = [0, – X 2 ] (links) und seine Locken (rechts).
Beispiel 2 [ bearbeiten ]
Für das Vektorfeld
Die Locken ist nicht so offensichtlich aus der Grafik. Nehmen Sie das Objekt jedoch im vorherigen Beispiel ein und platzieren Sie es überall in der Leitung X = 3 Die auf der rechte Seite ausgeübte Kraft wäre geringfügig größer als die links ausgeübte Kraft, wodurch sie im Uhrzeigersinn dreht. Unter Verwendung der rechten Regel kann vorausgesagt werden, dass die resultierende Curl im Negativ geraden wäre Mit Richtung. Umgekehrt, wenn X = –3 Das Objekt würde gegen den Uhrzeigersinn drehen und die rechte Regel würde zu einem positiven führen Mit Richtung.
Berechnung der Locken:
Die Lockenpunkte im Negativpunkt Mit Richtung wann X ist positiv und umgekehrt. In diesem Feld wäre die Drehungsintensität größer, wenn sich das Objekt von der Ebene weg bewegt X = 0 .
Beschreibende Beispiele [ bearbeiten ]
- In einem Vektorfeld, das die linearen Geschwindigkeiten jedes Teils einer rotierenden Scheibe beschreibt, hat die Curl an allen Punkten den gleichen Wert, und dieser Wert ist genau das Zweifache der vektorialen Winkelgeschwindigkeit der Scheibe (wie üblich nach rechts ausgerichtet -Handregel). Im Allgemeinen hat für jede fließende Masse das Feld der linearen Geschwindigkeitsvektor an jedem Punkt des Massenfluss lokal Vektoriale Winkelgeschwindigkeit der Masse über den Punkt.
- Für jedes feste Objekt, das einer externen physikalischen Kraft (wie der Schwerkraft oder der elektromagnetischen Kraft) unterliegt, kann das Vektorfeld in Betracht ziehen, das die infinitesimalen Kraft-pro-Einheit-Barrungsbeiträge darstellt, die an jedem der Punkte des Objekts wirken. Dieses Kraftfeld kann ein Netz erzeugen Drehmoment Auf dem Objekt über sein Massenzentrum und dieses Drehmoment stellt sich als direkt proportional und vektrisch parallel zum (vektor betrachteten) Integral der Locken des Kraftfeldes über das gesamte Volumen.
- Von den vier Maxwell -Gleichungen können zwei – Faraday’s Law und Ampère’s Law – mit Curl kompakt ausgedrückt werden. Das Gesetz von Faraday besagt, dass die Locke eines elektrischen Feldes gleich dem Gegenteil der zeitlichen Änderung des Magnetfeldes entspricht, während das Gesetz von Ampère die Locke des Magnetfelds auf den Strom und die zeitliche Änderungsrate des elektrischen Feldes bezieht.
Identitäten [ bearbeiten ]
Im Allgemeinen krummlinige Koordinaten (nicht nur in kartesischen Koordinaten), die Locke eines Kreuzprodukts von Vektorfeldern In Und F kann gezeigt werden
Austausch des Vektorfeldes In Und ∇ Betreiber kommen wir zum Querprodukt eines Vektorfeldes mit Curl eines Vektorfeldes:
Wo ∇ F ist die Feynman -Index -Notation, die nur die Variation aufgrund des Vektorfelds berücksichtigt F (d. H. In diesem Fall, In wird im Raum als konstant behandelt).
Ein weiteres Beispiel ist die Locke einer Locke eines Vektorfeldes. Es kann gezeigt werden, dass im Allgemeinen Koordinaten
und diese Identität definiert den Vektor -Laplacianer von F , symbolisiert als ∇ 2 F .
Die Locken des Gradienten von beliebig Skalarfeld Phi ist immer das Feld Null Vektor
was aus der Antisymmetrie in der Definition der Locken und der Symmetrie der zweiten Derivate folgt.
Die Divergenz der Locken eines Vektorfeldes ist gleich Null:
Wenn Phi ist eine skalargeschätzte Funktion und F ist dann ein Vektorfeld
Verallgemeinerungen [ bearbeiten ]
Die Vektorkalküloperationen von Grad, Curl und DIV sind im Kontext von Differentialformen, die eine Reihe von Schritten beinhalten, am einfachsten verallgemeinert. Kurz gesagt, sie entsprechen den Derivaten von 0-Forms, 1-Forms bzw. 2-Forms. Die geometrische Interpretation von Curl als Rotation entspricht der Identifizierung von Bivektoren (2-Vektoren) in 3 Dimensionen mit der speziellen orthogonalen Lie-Algebra
(3) von infinitesimalen Rotationen (in Koordinaten, schief symmetrische 3 × 3-Matrizen), während die Darstellung von Rotationen durch Vektoren 1-Vektoren (äquivalent 2-Vektoren) und identifiziert werden
(3) Diese sind alle dreidimensionale Räume.
Differentialformen [ bearbeiten ]
In 3 Dimensionen ist eine differentielle 0-Form einfach eine Funktion F ( X Anwesend Und Anwesend Mit ) ; Eine differentielle 1-Form ist der folgende Ausdruck, bei dem die Koeffizienten Funktionen sind:
Eine differentielle 2-Form ist die formale Summe, wiederum mit Funktionskoeffizienten:
und eine differentielle 3-Form wird durch einen einzelnen Begriff mit einer Funktion als Koeffizient definiert:
(Hier das A -Coefficients sind echte Funktionen von drei Variablen; Die “Keilprodukte”, z. dx ∧ diese , kann als eine Art orientierte Flächenelemente interpretiert werden, dx ∧ diese = – diese ∧ dx , usw.)
Die Außenableitung von a k -Form in R 3 ist definiert als die ( k + 1) -Form von oben -und in R N Wenn, z. B.,
dann das Außenableitungsmittel D führt zu
Die Außenableitung einer 1-Form ist daher eine 2-Form, und die einer 2-Form ist eine 3-Form. Andererseits aufgrund der Austauschbarkeit gemischter Derivate, z. wegen
Die zweifache Anwendung des Außenderivats führt zu 0.
Daher bezeichnet der Raum von k -Forms von Oh k ( R 3 ) und das äußere Derivat durch D Man erhält eine Sequenz:
Hier Oh k ( R N ) ist der Raum der Abschnitte der Außenalgebra L k ( R N ) Vektorbündel vorbei R N , deren Dimension der Binomialkoeffizient ist ( N
k ) ; beachten Sie, dass Oh k ( R 3 ) = 0 für k > 3 oder k <0 . Wenn man nur Dimensionen schreibt, erhält man eine Reihe von Pascals Dreieck:
- 0 → 1 → 3 → 1 → 0;
Die 1-dimensionalen Fasern entsprechen Skalarfeldern und die dreidimensionalen Fasern zu Vektorfeldern, wie nachstehend beschrieben. Modulo -geeignete Identifikationen, die drei nichttrivialen Vorkommen des Außenableitungs entsprechen Grad, Curl und Div.
Differentielle Formen und das Differential können auf jedem euklidischen Raum oder in der Tat ein Verteiler ohne Vorstellung einer riemannischen Metrik definiert werden. Auf einem Riemannschen Verteiler oder allgemeiner pseudo-riemanner Verteiler, k -Forms können mit identifiziert werden k -Vektorfelder ( k -Forms sind k -Covector-Felder und eine pseudo-riemannische Metrik liefert einen Isomorphismus zwischen Vektoren und Kovektoren) und auf einem orientiert Vektorraum mit einer nicht genannten Form (einem Isomorphismus zwischen Vektoren und Kovektoren) liegt ein Isomorphismus zwischen k -Vektoren und ( N – – k ) -Vektoren; insbesondere auf (den Tangentenraum) einem orientierten Pseudo-riemannischen Verteiler. So kann man auf einem orientierten Pseudo-Riemannschen Verteiler austauschen k -Formen, k -Vektorfelder, ( N – – k ) -Forms und ( N – – k ) -Vektorfelder; Dies ist als Hodge Dualität bekannt. Konkret auf R 3 Dies ist gegeben durch:
- 1-forms- und 1-Vektorfelder: die 1-Form A X dx + A Und diese + A Mit DZ entspricht dem Vektorfeld ( A X Anwesend A Und Anwesend A Mit ) .
- 1-forms und 2-forms: man ersetzt dx durch die doppelte Menge diese ∧ DZ (d.h., weglassen dx ), und gleichzeitig kümmern sich um die Orientierung: diese entspricht DZ ∧ dx = – dx ∧ DZ , Und DZ entspricht dx ∧ diese . So die Form A X dx + A Und diese + A Mit DZ entspricht der “Dualform” A Mit dx ∧ diese + A Und DZ ∧ dx + A X diese ∧ DZ .
Somit identifizieren Sie 0-forms und 3-forms mit skalaren Feldern sowie 1-forms und 2-forms mit Vektorfeldern:
- Grad nimmt ein Skalarfeld (0-Form) in ein Vektorfeld (1-Form);
- Curl nimmt ein Vektorfeld (1-Form) in ein Pseudovektorfeld (2-Form);
- Div nimmt ein Pseudovektorfeld (2-Form) in ein Pseudoscalar-Feld (3-Form).
Andererseits die Tatsache, dass das D 2 = 0 entspricht den Identitäten
Für jedes skalare Bereich F , Und
für jeden Vektorbereich In .
Grad und Div verallgemeinern alle orientierten Pseudo-riemannischen Verteiler mit der gleichen geometrischen Interpretation, weil die Räume von 0 Formularen und N -Formen an jedem Punkt sind immer 1-dimensional und können mit skalaren Feldern identifiziert werden, während die Räume von 1-forms und ( N – 1) -Forms sind immer faserzeigert N -Dimensional und kann mit Vektorfeldern identifiziert werden.
Curl verallgemeinert auf diese Weise nicht auf 4 oder mehr Dimensionen (oder bis zu 2 oder weniger Dimensionen). In 4 Dimensionen sind die Abmessungen
- 0 → 1 → 4 → 6 → 4 → 1 → 0;
Daher ist die Locke eines 1-Vektorfeldes (faserweise 4-dimensional) a 2-Vektorfeld , was an jedem Punkt zum 6-dimensionalen Vektorraum gehört, und so hat man
Dies ergibt eine Summe von sechs unabhängigen Begriffen und kann nicht mit einem 1-Vektor-Feld identifiziert werden. Man kann auch nicht sinnvoll von einem 1-Vektor-Feld zu einem 2-Vektorfeld zu einem 3-Vektor-Feld (4 → 6 → 4) wechseln, da das Differential zweimal Null nimmt ( D 2 = 0 ). Somit gibt es keine Curl -Funktion von Vektorfeldern zu Vektorfeldern in anderen Dimensionen, die auf diese Weise entstehen.
Man kann jedoch eine Locke eines Vektorfelds als a definieren 2-Vektorfeld Im Allgemeinen, wie unten beschrieben.
Locken geometrisch [ bearbeiten ]
2-Vektoren entsprechen der Außenkraft L 2 IN ; In Gegenwart eines inneren Produkts sind dies in Koordinaten die schief symmetrischen Matrizen, die geometrisch als spezielle orthogonale Lügenalgebra angesehen werden
( IN ) von infinitesimalen Rotationen. Das hat ( N
2 ) = Erste / 2 N ( N – 1) Dimensionen und ermöglicht es, das Differential eines 1-Vektorfeldes als seine infinitesimalen Rotationen zu interpretieren. Nur in 3 Dimensionen (oder trivial in 0 Dimensionen) haben wir N = Erste / 2 N ( N – 1) , was der eleganteste und gemeinsamste Fall ist. In 2 Dimensionen ist die Krümmung eines Vektorfeldes kein Vektorfeld, sondern eine Funktion, da zweidimensionale Rotationen durch einen Winkel angegeben sind (ein Skalar-eine Ausrichtung ist erforderlich, um zu wählen, ob man im Uhrzeigersinn oder gegen den Uhrzeigersinn als positiv zählt); Dies ist nicht die DIV, sondern eher senkrecht. In 3 Dimensionen ist die Locke eines Vektorfeldes ein Vektorfeld, wie es bekannt ist (in 1 und 0 Dimensionen ist die Locke eines Vektorfeldes 0, da es keine nicht trivialen 2-Vektoren gibt), während in 4 Dimensionen die Lock Ein Vektorfeld ist geometrisch an jedem Punkt ein Element der 6-dimensionalen Lügealgebra
.
Die Locken eines dreidimensionalen Vektorfelds, das nur von 2 Koordinaten abhängt (z. B. X Und Und ) ist einfach ein vertikales Vektorfeld (in der Mit Richtung), deren Größe die Locken des 2-dimensionalen Vektorfeldes ist, wie in den Beispielen auf dieser Seite.
Die Betrachtung von Curl als 2-Vektor-Feld (ein antisymmetrischer 2-Tensor) wurde verwendet, um den Vektorrechnung und die damit verbundene Physik auf höhere Dimensionen zu verallgemeinern. [zehn]
Umgekehrt [ bearbeiten ]
In dem Fall, in dem die Abweichung eines Vektorfeldes IN ist Null, ein Vektorfeld IN existiert so, dass IN = curl ( IN ) . [ Zitat benötigt ] Aus diesem Grund kann das Magnetfeld, das durch Null -Divergenz gekennzeichnet ist, als die Locke eines Magnetvektorpotentials ausgedrückt werden.
Wenn IN ist ein Vektorfeld mit Locken ( IN ) = IN und dann ein Fachgebiet des Gradientenvektors hinzufügen Grad ( F ) Zu IN wird zu einem anderen Vektorfeld führen IN + Grad ( F ) so dass Locken ( IN + Grad ( F )) = IN sowie. Dies kann zusammengefasst werden, indem die inversen Locken eines dreidimensionalen Vektorfeldes bis zu einem unbekannten irrotationalen Feld mit dem Biot-Savart-Gesetz erhalten werden kann.
Siehe auch [ bearbeiten ]
Verweise [ bearbeiten ]
- ^ A B Weepstein, Eric W. “Locken” . Mathord .
- ^ ISO/IEC 80000-2 Standard Norm ISO/IEC 80000-2, Artikel 2-17.16
- ^ Proceedings of the London Mathematical Society, 9. März 1871
- ^ Gesammelte Werke von James Maccullagh
- ^ Früheste bekannte Verwendungen einiger der Wörter der Mathematik tripod.com
- ^ Mathematische Methoden für Physik und Ingenieurwesen, K.F. Riley, M.P. Hobson, S.J. Bence, Cambridge University Press, 2010, ISBN 978-0-521-86153-3
- ^ Vector Analysis (2nd Edition), M.R. Spiegel, S. Lipschutz, D. Spellman, Schaum’s Outlines, McGraw Hill (USA), 2009, ISBN 978-0-07-161545-7
- ^ Gibbs, Josiah Willard; Wilson, Edwin Bidwell (1901), Vektoranalyse , Yale Bicentennial Publications, C. Scribners Söhne, HDL: 2027/MDP.39015000962285
- ^ Arfken, George Brown (2005). Mathematische Methoden für Physiker . Weber, Hans-Jürgen (6. Aufl.). Boston: Elsevier. ISBN 978-0-08-047069-6 . OCLC 127114279 .
- ^ McDavid, A. W.; McMullen, C. D. (2006-10-30). “Verallgemeinerung von Cross -Produkten und Maxwells Gleichungen auf universelle zusätzliche Dimensionen”. Arxiv: HEP-PH/0609260 .
Weitere Lesen [ bearbeiten ]
Externe Links [ bearbeiten ]
 [2] Dies zeigt auch die Beziehung zwischen Curl (Rotor), Divergenz und Gradientenoperatoren.
[2] Dies zeigt auch die Beziehung zwischen Curl (Rotor), Divergenz und Gradientenoperatoren.  für die Locken.
für die Locken. 




 ist jeder Einheitsvektor, die Projektion der Locken von
ist jeder Einheitsvektor, die Projektion der Locken von 

![{displaystyle {begin{aligned}&(operatorname {curl} mathbf {F} )_{1}={frac {1}{h_{2}h_{3}}}left({frac {partial (h_{3}F_{3})}{partial u_{2}}}-{frac {partial (h_{2}F_{2})}{partial u_{3}}}right),\[5pt]&(operatorname {curl} mathbf {F} )_{2}={frac {1}{h_{3}h_{1}}}left({frac {partial (h_{1}F_{1})}{partial u_{3}}}-{frac {partial (h_{3}F_{3})}{partial u_{1}}}right),\[5pt]&(operatorname {curl} mathbf {F} )_{3}={frac {1}{h_{1}h_{2}}}left({frac {partial (h_{2}F_{2})}{partial u_{1}}}-{frac {partial (h_{1}F_{1})}{partial u_{2}}}right).end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72c5af513489cd914b40cf463007656bc9a9cd3c)

![{displaystyle nabla times mathbf {F} ={begin{vmatrix}{boldsymbol {hat {imath }}}&{boldsymbol {hat {jmath }}}&{boldsymbol {hat {k}}}\[5pt]{dfrac {partial }{partial x}}&{dfrac {partial }{partial y}}&{dfrac {partial }{partial z}}\[10pt]F_{x}&F_{y}&F_{z}end{vmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7cb295cbe1c98d362263a79bc541e3091f7e6405)


 ist die Determinante des metrischen Tensors und die Einstein -Summierungskonvention impliziert, dass wiederholte Indizes summiert werden. Aufgrund der Symmetrie der an der kovarianten Derivat beteiligten Christoffel -Symbole reduziert sich dieser Ausdruck auf das partielle Ableitungen:
ist die Determinante des metrischen Tensors und die Einstein -Summierungskonvention impliziert, dass wiederholte Indizes summiert werden. Aufgrund der Symmetrie der an der kovarianten Derivat beteiligten Christoffel -Symbole reduziert sich dieser Ausdruck auf das partielle Ableitungen: 















 (3) von infinitesimalen Rotationen (in Koordinaten, schief symmetrische 3 × 3-Matrizen), während die Darstellung von Rotationen durch Vektoren 1-Vektoren (äquivalent 2-Vektoren) und identifiziert werden
(3) von infinitesimalen Rotationen (in Koordinaten, schief symmetrische 3 × 3-Matrizen), während die Darstellung von Rotationen durch Vektoren 1-Vektoren (äquivalent 2-Vektoren) und identifiziert werden 









 .
.
Recent Comments