The Chow-Test is a statistical test with which the coefficients of two linear regressions can be tested for equality. The test is named after its inventor, the economist Gregory Chow.
The CHOW test is used in economics to test time series on structural fractures. Another area of application is the programvaluation, here two different sub -groups (programs), such as two school types, are compared. In contrast to the time series analysis, the two subgroups cannot be assigned to any consecutive intervals, instead the division is made according to a qualitative aspect, such as the school type.
There is a data set
 with
with
 for
for
 whose relationship through a linear function with a normal distributed error (
whose relationship through a linear function with a normal distributed error (
 ) with expectation value 0 (
) with expectation value 0 (
 ) is described (multiple regression analysis), i.e. H. One has
) is described (multiple regression analysis), i.e. H. One has
-
 for
for
 .
.
However, one suspects that the data record is in two groups of the sizes
 and
and
 Division, which are better described by two different linear functions.
Division, which are better described by two different linear functions.
-
 for
for

-
 for
for

Here is
 And it becomes the hypothesis
And it becomes the hypothesis
 against
against
 tested. If one refers to the sum of the square residues of the regression over the entire data set
tested. If one refers to the sum of the square residues of the regression over the entire data set
 and with the two sub -groups with
and with the two sub -groups with
 and
and
 , then the test size defined below follows
, then the test size defined below follows
 an F distribution with the degrees of freedom
an F distribution with the degrees of freedom
 and
and
 .
.
-

The following data record is given, the relationship of which is due to the linear function
 should be modeled:
should be modeled:
 |
0.5 |
1.0 |
1.5 |
2.0 |
2.5 |
3.0 |
3.5 |
4.0 |
4.5 |
5.0 |
5.5 |
6.0 |
 |
−0.043 |
0.435 |
0.149 |
0.252 |
0.571 |
0.555 |
0.678 |
3,119 |
2.715 |
3.671 |
3.928 |
3,962 |
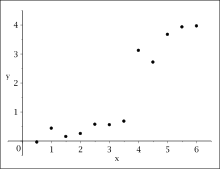
The data plot sets a structural fracture

vicinity.
A data plot suggests that at
 There is a structure of a structural fraction, so the data record is divided into 2 intervals
There is a structure of a structural fraction, so the data record is divided into 2 intervals
![{displaystyle [0{,}5;3{,}5]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb339edbbc76122ec6a8c9bfcd05b892da3f25c7) and
and
![{displaystyle [4{,}0;6{,}0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f6bf512f84431a3576263290e0cafdbe76a655e) and runs separate regressions via this, in addition to regression over the entire data record. Then you test whether the two sub -regressions create the same linear function, i.e.
and runs separate regressions via this, in addition to regression over the entire data record. Then you test whether the two sub -regressions create the same linear function, i.e.
 against
against

Regression on the entire data record:
 |
 |
 |
 |
 |
 |
Regression on
![{displaystyle [0{,}5,3{,}5]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ab416f90870c2504116332118f1890776a14d37)
 |
 |
 |
 |
 |
 |
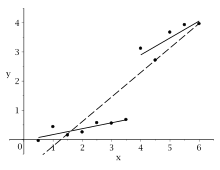
Data plot with regression line
Regression on
![{displaystyle [4{,}0,6{,}0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18af0b593226e3d363819933d712a88c1249c23d)
 |
 |
 |
 |
 |
 |
Calculation of the test size:
-

Because of
 (Significance level
(Significance level
 ) is applicable
) is applicable
 . So the null hypothesis can
. So the null hypothesis can
 be rejected. This means that the two regression straight on the partial intervals are not identical. So there is a structure of the structure and the partial regressions provide better modeling than regression over the entire data set.
be rejected. This means that the two regression straight on the partial intervals are not identical. So there is a structure of the structure and the partial regressions provide better modeling than regression over the entire data set.


 with
with  for
for  whose relationship through a linear function with a normal distributed error (
whose relationship through a linear function with a normal distributed error (  ) with expectation value 0 (
) with expectation value 0 (  ) is described (multiple regression analysis), i.e. H. One has
) is described (multiple regression analysis), i.e. H. One has 
 and
and  Division, which are better described by two different linear functions.
Division, which are better described by two different linear functions. 



 And it becomes the hypothesis
And it becomes the hypothesis  against
against  tested. If one refers to the sum of the square residues of the regression over the entire data set
tested. If one refers to the sum of the square residues of the regression over the entire data set  and with the two sub -groups with
and with the two sub -groups with  and
and  , then the test size defined below follows
, then the test size defined below follows  an F distribution with the degrees of freedom
an F distribution with the degrees of freedom  and
and  .
. 
 should be modeled:
should be modeled: 


![{displaystyle [0{,}5;3{,}5]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb339edbbc76122ec6a8c9bfcd05b892da3f25c7) and
and ![{displaystyle [4{,}0;6{,}0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f6bf512f84431a3576263290e0cafdbe76a655e) and runs separate regressions via this, in addition to regression over the entire data record. Then you test whether the two sub -regressions create the same linear function, i.e.
and runs separate regressions via this, in addition to regression over the entire data record. Then you test whether the two sub -regressions create the same linear function, i.e.  against
against 






![{displaystyle [0{,}5,3{,}5]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ab416f90870c2504116332118f1890776a14d37)






![{displaystyle [4{,}0,6{,}0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18af0b593226e3d363819933d712a88c1249c23d)







 (Significance level
(Significance level  ) is applicable
) is applicable  . So the null hypothesis can
. So the null hypothesis can  be rejected. This means that the two regression straight on the partial intervals are not identical. So there is a structure of the structure and the partial regressions provide better modeling than regression over the entire data set.
be rejected. This means that the two regression straight on the partial intervals are not identical. So there is a structure of the structure and the partial regressions provide better modeling than regression over the entire data set.
Recent Comments