Theorem of the inscribed angle and the angle in the center – Wikipedia

Posted on by
before-content-x4

Figure 1: The AOB angle measures the double of the AMB angle and the anb angle.

Figure 2: Ambtus inscribed angle, angle in the home center.

In Euclidean geometry hovers, more precisely in the geometry of the circle, the Theorems of the inscribed angle and the angle in the center establish relations linking the enrolled angles [ first ] And the angles in the center intercepting the same arch.

  • The Angle theorem in the center says that, in a circle, an angle in the center measures the double of an inscribed angle intercepting the same arc (Figure 1 and 2,

    ).

  • The Theorem of the inscribed angle is a consequence of the previous one and affirms that two registered angles intercepting the same arc of circle have the same measure (Figure 1).

There are two versions of these theorems, one concerning the geometric angles and the other the oriented angles.

Geometric angles version [ modifier | Modifier and code ]

Theorem [ 2 ] – Let m be a point of a circle γ, from Center O, A and B are two points of the distinct circle of M. If the Amb and Aob angles intercept the same Arc AB then:

2 AMB^= AOB^{Displaysyle 2 {Widehat {with}} = {widehat {aob}}
after-content-x4

.

There are therefore two situations, one where the inscribed angle of the summit M is acute, so the angle in the center of the top O salient (Figure 1), the other where the inscribed angle of summit m is obtuse, therefore the angle in the center of the top O Returning (Figure 2).

Particular case [ modifier | Modifier and code ]

The case of an angle inscribed in a semicircle is the particular case for which the angle in the center is a flat angle, and therefore the inscribed angle is a right angle.

Version relating to oriented angles [ modifier | Modifier and code ]

The statement and demonstration of the property are much simpler with oriented angles.

Theorem [ 3 ] – Be A , B And M three distinct points, and γ a center circle O Going through A And B . Point M belongs to γ ​​if and only if:

( OA→, OB→) ≡ 2 ( MA→, MB→) against 2 Pi {displaystyle ({overrightarrow {OA}},{overrightarrow {OB}})equiv 2({overrightarrow {MA}},{overrightarrow {MB}})mod {2pi }}

.

after-content-x4

Geometric angles version [ modifier | Modifier and code ]

Angle inscrit 3.svg

The blue and green angles intercept the same arc (pink); they even measure th . The brown angle intercepts the black arc, which completes the pink arc; It is additional to the other two angles.

Corollary – Two angles inscribed in a circle and intercepting the same arc are of the same measure.

This property is an immediate consequence [ 2 ] From the theorem of the angle to the center above.

Complement – Two angles inscribed in a circle intercepting complementary circle arches [ 4 ] are additional.

The registered angles intercept two complementary arches if their summits are on both sides of the rope associated with the two arcs.

The property set out is still a direct consequence of the theorem of the angle in the center. When the arcs are complementary, the sum of the angles in the center gives a full angle. As the registered angles are worth half of the angles in the center, the sum of the registered angles gives a flat angle.

Applications [ modifier | Modifier and code ]

This theorem is the basis of the notion of focus circle, or Rowland circle, in spectrometry.

Angle of the rope and a tangent [ modifier | Modifier and code ]

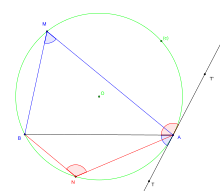
Angle corde tangente.svg

The property of the inscribed angles becomes widespread in the corners that the rope underlies the arc with a tangent:

The inscribed angle is even measured as the angle formed by the rope, which joins the ends of the arc, with the part of the tangent to the circle at one end of the rope, located opposite the ‘Angle in question in relation to the rope.

The inscribed angle

AMB^{Displaysyle {Widehat {with}}}

To even measure as that of one of the two angles formed by the tangent (TT ‘) in the circle with the rope [AB]:

The inscribed angle

AMB^{Displaysyle {Widehat {with}}}

is the same as the angle

BAT^{displaystyle {widehat {BAT}}}

of the rope [BA] with the tangent [at).

BAT^{displaystyle {widehat {BAT}}}

is the limit position of the inscribed angle

BMA^{displaystyle {widehat {BMA}}}

When M “tends” to A.

Version relating to oriented angles [ modifier | Modifier and code ]

For oriented angles, property becomes a characterization of the circle passing through the points A , M And B .

Theorem – And

C {displaystyle Gamma }

is the circle circumscribed to a non -flat triangle With So for any point N distinct from A And B , on a

It will be noted that equality is only true, which explains why the geometric angles can be additional.

Cordes secantes angle.png

Application to the corner between two senior strings [ modifier | Modifier and code ]

Theorem of the angle between two senior strings : the angle between two senior strings is equal to the average of the angles in the intercepted center; With the notations of the figure:

AMB′^= A′MB^= first 2 ( AOB′^+ A′OB^) {Displaysyle {widehat {with ‘}} = {widehat {a’mb}} = {FRAN {1} {2}} ({widehat {aob’}}+{widehat {a’OB}}}}

.

Demonstration :

According to the registered angle theorem,

A′AB^= A′B′B^= a {displaystyle {widehat {A’AB}}={widehat {A’B’B}}=alpha }

And

AA′B′^= ABB′^= b {displaystyle {widehat {AA’B’}}={widehat {ABB’}}=beta }

, and according to the property of the angles of the triangle

A M A ′ {displaystyle AMA’}

(or

B M B ′ {displaystyle BMB’}

),

AMB′^= a + b {Displaysyle {Widehat {with ‘}} = alpha +beta}

 ; or

a = first 2 A′OB^{displaystyle alpha ={frac {1}{2}}{widehat {A’OB}}}

And

b = first 2 AOB′^{displaystyle beta ={frac {1}{2}}{widehat {AOB’}}}

Hence the result.

We deduce that if the strings are perpendicular, we have the relationship between arc lengths:

AA′⌢ + BB′⌢ = A′B⌢ + B′A⌢ = Pi R {Displaystyle {overlooked {frown} {aa ‘}}+{overlooked {frown} {bb’}} = {overlooked {frown} {a’b}}+{overlooked {frown} {b’a}} = pi r }

, known relationship of Archimedes [ 5 ] .

  1. ↑ An inscribed angle is an angle whose summit belongs to the circle. Thus, on the diagram, the AMO angle is registered in the circle because M is placed on the circumference.
  2. ↑ a et b For a demonstration, see for example the chapter ” Inscribed angle and angle in the center “The lesson” theorem of the inscribed angle “on Wikivers.
  3. ↑ For a demonstration, see for example the chapter “version relating to the oriented angles” of the lesson “theorem of the inscribed angle” on Wikivers.
  4. ↑ One of the arcs, supplemented by the other, forms the whole circle. See complementary (sets of sets).
  5. ↑ David wells, The Penguin Dictionary of Geometric Curiosities , Eyrolles, , p. 107

On other Wikimedia projects:

after-content-x4