Derivation of Kepler’s laws

The Read of Kepler which describe the properties of the orbits of objects subjected to the gravitational force generated by a massive body can be theoretically deduced by applying the principles of dynamics (Newton equations).

In the procedure exposed, the existence of a full first of the motorcycle will initially demonstrate, the areolar speed (second law of Kepler); Subsequently it will be proven that the trajectories in the space of the coordinates of the system are elliptical (first law) and finally the dependence of the orbit period will be found on the length of the greater semiase of the ellipse (third law).

For the derivation of Kepler’s laws starting from Newtonian equations and universal gravitation law, it is first of all to introduce approximation.

We will limit ourselves to the case in which the mass of the planet is negligible compared to that of the sun; In this case we can fix the center of the reference system in the center of the sun and neglect the motion.

In this approximation, Kepler’s problem is reduced to that of a motorcycle in the central field in which Newton’s equation is worth

${DISPLASYSTLE M {dot}} =-{frac {partial v} {partial r}}}$

Where

${displaystyle V(r)=-k/r}$

This report is obtained by integrating on

${displaystyle r}$

the expression of the gravitational force

${displaystyle F(r)=-k/r^{2}}$

.

The second law: from the conservation of the angular moment to that of areolar speed [ change | Modifica Wikitesto ]

Kepler’s second law says that areolar speed is constant during the motion.

Now, introducing a polar coordinate system

${displaystyle (r,theta )}$

, with their respective versors

${displaystyle (mathbf {hat {r}} ,mathbf {hat {theta }} )}$

you have, trivially

${displaystyle mathbf {r} =rmathbf {hat {r}} }$

.

By deriving this quantity with respect to time, it is obtained (by applying the product derivation rule and remembering

${Displaystyle Mathbf {Dot {R}}} ={Dot {theta }} Mathbf {hat {theta } } }$

,

${Displaystyle Mathbf {Dot {HAT {Theta }}}} =-{Dot {theta }}mathbf {r} }$

${Displaystyle Mathbf {Dot {R}} ={Dot {R}} Mathbf {R} +R {Dot {theta } }mathbf {hat {theta } } }$

Now, considering the unitary mass for simplicity, the angular moment

${displaystyle mathbf {L} }$

Vale (exploiting the properties of the vector product):

${Displaystyle Mathbf {L} =Mathbf {R} Times Mathbf {R}} =Mathbf {R} TIMES {R} {R} {R} {R} Mathbf {R} +Mathbf {R} TIMES R {DOT {THETA } }mathbf {hat {theta }} =r{dot {theta }}(mathbf {r} times mathbf {hat {theta } )=r^{2}{dot {theta }}(mathbf {hat {r}} Times Mathbf {hat {theta } )=r^{2}{dot {theta }}}$

Ortogonally directed to the plan in which the motorcycle takes place.

For the law of conservation of the angular moment, it follows that the quantity

${displaystyle r^{2}{dot {theta }}}$

It is an integral of the motion.

Considering the areolar speed

${displaystyle C}$

As a temporal derivative of the area swept by the vector radius, you have

${displaystyle mathrm {d} S={frac {1}{2}}r^{2}{dot {theta }}mathrm {d} t}$

In fact, considering a corner

${displaystyle mathrm {d} theta ={dot {theta }}mathrm {d} t}$

, the area swept in the infinite temporal interval, the area element is given by the middle of the square of

${displaystyle r}$

for the corner in the center.

Performing the derivative:

${displaystyle C={frac {mathrm {d} S}{mathrm {d} t}}={frac {1}{2}}r^{2}{dot {theta }}={frac {1}{2}}L}$

.

Therefore the areolar speed is an integral of the motion. ^[first]

It can be seen how the validity of the second law is completely independent of the expression of the potential considered, it is in fact a property of all the potential central.

The first law: the elliptical trajectory of the planets [ change | Modifica Wikitesto ]

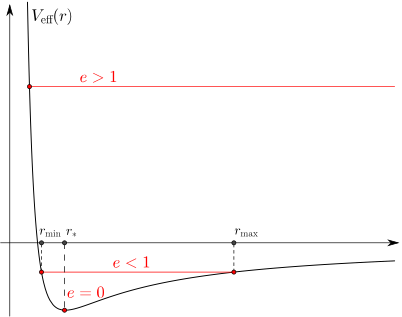
First of all, the two -dimensional problem of motion in the central field can be easily reduced to a unidimensional case using the definition of effective potential.

The equations of the motorcycles, in fact, can be rewritten considering the form

${displaystyle V_{text{eff}}={frac {L^{2}}{2r^{2}}}+V(r)={frac {L^{2}}{2r^{2}}} -{frac {k} {r}}}$

In a motorcycle in the central field, the relationship between the corner

${displaystyle theta }$

and the distance from the origin

${displaystyle r}$

is given by the integral

${displaystyle theta =int {frac {L/r^{2},mathrm {d} r}{sqrt {2(E-V_{text{eff}}(r))}}}=int {frac {L/r^{2},mathrm {d} r}{sqrt {2(E-V_{text{eff}}(r))}}}=arccos {frac {L/r-k/L}{sqrt {(2E+k^{2}/L^{2})}}}}$

where the supplementary constant was placed equal to zero. This means that the integral is calculated starting from the pericenter of the orbit.

Now defining the quantities

${displaystyle p=L^{2}/k,qquad e={sqrt {1+2EL^{2}/k^{2}}}}$

and properly reversing the expression of

${displaystyle theta }$

you reach the equation

${Displaystyle r = {fraud {p} {1+echoes theta}}}$

.

This other is only the expression of any conical in polar coordinates centered in a fire.

With

${displaystyle e<1,}$

This represents an ellipse with eccentricity

${displaystyle e}$

and semilate right

${displaystyle p}$

.

In particular, it is possible to obtain the values ​​of the semiassi

${displaystyle a}$

It is

${displaystyle b}$

:

${displaystyle a={frac {p}{1-e^{2}}}={frac {L^{2}/k}{1-1-2EL^{2}/k^{2}}}={frac {k}{2|E|}}}$

${displaystyle b={frac {p}{sqrt {1-e^{2}}}}={frac {L^{2}/k}{sqrt {1-1-2EL^{2}/k^{2}}}}={frac {L}{sqrt {2|E|}}}}$

The third law: Period-SEAMIA DEPTENCE MAGGIORE [ change | Modifica Wikitesto ]

In the expressions of

${displaystyle a}$

It is

${displaystyle b}$

As soon as you get, you can see how the major semiase

${displaystyle a}$

Both dependent only on the total energy of the system, while the minor semiase is also the function of the angular moment. Since the rotation period, in the motorcycle in the central field, is the function of the energy only, this fact allows to infer a relationship for the period only concerning the greater semiase of the ellipse.

In particular, they will have (being

${displaystyle pi ab}$

the area of ​​the ellipse e

${displaystyle C}$

the areolar speed, whose value is constant and equal to

${displaystyle L/2}$

).

${displaystemyle t (e) = {frac {c {c} {c {} | {c {sqrrt {quirc {sqrnt {vac} {sqrt {c {sqrnt {c {sq {frac} {{frac}} {frac}} {frac}} {frac}} {frac} {{frac} } {L}} = pi k {sqrt {2}} | e | ^ – 3/2}}$

Now, recovering the expression of

${displaystyle a}$

depending on the energy you have

${displaystyle |E|={frac {k}{2a}}}$

, replacing this value in the previous equation is obtained

${displaystyle T(E)=pi k{sqrt {2}}left({frac {2a}{k}}right)^{3/2}}$

from which it is deduced that

${Displaystyle t ^ {2} ^ {3}}$

As Kepler’s third law says. ^[first]