Dreieck – Wikipedia

Posted on April 2, 2022 by lordneo

before-content-x4

UN Triangle (Également obsolète Triangle , Latin: triangulum) est un polygone et une figure géométrique. C’est le chiffre le plus simple du niveau, qui est limité par les lignes droites. Ses limites sont appelées pages . À l’intérieur, il y a trois angles, les angles intérieurs so-appels. La récolte de cet angle est appelée Pierres angulaires du triangle. Une généralisation du terme de triangle sur les géométries non taxes est également possible. Dans ce cas, les limites doivent être des géodes.

after-content-x4

En trigonométrie, une sous-zone de mathématiques, les triangles jouent le rôle essentiel. Voir en particulier la géométrie triangulaire.

Division

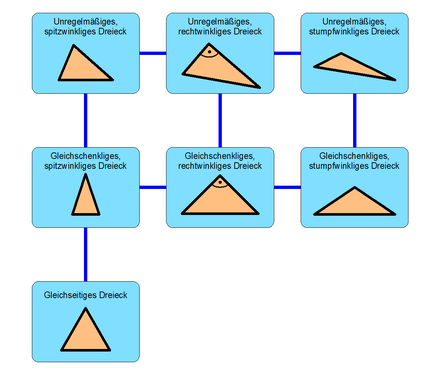
Par des longueurs latérales

Coins

Les triangles bien rangés et brumeux sont également sous le nom Triangle suisse résumé.

Le triangle général

Définition et propriétés

La somme des angles intérieurs dans un triangle plat est toujours 180 °.

Un triangle est défini par trois points qui ne sont pas en ligne droite. vous serez Coins appelé le triangle. Les voies de connexion entre deux coins sont appelées pages du triangle. Le triangle divise le niveau en deux zones, le Extérieur et le Intérieur du triangle. L’angle, qui est formé par deux pages formées à un point d’angle, est une taille importante pour caractériser le triangle.

En géométrie, les pierres angulaires du triangle sont généralement avec

after-content-x4

{displaystyle a}

$A$ ,

{displaystyle b}

$B$ et

{DisplayStyle C}

$C$ Décrit, généralement comme indiqué, dans le sens horaire. La page qui est en face d’un coin devient analogue

{displaystyle a}

$a$ ,

{displaystyle b}

$b$ ou.

{DisplayStyle C}

$c$ appelé. Cela réside z. B. Le côté

{displaystyle a}

$a$ Le point d’angle

{displaystyle a}

$A$ opposé, alors connectez les points

{displaystyle b}

$B$ et

{DisplayStyle C}

$C$ . Souvent avec

{displaystyle a}

$a$ ,

{displaystyle b}

$b$ et

{DisplayStyle C}

$c$ aussi la longueur de la page respective à la place

{DisplayStyle BC}

$BC$ ,

{displaystyle ca}

$CA$ ou

{displaystyle ab}

$AB$ désigné.
Les angles deviennent

{displaystyle alpha}

$alpha$ ,

{DisplayStyle Beta}

$beta$ et

{DisplayStyle Gamma}

$gamma$ appelé.

{displaystyle alpha}

$alpha$ Est l’angle au point d’angle

{displaystyle a}

$A$ ,

{DisplayStyle Beta}

$beta$ Est au point d’angle

{displaystyle b}

$B$ et

{DisplayStyle Gamma}

$gamma$ Est au point d’angle

{DisplayStyle C}

$C$

La somme des angles intérieurs dans un triangle planaire (niveau) est toujours à 180 °.
La somme des angles extérieurs est à 360 °. Seul un angle extérieur est inclus dans la somme pour chaque point d’angle. Étant donné que les deux angles externes d’un point d’angle sont un angle de sommet, ce sont toujours de la même taille. La somme aller L’angle extérieur est donc à proprement parler, 2 · 360 ° = 720 °.
La longueur totale des deux côtés d’un triangle est au moins aussi grande que la longueur du troisième côté. Ces relations peuvent être exprimées dans le soulagement triangulaire SO.

Ces propriétés intuitivement perspicaces des triangles de niveau découlent des axiomes de la géométrie euclidienne.

Calcul de tout triangle

Aperçu des voies informatiques et des outils à utiliser lors du calcul de tout triangle

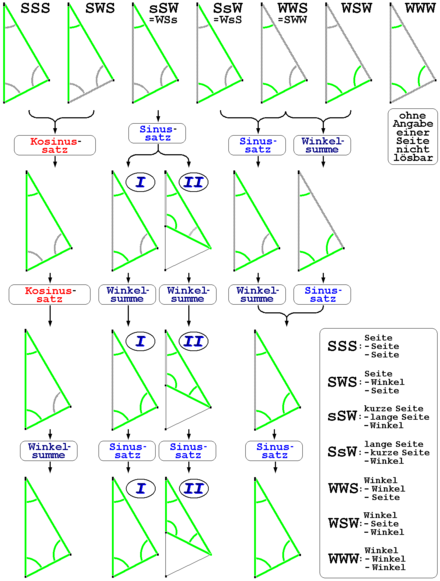
Un triangle a trois côtés et trois angles intérieurs. S’il y a trois informations sur la taille de ces pages ou angles, les autres pages ou angles manquants peuvent être calculés à partir de celui-ci, à moins que seuls les trois angles soient donnés.

Selon la combinaison de pages et / ou d’angles bien connues, le résultat en est un ou ambigu (voir Fig.).

De cette façon, les taux de congruence fournissent initialement trois constellations qui sont toujours clairement résolubles, qui sont symboliquement impliquées SSS , Sws et WSW mentionné, par lequel S Pour une page connue et DANS représente un angle connu.

Cas SSW ou WSS

Le Cas SSW ou WSS En revanche, il est clair que si l’angle bien connu du plus grand des deux pages données opposées (cas SSW) – Si elle se trouve le plus petit PAGE OPPOSÉE (cas SSW), il y a généralement deux triangles différents qui remplissent les conditions de départ. Cependant, cela ne doit pas toujours être le même que le cas spécial le montre avec le rapport d’aspect 1: 2 et l’angle de 30 °, dans lequel il n’y a qu’un tel triangle si l’angle opposé à l’angle plus long Page 90 °. Après tout, la situation purement arithmétique doit être mentionnée qu’aucun triangle ne remplit les conditions de départ, à savoir lorsque le sinus du plus long Les angles opposés côté donnent une valeur> 1 (dans le cas de vrais triangles, cependant, cela est naturellement exclu).

WWS ou cas SWW

Le WWS ou cas SWW peut être résolu de deux manières (comme on peut le voir sur l’illustration adjacente): soit vous calculez l’une des deux pages manquantes à l’aide de l’ensemble de sinus, puis continuez à calculer comme dans SSW , ou vous déterminez ce qui est beaucoup plus pratique au moyen de la quantité angulaire dans le triangle le troisième coin manquant, puis continue comme dans WSW-Fall .

Chuter SSS

Si le plus grand des trois côtés est plus petit que la somme des deux autres côtés, le triangle (à l’exception de la congruence) est clairement déterminé. Sinon, il n’y a pas de triangle avec les trois côtés spécifiés. Les angles intérieurs du triangle peuvent être z. B. Calculez avec l’ensemble de cosinus.

Www-chute

Le Www-chute Si les triangles ne sont pas clairement résolubles, car en réalité, il n’y a que deux informations indépendantes, en revanche, la taille du troisième angle résulte inévitablement toujours de la taille des deux autres. Sans une page donnée est le Former du triangle que vous recherchez, son Taille Mais reste indéfini.

Sinus et phrase cosinus

Les outils les plus importants pour le calcul de tout triangle s’ajoutent à l’angle de l’angle dans le triangle de l’ensemble des sinus et des cosinus, qui ne jouent qu’un rôle subordonné par rapport aux autres taux triangulaires tels que le taux de projection et le taux de danse ainsi que les taux d’angle à moitié.

Le plus intentionnel, mais aussi le plus puissant des trois outils, est l’ensemble de cosinus, car il est le seul pour un triangle sans toutes les informations d’angle un premier angle (puis aider avec l’ensemble de sinus plus simple et l’angle des angles dans le triangle). Par conséquent SSS ou Sws , tandis que tout le reste est fait plus facilement et plus rapidement par sinus et angle.

Comme on peut le voir ci-dessous, l’ensemble de cosinus commence ainsi que la phrase des Pythagore, et en fait vous pouvez le comprendre comme un cas particulier de l’ensemble du cosinus:

{displayStyle a ^ {2} = b ^ {2} + c ^ {2} -2cdot bcdot ccdot cos (alpha),}

{displayStyle b ^ {2} = a ^ {2} + c ^ {2} -2cdot acdot ccdot cos (bêta),}

{displayStyle c ^ {2} = a ^ {2} + b ^ {2} -2cdot acdot bcdot cos (gamma).}

Si l’angle, qui est enfermé par deux pages d’un triangle, devient un droit à droite, son cosinus devient nul et ce qui reste de l’ensemble de cosinus pertinent n’est rien de plus qu’une autre version du “Pythagore”.

Vous ne connaissez que ses trois côtés d’un triangle

{displaystyle a}

$a$ ,

{displaystyle b}

$b$ et

{DisplayStyle C}

$c$ , ses angles intérieurs peuvent être déterminés comme suit à l’aide de la fonction d’arcuscosine (ARCCOS):

{displayStyle {begin {aligned} cos (alpha) & = {frac {b ^ {2} + c ^ {2} -a ^ {2}} {2cdot bcdot c}} \ alpha & = arccos Left ({frac {b ^ {2} + c ^ {2} -a ^ {2}} }} à droite), fin {aligné}}}

{displayStyle {begin {aligned} cos (beta) & = {frac {a ^ {2} + c ^ {2} -b ^ {2}} {2cdot acdot c}} \ beta & = arccos Left ({frac {a ^ {2} + c ^ {2} -b ^ {2}} à droite), fin {aligné}}}

{displayStyle {begin {aligned} cos (gamma) & = {frac {a ^ {2} + b ^ {2} -c ^ {2}} {2cdot acdot b}} \ gamma & = arccos Left ({frac {a ^ {2} + b ^ {2} -c ^ {2}} } à droite) .end {aligné}}}

L’ensemble de sinus est disponible en trois variantes qui peuvent être résumées comme suit:

{displayStyle {frac {a} {sin (alpha)}} = {frac {b} {sin (beta)}} = {frac {c} {sin (gamma)}} = 2cdot r}

Comme on peut le voir, l’ensemble des sinus est beaucoup plus simple: si vous connaissez l’une des trois pauses, vous connaissez automatiquement tous les autres. Cependant, au moins l’un des trois angles intérieurs doit toujours être connu ici et, sinon, sont d’abord utilisés à la phrase en cosinus (voir ci-dessus).

Formules

Excellents cercles, droits et points

• Point de circuit DANS (vert) au moyen des deux-sensibilités du milieu OU et Mu
• Point central du cercle je (rouge) au moyen des deux angles Dans _bet Dans _c
• l’accent principal S (bleu foncé) au moyen des deux côtés mi-temps Pour et CO
• élévation H _un, H _bet H _cAvec un point de coupe de hauteur H (Hellbraun)
• District de Feuerbach au centre F (bleu clair) par le 9 Intersection O , D , ET , g , J , K , L , M et N
• Euler-Straight C’est (rouge) à travers les points DANS , S , F et H

Triangle avec ses coins, ses côtés et ses angles ainsi que la zone environnante, le circuit et une partie d’un cercle sous la forme habituelle étiquetée

Chaque triangle a un rayon, c’est-à-dire un cercle qui traverse ses trois points d’angle. Le centre du rayon est l’intersection des trois crises moyennes-métal. Ce sont les cades de loterie à travers les points centraux des côtés.

Les angulaires des trois angles intérieurs ont également coupé un point commun, à savoir au centre du district. Cela touche les trois côtés de l’intérieur. Les trois cercles, chacun touchent un côté de l’extérieur et les extensions des deux autres côtés, sont appelées groupes du triangle.

L’objectif d’un triangle est l’intersection commune des trois demi-fins latérales, c’est-à-dire les voies de connexion respectives des pierres angulaires au centre du côté opposé. L’objectif est divisé en côté du côté dans un rapport de 2: 1. Exemple de l’image:

{DisplayStyle {overline {cs}}: {overline {so}} = {overline {as}}: {overline {sj}} = 2: 1}

${displaystyle {overline {CS}}:{overline {SO}}={overline {AS}}:{overline {SJ}}=2:1}$ .

Les trois hauteurs, c’est-à-dire les lots des points d’angle du côté opposé, ont également coupé sur un point commun, le point de coupe de hauteur. Avec l’aide des hauteurs, la zone d’un triangle peut être calculée (voir zone triangulaire).

Un autre cercle bien connu sur le triangle est le district de Feuerbach. Il le fera aussi Neuf points Appelé, car il traverse les trois points du centre latéral, les trois points de pied des hauteurs et les trois focus des sections supérieures de la hauteur. Son objectif est comme la focalisation, le centre de la zone et le point de coupure de hauteur sur l’eulerserer.

Triangles spéciaux

Triangles équilatéraux

Un triangle équilatéral.
Ça s’applique:

{displayStyle a = b = c}

Caractéristiques

Un triangle dans lequel les trois côtés sont les mêmes longs est appelé le triangle équilatéral. Les trois angles intérieurs sont de la même taille et sont donc 60 ° (c’est donc un triangle à angle pointu). Cela signifie que les triangles équilatéraux sont des polygones réguliers.

Tous les triangles d’équilibre sont similaires les uns aux autres et congruents précisément lorsque leurs longueurs latérales sont les mêmes. Moyenne, côté du côté et de la hauteur d’un côté ainsi que l’angle de l’angle de l’angle opposé, tombe ensemble en cas de triangle équilatéral. Il en va de même pour le centre de la zone, le centre du circuit, la focalisation et le point de coupe de hauteur du triangle équilatéral, de sorte que ce point est souvent facile Se concentrer est appelé.

Formules

Pour un triangle équilatéral avec la longueur latérale

{displaystyle a}

$a$ est applicable:

Preuve Voir les liens Web ci-dessous.

Triangles de blanchisse

Selon une vue moderne, un triangle égal est un triangle dans lequel au moins Deux pages ont la même longueur. Ces pages sont comme jambe Décrit, la troisième page est appelée Base du triangle équivalent. Les deux angles à la base ( Boutique de base ) sont identiques. Le point où les deux jambe rencontrer, volonté Haut appelé, l’angle là-bas Angle en haut .

Un triangle linéaire est une règle sous la forme d’un triangle équivalent angoissé à droite.

Dans un triangle équivalent, les crimes moyens-métaux de la base, le côté de la base et la hauteur sur la base ainsi que l’angle de l’angle de l’angle de pic tombent ensemble. Vous pouvez faire la longueur de cette route, en particulier la hauteur

{displayStyle h_ {c}}

$h_{c}$ Déterminez en utilisant la phrase Pythagore à la moitié du triangle. Il en résulte

{displayStyle h_ {c} = {sqrt {a ^ {2} – {tfrac {c ^ {2}} {4}}}}}

$h_{c}={sqrt {a^{2}-{tfrac {c^{2}}{4}}}}$ .

Triangles à droite

Un triangle à angle droit est un triangle qui a un angle de 90 °, c’est-à-dire un angle droit. Le côté opposé à l’angle droit est le côté le plus long du triangle et est Hypoténuse appelé. Les deux autres côtés sont appelés Kathenen . En termes de l’un des angles pointus du triangle Détente et la catte en face de l’angle comme Contraire .

Les longueurs des trois côtés d’un triangle angoissé droit sont liées à la phrase du pythagore: le carré de la longueur de l’hypoténuse (dans le graphique comme

{DisplayStyle C}

$c$ Décrit) est égal à la somme des carrés des longueurs des cathets (

{displaystyle a}

$a$ et

{displaystyle b}

$b$ ). Inversement, un triangle dans lequel le côté se longueur dans la relation

{displaystyle a ^ {2} + b ^ {2} = c ^ {2}}

$a^{2}+b^{2}=c^{2}$ Tenez-vous ensemble, un triangle à droite avec de l’hypoténuse

{DisplayStyle C}

$c$ .

La hauteur

{displayStyle h = h_ {c}}

$h=h_{c}$ Un triangle angoissé droit divise l’hypoténuse en deux parties

{displaystyle p}

$p$ et

{displayStyle Q}

$q$ , donc les deux triangles partiels avec les côtés

{displaystyle p}

$p$ ,

{displaystyle a}

$a$ ,

{displaystyle h}

$h$ et

{displayStyle Q}

$q$ ,

{displaystyle h}

$h$ ,

{displaystyle b}

$b$ sont à nouveau corrects. Si vous connaissez deux des six informations (

{displaystyle a}

$a$ ,

{displaystyle b}

$b$ ,

{DisplayStyle C}

$c$ ,

{displaystyle p}

$p$ ,

{displayStyle Q}

$q$ et

{displaystyle h}

$h$ ) Les quatre autres valeurs manquantes peuvent être calculées à partir des formules répertoriées dans le tableau suivant.

Fonctions d’angle dans le triangle angoissé à droite

Le rapport entre les cathets et l’hypoténuse peut également être clairement déterminé par les deux angles pointus du triangle angoissé droit. Les six fonctions suivantes seront Fonctions d’angle Ou appelé fonctions trigonométriques.

Les éléments suivants peuvent être présentés à partir de ce qui précède par formation de balayage.

fonction	calcul
Le Kotangens est la relation entre le cathétique ancatré et opposé, c’est-à-dire la valeur de balayage du Tang.	${displayStyle cot (alpha) = {frac {b} {a}} = {frac {1} {tan (alpha)}}}$
Le SEK est le rapport de l’hypoténuse à l’Ancatheton, c’est-à-dire la réciprocité du cosinus.	${displayStyle sec (alpha) = {frac {c} {b}} = {frac {1} {cos (alpha)}}}$
Le Kostekans est la relation de l’hypoténuse avec le cathétique opposé, c’est-à-dire la réciprocité du sinus.	${displayStyle csc (alpha) = {frac {c} {a}} = {frac {1} {sin (alpha)}}}$

Les fonctions d’inversion des fonctions d’angle mentionnées sont appelées Arkussinus, Arkuskosinus, Arkustangens, etc. – Leur application principale est en conséquence de fournir les angles associés aux valeurs sinus, cosinus ou tangibles.

Triangles irréguliers

Un triangle est appelé irrégulièrement qui remplit ces deux conditions:

Les trois côtés sont différents.
Les trois angles sont de taille différente.

Si l’une des deux conditions est remplie, l’autre est automatiquement remplie.

Égalité spéciale de l’espace

If you replace the right-angled triangle in the Pythagoras figure with any triangle, you get the so-called Vecten figure, named after the French mathematician Vecten, who was in France from 1810 to 1816 at the Lycée de Nîmes and a total of 22 articles about this figure in the specialist magazine Annal Joseph Diaz Gargonne (1771 –1859) published ( Figure 1 ). ^[2]^[3]

Si vous combinez les pierres angulaires voisines des carrés dans la figure de vecten, trois autres triangles de flancs soient créés avec la propriété que les quatre triangles (bleu, vert, jaune et rouge) sont les mêmes (la même zone ( Figure 2 ).

Les preuves résultent des chiffres présentés. Deux angles chacun avec des arcs de la même couleur complètent 180 °. Si vous tournez le triangle des trois flancs autour du point d’angle associé du triangle intérieur de 90 ° dans le sens des aiguilles d’une montre ( figure 3 ), C’est ainsi qu’un concave est composé de quatre triangles composés Figure 4 ). Depuis le couple triangulaire

{displayStyle ABC / BEC}

${displaystyle ABC/BEC}$ ,

{displayStyle ABC / ACF}

${displaystyle ABC/ACF}$ et

{displayStyle ABC / DBA}

${displaystyle ABC/DBA}$ Dans chaque cas, dans la longueur d’un côté et de la longueur de la hauteur qui y est construite, les quatre triangles sont les mêmes. ^[4]^[5]

Triangles de géométrie non tax

Triangles sphériques

Les triangles sur une balle, dont les trois côtés font partie de grands cercles, sont appelés triangles sphériques ou triangles de balle. Leurs longueurs latérales ne sont pas spécifiées dans la dimension d’une longueur (mètres, centimètres ou similaires), mais comme un angle associé au centre de la balle.

Un triangle sphérique a une quantité d’angle supérieure à 180 °. L’excès est appelé excès sphérique et surtout dans des formules

{displayStyle Varsilon}

$varepsilon$ désigné:

{DisplayStyle alpha + bêta + gamma = 180 ^ {circ} + varepsilon}

L’excès maximal de 360 ° se produit avec un «triangle» avec trois angles étirés à 180 °. Ce triangle dégénéré en un grand cercle a l’angle de l’angle 3 · 180 ° = 540 ° et

{displayStyle Varsilon = 540 ^ {circ} -180 ^ {circ} = 360 ^ {circ}}

${displaystyle varepsilon =540^{circ }-180^{circ }=360^{circ }}$ .

L’excédent se bloque directement avec la zone

{displaystyle f}

$F$ du triangle ensemble:

{displayStyle Varsilon = {frac {f} {r ^ {2}}}}

par lequel

{displaystyle r}

$R$ le rayon sphérique et

{displaystyle pi}

$pi$ Le nombre de circuits signifie.

Les triangles sphériques peuvent être calculés de manière analogue aux triangles de niveau, pour lesquels il est en géodésie. B. L’ensemble des sinus sphériques, la phrase en cosinus, le taux de projection et divers taux de demi-angle – voir la trigonométrie sphérique.

Triangles hyperboliques

Géométrie non taxe – dans laquelle l’axiome parallèle ne s’applique pas – comprend également des triangles sur une zone de selle. Alors qu’une balle est courbée partout, la selle et d’autres zones hyperboliques ont à la fois une courbure convexe et concave (leur produit, la taille de courbure négatif ).

En conséquence, l’excès est négatif – d. H. L’angle de l’angle d’un triangle est sur une zone de selle plus petit de 180 °. Les ensembles de congruence font des déclarations sur les tailles triangulaires (longueur latérale, angle) qui sont nécessaires pour déterminer clairement un triangle.

Phrases autour du triangle

Triangle comme symbole

Le triangle est utilisé comme symbole, par exemple en théologie, comme symbole idéologique, comme symbole mathématique et aussi dans les signes.

Voir également

littérature

Liens web

Individuellement

↑ Victor Oxman: Sur l’existence de triangles avec des longueurs données d’un côté et deux bissecteurs d’angle adjacents. Forum Geometricorum 4, 2004, S. 215 , consulté le 14 juin 2022 .
↑ Claudi Alsina, Roger B. Nelsen: Perles de mathématiques – 20 figures géométriques comme points de départ pour les voyages d’exploration mathématique , Springer Spektrum, Springer-Verlag GmbH Berlin 2015, ISBN 978-3-662-45460-2, S. 4–7
↑ Jean-Louis Ayme: Vecten figure Article PDF de Jean-Louis Ayme de son site Web , consulté le 24 février 2023
↑ Roger B. Nelsen: Preuve sans mots , Édition en langue allemande édité par Nicola Oswald, Springer Spektrum, Springer-Verlag Berlin Heidelberg 2016, ISBN 978-3-662-50330-0, page 22
↑ Snover, S. L.: Quatre triangles avec une surface égale. Dans: Nelsen, R.: Épreuves sans paroles II. Mathématique, Association of America, Washington, S. 15 (2000)

after-content-x4

Dreieck – Wikipedia

Division

Par des longueurs latérales

Coins

Le triangle général

Définition et propriétés

Calcul de tout triangle

Cas SSW ou WSS

WWS ou cas SWW

Chuter SSS

Www-chute

Sinus et phrase cosinus

Formules

Excellents cercles, droits et points

Triangles spéciaux

Triangles équilatéraux

Caractéristiques

Formules

Triangles de blanchisse

Triangles à droite

Fonctions d’angle dans le triangle angoissé à droite

Triangles irréguliers

Égalité spéciale de l’espace

Triangles de géométrie non tax

Triangles sphériques

Triangles hyperboliques

Phrases autour du triangle

Triangle comme symbole

Voir également

littérature

Liens web

Individuellement

Recent Posts

Recent Comments

Archives

Categories

Meta