K-means-algorithmus – wikipedia

UN k -Means-algorithmus est un processus de quantification vectorielle qui est également utilisé pour l’analyse en grappes. Un grand nombre d’objets similaires deviennent un nombre auparavant connu de k Groupes formés. L’algorithme est l’une des techniques les plus fréquemment utilisées pour regrouper des objets car elle trouve rapidement les centres des grappes. L’algorithme préfère les groupes avec une faible variance et une taille similaire.

L’algorithme présente de solides similitudes avec l’algorithme du championnat d’Europe et se caractérise par sa simplicité. ^[d’abord] Les extensions sont k-meian-algorithmus et le K-means ++ algorithmus .

Le terme “k-means” a été utilisé pour la première fois par MacQueen en 1967, ^[2] Cependant, l’idée revient à Hugo Steinhaus en 1957. ^[3] L’algorithme standard, qui est surtout connu comme “l’algorithme K-Means” aujourd’hui, a été proposé par Lloyd pour la modulation du code d’impulsion en 1957, mais publié uniquement dans un magazine informatique en 1982 ^[4] Et coïncide en grande partie avec la méthode Forgy, qui a été publiée en 1965. ^[5] Une autre variante est celle de Hartigan et Wong, qui évite les calculs de distance inutiles en utilisant également la distance jusqu’à la deuxième nuit. ^{[6] [7]} Une affectation précise des algorithmes est souvent faite: en particulier, l’algorithme de Lloyd / Forgy est souvent décrit, mais MacQueen est mentionné comme la source.

Le but de k -Means consiste à faire l’enregistrement des données de cette manière

${displaystyle k}$

Les partitions pour partager que la somme des écarts carrés par rapport au cluster se concentre est minime. Mathématiquement, cela correspond à l’optimisation de la fonction

${displayStyle j = sum _ {i = 1} ^ {k} sum _ {mathbf {x} _ {j} en s_ {i}} {| mathbf {x} _ {j} – {boldSymbol {mu}} _ {i} | ^ {2}}}$

Avec les points de données

${displayStyle mathbf {x} _ {j}}$

Et l’objectif

${displayStyle {boldsymbol {mu}} _ {i}}$

Le cluster

${displayStyle s_ {i}}$

.
Cette fonction cible est basée sur la méthode des plus petits carrés et on parle également de Clustering grâce à la minimisation de la variance , ^[8] Parce que la somme des variances du cluster est minimisée. Depuis aussi

${displayStyle | mathbf {x} _ {j} – {boldsymbol {mu}} _ {i} | ^ {2}}$

La distance euclidi carrée est commandée k -Mesans effectivement chaque objet au cluster le plus proche (selon la distance euclidieuse). Inversement, la moyenne arithmétique est un plus petit estimateur de carton, donc ce critère optimise également.

Étant donné que la recherche de la solution optimale est difficile (NP-SHW), un algorithme d’approximation est généralement utilisé comme l’heuristiken de Lloyd ou MacQueen. Depuis le problème de k Cela dépend de ce paramètre doit être déterminé par l’utilisateur. Cependant, il existe également des approches pour choisir ce paramètre en utilisant un deuxième objet (cf. x-means, critère d’information Akaike, critère d’information Bayesch et coefficient de silhouetting).

Algorithme lloyd [ Modifier | Modifier le texte source ]]

Le plus courant utilisé k -Lesseans algorithme est l’algorithme Lloyd, qui est souvent «le k -Means algorithme »est appelé, bien que Lloyd n’utilise pas ce nom. L’algorithme de Lloyd se compose de trois étapes:

1. Initialisation: Choisir
   ${displaystyle k}$

   valeurs moyennes aléatoires ( Moyens ):

   ${displayStyle Mathbf {m} _ {1} ^ {(1)}, ldots, mathbf {m} _ {k} ^ {(1)}}$

   De l’ensemble de données.

2. Mission: Chaque objet de données est attribué au cluster dans lequel la variance du cluster est la moins augmentée.
   
   ${displayStyle s_ {i} ^ {(t)} = gauche {mathbf {x} _ {j}: {big |} mathbf {x} _ {j} -mathbf {m} _ {i} ^ {(t)} {big |} ^ {2} leq {big |} Mathbf {m} _ {i ^ {*}} ^ {(t)} {Big |} ^ {2} {texte {für alle}} i ^ {*} = 1, ldots, kright}}$

   

3. Mettre à jour: Calculez les points centraux du cluster:
   
   ${affichestyle mathbf {m} _ {i} ^ {(t + 1)} = {frac {1} {| s_ {i} ^ {(t)} |}} sum _ {mathbf {x} _ {j} dans s_ {i} ^ {t)}}} Mathbf {x}$

   

Les étapes 2 à 3 sont répétées jusqu’à ce que les affectations ne changent plus.

L’algorithme de MacQueen [ Modifier | Modifier le texte source ]]

MacQueen a mené avec le terme ” k -Means ”Un autre algorithme:

1. Choisissez le premier
   ${displaystyle k}$

   Éléments comme centres de cluster

2. Way chaque nouvel élément vers le cluster dans lequel la variance augmente le moins et mettez à jour le centre de cluster

Bien qu’il soit à l’origine – probablement pas prévu, cet algorithme peut également être itéré afin d’obtenir un meilleur résultat.

Variations [ Modifier | Modifier le texte source ]]

• K-Means ++ essaie de trouver de meilleurs points de départ. ^[9]
• L’algorithme de filtrage utilise une arborescence K-D comme structure de données. ^[dix]
• L’algorithme K-Means peut être accéléré, en tenant compte de l’allégement triangulaire. ^[11]
• Bisecting k-means commence par
  ${displayStyle k = 2}$

  , puis divise toujours le plus grand cluster jusqu’à ce que vous souhaitiez k est atteint.

• X-Means commence par
  ${displayStyle k = 2}$

  et augmenté

  ${displaystyle k}$

  Jusqu’à ce qu’un critère secondaire (critère d’information Akaike ou critère d’information de Bayesche) ne s’améliore pas.

k -Means optimise les écarts carrés par rapport à une moyenne. Il ne peut donc être utilisé qu’avec des attributs numériques dans lesquels une moyenne sensée peut être calculée. Les attributs catégoriques (par exemple “” voiture “,” camion “,” vélo “) ne peuvent pas être utilisés, car aucune moyenne ne peut être calculée ici.

Le paramètre

${displaystyle k}$

Le nombre de clusters doit être connu à l’avance. Cependant, il peut également être déterminé expérimentalement. Le problème est que les différents clusters doivent être comparés et la fonction de coût avec l’augmentation

${displaystyle k}$

Monoton coule. Une solution est le coefficient de silhouette, l’un des

${displaystyle k}$

Fournit une évaluation indépendante des clusters. Il est non seulement vérifié à quel point un point de l’objectif de votre propre cluster est, mais les distances des autres zones de cluster sont également incluses dans l’évaluation du regroupement.

Les clusters dans l’enregistrement de données doivent être à peu près de la même taille, car l’algorithme varie toujours l’enregistrement de données au milieu entre deux centres de cluster.

L’enregistrement de données ne doit pas contenir beaucoup de bruit ou pas beaucoup de valeurs aberrantes. Des objets de données incorrects déplacent souvent considérablement les centres de cluster calculés et l’algorithme n’a pas de précautions contre de tels effets (cf. DBSCAN, qui prévoit explicitement des objets “bruit”).

k -Means est un algorithme puissant, mais non sans faiblesse. UN k -Leans Algorithme n’a pas à trouver la meilleure solution possible. La solution trouvée dépend fortement des points de départ sélectionnés. L’approche la plus simple consiste à démarrer l’algorithme plusieurs fois consécutif avec différentes valeurs de départ et à prendre la meilleure solution. Cependant, il existe également de nombreuses considérations sur la façon dont une distribution appropriée des valeurs de départ peut être obtenue. Entre autres choses, K-means ++ méritent d’être mentionnés, mais aussi avec la traction de petits échantillons, les centres de cluster peuvent être approximés avant le début des K-means. Cela fait également la différence que vous choisissiez des centres de cluster, ou que vous attribuez chaque point à un cluster, puis que vous déterminez les centres de cluster.

Un autre inconvénient est que le nombre de centres de cluster

${displaystyle k}$

est choisi à l’avance. Lorsque vous utilisez un inadapté

${displaystyle k}$

Des solutions complètement différentes, peut-être involontaires, peuvent survenir. Avec un “mauvais”

${displaystyle k}$

Je ne peux pas prendre de bons clusters. La solution est des valeurs différentes pour

${displaystyle k}$

Pour l’essayer, puis choisissez-en un, par exemple à l’aide du coefficient de silhouette, ou en comparant les différents coûts de regroupement.

Les groupes dans les données peuvent se chevaucher et fusionner de manière transparente les uns dans les autres, comme dans les épées montrées. Dans un tel cas peut k -Mesans ne séparent pas de manière fiable ces groupes car les données ne suivent pas le modèle de cluster utilisé.

De plus, la dépendance k -Mesans toujours convex (en raison de la minimisation de la distance à la mise au point du cluster). D’autres algorithmes tels que DBSCAN peuvent également trouver des grappes souhaitées “densément basées”. Quoi aussi de k -Les membres ne sont pas pris en charge sont des grappes hiérarchiques (c’est-à-dire des clusters, qui à leur tour ont une structure de cluster), tels que ceux-ci peuvent être trouvés avec l’optique, par exemple.

Enfin, chaque point est affecté à un cluster en K-means, il n’y a aucun moyen de reconnaître les valeurs aberrantes. Ceux-ci peuvent falsifier le résultat. Un remède peut être corrigé ici, ou d’autres algorithmes, tels que DBSCAN, qui reconnaissent automatiquement le bruit.

K-median [ Modifier | Modifier le texte source ]]

Dans l’algorithme K-Median, la distance de Manhattan est utilisée dans l’étape d’attribution au lieu de la distance euclidienne. Dans l’étape de mise à jour, la médiane est utilisée au lieu de la moyenne. ^{[douzième] [13]}

K-means ++ [ Modifier | Modifier le texte source ]]

L’algorithme K-Means ++ – ne choisit pas le cluster se concentre sur l’accident, mais selon le règlement suivant:

1. En tant que premier objectif principal du cluster, Chance un objet
2. Calculez la distance pour chaque objet
   ${displayStyle d (x)}$

   À la mise au point du cluster le plus proche

3. Sélectionnez un objet comme concentration du cluster suivant. La probabilité avec laquelle un objet sélectionné est proportionnel à
   ${displayStyle d ^ {2} (x)}$

   , d. H. Plus l’objet est supprimé de la mise au point déjà sélectionnée, plus il est probable qu’il soit sélectionné.

4. Répétez les étapes 2 et 3 à
   ${displaystyle k}$

   Les concentrations de cluster sont déterminées

5. Effectuez maintenant l’algorithme habituel de K-means

En règle générale, l’algorithme K-Means ultérieur converge en quelques étapes. Les résultats sont aussi bons qu’avec un algorithme K-Means habituel, mais l’algorithme est généralement presque deux fois plus rapide que l’algorithme K-Means. ^[14]

K-Médites (PAM) [ Modifier | Modifier le texte source ]]

L’algorithme PAM (partitionnement autour des Méoïdes, Kaufman et Rousseeuw, 1990) – connue également sous le nom de kéoïdes K ^[15] -Tour peut être interprété comme une variante de l’algorithme K-Mean, qui avec n’importe quel Distances convergées.

1. Choisir
   ${displaystyle k}$

   Objets comme cluster se concentre (Medoid)

2. Commandez chaque objet à la foyer du cluster suivant
3. Pour chaque concentration en cluster et chaque foyer sans cluster, les rôles sont excavés
4. Calculez la somme des distances ou moins que des similitudes pour chaque échange
5. Choisissez l’échange qui offre la plus petite somme à mesure que le nouveau cluster se concentre
6. Répéter 2.-5. Jusqu’à ce que le cluster se concentre ne change plus

Dans la version originale de PAM, la première étape – le choix des médoïdes initiaux – fait une grande partie de l’algorithme. Étant donné que seul le meilleur échange est effectué dans chaque itération, l’algorithme est presque déterministe (sauf pour exactement les mêmes distances). En conséquence, l’algorithme est généralement très lent.

Alors que K-Means minimise la somme des variances, les kédites K minimise les distances. En particulier, cet algorithme avec toutes les fonctions de distance peut être utilisé et garantit toujours.

Les images suivantes montrent une course d’un k -Means Algorithme pour déterminer trois groupes:

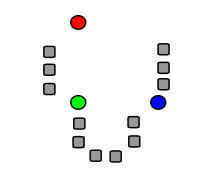	Trois centres de cluster ont été choisis.
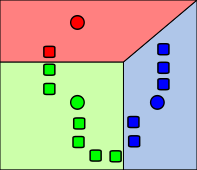	Les objets (points de données) représentés par des rectangles sont affectés au cluster avec le centre de cluster suivant.
	Les centres (concentration respective) des grappes sont recalculés.
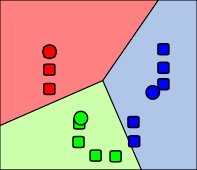	Les objets sont à nouveau redistribués et affectés au cluster, dont le centre est le plus proche.

Dans le traitement d’image, le k -Leans algorithme souvent utilisé pour la segmentation. En tant que mesure de distance, la distance euclidale n’est souvent pas suffisante et d’autres fonctions de distance, basées sur des intensités de pixels et des coordonnées de pixels, peuvent être utilisées. Les résultats sont utilisés pour séparer le premier plan et le fond et pour la reconnaissance des objets. L’algorithme est répandu et est dans des bibliothèques de traitement d’image communes telles que OpenCV, Scikit Image ^[16] et ITK implémenté.

K-Means et ses variantes sont disponibles dans divers logiciels open source.

• Dlib ^[17]
• Elki contient les variantes de Lloyd et MacQueen, ainsi que diverses stratégies pour les valeurs de départ telles que K-Means ++ et les variantes d’algorithme telles que les K-Mediens, les K-Médoïdes et le PAM.
• GNU R contient les variantes de Hartigan, Lloyd et MacQueen, et des variations supplémentaires dans le package d’extension “FlexClust”.
• OpenCV contient une version de K-means (y compris K-means ++ semis) optimisée pour le traitement d’image)
• Scikit-Learn contient des k-means, y compris la variante d’Elkan et K-means ++.
• Weka contient des k-means (y compris l’ensemencement K-means ++) et l’expansion des mi-moyens.

• David Mackay: Algorithmes de théorie de l’information, d’inférence et d’apprentissage . Cambridge University Press, 2003, ISBN 0-521-64298-1, chapitre 20. Un exemple de tâche d’inférence: clustering, S. 284–292 ( inference.phy.cam.ac.uk [PDF]).
• Gary Bradski, Adrian Kaehler: Apprentissage de la vision de l’ordinateur OpenCV avec la bibliothèque OpenCV . O’Reilly, 2001, ISBN 978-0-596-51613-0.