Chaîne de chaîne (mathématiques) – Wikipedia

Un Chaîne de chaîne (aussi Seilur , Chainid ou Courbe de chaîne , Anglais caténaire ou courbe funiculaire ) est une courbe mathématique qui décrit la pente d’une chaîne suspendue à ses extrémités sous l’influence de la gravité. C’est une fonction mathématique élémentaire, le cosinus hyperbolique, court matraque .

Première dérivation: minimum d’énergie potentielle [ Modifier | Modifier le texte source ]]

Le calcul de la ligne de chaîne est un problème classique du calcul de la variation. Vous pensez à une corde d’une certaine étendue et longueur qui est accrochée à ses extrémités. La courbe de corde est le résultat de la plus petite énergie potentielle possible de la corde. Vous essayez de comprendre cela mathématiquement.

Pour ce faire, vous avez besoin de l’expression mathématique pour l’énergie potentielle. C’est un raffinement de la “taille de poids” bien connue ”

${displaystyle mgh}$

. Le raffinement est que l’énergie est évaluée séparément pour “toutes les parties” de la corde et additionnée. Ceci est nécessaire car les parties de la corde sont à différentes hauteurs. La dégradation mentale de la corde en parties toujours plus petites fait partie intégrante de la somme. La hauteur

${displaystyle h}$

hors de

${displaystyle mgh}$

Est par la fonction que vous recherchez

${displayStyle y (x)}$

remplacé, la masse

${displaystyle m}$

à travers la masse

${displayStyle Mathrm {d} m}$

de la corde sur l’intervalle

${displayStyle [x, x + mathrm {d} x]}$

; Selon Pythagore, c’est:

${DisplayStyle Mathrm {d} m = mu {sqrm {d} x) + (mathrm {d} y) y) ^}}} x = mu {sqrt {1 + y ‘^ {2}}, mathrm {d} x}$

par lequel

${displaystyle mu}$

La masse par mètre est. Quand la corde dans les lieux

${displayStyle x_ {1}}$

,

${displayStyle x_ {2}}$

est suspendu, les résultats de l’énergie (“poids parfois de la hauteur”)

${displayStyle e = mu g, int _ {x_ {1}} ^ {x_ {2}} mathrm {d} x; y, {sqrt {1 + y ‘^ {2}}}}$

Une considération similaire conduit à l’expression de la longueur de la corde:

${displayStyle l = int _ {x_ {1}} ^ {x_ {2}} mathrm {d} x {sqrt {1 + y ‘^ {2}}}}$

L’énergie doit être minimisée, mais la longueur est spécifiée. Ceci est amené sous un seul chapeau par un multiplicateur Lagrange

${displayStyle mu gy_ {0}}$

, c’est-à-dire que vous minimisez maintenant l’expression

${DisplayStyle e, -, mu gy_ {0}, l = mu g, int {x_ {1}}} mathrm {1 + y ‘^ {2}}}, (y, -y_ ​​{0})}$

La variation entraîne l’équation différentielle (équation d’Euler-Lagrange):

${DisplayStyle (y-and_ {0}) et ”, – et ‘^ {2}, =, 1}$

Fait intéressant, dans cette étape, les deux taille de masse sont

${displaystyle mu}$

ainsi que l’accélération sévère

${displaystyle g}$

tombé. Une corde lourde prend ainsi la même forme que facile, et malgré une autre accélération de cas, la même forme entraîne la lune que sur Terre.

Les solutions de l’équation sont les fonctions

${displayStyle y (x), =, acdot cosh gauche ({frac {x-x_ {0}} {a}} droit) + y_ {0}}$

Ce sont des fonctions hyperboliques en cosinus élargies et décalées.

${displaystyle a}$

est le rayon de courbure dans l’apex (voir illustration) et en même temps le facteur d’agrandissement.

${displayStyle x_ {0}}$

Est le changement dans

${displaystyle x}$

-Direction,

${displaystyle y_ {0}}$

Le passage dans

${displaystyle y}$

-Direction.

La forme en béton que la corde accepte finalement est calculée par

${displayStyle x_ {0}}$

,

${displaystyle y_ {0}}$

et

${displaystyle a}$

De cette façon, adapte que la courbe passe par les points suspendus et la longueur spécifiée

${displaystyle l}$

a.

Deuxième dérivation: programme parallèle [ Modifier | Modifier le texte source ]]

Avec un poids du poids, qui est plus de deux cordes de maintien _d’abord et s ₂ Avec les gradients t _d’abord et T ₂ est accroché à un total de deux colonnes, les forces sur les cordes sont faites par un parallélogramme avec la force de maintien F _H décrit comme diagonal. Le vecteur de la force de maintien f _H forme le vecteur de poids f _g le même compteur-vecteur. Le parallélogramme est divisé en deux triangles congruents par le vecteur de puissance de maintien. Avec l’ensemble sinus, les quantités des deux forces de traction sur les cordes f peuvent _S1 et f _S2 être calculé:

${displayStyle | {vec {f}} _ {s1} | = | {vec {f}} _ {g} | sin [{tfrac {1} {2}} pi -arctan (t_ {2})] csc [arctan (t_ {2}) – arcTan (t_ {1})$

${displayStyle | {vec {f}} _ {s2} | = | {vec {f}} _ {g} | sin [{tfrac {1} {2}} pi + arctan (t_ {1})] csc [arctan (t_ {2}) – arcTan (t_ {1})$

Avec deux morceaux de poids des mêmes poids lourds, chacun accroché à leur colonne associée à une corde de maintien et avec une autre corde de maintien s _M La loi suivante s’applique au poids du poids dans la corde commune moyenne:

${displayStyle | {vec {f}} _ {g} | sin [{tfrac {1} {2}} pi + arctan (t_ {l})] csc [arctan (t_ {m}) – arctan (t_ {l})] = | {vec {f}} {g} {2}} pi -arctan (t_ {r})] csc [arctan (t_ {r}) – arctan (t_ {m})]}$

${Displaytlele sin [{{spe_ {wrimed {1}} + arctan (t _ {l}) sin [{{l}) – arctan (t _ {r}) – arctan (t _ {r})]$

${displayStyle {frac {t_ {r} -t_ {m}} {sqrt {(t_ {l} ^ {2} +1) (t_ {m} ^ {2} +1) (t_ {r} ^ {2} +1)}}} = {frac {T_ {m} – {l}}}}} {frac {T_ {m} – {l}}}}} {FRAC {T_ {M} – {l}}}}} {FRAC {T_ {M} -T_ t {(t_ {l} ^ {2} +1) (t_ {m} ^ {2} +1) (t_ {r} ^ {2} +1)}}}}$

${displayStyle t_ {r} -t_ {m} = t_ {m} -t_ {l}}$

Il y a t _L La pente de la corde S _L , t _M Est la pente de la corde S _M et T _R Est la pente de la corde S _R .

Avec une chaîne d’un total de M cordes et M – 1 des poids tout aussi lourds entre les cordes, la différence par rapport à la pente d’une corde moins la pente de la corde prédécesseur a toujours la même valeur:

${displayStyle t_ {2} -t_ {1} = t_ {3} -t_ {2} = t_ {n + 1} -t_ {n} opératorname {, mit, allen}, nin mathbb {n} leq m-1}$

En raison de l’égalisation de toutes les longueurs de corde et du rapprochement des longueurs rapides pour zéro, la chaîne se développe comme une valeur frontalière M contre la chaîne infinie en une courbe de chaîne idéale. Ainsi, avec une courbe de chaîne idéale, la pente de la courbe est linéaire à la longueur de la courbe. La pente est donc directement proportionnelle à la dimension de l’arc au minimum relatif de la courbe. La fonction qui a cette proportionnalité directe entre les virages et la longueur des virages dans votre graphique est le cosinus Hyperbolicus. Dans l’équation différentielle suivante, la longueur de la courbe est donnée comme une partie intégrante du successeur pythagorien de la dérivation et de la pente comme une dérivation elle-même:

${displayStyle int _ {x_ {0}} ^ {x} {sqrt {{bigl [} {frac {mathrm {d}} {mathrm {d} x}} y (x) (x = w) {bigr]} ^ {2} +1}}, mathrm {d} w = a,} {d}} {mathrm {d} x}} y (x)}$

${displayStyle y (x) = acosh [(x-x_ {0}) / a] + y_ {0}}$

Long [ Modifier | Modifier le texte source ]]

La courbe de chaîne est-elle une équation

${displayStyle y = acosh gauche ({frac {x} {a}} droit)}$

donné et traverse les points suspendus

${displayStyle (x_ {1}, y_ {1})}$

et

${displayStyle (x_ {2}, y_ {2})}$

, s’applique alors à la différence de hauteur

${DisplayStyle V}$

les points:

${affichestyle v: = y_ {2} -y_ {1} = acosh gauche ({frac {x_ {2}} {a}} droit) -ACOSH Left ({frac {x_ {1}} {a}} droit)}$

Et pour la longueur

${displaystyle l}$

Ce qui suit s’applique entre les points suspendus de la courbe de chaîne:

${displaystyle l=int _{x_{1}}^{x_{2}}{sqrt {1+y’^{2}}}mathrm {d} x=int _{x_{1}}^{x_{2}}{sqrt {1+left({frac {mathrm {d} }{mathrm {d} x}}acosh left({frac {x}{a}}right)right)^{2}}}mathrm {d} x=int _{x_{1}}^{x_{2}}{sqrt {1+sinh ^{2}left({frac {x}{a}}right)}}mathrm {d} x=int _{x_{1}}^{x_{2}}cosh left({frac {x}{a}}right)mathrm {d} x=asinh left({frac {x_{2}}{a}}right)-asinh left({frac {x_{1}}{a}}right)}$

Pour la dérivation, la fonction de dérivation et la fonction régulière du sinus hyperbolique et de Kosinus hyperbolicus et de l’équation étaient

${displayStyle Cosh ^ {2} x !; – sinh ^ {2} x = 1}$

utilisé. Des deux équations dérivées et des théorèmes d’addition

${DisplayStyle Cosh Left (X-YRIGM$

et

${DisplayStyle Cosh Left (2xRight) = 2Sinh ^ {2} Left (xRight) +1}$

Suit:

${affichestyle l ^ {2} -v ^ {2} = gauche (asinh Left ({frac {x_ {2}} {a}} droit) -asinh Left ({frac {x_ {1}} {a}} droit) à droite) ^ {2} -left (ACOSH gauche -ACOSH gauche ({frac {x_ {1}} {a}} à droite) à droite) ^ {2} = 2a ^ {2} Left (Cosh Left ({frac {x_ {2} -x_ {1}} {a}} droit) -1Right) = 4a ^ {2} Sin _ {1}} {2a}} à droite)}$

Exemple 1 [ Modifier | Modifier le texte source ]]

Un exemple est un entre deux messages (distance

${displayStyle in}$

) Corde hangée de la longueur

${displaystyle l}$

donné (voir figure). Les messages sont les mêmes et sont à

${displayStyle x = – {tfrac {w} {2}}}$

et

${displayStyle x = + {tfrac {w} {2}}}$

Donc ça s’applique

${displayStyle x_ {0} = 0}$

.

Au rayon de courbure

${displaystyle a}$

Pour calculer, nous écrivons la longueur de la corde

${displaystyle l}$

En tant que fonction de

${displaystyle a}$

:

${displayStyle l = int _ {- w / 2} ^ {w / 2} {sqrt {1 + y ‘^ {2}}}, mathrm {d} x = 2a, sinh gauche ({frac {w} {2a}} droit)}$

.

Cette relation pose

${displaystyle a}$

en dépendance de

${displayStyle in}$

et

${displaystyle l}$

clairement ferme. Puisque vous n’avez pas d’expression fermée pour

${displaystyle a}$

Peut spécifier, la valeur avec une procédure numérique pour la solution des équations non linéaires doit être calculée plus approximativement.

Cependant, sont

${displaystyle h}$

et

${displaystyle l}$

donné, peut

${displaystyle a}$

et

${displayStyle in}$

comme suit fermé être représenté.
Le carré provient de l’équation (ci-dessus)

${displayStyle textStyle {frac {1} {2}} l = acdot sinh gauche ({frac {{frac {1} {2}} w} {a}} droit)}$

Du carré de l’équation (ci-dessus)

$gens$

soustrait, puis l’équation créée avec les résultats de la différence

${displaystyle textstyle a ^ {2} cdot overbrace {Left (Cosh ^ {2} Left ({frac {{frac {1} {2}} w} {a}} à droite) -Sinh ^ {2} Left ({Frac {{frac {1} {2}}} {a-{) 1} = (h + a) ^ {2} -left ({frac {1} {2}} lright) ^ {2}}$

,,
à partir duquel

${displayStyle in}$

à cause de

${DisplayStyle Cosh ^ {2} (xi) -Sinh ^ {2} (xi) = 1}$

éliminé et après

${displayStyle textStyle a = {frac {1} {2}} hcdot gauche (gauche ({frac {{frac {1} {2}} l} {h}} droit) ^ {2} -1Right)}$

peut être changé.
Insérer ceci

${displaystyle a}$

dans

${displayStyle w = 2acdot opératorname {arsinh} Left ({frac {{frac {1} {2}} l} {a}} droit)}$

Et les transformations entraînent l’expression exposée pour la distance sous forme fermée z. B.

${displayStyle textStyle w = 2hcdot gauche (gauche ({frac {l} {2h}} droit) ^ {2} -1Right) CDOT Operatorname {ArtanH} Left ({frac {2h} {l}} droite)}$

ou

${displayStyle textStyle l = 2Hcdot Left (Left ({frac {w} {2h}} droite) ^ {2} + 1Right) cdot operatorname {tanh} Left ({frac {2h} {w}} droite)}$

.

Enfin vous lisez l’état de l’illustration

${displayStyle y ({tfrac {w} {2}}) = 0}$

à partir de laquelle

${displaystyle y_ {0}}$

reçoit. Les relations s’appliquent également

${displayStyle {begin {aligned} {frac {b} {a}} & = cosh Left ({frac {w} {2a}} droit) \ b & = h + a, end {alignement}}}$

par lequel

${displaystyle h}$

La “pente” est.

L’énergie potentielle de ce système est

${displayStyle e = – {frac {mu g} {2}} (l, b-w, a)}$

.

Plus précisément, c’est la différence d’énergie par rapport au cas que la corde est complètement au niveau des points de suspension (

${displayStyle y = 0}$

).

Avec l’aide de l’énergie, vous pouvez

${displaystyle f}$

Calculez dans les points suspendus. Pour ce faire, imaginez que la corde fonctionne dans un point suspendu sur un jet de déviation qui redirige la force dans la direction horizontale. Autour de la corde comme indiqué par un très petit itinéraire

${DisplayStyle DS}$

Pour vous retirer, vous devez

${displaystyle dE=Fds}$

dépenser. Cela peut être calculé et reçoit ainsi la force

${displayStyle f = {tfrac {de} {ds}}}$

. Calculer

${displaystyle dE}$

Si vous comparez l’énergie de la corde d’origine avec celle de la UM

${DisplayStyle DS}$

corde raccourcie. Le résultat est étonnamment simple, à savoir

${displayStyle f = mu gb = mu g (h + a) = {frac {mg} {2}} coth gauche ({frac {w} {2a}} droit)}$

avec

${DisplayStyle m = mu, l}$

. La même formule peut également être appliquée à certaines parties de la corde. Puisque les sections sont toutes le même rayon de courbure

${displaystyle a}$

avoir, mais pour les petites sections (ci-dessous dans la vallée) la pente

${displaystyle h}$

devient négligeable, il y a la tension de la corde dans la vallée de la corde

${Affichestyle lui gi}$

.

Si vous mettez les poteaux proches, la pente domine

${displaystyle h}$

, qui est alors une moitié de la longueur de la corde. Comme prévu, la force est la moitié du poids de la corde,

${displayStyle {tfrac {mg} {2}}}$

(Notez que deux points suspendus partagent la charge).

La formule montre également comment la résistance avec l’augmentation de la tension de la corde est un demi-poids par le facteur

${displayStyle coth ({tfrac {w} {2a}})}$

dépasse. Le facteur est pratiquement 1 pour de très petits rayons de courbure

${displaystyle a}$

, mais grossièrement

${displayStyle {tfrac {2a} {w}}}$

ou

${displayStyle {tfrac {2a} {l}}}$

Pour de très grands rayons de courbure.

Dans la vie quotidienne, le facteur est d’environ 2 à 4. Au point de suspension, le poids entier ou le double de la corde est.

Exemple 2 [ Modifier | Modifier le texte source ]]

Pour

${displaystyle a}$

= 100 m et un écart de mât

${displayStyle in}$

de 200 m (cas spécial

${displayStyle w / 2 = a}$

) Une corde de 2 · 117,5 m de long est requise:

${DisplayStyle l / 2 = acdot naissance (1)}$

. La pente est de 54 m. Pour un câble en acier avec une section transversale de 100 cm², une moitié de corde pèse 9,2 t. Le poids correspondant de 9 · 10 ⁴ N est la force verticale sur une suspension. La force horizontale sur une suspension est de 7,7 · 10 ⁴ N.

S’élève à

${displaystyle a}$

Environ 20,2% de la largeur totale

${displayStyle in}$

, c’est la pente

${displayStyle y (x = w / 2)}$

Comme la largeur

${displayStyle in}$

(Dimensions totales carrées). Ce cas est disponible, par exemple, par l’arc de passerelle (voir ci-dessous dans la section architecture ), qui mesure 630 pieds de large et tout aussi haut. La formule exacte

$gens$

avec un = 127,7 pieds et Dans / 2 = 315 pieds est exposé à l’intérieur du monument. Néanmoins, le bâtiment ne forme pas de ligne de chaîne, à proprement parler, en raison de la variation de la force de l’arc.

Exemple 3 [ Modifier | Modifier le texte source ]]

Deux colonnes des hauteurs g = 1 m et h = 2 m sont à une distance de D = 3 m de l’autre.

Une chaîne de longueur k = 4 m est suspendue entre eux.

Question 1: Quelle est la taille du rayon de courbure de cette courbe de chaîne? Synthèse des formules: En supposant qu’en entrant dans un système de coordonnées, la pointe du pilier G comme début de la chaîne sur le point (0, g) et le haut de la colonne H à l’extrémité de la chaîne est sur le point (d, h), le système d’équations suivant s’applique: JE) ${displaystyle h-g=acosh[(d-x_{text{SP}})/a]-acosh(-x_{text{SP}}/a)}$ Ii) ${displaystyle k=asinh[(d-x_{text{SP}})/a]-asinh(-x_{text{SP}}/a)}$ La différence de hauteur de la chaîne est décrite par le cosinus hyperbolique. La longueur de la chaîne est décrite par le sinus hyperbolique. Les théorèmes des fonctions d’hyperbole permettent les conversions de sommes en produits: JE) ${displaystyle h-g=2asinh {bigl (}{frac {d}{2a}}{bigr )}sinh {bigl (}{frac {d-2x_{text{SP}}}{2a}}{bigr )}}$ Ii) ${displaystyle k=2asinh {bigl (}{frac {d}{2a}}{bigr )}cosh {bigl (}{frac {d-2x_{text{SP}}}{2a}}{bigr )}}$ Avec le théorème d’addition de l’Hyperbolicus cosinus, ce qui suit de la combinaison II² – I² est créé par le paramètre ${displayStyle x_ {text {sp}}}$ Formule libérée: Iii) ${displaystyle 4a^{2}sinh {bigl (}{frac {d}{2a}}{bigr )}^{2}=k^{2}-(h-g)^{2}}$ Avec cette formule, la valeur de A peut être calculée directement. Utilisation des valeurs: En insérant les valeurs mentionnées pour G, H, D et K, cette valeur pour A: Valeurs: g = 1 m, h = 2 m, d = 3 m, k = 4 m Détermination du rayon de courbure: Iii) ${displaystyle 4a^{2}sinh {bigl (}{frac {3m}{2a}}{bigr )}^{2}=15m^{2}}$ ${displaystyle a={color {BlueGreen}1,182m}}$ Répondre: Le rayon de courbure de cette courbe de chaîne est de 1,182 m.

Question 2: À quelle distance se trouve l’apex de la colonne G? Synthèse des formules: Ces formules proviennent du traitement de la première question partielle: JE) ${displaystyle h-g=2asinh {bigl (}{frac {d}{2a}}{bigr )}sinh {bigl (}{frac {d-2x_{text{SP}}}{2a}}{bigr )}}$ Ii) ${displaystyle k=2asinh {bigl (}{frac {d}{2a}}{bigr )}cosh {bigl (}{frac {d-2x_{text{SP}}}{2a}}{bigr )}}$ Par la facture I / II et la résolution ultérieure selon ${displayStyle x_ {text {sp}}}$ Cette formule est créée: Iv) ${displaystyle x_{text{SP}}={frac {1}{2}}d-aoperatorname {artanh} {bigl (}{frac {h-g}{k}}{bigr )}}$ Utilisation des valeurs: Détermination de la distance du sommet pointer vers le pilier G: Iv) ${displaystyle x_{text{SP}}={frac {3m}{2}}-{color {BlueGreen}1,182m}operatorname {artanh} {bigl (}{frac {1m}{4m}}{bigr )}}$ ${displaystyle x_{text{SP}}={color {ForestGreen}1,198m}}$ Répondre: L’apex est à 1,198 m de la colonne G.

Question 3: Quelle est la hauteur de l’apex? Synthèse des formules: L’équation de la chaîne générale s’applique: ${displaystyle y(x)=acosh {bigl [}(x-x_{SP})/a{bigr ]}+y_{text{VE}}}$ Si la valeur ${displayStyle x = 0}$ est utilisé, alors cette équation émerge: ${displaystyle g=acosh(-x_{text{SP}}/a)+y_{text{VE}}}$ Cette équation est dissoute en fonction du report ordonné: ${displaystyle y_{text{VE}}=g-acosh(x_{text{SP}}/a)}$ Et cette formule s’applique directement à l’apex recherché en insérant la valeur ${DisplayStyle x = x_ {texte {sp}}}$ : ${displaystyle y(x_{text{SP}})=a+y_{text{VE}}}$ La formule suivante mène directement à la hauteur de l’apex: DANS) ${displaystyle y(x_{text{SP}})=a+g-acosh(x_{SP}/a)}$ Utilisation des valeurs: Les valeurs g, a et ${displayStyle x_ {text {sp}}}$ sont insérés dans l’équation V: DANS) ${displaystyle y(x_{text{SP}})={color {BlueGreen}1,182m}+1m-{color {BlueGreen}1,182m}cosh({color {ForestGreen}1,198m}/{color {BlueGreen}1,182m})}$ ${displaystyle y(x_{text{SP}})={color {LimeGreen}0,339m}}$ Répondre: L’apex mesure 0,339 m de haut.

parabole [ Modifier | Modifier le texte source ]]

Joachim Junge a déclaré en 1639 que la ligne de chaîne n’était pas une parabole. Gottfried Leibniz, Christiaan Huygens et Johann I Bernoulli ont découvert en 1690/91 comment former la courbe de la chaîne. ^[d’abord] Si vous regardez le développement de la ligne de la ligne de chaîne, vous pouvez voir qu’il s’agit d’une somme infinie de termes de toutes les fonctions rationnelles des degrés de comptage des tiges:

${displayStyle {a} cosh ({frac {x} {a}}) = asum _ {n = 0} ^ {infty} {frac {x ^ {2n}} {(2n)! ^ {4}} {24a ^ {3}}} + {frac {x ^ {6}} {720a ^ {5}}} + DOTS}$

Pour suffisamment de petites quantités de

${displaystyle x}$

Vous pouvez annuler le deuxième lien à tour de rôle, puis obtenir une parabole carrée comme courbe d’approximation dans la zone de l’apex, qui, cependant, (sauf à l’apex lui-même) est toujours “en dessous” de la ligne de chaîne réelle, i. H. fournit des valeurs trop petites.

Une parabole carrée, d’autre part

${displaystyle x}$

Charge de route distribuée, par ex. B. Un pont de suspension, à condition que le poids des cordes puisse être négligé par rapport à la route. (Si cette dernière condition n’est pas remplie et que les cordes de transport constituent donc une partie significative du poids global, le calcul de la courbe de corde sous la forme d’une fonction fermée n’est pas possible).

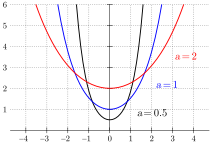
L’illustration à droite compare le cours de courbe d’une ligne de chaîne (rouge) avec celle d’une parabole normale (verte).

Katénoïde [ Modifier | Modifier le texte source ]]

Celui en faisant tourner la ligne de chaîne autour du X -E aire de rotation générée par axe een Katénoïde En plus du niveau, et est la seule zone rotative qui est également une zone minimale: les katénoïdes sont statiques pour être considérés comme des formes de toit idéales pour les tours rondes, car ils se portent (théoriquement).
Si vous tenez deux anneaux côte à côte et plongez dans une solution de savon pour les couvrir d’une peau de savon, un katénoïde se forme entre les anneaux.

Tractrix [ Modifier | Modifier le texte source ]]

La ligne de chaîne est l’évolue vers le tractrix (courbe de glisser).

L’une des lignes de support analogiques de la ligne de chaîne suit la feuille sans cisaillement:

• Le Bac nubien , un coffre-fort est une variante du Voûte nubienne , une manière voûtée dans la construction d’argile sans coffrage et souvent sans enseignements qui ont son nom de conceptions traditionnelles en Nubie. Afin d’atteindre la plus grande stabilité possible, la ligne de support suit généralement la ligne de chaîne.
• Un premier exemple européen est le dôme de la cathédrale St Paul à Londres, qui a été construit par Christopher Wren après 1666, qui mesurait 30,80 m de diamètre. ^[2] Entre un hémisphère en bois extérieur et intérieur, il avait placé un katénoïde qui a pris la gravité de la lanterne, mais a même permis de construire moins. La courbe était encore empiriquement approximée à l’époque.
• Auguste de Montferrand a transformé le dôme dans la cathédrale Saint-Paul dans la construction du dôme de fer de l’isaakskathedral à Saint-Pétersbourg (1838-1841) et a utilisé un nouveau milieu en construction avec du fer. Le dôme de fer de Montferrand lui-même est devenu un modèle pour le dôme de fer de la Capitole à Washington (1855–1866). ^[3]
• La section croisée du toit de la station Budapest OST (Keleti) (Hongrie) forme une ligne de chaîne. Construit à partir de 1881/84. Constructeur: János Feketeházy.
• Antoni Gaudí a utilisé le principe de construction qui était basé sur cela, y compris à la Sagrada Família à Barcelone. Le modèle de l’église similaire de la Colònia Güell a également été déterminé empiriquement, à savoir la «tête de côté» en suspendant des cordes avec des poids correspondants (vers 1900; Original perdu dans un incendie))

1. ↑ Edward Harrington Lockwood: Un livre de courbes . Cambridge University Press, 1971, S. 124 .
2. ↑ Karl-Eugen Kurrer: HISTOIRE DE LA STATIQUES DE CONSTRUCTION , S. 141
3. ↑ Fedorov (PDF; 6,2 MB), dans: bautechnikgeschichte.files.wordpress.com