UN Multiprendre Est un pendule qui pendait d’autres pendules sur le bras. Un modèle de mouvement imprévisible est créé, qui varie considérablement même avec les troubles mineurs. Les processus chaotiques sont faciles à simuler, c’est pourquoi il est devenu un modèle populaire dans la théorie du chaos.
Le modèle du multiple
 Le niveau -te est un système idéalisé d’un pendule en filetage, à son point de masse oscillant
Le niveau -te est un système idéalisé d’un pendule en filetage, à son point de masse oscillant
 Un pendule de threads identiques supplémentaires est lié. Les fils de connexion entre le point suspendu et les points de masse sont considérés comme des tiges complètement non épu et sans masse. L’ensemble du système est compris comme sans frottement.
Un pendule de threads identiques supplémentaires est lié. Les fils de connexion entre le point suspendu et les points de masse sont considérés comme des tiges complètement non épu et sans masse. L’ensemble du système est compris comme sans frottement.
Les équations de mouvement pour un multiple
 -Te niveau peut être dérivé avec le deuxième type de formalisme de lagrange.
-Te niveau peut être dérivé avec le deuxième type de formalisme de lagrange.
Coordonnées généralisées [ Modifier | Modifier le texte source ]]
En utilisant la trigonométrie que vous obtenez:




…


En conséquence, les coordonnées cartésiennes peuvent
 des points de masse
des points de masse
 pour
pour
 ∈ {1, …,
∈ {1, …,
 } et leurs dérivations temporelles sont écrites sous la forme suivante:
} et leurs dérivations temporelles sont écrites sous la forme suivante:




Fonction Lagrange [ Modifier | Modifier le texte source ]]
Énergie cinétique
 et potentiel
et potentiel
 résultat:
résultat:


Ainsi, la fonction Lagrange est
 :
:
![L(varphi_1,...,varphi_n,dot{varphi}_1,...,dot{varphi}_n) = frac{1}{2} sum_{k=1}^{n} m_k left[left(sum_{i=1}^{k} l_i dot{varphi}_i cosvarphi_iright)^2+left(sum_{i=1}^{k} l_i dot{varphi}_i sinvarphi_iright)^2right] + g sum_{k=1}^{n} sum_{i=1}^{k} m_k l_i cosvarphi_i](https://wikimedia.org/api/rest_v1/media/math/render/svg/5864004a43716bfd3db60cd612f8ca0ae6096e4d)
Équations de mouvement [ Modifier | Modifier le texte source ]]
Les équations de la multiprendula n -Le résultat niveau de

ou.

pour
 ∈ {1, …,
∈ {1, …,
 }.
}.
Les équations de mouvement pour les coordonnées généralisées (
 ) fournir un système non linéaire de
) fournir un système non linéaire de
 Équations différentielles du deuxième ordre, qui pour
Équations différentielles du deuxième ordre, qui pour

 agence connue, par exemple les valeurs de départ
agence connue, par exemple les valeurs de départ

Peut être résolu à l’aide de procédures numériques. De petits angles peuvent être fabriqués pour simplifier les équations de mouvement.
Pour les étapes
 Pendule mathématique [ Modifier | Modifier le texte source ]]
Pendule mathématique [ Modifier | Modifier le texte source ]]
Pour
 Le cas simple des résultats du pendule mathématique.
Le cas simple des résultats du pendule mathématique.
Voici l’énergie cinétique
 et potentiel
et potentiel
 pour
pour


avec
 .
.
En conséquence, l’équation du mouvement est:

Avec l’approche de petit angle
 L’équation peut être simplifiée:
L’équation peut être simplifiée:

Une solution fonctionnelle à l’équation de mouvement est
 ,
,
de sorte que dans les conditions de départ connues pour le paramètre
 est applicable:
est applicable:

Le pendule balance harmonieusement avec la période:

Doppelpendel [ Modifier | Modifier le texte source ]]
L’affaire
 représente le double pendule.
représente le double pendule.
Voici l’énergie cinétique
 et potentiel
et potentiel
 pour:
pour:


En conséquence, les équations de mouvement sont:

et

Un exemple de double pendule est une cloche avec une dentelle.
Tripelpendel [ Modifier | Modifier le texte source ]]
L’affaire
 met ça Tripelpendel mais.
met ça Tripelpendel mais.
Il en résulte l’énergie cinétique
 pour:
pour:


Pour le potentiel
 est applicable:
est applicable:

En conséquence, les équations de mouvement sont:


et


et

Simulation des trajectoires [ Modifier | Modifier le texte source ]]
- Georg Hamel: Mécanique théorique . Springer, Berlin 1967. Réimpression appropriée 1978, ISBN 3-540-03816-7
- Friedhelm Kuypers: Mécanique classique . 5e édition. VCH, Weinheim 1997, ISBN 3-527-29269-1
- LANDAU / LIFSCHITZ: Manuel de physique théorique. Volume 1: Mécanique . 14e édition. Allemand, Thun 1997, ISBN 3-8171-1326-9
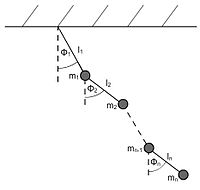
 Le niveau -te est un système idéalisé d’un pendule en filetage, à son point de masse oscillant
Le niveau -te est un système idéalisé d’un pendule en filetage, à son point de masse oscillant  Un pendule de threads identiques supplémentaires est lié. Les fils de connexion entre le point suspendu et les points de masse sont considérés comme des tiges complètement non épu et sans masse. L’ensemble du système est compris comme sans frottement.
Un pendule de threads identiques supplémentaires est lié. Les fils de connexion entre le point suspendu et les points de masse sont considérés comme des tiges complètement non épu et sans masse. L’ensemble du système est compris comme sans frottement. 





 des points de masse
des points de masse  pour
pour  ∈ {1, …,
∈ {1, …, 



 et potentiel
et potentiel  résultat:
résultat: 

 :
: ![L(varphi_1,...,varphi_n,dot{varphi}_1,...,dot{varphi}_n) = frac{1}{2} sum_{k=1}^{n} m_k left[left(sum_{i=1}^{k} l_i dot{varphi}_i cosvarphi_iright)^2+left(sum_{i=1}^{k} l_i dot{varphi}_i sinvarphi_iright)^2right] + g sum_{k=1}^{n} sum_{i=1}^{k} m_k l_i cosvarphi_i](https://wikimedia.org/api/rest_v1/media/math/render/svg/5864004a43716bfd3db60cd612f8ca0ae6096e4d)


 ∈ {1, …,
∈ {1, …,  ) fournir un système non linéaire de
) fournir un système non linéaire de 
 agence connue, par exemple les valeurs de départ
agence connue, par exemple les valeurs de départ 
 Le cas simple des résultats du pendule mathématique.
Le cas simple des résultats du pendule mathématique. 

 .
. 
 L’équation peut être simplifiée:
L’équation peut être simplifiée: 
 ,
,  est applicable:
est applicable: 

 représente le double pendule.
représente le double pendule. 



 met ça Tripelpendel mais.
met ça Tripelpendel mais. 







Recent Comments