Viereck – Wikipedia

Quelques types de carré

UN carré (aussi Quadrilatère , Quadrangel ou Quadrilatère ) est une figure de la géométrie de niveau, à savoir un mousseur multiples avec quatre coins et quatre côtés. Le triangle analogue est également une généralisation du terme carré sur les géométries non taxes ( incurvé Carré) possible. Dans la géométrie projective, le carré complet et le double côté complet jouent un rôle important. Dans la géométrie finie, les propriétés d’incidence du carré sont utilisées pour définir le terme «carré généralisé».

Différence entre le circuit tendon et le plus petit cercle environnant

Un carré a deux diagonales. Si les deux diagonales sont dans le carré, le carré est convexe, si exactement une diagonale est à l’extérieur, c’est le nom du carré. Le carré est le polygone le plus simple qui puisse être concave. À recouvrir Viereck sont tous deux des diagonales à l’extérieur du carré, par exemple avec le trapèze enchevêtré. Les carrés débordés sont des polygones généralisés et ne sont généralement pas comptés sur le carré. de même pour dégénérer Les plafonds touristiques dans lesquels deux ou plusieurs points d’angle s’effondrent ou plus de deux points clés sont en ligne droite.

La somme de l’angle intérieur dans le carré est à 360 ° car chaque carré peut être décomposé en deux triangles.

Un trapèze est un carré avec au moins deux côtés parallèles. S’il y a deux pages en face de l’autre en parallèle, on parle du parallélogramme. Un carré, qui a quatre angles intérieurs de 90 °, c’est-à-dire les angles droits, est un rectangle. Un rectangle qui a quatre pages de la même longueur est un carré. Le carré est le carré régulier.

Pendant le cerf-volant du dragon (deltoïde), la diagonale est verticale et une diagonale est divisée par deux par l’autre. Ceci est synonyme du fait qu’il y a deux paires de pages voisines, chacune étant de la même longueur. Sur quatre côtés de la même longueur, on parle d’un diamant (rhombus). Un carré est un diamant avec quatre angles intérieurs de la même taille.

Dans le cas d’un tendon à long terme, les quatre côtés sont des tendons de la zone. Si les quatre côtés sont tangents d’une rencontre, on parle d’un quart de la tangente.

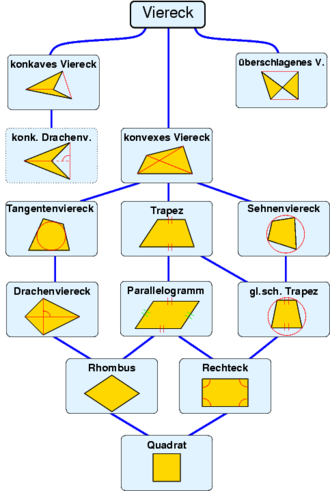
Entre les types carrés individuels s’appliquent, en particulier les sous-quantités montrées dans l’illustration, telles que

• Rectangles carrés ⊂ parallélogramme ⊂ trapèze ⊂ carré convexe ⊂ carré

Les carrés sont un sous-ensemble des rectangles, les rectangles sont une quantité partielle des parallélogrammes, etc.

Les relations suivantes s’appliquent également aux intersections:

• Carré = rectangle ∩ diamants
• Carré = dragon quatre -cilant ∩ baice trapézoïdal
• Rectangle = Tendon Four -Ceilant ∩ Parallélogramme
• Diamants = dragon quatre-plafond ∩ trapèze
• Diamants = Tangent Four -Ceiling ∩ Parallélogramme
• Ca -on trapèze = Tendon Four -Ceiling ∩ Trapeze

Les niveaux sont divisés en différents points de vue comme suit.

1. Propriétés de l’intérieur:

2. Propriétés de symétrie:

3. Propriétés latérales:
   • Long:
   • Faire:
   • Orientation:

4. Propriétés diagonales
   • Long:
     • Les deux diagonales sont également longues: propriété nécessaire pour le même trapèze
   • Faire:
     • Coupe / touche: les deux diagonales ne se coupent pas (et ne touchent donc pas): une propriété suffisante pour le carré concave
     • Emplacement de l’intersection:
       • Une diagonale est coupée au milieu par l’autre: la propriété nécessaire pour convex dragon racilelets
       • Les deux diagonales se coupent au milieu: propriété suffisante pour un parallélogramme
   • Orientation:
     • Taille de l’angle d’orientation: Les diagonales sont à l’angle droit: propriété nécessaire pour Dragon Rivelet

5. Taille des angles:

6. Emplacement des coins:

7. Propriétés Ellipses (et cercles) associées:
   • Le plus petit cercle environnant:
     • Propriétés de la ligne de district:
       • Le plus petit cercle environnant coupe toutes les pierres angulaires du carré – alors c’est aussi un circuit tendon (= environnant): propriété nécessaire pour un diamant
     • Emplacement (le centre):
       • Le centre du cercle environnant est au milieu d’une diagonale: propriété nécessaire pour un rectangle
       • Le centre est à l’extérieur du carré: une propriété suffisante pour un carré concave
   • Umllipse minimalement excentrique (à ne pas confondre avec le Steiner-Umellipse)
     • Existence:
       • Au moins un umllipse existe: des biens suffisants et nécessaires pour la convexité d’un carré
     • Excirtrizite:
       • (Linéaire ou numérique) Excentricité = 0: propriété suffisante et nécessaire pour l’existence d’une ligne de touche. Cette ellipse est alors un cercle. C’est ce qu’on appelle le cercle ou la zone du tendon.
     • Taille des demi-haches:
       • (Longueur du premier Halbachse = longueur du deuxième rayon Halbachse =) de la zone est
         ${displaystyle {sqrt {2}}}$

         Parfois aussi grand que le rayon du district: propriété nécessaire pour un carré

   • Le plus grand cercle couché:
     • Propriétés de la ligne de district:
       • Le cercle touche tous les côtés (peut-être uniquement leurs points clés): propriété nécessaire pour un deltoïde
       • Le cercle touche tous les côtés dans l’angle plat – alors ce cercle tangent (= circuit) est mentionné: propriété nécessaire pour un deltoïde convexe
       • Le cercle ne touche pas tous les côtés: propriété nécessaire pour un carré concave

Les propriétés les plus importantes du carré spécial sont présentées dans le tableau suivant:

Un carré convexe peut être utilisé par cinq déterminations indépendantes telles que

à décrire. Un exemple de tailles non indépendantes est les quatre angles intérieurs car le quatrième angle intérieur peut être calculé à partir des trois autres et l’angle intérieur de 360 ​​°. Si les carrés non convexes sont également approuvés, il existe des combinaisons ambiguës, par ex. B. Quatre côtés et un angle intérieur, car le coin en face de l’angle donné peut être convexe ou concave.

S’il y a un carré spécial, moins de tailles sont suffisantes pour décrire sa forme:

Pour un carré convexe avec les longueurs latérales

,

,

,

, la diagonale

,

et la zone

Les inégalités suivantes s’appliquent:

${displayStyle aleq {frac {(a + c) cdot (b + d)} {4}}}$

Avec l’égalité uniquement pour les rectangles

${displayStyle Aleq {frac {a ^ {2} + b ^ {2} + c ^ {2} + d ^ {2}} {4}}}$

Avec l’égalité uniquement pour les carrés

${displayStyle aleq {frac {(a + b + c + d) ^ {2}} {16}}}$

Avec l’égalité uniquement pour les carrés

${displayStyle aleq {frac {1} {2}} cdot {sqrt {(a ^ {2} + c ^ {2}) cdot (b ^ {2} + d ^ {2})}}}$

Avec l’égalité uniquement pour les rectangles

${displayStyle aleq {frac {ecdot f} {2}}}$

Avec l’égalité uniquement si l’orthogonal diagonal

${displayStyle Aleq {frac {e ^ {2} + f ^ {2}} {4}}}$

Avec l’égalité uniquement si l’orthogonal diagonal et la même longueur sont

De la formule de Bretschneider suit avec

L’inégalité

${displayStyle Aleq {sqrt {(s-a) cdot (s-b) cdot (s-c) cdot (s-d)}}}$

Avec l’égalité uniquement pour les tiges de tendon

Zone de l’espace sur le carré irrégulier
Les lignes pointillées, le point

${displaystyle h}$

Et l’objectif

${displayStyle s_ {3}}$

et

${displayStyle s_ {4}}$

ne sont pas nécessaires à la solution alternative, ils ne servent qu’à clarifier, par exemple B. Le parallélisme de la semi-sort à la diagonale.
Animation voir ici

Pour le carré symétrique ponctuel, le parallélogramme, l’accent est mis sur le centre de symétrie, c’est-à-dire le point de coupe diagonal.

En général, vous devez faire la différence entre les coins (toutes les masse se trouvent dans les coins, chaque coin a la même masse) et la zone de terre (la masse est répartie uniformément sur la zone du carré). Dans le triangle, ces deux points focaux correspondent. De plus, il y a le bord du bord (la masse est répartie uniformément sur les bords, la masse de chaque bord est proportionnelle à sa longueur). Cependant, l’objectif du bord est rarement pris en compte. Même dans le triangle, il ne correspond pas à la zone et aux coins du coin, mais correspond au centre du centre circulaire du triangle moyen. ^[d’abord]

La zone de l’espace d’un carré irrégulier peut être construite comme suit: Vous démontez le carré par une diagonale en deux triangles et déterminez son objectif comme intersection du côté du côté. Ces deux points sont reliés par une ligne droite. Vous répétez la même chose en divisant le carré à travers l’autre diagonale. L’intersection des deux connectés droit est au centre du carré. ^[2]

L’un est une ligne lourde des deux triangles et donc aussi du carré. Ainsi, l’accent doit être mis sur cette ligne droite.

Vous obtenez les coins en reliant le centre des pages opposées. L’intersection des deux lignes de connexion est les coins. ^[2] Si un système de coordonnées cartésiennes est donné, les coordonnées des coins peuvent être trouvées

Des coordonnées des coins

calculer:

${displayStyle x_ {s} = {frac {1} {4}} cdot (x_ {a} + x_ {b} + x_ {c} + x_ {d}), quad y__ {s} = {frac {1} {4}} cdot (y_ {a} + y_ {b} + })}$

La représentation adjacente, construite de la même manière comme décrite ci-dessus, comprend également une procédure alternative. De plus, leur objectif est de traverser deux triangles

et

déterminer. Enfin, un semi-sortant

Parallèle à la diagonale

Et une demi-ligne

Parallèle à la diagonale

tiré. Ainsi, l’intersection des deux semi-sortants est au centre de la région

du carré. Cela signifie les lignes pointillées, le point

Et l’objectif

et

ne sont pas requis pour la procédure alternative.

• Une éventuelle preuve géométrique élémentaire de l’exactitude de la construction est contenue dans un carré irrégulier.

1. ↑ Hartmut Wellstein: Site Web de l’Université de Flensburg, géométrie élémentaire, Focus of the Triangle, Chapter 1.3.2, au 28 janvier 2001 ( Mémento à partir du 15 août 2010 dans Archives Internet ) consulté le 28 septembre 2017
2. ↑ ^{un b} Son Walser: 4 Points focaux sur le carré, 4.2 Focus de la zone Fig. 14. Dans: Focus pour le forum pour la promotion douée du 22 au 24 mars 2012, tu Berlin. Université Hans Walser de Bâle, Consulté le 28 septembre 2017 .