Transformation du radon – Wikipedia

Le Transformation du radon est une transformation intégrale d’une fonction dans deux variables. Il devient l’intégrale de la ligne de la fonction

${displayStyle f (x, y)}$

le long de la ligne du

${displaystyle x}$

–

${displaystyle y}$

-Bain déterminé. Pour chacun de ces lignes droites, vous pouvez avoir le radon transformé

${displayStyle RF}$

Comme projection de la fonction

${displayStyle f (x, y)}$

Introduisez-le simplement à un. La transformation du radon est liée à la transformation de Fourier et, en deux dimensions, représente une généralisation de la transformation ABEL et un cas particulier de la transformation Hough.

La transformation du radon porte le nom du mathématicien autrichien Johann Radon. Il l’a conduite en 1917 dans la publication Sur la détermination des fonctions par leurs valeurs intégrales le long d’une certaine diversité un. ^[d’abord] Une application pratique importante de cette transformation, plus précisément la retransformation, réside dans la tomographie par ordinateur pour l’acquisition d’images.

Peut être

${displayStyle fcolon mathbb {r} ^ {2} rightarrow mathbb {r}}$

régulièrement et à l’extérieur d’un cercle de rayon enfin identique à zéro

${DisplayStyle Gamma}$

Un droit à travers l’angle

${displaystyle alpha}$

à l’axe x et à leur distance

${displaystyle r}$

est défini à l’origine. Alors la transformation du radon est donnée par l’intégrale de la ligne de

${displayStyle f (x, y)}$

le long de

${DisplayStyle Gamma}$

.

${displayStyle rf (gamma) = int _ {gamma} f (x, y), mathrm {d} s}$

Droit

${DisplayStyle Gamma}$

peut être paramétré comme

${displayStyle (x (t), y (t)) = (rcos alpha + tsin alpha, rsin alpha -tcos alpha)}$

. Cela peut également être utilisé pour écrire l’intégrale de la ligne comme

${displayStyle rf (r, alpha) = int _ {- infty} ^ {infty} f (rcos alpha + tsin alpha, rsin alpha -tcos alpha), mathrm {d} t.}$

La formation de réinitialisation peut être effectuée à l’aide de la projection de dos filtrée ou par le détour de la transformation de Fourier, en tenant compte du théorème de coupe central.

Le problème du retour est un mauvais problème, ^[2] Parce que la solution n’est pas une fonction constante des données d’entrée. Afin de résoudre le problème suffisamment précisément, des techniques de régularisation ou des procédures itératives peuvent être utilisées.

Dans la tomographie, les intégrales d’une fonction sont déterminées par la ligne droite et les images sont calculées à l’aide d’une projection de radon inverse. Par exemple, dans la tomographie par ordinateur avec un rayonnement des rayons x, l’absorption du rayonnement est déterminée le long d’une ligne droite de la source de rayons x à un détecteur, c’est-à-dire l’intégrale via l’absorption. Au lieu de rayons X, d’autres rayons tels que le rayonnement gamma peuvent également être utilisés comme dans la tomographie par émission de positrons. La mesure a lieu dans toutes ces variantes pour de nombreuses lignes droites de ce type dans un niveau, dans lesquelles de nombreux détecteurs et de nombreuses positions de la source de rayonnement sont déplacés vers l’objet pour être éclairés. La transformation du radon de l’absorption du rayonnement est déterminée, bien que uniquement pour de nombreuses valeurs des deux paramètres. L’image à deux dimensions peut être obtenue à partir de ces valeurs à l’aide de la retransformation. La série de plusieurs “coupes” de ce type se traduit par une image à trois dimensions.

Les images de test sont utilisées pour évaluer les algorithmes d’imagerie, comme indiqué ci-dessous sur l’image de test Shepp Logan. L’image de test Shepp Logan représente un graphique tel qu’il se produit sous une forme similaire dans les diagnostics médicaux, un affichage de coupe simplifié à travers la tête humaine:

• Shepp-Logan-Bildsenshenz
• 

  Image originale (image de test Shepp-Logan)

• 

  Radon transformé de l’image d’origine.
  Calculé sur 180 ° en 2 ° étapes.

• 

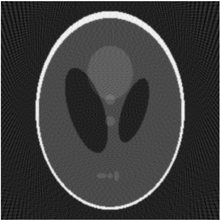
  L’image transformée du dos avec des artefacts causés par la résolution finie

1. ↑ Johann Radon: À propos de la détermination des fonctions . Dans: Rapports sur les négociations de la Royal Saxon Society of Sciences à Leipzig. Classe mathématique-physique . Groupe 69 , 1917, S. 262–277 .
2. ↑ A. K. Louis: Problèmes inverses et mal posés. Teubner, 1989 (Chap. 6.1 et 6.2)