Points fixes – Wikipedia

Un Titre de point de fixation (ou un Un point fixe ) En mathématiques est un processus numérique pour l’approximation des solutions à une équation ou un système d’équation. L’équation doit d’abord être dans une équation de point fixe, c’est-à-dire dans une équation de la forme

${DisplayStyle Varphi (x) = x}$

after-content-x4

Avec une fonction

${displaystyle varphi}$

à forme. Alors il y aura un point de départ

${displayStyle x_ {0}}$

choisi et

${DisplayStyle x_ {1} = varphi (x_ {0})}$

calculé. Le résultat est à nouveau dans la fonction

${displaystyle varphi}$

utilisé,

${DisplayStyle x_ {2} = varphi (x_ {1})}$

et ainsi de suite. Selon des exigences supplémentaires appropriées, la conséquence obtenue approche

${displayStyle x_ {0}, x_ {1}, x_ {2}, dotsc}$

une solution de

${DisplayStyle Varphi (x) = x}$

Et donc une solution au problème d’origine.

Il y a une fonction

${DisplayStyle Varphi Colon MTO M}$

Le beaucoup

${displaystyle m}$

illustré en soi, ainsi qu’un élément de départ

${displayStyle x_ {0} dans m}$

. La séquence générée par le processus de point fixe associé

${DisplayStyle (x_ {k}) _ {kin mathbb {n} _ {0}}}$

dans

${displaystyle m}$

est alors défini itérative par

${displayStyle x_ {k + 1} = varphi (x_ {k})}$

pour

${DisplayStyle kin mathbb {n} _ {0}}$

.

Quand la foule

${displaystyle m}$

Il y a un concept de convergence, on peut se demander si cet épisode contre un point fixe de

${displaystyle varphi}$

, c’est-à-dire contre un

${displaystyle x ^ {*}}$

avec

${DisplayStyle Varphi (x ^ {*}) = x ^ {*}}$

convergé. L’ensemble de points fixes de banache indique des conditions relativement générales dans lesquelles c’est:

${displaystyle m}$

un espace métrique complet, par exemple une partie terminée de la

${displayStyle Mathbb {r} ^ {n}}$

Ou une salle de Banach, et

${displaystyle varphi}$

Une contraction, alors il y a beaucoup

${displaystyle m}$

Exactement un point fixe

${displaystyle x ^ {*}}$

depuis

${displaystyle varphi}$

et la séquence générée par le processus de point fixe converge

${displayStyle x_ {0} dans m}$

contre

${displaystyle x ^ {*}}$

.

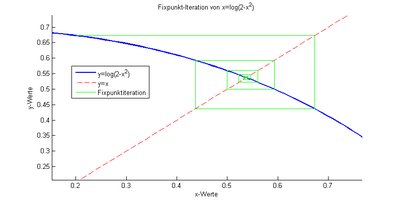
Nous recherchons la solution positive à l’équation

${displayStyle 2-x ^ {2} = e ^ {x}}$

.

L’équation de point fixe est obtenue par LogarithMing

${displayStyle ln (2-x ^ {2}) = x}$

.

Par

${DisplayStyle Varphi (x) = ln (2-x ^ {2})}$

L’intervalle, par exemple, forme la fonction d’itération donnée

${displayStyle m = [0 {,} 2; 0 {,} 7]}$

en toi et est sur

${displaystyle m}$

Une contraction (voir illustration adjacente).

À partir de la valeur de départ

${displayStyle x_ {0} = 0 {,} 2}$

Résultats pour les prochaines étapes d’itération

${displayStyle x_ {1} = varphi (x_ {0}) environ 0 {,} 6729}$

,

${displayStyle x_ {2} = varphi (x_ {1}) environ 0 {,} 4364}$

,

${displayStyle x_ {3} = varphi (x_ {2}) environ 0 {,} 5931}$

etc. Quand environ environ 20 étapes

${displayStyle x_ {20} environ 0 {,} 5373}$

Les quatre premières décimales correspondent déjà à la solution exacte.

La procédure Heron représente également un titre de point fixe. ^[d’abord] Pour

${Style de texte A> 0}$

${textStyle Varphi (x) = {frac {1} {2}} cdot gauche (x + {frac {a} {x}} droit)}$

le point fixe (positif)

${textstyle x={sqrt {a}}}$

, de sorte que

${Style de texte Varphi (x)}$

À la détermination numérique de

${Style de texte {sqrt {a}}}$

peut être utilisé.

Peut être

${displayStyle fcolon [a, b] to [a, b] sous-ensemble mathbb {r}}$

constant
Fonction de points de fixation différente avec

${displaystyle f (a)> a, f (b)$

et

${displaystyle f ‘(x) neq 1}$

pour tous

${displaystyle x}$

hors de

${displayStyle (a, b)}$

.
Ensuite, il y a exactement un point fixe

${displaystyle x ^ {*}}$

hors de

${displayStyle (a, b)}$

avec

${displayStyle f (x ^ {*}) = x ^ {*}}$

.

Preuve [ Modifier | Modifier le texte source ]]

Vous définissez

${displayStyle f (x): = f (x) -x}$

. Alors

${displayStyle f (a)> 0, f (b) <0}$

. À partir de la valeur intermédiaire, il s’ensuit qu’au moins
un zéro

${displaystyle x ^ {*} dans [a, b]}$

donner avec

${displayStyle f (x ^ {*}) = 0}$

. S’il y avait un deuxième point zéro, par exemple

${displaystyle x ^ {**}}$

, alors ça devrait être à cause de

${displayStyle f (x ^ {*}) = f (x ^ {**})}$

Selon la phrase de Roll un point

${displayStyle {check {x}}}$

du
intervalle

${displayStyle (x ^ {*}, x ^ {**})}$

donner

${displayStyle f ‘({check {x}}) = 0}$

, était

${displayStyle f ‘({check {x}}) = 1}$

Implicite en contradiction à
Hypothèse. Donc le point fixe est

${displaystyle x ^ {*}}$

clairement.

Exemple [ Modifier | Modifier le texte source ]]

Pour la fonction

${displayStyle f (x) = {frac {x ^ {3} -1} {x ^ {3} -2}}}$

s’applique à

${DisplayStyle [-1, + 1]}$

:

• 
  ${displayStyle f (-1)> 0> -1}$

  
  ${displayStyle f (+1) = 0 <1}$

  .

• 
  ${displayStyle f ‘(x) = {frac {-3x ^ {2}} {(x ^ {3} -2) ^ {2}}} neq 1}$

  pour tous

  ${displayStyle xin (-1, + 1)}$

  .

À partir de cela découle avec la phrase ci-dessus

${displaystyle f}$

dans

${DisplayStyle (-1, + 1)}$

a exactement un point fixe
((

${displayStyle x ^ {*} environ 0 {,} 4722129517}$

).

Page de construction [ Modifier | Modifier le texte source ]]

Les méthodes de fractionnement sont un cas spécial important de points fixes. À un système linéaire d’équations

${displayStyle ax = b}$

Avec un rien dans n × n -Matrice

${displaystyle a}$

et un vecteur

${displaystyle b}$

pour se former en une équation de points fixe,
Si vous démontez la matrice

${displaystyle a}$

Avec l’aide d’un rien inin n × n -Matrice

${displaystyle b}$

dans

${displayStyle a = b + (a-b)}$

.

Alors suivez

${displayStyle ax = b}$

${displayStyle bx + (a-b) x = b}$

${displayStyle rightarrow x = b ^ {- 1} b-b ^ {- 1} (a-b) x = (e-b ^ {- 1} a) x + b ^ {- 1} b}$

,

par lequel

${displaystyle e}$

la matrice unitaire.

Le système linéaire des équations

${displayStyle ax = b}$

est alors équivalent à la tâche de point fixe

${DisplayStyle x = varphi (x)}$

avec

${DisplayStyle varphi (x) = (e-b ^ {- 1} a) x + b ^ {- 1} b}$

.

Vous obtenez pour un vecteur de démarrage donné

${displayStyle x_ {0}}$

la procédure d’itération suivante pour

${displayStyle k = 0,1, ldots}$

${displayStyle x_ {k + 1} = (e-b ^ {- 1} a) x_ {k} + b ^ {- 1} b}$

,

Et le associé Iterationsmatrix Lit:

${displayStyle e-b ^ {- 1} a}$

.

convergence [ Modifier | Modifier le texte source ]]

À partir du point fixe de Banach et d’autres considérations, il s’ensuit que ces méthodes de point fixe sont exactement pour chaque vecteur de démarrage

${displayStyle x_ {0}}$

converge si le rayon spectral de la matrice d’itération

${displayStyle rho (e-b ^ {- 1} a) = max _ {i} | lambda _ {i} (e-b ^ {- 1} a) | <1}$

.

${displayStyle rho (e-b ^ {- 1} a)}$

devrait être aussi petit que possible, car cela détermine la vitesse de convergence.

Procédures spéciales [ Modifier | Modifier le texte source ]]

Les méthodes connues suivantes sont basées sur l’idée de construction ci-dessus pour résoudre les systèmes d’équations linéaires:

Remarques [ Modifier | Modifier le texte source ]]

Procédure d’itération du formulaire

${displayStyle x_ {k + 1} = mx_ {k} + v}$

, K = 0, 1, …

• linéaire , d. h. X _{K + 1} Linéaire ne s’accroche qu’à x _k un B,
• Stationnaire , d. H. M et V sont indépendants du numéro de pas de l’itération,
• seul , d. H. Seuls les derniers vecteurs d’approximation sont utilisés.

La procédure de Newton peut être considérée comme des points fixes. En général, la convergence est assurée à l’aide de l’ensemble de points fixes de Banach, la fonction considérée doit donc être une contraction, en particulier dans la zone considérée.

• Wolfgang Dahmen, Arnold Reusken: Numerics pour les ingénieurs et les scientifiques. 2e édition. Springer-Verlag, Berlin 2008, ISBN 978-3-540-76492-2.
• Martin Hermann: Mathématiques numériques, Volume 1: Problèmes algébriques . 4e édition révisée et élargie. Walter de Gruyter Verlag, Berlin et Boston 2020. ISBN 978-3-11-065665-7.

1. ↑ Transformations appropriées: zéro points et points fixes. Dans: Université de Montan Leoben. 23 février 2005, Récupéré le 27 août 2019 .