Fonction gastrationnelle – Wikipedia

Un fonction complète ou Fonction polynomiale est une fonction en mathématiques qui peut être décrite comme une somme de fonctions de puissance avec des exposants naturels. Ainsi, de telles fonctions ne peuvent être décrites qu’au moyen des opérations, de la soustraction et de la multiplication. Toutes les fonctions rationnelles sont parmi les fonctions rationnelles et, en tant que cas spéciaux, contiennent les fonctions linéaires et carrées.

Cet article traite principalement des fonctions complètes et rationnelles qui sont courantes dans les mathématiques scolaires sur les figures réelles. De plus amples informations sur les généralisations possibles du concept peuvent être trouvées dans l’article Polynome.

Une fonction rationnelle entière est une fonction réelle qui est sous la forme

${Affichestyle f (x) = a_ {n} x ^ {n} + a_ {n-1} x ^ {n-1} + dotsb + a_ {2} x ^ {2} + a_ {1} x + a_ {0} = sum _ {k = 0}} a_ {k}}}}}}} x$

Permet d’écrire, par lequel

${Displaystyle nin mathbb {n}}$

Un nombre naturel et

${displayStyle a_ {n}, a_ {n-1}, dotsc, a_ {2}, a_ {1}, a_ {0}}$

sont des nombres réels et

${displayStyle a_ {n} neq 0}$

est applicable. ^[d’abord] Le nombre

${displaystyle n}$

Enregistre la fonction, les nombres

${displayStyle a_ {n}, a_ {n-1}, dotsc, a_ {2}, a_ {1}, a_ {0}}$

sont leurs coefficients. Le coefficient

${displayStyle a_ {n}}$

est appelé coefficient de premier plan. Le résumé

${displayStyle a_ {0} x ^ {0} = a_ {0}}$

signifie absolument membre, le résumé

${displaystyle a_ {1} x}$

et

${displaystyle a_ {2} x ^ {2}}$

sont parfois appelés membres linéaires ou carrés.

De plus, la fonction réelle est également

${displayStyle f (x) = 0}$

une fonction rationnelle entière; Il est également appelé le polynôme zéro. De cette façon, tout le monde est fini Sommes de sommes de forme

${displaystyle a_ {k} x ^ {k}}$

Avec des nombres réels

${displaystyle a_ {k}}$

Toutes les fonctions rationnelles. Puisque aucune de la fonction zéro constante

${displaystyle a_ {k}}$

n’est pas nul, aucun degré n’est défini pour toute cette fonction rationnelle.

L’affichage de la fonction rationnelle entière spécifiée ici est sa forme normale. Par exemple, vous pouvez également représenter une fonction rationnelle entière en utilisant des facteurs linéaires ou en utilisant le schéma Horner.

• La fonction avec l’équation fonctionnelle
  ${displayStyle f (x) = – 2x ^ {3} + 3x ^ {2} -5x + 4}$

  est une fonction rationnelle entière de la 3e année avec les coefficients

  ${DisplayStyle -2,3, -5}$

  et

  ${Displaystyle 4}$

  .

• À la fonction
  ${displayStyle fcolon mathbb {r} à mathbb {r}, xmapsto -2x (x-1) (x + 3) ^ {2}}$

  Le fonctionnel doit d’abord être réécrit en dissolvant les supports en une somme:

${displayStyle {begin {aligné} f (x) & = – 2x (x-1) (x + 3) ^ {2} = (- 2x ^ {2} + 2x) (x ^ {2} + 6x + 9) \ & = – 2x ^ {4} -10x ^ {3} -6x ^ {2} + 18x, fin {Aligned}}}}}$

Le degré est donc 4 et les coefficients sont

${DisplayStyle -2, -10, -6,18}$

et

${DisplayStyle 0}$

.

• Avec une fonction rationnelle entière du degré
  ${DisplayStyle 5}$

  Avec les coefficients

  ${displayStyle -1,0, {sqrt {2}}, – 2pi, 0,1}$

  Le fonctionnel peut-il être écrit comme

  ${displayStyle f (x) = – x ^ {5} + {sqrt {2}} x ^ {3} -2pi x ^ {2} +1}$

  .

• Sans degré défini, il n’y a aucun polynôme
  ${displayStyle fcolon mathbb {r} à mathbb {r}, xmapsto 0}$

  , une fonction constante.

• Pour
  ${displayStyle n = 0}$

  et

  ${displayStyle a_ {0} neq 0}$

  S’il y a d’autres fonctions constantes

  ${displayStyle fcolon mathbb {r} à mathbb {r}, xmapsto a_ {0}}$

  .

• Pour
  ${displayStyle n = 1}$

  entraîner des fonctions linéaires

  ${displayStyle fcolon mathbb {r} à mathbb {r}, xmapsto a_ {1} x + a_ {0}}$

  (au lieu de

  ${displaystyle m}$

  Alors tu écris pour la pente ici

  ${displayStyle a_ {1}}$

  , et plutôt

  ${displaystyle n}$

  pour le

  ${displaystyle y}$

  SECTION SO-AXIS

  ${displayStyle a_ {0}}$

  ).

• Pour
  ${displayStyle n = 2}$

  Ariser les fonctions carrées

  ${displayStyle fcolon mathbb {r} à mathbb {r}, xmapsto a_ {2} x ^ {2} + a_ {1} x + a_ {0}}$

  (au lieu de

  ${displaystyle a, b}$

  et

  ${DisplayStyle C}$

  Alors tu écris ici

  ${displayStyle a_ {2}}$

  ,

  ${displayStyle a_ {1}}$

  et

  ${displayStyle a_ {0}}$

  ).

• Pour
  ${displayStyle n = 3}$

  entraîner des fonctions cubes

  ${displayStyle fcolon mathbb {r} à mathbb {r}, xmapsto a_ {3} x ^ {3} + a_ {2} x ^ {2} + a_ {1} x + a_ {0}}$

  .

• Pour
  ${displayStyle n = 4}$

  Parfois, on parle de fonctions quartiques.

• Est seulement
  ${displayStyle a_ {n} neq 0}$

  et tous les autres coefficients sont les mêmes

  ${DisplayStyle 0}$

  Il en résulte une fonction de puissance

  ${displayStyle fcolon mathbb {r} à mathbb {r}, xmapsto a_ {n} x ^ {n}}$

  Avec un exposant naturel.

L’addition et la multiplication de deux fonctions rationnelles entières entraînent à nouveau des fonctions complètes. Ainsi, la quantité de fonctions rationnelles entières forme une algèbre

${displayStyle Mathbb {r}}$

. Pour le degré de fonctions complètes

${displaystyle f}$

et

${displaystyle g}$

L’estimation ou l’égalité s’applique

${displayStyle deg (f + g) leq max (deg f, deg g)}$

et

${DisplayStyle you (fcdot g) = u f + u g}$

.

Décrit

${displayStyle deg f}$

le degré de

${displaystyle f}$

.

De plus, la chaîne de deux fonctions rationnelles entières est à nouveau une fonction rationnelle entière, ce qui signifie que vous obtenez à nouveau une fonction rationnelle entière si vous utilisez une fonction rationnelle entière pour la variable fonctionnelle.

• Si tous les exposants sont droits, le graphique de la fonction est anxil-symétrique
  ${displaystyle y}$

  -Axe. La fonction est alors appelée; Ça s’applique

  ${displayStyle f (-x) = f (x)}$

  .

• Si tous les exposants sont étranges, le graphique de la fonction est ponctuel symétriquement à l’origine. La fonction signifie alors également impair; Ça s’applique
  ${displayStyle f (-x) = – f (x)}$

  .

• Si les deux exposants impairs se produisent, le graphique n’a pas de symétrie simple; Cependant, il peut toujours être symétrique pour d’autres axes ou points.

Exemples:

En général, le comportement de

${displaystyle xto pm infty}$

À travers les résumés avec l’exposant le plus élevé, le comportement de

${displayStyle xto 0}$

déterminé par les résumés avec les exposants les plus bas.

croissance [ Modifier | Modifier le texte source ]]

Toutes les fonctions rationnelles peuvent être comprises comme des combinaisons linéaires de puissances. Par conséquent, ils se développent (pour des valeurs suffisamment grandes) plus lentement que toute fonction exponentielle, dont la base est supérieure à 1, quels que soient les coefficients.

Comportement pour très grand et très petit X -Valeurs [ Modifier | Modifier le texte source ]]

Toutes les fonctions rationnelles entières divergence pour

${displaystyle xto pm infty}$

. Le comportement exact dépend de la question de savoir si le diplôme n est droit ou étrange, et quel signe du coefficient principal

${displayStyle a_ {n}}$

a; Le graphique se comporte ainsi que le graphique d’une fonction de puissance avec le terme

${DisplayStyle g (x) = a_ {n} x ^ {n}}}$

. La valeur résultante de la valeur est également donnée ci-dessous

${Déplastyle Mathbb {w}}$

Dans le cas où la quantité de définition

${displayStyle Mathbb {d} = mathbb {r}}$

est.

Comportement pour les valeurs x proches de zéro [ Modifier | Modifier le texte source ]]

Toutes les fonctions rationnelles entières sont pour

${displayStyle xto 0}$

enfin. Ce qui suit s’applique plus précisément: le graphique coupe le

${displaystyle y}$

-Een axe à

${displayStyle a_ {0}}$

, la pente à ce stade est à travers

${displayStyle a_ {1}}$

donné. La tangente à l’intersection avec le

${displaystyle y}$

Donc, l’axe a toujours l’équation

${displayStyle y = a_ {1} x + a_ {0}}$

.

Exemple [ Modifier | Modifier le texte source ]]

Le graphique de la fonction

${displayStyle fcolon mathbb {r} à mathbb {r}, xmapsto -2x ^ {5} + 4x ^ {3} -3x + 1}$

courir pour

${displaystyle xto pm infty}$

Comme le graphique de la fonction

${displayStyle gcolon mathbb {r} à mathbb {r}, xmapsto -2x ^ {5}}$

, c’est-à-dire du bas à droite en bas à droite (degré

${displayStyle n = 5}$

Coefficient étrange et principal

${displayStyle a_ {5} = – 2 <0}$

). Ce qui suit s’applique aux valeurs fonctionnelles:

${displayStyle f (x) à infty}$

pour

${displayStyle xto -infty}$

et

${displayStyle f (x) à -infty}$

pour

${displayStyle xto infty}$

. Pour

${displayStyle xto 0}$

D’un autre côté, il fonctionne comme le graphique de

${displayStyle h (x) = – 3x + 1}$

, il coupe le

${displaystyle y}$

Donc axe à

${Displaystyle 1}$

et a la pente là-bas

${Displaystyle -3}$

.

Quand zéro point une fonction rationnelle entière

${displaystyle f}$

Devenez ces valeurs

${Displaystyle xi}$

Décrit pour lequel la valeur fonctionnelle est nul, c’est-à-dire l’équation

${displayStyle f (xi) = 0}$

remplir. Une fonction rationnelle entière a toujours autant de points zéro que vous ne le dites. La fonction constante

${displayStyle f (x) = 0}$

, le polynôme zéro, a un nombre infini de zéro. L’ensemble des fonctions rationnelles de grade 0, à savoir les fonctions constantes

${displayStyle f (x) = a}$

pour un

${displayStyle aneq 0}$

, en revanche, n’ont pas de points zéro, car cela correspond à leur degré.

Facteur linéaire [ Modifier | Modifier le texte source ]]

Est la fonction d’une fonction rationnelle entière comme un produit de facteurs linéaires (dont certains peuvent également se produire plusieurs fois) et peut-être une fonction rationnelle entière g donné sans points zéro, c’est-à-dire

${displayStyle f (x) = (x-x_ {1}) ^ {k_ {1}} cdot (x-x_ {2}) ^ {k_ {2}} dotsm (x-x_ {m}) ^ {k_ {m}} cdot g (x),}$

aussi

${displayStyle x_ {1}, x_ {2}, dotsc, x_ {m}}$

Les points zéro. Les nombres naturels

${displayStyle k_ {1}, k_ {2}, dotsc, k_ {m}}$

Nomme le Plusieurs fonctionnalités des positions zéro.

Exemple: la fonction

${displayStyle fcolon mathbb {r} à mathbb {r}, xmapsto -0 {,} 01cdot x ^ {3} cdot (x-2) cdot (x + 3) ^ {2} cdot (x ^ {2} +1)}$

A le point zéro à trois temps

${displayStyle x_ {1} = 0}$

, le simple point zéro

${displayStyle x_ {2} = 2}$

et le point zéro double / deux

${displayStyle x_ {3} = – 3}$

; Les facteurs

${DisplayStyle -0 {,} 01}$

et

${displaystyle x ^ {2} +1}$

peut, en revanche, pour non

${displaystyle xin mathbb {r}}$

Devenez zéro, alors ne livrez pas encore de zéro.

Le facteur linéaire d’une fonction rationnelle entière peut être déterminé, par exemple, à l’aide de la division polynomiale. L’ensemble fondamental de l’algèbre suit que chaque fonction rationnelle entière peut être décomposée en un produit à partir de facteurs linéaires via les figures complexes. Si la fonction a uniquement des coefficients réels, il s’ensuit qu’avec chaque point zéro complexe, le nombre complexe conjugué est un point zéro. Il en résulte: toute fonction rationnelle entière sur les nombres réels (à l’exception de l’ordre) peut être clairement indiqué comme un produit de termes linéaires et carrés.

La multiplication des points zéro est également directement lié aux dérivations de la fonction:

${displayStyle x_ {0}}$

Est alors exactement un

${displaystyle k}$

-filage zéro de

${displaystyle f}$

Si s’applique

${displayStyle f (x_ {0}) = f ‘(x_ {0}) = dotsb = f ^ {(k-1)} (x_ {0}) = 0}$

et

${displayStyle f ^ {(k)} (x_ {0}) neq 0}$

.

Cours du graphique aux points zéro [ Modifier | Modifier le texte source ]]

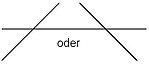
• À chaque point zéro de la diversité unstère, le graphique coupe le
  ${displaystyle x}$

  -Axe. Ainsi, les valeurs fonctionnelles modifient leur signe. Avec des points zéro simples le

  ${displaystyle x}$

  -Een -axis coupé supérieur à 0 ° à un angle. Avec chaque point zéro des Unpasters, la pente au point zéro 0 est supérieure à trois; Le graphique fonctionnel a un point de terrasse.

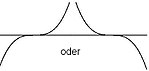
• À chaque point zéro de la diversité droite, le graphique touche le
  ${displaystyle x}$

  -Axe. Ainsi, les valeurs fonctionnelles ne modifient pas votre signe là-bas. Le graphique fonctionnel a un point extrême pour chaque point zéro de ces.

Illustration graphique:

Easy Zero	Point zéro à trois, cinq, 2k + 1 fois	Point zéro double, quatre, 2 km

Si vous prenez également en compte le comportement de

${displaystyle xto pm infty}$

, cela se traduit par l’exemple ci-dessus

${displayStyle f (x) = – 0 {,} 01x ^ {3} (x-2) (x + 3) ^ {2} (x ^ {2} +1)}$

Le graphique suivant:

Nombre de points zéro [ Modifier | Modifier le texte source ]]

Avec l’aide de la division polynomiale, vous pouvez montrer qu’une fonction rationnelle entière du degré

${displaystyle n}$

au plus

${displaystyle n}$

Peut avoir zéro point (compté plusieurs fonctionnalités).

Si vous regardez également le comportement du graphique pour

${displaystyle xto pm infty}$

, Le comportement aux sites zéro (changement de signe) et la stabilité suit également: si le degré est droit ou impair, le nombre de tous les points zéro (caractéristiques multiples) est droite ou impair. En particulier, chaque fonction rationnelle entière d’un degré inchangé a au moins un zéro.

Il existe également d’autres règles supplémentaires pour le nombre de points zéro tels que la règle de signe de Descartes et la chaîne Sturmsche.

L’ensemble fondamental de l’algèbre indique qu’une fonction rationnelle entière du degré

${displaystyle ngeq 1}$

a au moins un zéro complexe (existence pure). Puis elle a exactement

${displaystyle n}$

Zéro tache si le zéro pointe selon le leur Multiplicité Être compté. Par exemple, le zéro est

${displayStyle x = 2}$

la fonction

${displayStyle (x-2) ^ {2}}$

un double. En conséquence, toute fonction complète du degré positif peut être décomposée en un produit de facteurs linéaires.

Zéro [ Modifier | Modifier le texte source ]]

L’emplacement de tous les points zéro d’une fonction rationnelle entière du degré

${displaystyle n}$

Peut être à travers Barrières à point zéro, Dans leur calcul, évaluez uniquement les coefficients et le degré de polynôme.

Réinitialisation réelle codchrank [ Modifier | Modifier le texte source ]]

Un cas spécial important est de véritables barrières de base zéro. Un numéro

${DisplayStyle bin mathbb {r} _ {+}}$

signifie réel paquet zéro d’une fonction rationnelle entière

${displaystyle f}$

Si tous les vrais points zéro de

${displaystyle f}$

à l’intervalle

${displayStyle [-b, b]}$

poser; Il s’appelle le paquet zéro supérieur supérieur de

${displaystyle f}$

Si tous les vrais points zéro de

${displaystyle f}$

Plus petit ou égal

${displaystyle b}$

sont. Les barrières de base zéro inférieures sont expliquées de manière analogue.

Voici des exemples de véritables barrières de base zéro pour les fonctions complètes

${displayStyle f (x) = x ^ {n} + sum _ {i = 0} ^ {n-1} a_ {i} x ^ {i}}$

,

dont le coefficient principal en est un. Toute fonction rationnelle entière peut être apportée à cette forme par le biais d’une division. L’indice partiel joue pour quelques vrais corps zéro

${displayStyle n = Left {kin {0,1, dotsc, n-1} mid a_ {k} <0Right}}$

Les coefficients vraiment négatifs de

${displaystyle f}$

Un rôle spécial,

${displayStyle | n |}$

décrit leur numéro.

${displayStyle b ^ {n} geq sum _ {i = 0} ^ {n-1} | a_ {i} | b ^ {i}}$

accompli, est une véritable barrière de base zéro (telle

${displaystyle b}$

sont même des barrières pour les quantités de points zéro complexes de polynôme complexe). Les cas particuliers sont (voir également la phrase de Gerschgorin)

• • 
    ${displayStyle b = 1 + max nolimits _ {i = 0 ,, dotsc ,, n-1} | a_ {i} |}$

    et

  • 
    ${displayStyle b = max gauche (1, sum _ {i = 0} ^ {n-1} | a_ {i} | à droite)}$

    .

Barrières de base zéro complexes [ Modifier | Modifier le texte source ]]

Si vous regardez les fonctions polynomiales

${displaystyle f}$

Avec des coefficients complexes, leur domaine de définition

${displaystyle mathbb {C} }$

Si, alors il y a des cercles autour du point zéro de la figure complexe de niveau la contrepartie aux barrières de base zéro réelles, dont le rayon doit être sélectionné si grand que tout (ou en fonction de l’application même “quelques-uns”) des points zéro complexes de la fonction polynomiale sont sur le disque circulaire avec ce rayon. Un numéro

${DisplayStyle bin mathbb {r} _ {+}}$

signifie un faisceau zéro complexe de la fonction polynomiale

${displaystyle f}$

Si tous les points zéro de

${displaystyle f}$

Sur le disque circulaire autour du point zéro avec un rayon

${displaystyle b}$

Mensonge (ou autrement formulé: si la quantité de chaque point zéro est plus petite ou égale

${displaystyle b}$

est). Un résultat pour les fonctions polynomiales complexes est:

• Chaque
  ${DisplayStyle bin mathbb {r} _ {+}}$

  L’inégalité

${displayStyle | a_ {k} | b ^ {k} geq sum _ {iin {0, dotsc, n} setminus {k}} | a_ {i} | b ^ {i}}$

accompli, définit un cercle au niveau complexe avec un rayon

${displaystyle b}$

Au point zéro qui

${displaystyle k}$

Contient des points zéro complexes (conclusion du mouvement Rouché). Cette inégalité est pour

${displayStyle k = 0, n}$

Toujours résoluble, mais pas nécessaire pour chaque index

${displayStyle k = 1, dotsc, n-1}$

.

Formules de solution [ Modifier | Modifier le texte source ]]

En principe, il existe plusieurs façons de déterminer les points zéro d’une fonction rationnelle entière. Les procédures d’itération générales, telles que le processus de Newton et le Regula Falsi ou il se spécialisent dans les procédures d’itération, telles que le processus Bairstow ou le processus Weierstraß (Durand-Kerner), peuvent être utilisés d’une part à chaque fonction polynomiale, mais perdent leurs fertiles ou placés en matière de précision et de convergence.

Les équations linéaires peuvent être résolues directement par le biais de formations équivalentes. Les points zéro sont toujours faciles. Il existe des formules de solution générales pour les équations carrées, les équations cubes et les équations quartiques.

Il existe des formules de solution pour les polynomes plus élevés, à condition que ces formes spéciales aient:

${displayStyle f (x) = c_ {0} cdot x ^ {n} + c_ {1} cdot x ^ {n-1} + dotsb + c_ {1} cdot x + c_ {0}}$

,

c’est-à-dire pour le

${displayStyle i}$

-Te coefficients s’applique

${displayStyle c_ {i} = c_ {n-i}}$

; En d’autres termes, les coefficients sont symétriques. Pour ces fonctions et celles qui répondent à une légère modification de ce symbole de symétrie, la détermination zéro à l’aide de la substitution peut

${displaystyle z = x + 1 / x}$

(ou.

${displaystyle z = x-1 / x}$

) peut être réduit à une équation polynomiale dont le degré est la moitié de la taille.

• Binome Avoir la forme
  ${displayStyle f (x) = x ^ {n} + c}$

  .

Vous définissez le coefficient

${DisplayStyle C}$

En tant que vrai, c’est comme ça qu’ils sont

${displaystyle n}$

Solutions multiples du complexe

${displaystyle n}$

-Ten unité de racines:

${displayStyle x_ {k} = {sqrt [{n}] {c}} cdot exp Left ({2kpi mathrm {i} sur n} droit), quad cgeq 0}$

${displayStyle x_ {k} = {sqrt [{n}] {Vert Cververt}} cdot exp Left ({(2k + 1) pi mathrm {i} sur n} droit), quad C <0}$

,

par lequel

${displayStyle k = 0, dotsc, n-1}$

passe par.

• Si vous pouvez découvrir un point zéro à travers n’importe quelle procédure ou en l’essayant, vous pouvez déconnecter le facteur linéaire associé à l’aide d’une division polynomiale et obtenir une équation algébrique de degré inférieur. Les multiples fonctionnalités des points zéro sont simples ici en choisissant la fréquence à laquelle un point zéro sort dans la facture. Les phrases suivantes sont utiles pour trouver un point zéro en essayant:
• Fonctions polynomiques qui Juste des puissances depuis
  ${displaystyle x}$

  contenait le formulaire:

${affichestyle f (x) = c_ {n} cdot x ^ {n} + c_ {n-2} cdot x ^ {n-2} + c_ {n-4} cdot x ^ {n-4} + dotsb + c_ {4} cdot x ^ {4} + c_ {2} cdot x ^ {2} + c_ {0}$

La solution a lieu à travers la substitution

${displaystyle z = x ^ {2}}$

. Vous avez une solution pour

${Déplastyle z_ {1}}$

trouvé, il faut tenir compte que deux solutions pour elle pour

${displaystyle x}$

doivent être dérivés:

${displayStyle x_ {1} = {sqrt {z_ {1}}}}$

et

${displayStyle x_ {2} = – {sqrt {z_ {1}}}}$

• Fonctions polynomiques qui Seulement des puissances étranges depuis
  ${displaystyle x}$

  contenait le formulaire:

${displayStyle f (x) = c_ {n} cdot x ^ {n} + c_ {n-2} cdot x ^ {n-2} + dotsb + c_ {5} cdot x ^ {5} + c_ {3} cdot x ^ {3} + c_ {1} CDOT X}$

Voici évidemment un zéro du polynôme. Le polynôme est divisé par

${displaystyle x}$

puis traite comme une fonction polynomiale

${displayStyle (n-1)}$

-Le degré qui n’est que les puissances de

${displaystyle x}$

Contient.

Fonction de dérivation [ Modifier | Modifier le texte source ]]

Les fonctions rationnelles entières sont entièrement

${displayStyle Mathbb {r}}$

constamment différencié. Fonctions qui partout

${displayStyle Mathbb {r}}$

ou partout

${displaystyle mathbb {C} }$

Peut être différencié, des fonctions entières chaudes. La fonction de dérivation peut être déterminée à l’aide du facteur, des sommes et de la règle de puissance. Cela vous donne la fonction avec le règlement

${displayStyle f (x) = sum _ {k = 0} ^ {n} a_ {k} x ^ {k}}$

La fonction de dérivation

$m sovet ylext;) umum em yo moy myo kom kom m kroom mjoy mjoy mjoys$

.

Intégabilité et fonction régulière [ Modifier | Modifier le texte source ]]

Toute fonction complète rationnelle peut être intégrée sur un intervalle compact. De plus, chaque fonction rationnelle entière a une fonction régulière. Cela peut être explicitement spécifié avec les règles intégrales habituelles. Ça s’applique:

${displayStyle int {bigg (} sum _ {k = 0} ^ {n} a_ {k} x ^ {k} {bigg)} mathrm {d} x = sum _ {k = 0} ^ {n} int a_ {k} x ^ {k} mathrm {d} x = sum _ _ _} {a_ {k}} {k + 1}} x ^ {k + 1} + c,}$

par lequel

${displaystyle cin Mathbb {r}}$

Toute constante est.

Exemples [ Modifier | Modifier le texte source ]]

Pour la fonction avec le terme

${displayStyle f (x) = 2x ^ {3} -4x ^ {2} + 5x-1}$

la fonction de dérivation avec le terme

${displayStyle {begin {aligné} f ‘(x) & = (2x ^ {3} -4x ^ {2} + 5x-1)’ \ & = (2x ^ {3}) ‘- (4x ^ {2})’ + (5x) ‘- 1’ \ & = 2 (x ^ {3}) ‘- 4 (x ^} x ^ {0}) ‘\ & = 2cdot 3x ^ {2} -4cdot 2x + 5cdot 1x ^ {0} -1cdot 0 \ & = 6x ^ {2} -8x + 5end {aligné}}}$

Dans ce cas, vous obtenez pour les fonctions régulières

${displayStyle int (2x ^ {3} -4x ^ {2} + 5x-1) mathrm {d} x = {frac {1} {2}} x ^ {4} – {frac {4} {3}} x ^ {3} + {frac {5} {2} {{2} – x + c, 5}} {2}} x ^ {2} – }.}$

Voir également dans la discussion sur la courbe de l’article La section sur des points extrêmes.

Pour déterminer les points extrêmes, les lieux avec une tangente horizontale, c’est-à-dire les points zéro de la première dérivée, doivent d’abord être calculés. La première dérivation est à nouveau une fonction rationnelle entière, mais à partir du degré

${displaystyle n-1}$

; Les mêmes méthodes peuvent donc être utilisées comme dans le calcul de la position zéro.

Règles générales [ Modifier | Modifier le texte source ]]

• Si la fonction elle-même a un point zéro de droite, votre graphique a un point extrême là-bas (voir ci-dessus à zéro point).

• Si le premier dérivé change à un moment donné votre signe de – après +, il y a une position minimale; Il passe de + à – donc il y a un point maximum; Si le signe ne change pas, il n’y a pas de point extrême (mais un point de terrasse).

• Si la deuxième dérivation est positive ou négative à un point nul de la première dérivée, la première dérivée modifie votre signe de – selon + (position minimale) ou de + à – (position maximale). Si le deuxième dérivé est nul, il peut toujours être un point extrême à ce stade, mais il peut également y avoir un point de terrasse. Différents fonds de la deuxième dérivée sont alors nécessaires pour se différencier.

• Si un point zéro de la première dérivation est une diversité étrange, la fonction a même un point extrême là-bas; Si, en revanche, c’est en grande diversité, la fonction a un point de terrasse à ce stade.

Nombre [ Modifier | Modifier le texte source ]]

De la phrase sur le nombre de points zéro d’une fonction rationnelle entière suit qu’une fonction rationnelle entière du degré

${displaystyle n}$

au plus

${displaystyle n-1}$

Peut avoir des points extrêmes.

Si vous regardez également le comportement du graphique pour

${displaystyle xto pm infty}$

Et le comportement aux points zéro (changement de signe) suit également: si le degré est droit ou impair, le nombre total de points extrêmes est impair ou droit.

En particulier, chaque fonction rationnelle entière du degré droit a un minimum ou un maximum absolu (selon que le coefficient principal

${displayStyle a_ {n}}$

est positif ou négatif).

Voir également dans la discussion sur la courbe de l’article La section via des tournants.

Pour déterminer les points tournants, les points zéro du deuxième dérivé, les points plats So-appelés, doivent d’abord être calculés. Le deuxième dérivé est à nouveau une fonction rationnelle entière, mais à partir du degré

${displaystyle n-2}$

; Les mêmes méthodes peuvent donc être utilisées comme dans le calcul de la position zéro.

Règles générales [ Modifier | Modifier le texte source ]]

• Si la fonction elle-même a une unité nul dans de nombreux cas supérieure à trois, votre graphique a un point de terrasse là-bas, y compris un tournant (voir ci-dessus à zéro point).

• Si le deuxième dérivé modifie votre signe à un moment donné, il y a un tournant là-bas.

• Si le troisième dérivé est beaucoup zéro à un zéro de la deuxième dérivation, le deuxième dérivé modifie votre signe (tournant). Si le troisième dérivé est zéro, un tournant peut toujours être à ce stade. Différents fonds de la troisième dérivation sont nécessaires pour se différencier.

• Si un point zéro de la deuxième dérivation est en grande diversité, la fonction y a même elle-même Non Tournant; D’un autre côté, si le point zéro de la première dérivation a une diversité étrange, la fonction y a même un tournant. Si la première dérivée est également nulle à ce stade, le graphique de la fonction a un point de terrasse là-bas.

• Ce qui suit s’applique en particulier aux fonctions du troisième degré:
  • Les hauts et les bas (si disponibles) sont toujours symétriques au tournant (cela suit, car les graphiques des fonctions du troisième degré sont toujours symétriques à leur tournant, voir ci-dessus).
  • Si la fonction elle-même a trois points zéro réels (pas nécessairement différents), le tournant se traduit comme sa moyenne, pondéré avec le multiple. (Si, en revanche, il n’y a qu’un véritable point zéro, les points zéro complexes doivent également être pris en compte en matière de formation.)

Nombre [ Modifier | Modifier le texte source ]]

De la phrase sur le nombre de points zéro d’une fonction rationnelle entière suit qu’une fonction rationnelle entière du degré

${displaystyle n}$

au plus

${displaystyle n-2}$

Peut avoir des points tournants.

Si vous regardez également le comportement du graphique pour

${displaystyle xto pm infty}$

Et le comportement aux positions zéro (changement de signe) suit également: si le degré est droit ou impair, le nombre total de points tournants est droit ou impair.

En particulier, chaque fonction rationnelle entière d’un degré inconditionnel plus grand Drei a au moins un tournant.

Un problème est souvent à résoudre: il y a certains points et éventuellement des conditions supplémentaires (telles que les gradients dans ces points), et une fonction rationnelle complète est recherchée, dont le graphique traverse ces points et, si nécessaire, remplit les conditions supplémentaires. Afin de trouver toute cette fonction rationnelle, vous avez d’abord configuré la fonction fonctionnelle sous la forme générale (le degré est donné directement ou devez être déterminé à partir de l’autre information donnée), peut former les dérivations nécessaires de la fonction dans cette forme générale, puis utiliser les conditions données. Cela conduit à un système linéaire d’équations pour les coefficients de la fonction; C’est ce qu’on appelle à la place

${displayStyle a_ {n}}$

,

${displaystyle a_ {n-1}}$

etc. surtout ici

${displaystyle a, b}$

etc. En desserrant ce système d’équations, vous obtenez le terme de la fonction que vous recherchez.

Exemple: nous recherchons une fonction complète aussi faible que possible, dont le graphique est symétrique à

${displaystyle y}$

-Chle est et dans le tournant

${Déplastyle w (1 | 3)}$

a incliné 2.

• Puisque le graphique symétriquement
  ${displaystyle y}$

  -Een axe doit être, le degré doit être et le fonctionnel ne peut contenir que des exposants.

• Puisqu’il devrait y avoir un tournant, le degré ne peut pas être 2 (une fonction du deuxième degré n’a pas de tournant); Le degré le plus bas possible est 4.
• Le fonctionnel sous la forme la plus générale est:

${displayStyle f (x) = ax ^ {4} + bx ^ {2} + c}$

• Puisqu’il est question d’un tournant ici, vous avez besoin de deux dérivations:

${DisplayStyle f ‘(x) = 4ax ^ {3} + 2bx}$

${displayStyle f ” (x) = 12ax ^ {2} + 2b}$

• Le graphique passe par le point
  ${displayStyle in}$

  , donc s’applique (

  ${displaystyle x}$

  – et

  ${displaystyle y}$

  -Koordinated in

  ${displaystyle f}$

  insérer)

${displayStyle 3 = acdot 1 ^ {4} + bcdot 1 ^ {2} + c}$

• Le graphique a la pente 2 là-bas, donc s’applique (
  ${displaystyle x}$

  -Coordinate et pente dans

  ${displaystyle f ‘}$

  insérer)

${displayStyle 2 = 4ACDOT 1 ^ {3} + 2bcdot 1}$

• Le point
  ${displayStyle in}$

  est un tournant, donc s’applique (

  ${displaystyle f ”}$

  Doit être 0 au tournant)

${displayStyle 0 = 12ACDOT 1 ^ {2} + 2b}$

• Dans l’ensemble, le système linéaire des résultats des équations

${displaystyle a + b + c = 3}$

${displaystyle 4a + 2b = 2}$

${displaystyle 12a + 2b = 0}$

• Loset Ce système de résultats d’équations
  ${displayStyle a = -0 {,} 25 ;; b = 1 {,} 5 ;; c = 1 {,} 75}$

  . Le terme de la fonction que je recherchais est:

${displayStyle f (x) = – 0 {,} 25x ^ {4} +1 {,} 5x ^ {2} +1 {,} 75}$

• De nombreuses courbes survenant dans la nature et la technologie peuvent être décrites relativement bien par des fonctions complètes, telles que des formations de terrain, des sauts de ski ou des flexions sur les poutres.
• Les fonctions rationnelles du mouette apparaissent souvent dans les applications géométriques. Exemples:
• Les tarifs fiscaux sont souvent décrits par des fonctions complètes. ^[2]
• Dans les applications économiques, la fonction des revenus est souvent une fonction rationnelle complète du troisième degré.
• Étant donné que les fonctions rationnelles complètes sont particulièrement simples, les fonctions souvent plus compliquées sont approximées par la série complète (voir la série Taylor et le taux d’approximation de Weierstraß). Cette procédure est utilisée en particulier dans l’analyse et la numérique. Alternativement, il existe également des situations dans lesquelles un nombre fini de valeurs fonctionnelles est spécifié et une fonction est recherchée qui traverse ces points. L’interpolation polynomiale peut être utilisée pour cela. De plus, une quantité finie de valeurs fonctionnelles peut également être interpréée par la pièce au moyen de fonctions complètes. Cette procédure est appelée interpolation divisée. Si vous souhaitez évaluer une fonction rationnelle entière à un point efficace numériquement (optimisée pour l’ordinateur), le schéma Horner peut être utilisé.

• H. Schneider, G. Stein: Mathématiques 11 et Mathématiques 12: Analyse Pour les instructions de formation non technique du collège technique.
• R. Schöwe, J. Knapp, R. Borgmann: Analyse: direction commerciale et économique Pour le collège technique.

1. ↑ Fonction complète . Dans: Guido Walz (éd.): Lexique des mathématiques . 1ère édition. Spectrum Akademischer Verlag, Mannheim / Heidelberg 2000, ISBN 3-8274-0439-8.
2. ↑ Pdf. ( Mémento à partir du 18 octobre 2015 Archives Internet ).