Distribution binomiale – Wikipedia

Distribution binomiale
Distribution de probabilité
Fonction de distribution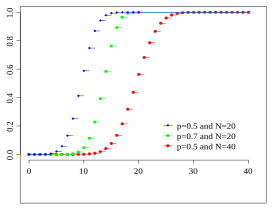
Paramètre	${Displaystyle nin mathbb {n} ^ {+}}$ , ${Pin d’affichage [0,1]}$ after-content-x4
transporteur	${displayStyle kin {0, dotsc, n}}$
Fonction de probabilité	${DisplayStyle Text Style {n Choisissez K}, p ^ {k} (1-p) ^ {n-k}}$
Fonction de distribution	${displayStyle i_ {1-p} (n-lfloor krfloor, 1 + lfloor krfloor)}$
Valeur d’attente	${DisplayStyle NP}$
Médian	je. A. Pas de formule fermée, voir ci-dessous
Modus	${displayStyle lfloor (n + 1) prfloor}$ ou after-content-x4 ${displayStyle lfloor (n + 1) p-1rfloor}$
Variance	${DisplayStyle NP (1-P)}$
Courbé	${displayStyle {frac {1-2p} {sqrt {np (1-p)}}}}$
Courbure	${displayStyle 3+ {frac {1-6p (1-p)} {np (1-p)}}}$
Entropie	${displayStyle {frac {1} {2}} log _ {2} {big (} 2pi mathrm {e}, np (1-p) {big)}}$ ${displayStyle + {mathcal {o}} gauche ({frac {1} {n}} droit)}$
Fonction de génération de moment	${displayStyle gauche (1-p + pmAtHrm {e} ^ {t} droit) ^ {n}}$
Fonction caractéristique	${DisplayStyle gauche (1-p + pmathrm {e} ^ {Mathrm {i} t} droit) ^ {n}}$

Le Distribution binomiale (aussi: Distribution binominale ) est l’une des distributions de probabilité discrètes les plus importantes.

Il décrit le nombre de succès dans une série d’expériences similaires et indépendantes, chacune ayant exactement deux résultats possibles (“succès” ou “échec”). Ces séries de tests sont également appelées processus de Bernoulli.

Est

${displaystyle p}$

La probabilité de succès un Tentative et

${displaystyle n}$

Le nombre d’expériences, alors fait référence à

${Displaystyle b (kmid p, n)}$

(aussi

${displayStyle b_ {n, p} (k)}$

,

${displaystyle b (n, p, k)}$

^[d’abord] ou

${displaystyle b (n; p; k)}$

^[2] ) la probabilité de exactement

${displaystyle k}$

Pour réussir (voir la définition de la section).

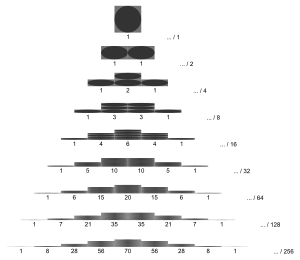
La distribution binomiale et l’expérience de Bernoulli peuvent être illustrées à l’aide du conseil d’administration de Galton. Il s’agit d’un appareil mécanique dans lequel vous jetez des balles. Ceux-ci tombent alors accidentellement dans l’un des nombreux sujets, avec la division de la distribution binomiale. Selon la construction, il existe différents paramètres

${displaystyle n}$

et

${displaystyle p}$

possible.

Bien que la distribution binomiale ait été connue bien avant, le terme a été utilisé pour la première fois en 1911 dans un livre de George Udny Yule. ^[3]

Fonction de probabilité, fonction de distribution (cumulée), propriétés [ Modifier | Modifier le texte source ]]

La distribution discrète de la probabilité avec la fonction de probabilité

${displayStyle b (kmid p, n) = {begin {cas} {binom {n} {k}} p ^ {k} (1-p) ^ {n-k} & {text {chutes}} quad kin gauche {0,1, terr$

signifie que Distribution binomiale Aux paramètres

${displaystyle n}$

(Nombre d’expériences) et

${DisplayStyle Pin à gauche [0,1Right]}$

(le Succès ou Probabilité ).

Un avis: Avec cette formule, la convention est

${DisplayStyle 0 ^ {0}: = 1}$

appliqué (voir zéro zéro élevé).

La formule ci-dessus peut être comprise comme suit: nous avons besoin d’un total de

${displaystyle n}$

Essayer exactement

${displaystyle k}$

Succès de la probabilité

${displaystyle p ^ {k}}$

et donc ont exactement

${displaystyle n-k}$

Échecs de la probabilité

${displayStyle (1-p) ^ {n-k}}$

. Cependant, tout le monde peut

${displaystyle k}$

Succès dans chacun des

${displaystyle n}$

Des expériences apparaissent pour que nous soyons toujours avec le nombre

${DisplayStyle {tbinu {n} {k}}}}}$

le

${displaystyle k}$

-Ément Sous-coseaux d’un

${displaystyle n}$

-Ément Multipliez beaucoup. Parce qu’il y a autant d’options de tout le monde

${displaystyle n}$

Essaie le

${displaystyle k}$

pour sélectionner réussi.

La probabilité de succès

${displaystyle p}$

Probabilité par défaut complémentaire

${displayStyle 1-P}$

est souvent avec

${displayStyle Q}$

abrégé.

Si nécessaire pour une distribution de probabilité, les probabilités pour toutes les valeurs possibles doivent

${displaystyle k}$

Pour ajouter 1. Cela résulte du taux d’enseignement binomien comme suit:

$mm Slave Slext ou Alyyal mâle m kal hyo syma hy huple huperkerk) Mertuber) Mertubate 10-4$

Un après

${displayStyle b (cdot mid p, n)}$

Taille aléatoire distribuée

${displaystyle x}$

Cela signifie en conséquence binomial distribué Avec les paramètres

${displaystyle n}$

et

${displaystyle p}$

ainsi que la fonction de distribution

${displayStyle f_ {x} (x) = opératorname {p} (xleq x) = sum _ {k = 0} ^ {lfloor xrfloor} {binom {n} {k}} p ^ {k} (1-p) ^ {n-k}}$

,

par lequel

${displaystyle lfloor xrfloor}$

La fonction d’arrondi mentionnée.

D’autres orthographes courantes de la distribution binomiale cumulée sont

${displayStyle f (kmid p, n)}$

,

${displaystyle f (n, p, k)}$

^[4] et

${displayStyle f (n; p; k)}$

. ^[5]

La dérivation comme une probabilité de Laplace [ Modifier | Modifier le texte source ]]

Schéma expérimental: contient une urne

${displaystyle n}$

Les balles sont d’eux

${displaystyle m}$

noir et

${displaystyle n-m}$

blanc.
La probabilite

${displaystyle p}$

Tirer une balle noire est ainsi

${displayStyle p = {frac {m} {n}}}$

.
Il y en aura un aléatoire après l’autre

${displaystyle n}$

Balles retirées, leur couleur déterminée et recouverte à nouveau.

Nous calculons le nombre d’options dans lesquelles

${displaystyle k}$

Trouver des boules noires, et à partir de celle-ci Probabilité de Laplace (“Nombre d’options pour l’événement, divisé par le nombre total d’options (également)”).

Avec chacun des

${displaystyle n}$

Il y a des tirages

${displaystyle n}$

Opportunités, donc dans l’ensemble

${displaystyle N^{n}}$

Possibilités pour la sélection des balles. Si précisément

${displaystyle k}$

ce

${displaystyle n}$

Les balles sont noires, doivent être précises

${displaystyle k}$

le

${displaystyle n}$

Tirez une balle noire. Il y a pour chaque balle noire

${displaystyle m}$

Opportunités, et pour chaque balle blanche

${displaystyle n-m}$

Possibilités.
Le

${displaystyle k}$

Les boules noires peuvent toujours être sur

${DisplayStyle {tbinu {n} {k}}}}}$

Façons possibles sur le

${displaystyle n}$

Les tirages sont distribués, donc il y a

${DisplayStyle {binom {n} {k}} m ^ {k} (n-m) ^ {n-k}}}$

Cas qui exactement

${displaystyle k}$

Les balles noires ont été sélectionnées. La probabilite

${displayStyle p_ {k}}$

, sous

${displaystyle n}$

Boules exactement

${displaystyle k}$

Donc trouver les Noirs est

${displayStyle {begin {aligned} p_ {k} & = {binom {n} {k}} {frac {m ^ {k} (n-m) ^ {n-k}} {n ^ {n}}} \ & = {binom {n} {k}}} ^ gauche ({m}} {K}}} ^ Left ({m}} {K} ée {k} Left ({frac {n-m} {n}} droit) ^ {n-k} \ & = {binom {n} {k}} p ^ {k} (1-p) ^ {n-k} .end {aligné}}}}$

Cube de jeu [ Modifier | Modifier le texte source ]]

La probabilité de rouler un 6 avec un cube de jeu normal est

${displayStyle p = {tfrac {1} {6}}}$

. La probabilite

${displayStyle Q}$

que ce n’est pas le cas est

${displayStyle q = 1-p = {tfrac {5} {6}}}$

. Supposons que vous rouliez 10 fois (

${displayStyle n = 10}$

), alors la probabilité qu’un 6 ne soit jamais roulé,

${displayStyle q ^ {10} = (1-p) ^ {10} = Left ({tfrac {5} {6}} droit) ^ {10} = {tfrac {9765625} {60466176}} Envient 0 {,} 162}$

. La probabilité qu’un 6 soit roulé exactement deux fois

${displayStyle {binom {10} {2}} Left ({tfrac {1} {6}} droit) ^ {2} Left ({tfrac {5} {6}} droit) ^ {8}}$

. En général, la probabilité

${displaystyle k}$

-Sument un nombre roul

${DisplayStyle (0leq kleq 10)}$

, à travers la distribution binomiale

${displayStyle b_ {10, {tfrac {1} {6}}} (k)}$

décrit.

Souvent, le processus décrit par la distribution binomiale est également illustré par un modèle d’urne si appelé. Dans une urne, z. B. 6 balles, 1 d’entre eux blancs, les autres noirs. Maintenant, atteignez l’urne 10 fois, sortez une balle, notez leur couleur et couvrez à nouveau le ballon. Dans une interprétation spéciale de ce processus, tirer une balle blanche est comme événement positif Avec la probabilité

${displaystyle p}$

compris, tirant une balle non blanche comme événement négatif . Les probabilités sont tout aussi distribuées que dans l’exemple avec le cube de jeu.

tissu de monnaie [ Modifier | Modifier le texte source ]]

Une pièce est lancée 7 fois. Lorsque la variable aléatoire discrète

${displaystyle x}$

Le nombre de portées comptes, avec laquelle le “nombre” est lancé

${displaystyle x}$

La distribution binomiale

${displaystyle B(kmid {tfrac {1}{2}},7)={begin{cases}{binom {7}{k}}({tfrac {1}{2}})^{k}(1-{tfrac {1}{2}})^{7-k}&{text{falls}}quad kin left{0,1,2,3,4,5,6,7right},\0&{text{sonst.}}end{cases}}}$

Les valeurs et leurs probabilités peuvent être résumées dans le tableau suivant:

La valeur des attentes est

${displayStyle {couleur {brickred} mu} = np = 7cdot {frac {1} {2}} = {couleur {brickred} 3 {,} 5}}$

.

La variance est donc donnée par

${displayStyle {begin {aligned} Sigma ^ {2} & = sum _ {i = 0} ^ {7} (x_ {i} – {Color {Brickred} mu}) ^ {2} p_ {i} = (0- {Color {Brickred} 3 {,} 5}) ^ {2} CD {Frac 8}} + (1- {couleur {brickred} 3 {,} 5}) ^ {2} CDOT {frac {7} {128}} + (2- {Color {Brickred} 3 {,} 5}) ^ {2} CDOT {Brick {21} {128}} + (3- {Color {Brick} 3 {} {} + (3 5}) ^ {2} cdot {frac {35} {128}} \ & quad + (4- {couleur {brickred} 3 {,} 5}) ^ {2} cdot {frac {35} {128}} + (5- {colore {brickred} 3 {,} 5}) } {128}} +; } = 1 {,} 75end {aligné}}}$

Avec l’ensemble de décalage, vous obtenez également la même valeur pour la variance:

${displayStyle Sigma ^ {2} = Left (sum _ {i = 0} ^ {7} x_ {i} ^ {2} p_ {i} droit) -left (sum _ {i = 0} ^ {7} x_ {i} p_ {i} à droite) ^ {2} = 0 ^ {2} } + 1 ^ {2} cdot {frac {7} {128}} + 2 ^ {2} CDOT {frac {21} {128}} + 3 ^ {2} CDOT {frac {35} {128}} + 4 ^ {2} CDOT {Frac {35} {128} {frac {21} {128}} + 6 ^ {2} cdot {frac {7} {128}} + 7 ^ {2} CDOT {frac {1} {128}} – {Color {Brickred} 3 {,} 5} ^ {2} = 1 {,} 75}$

.

Il en résulte l’écart type:

${displayStyle Sigma = {Sqrt {Sigma ^ {2}}} = {Sqrt {1 {,} 75}} Environ 1 {,} 323}$

.

symétrie [ Modifier | Modifier le texte source ]]

• La distribution binomiale est dans les cas spéciaux
  ${displayStyle p = 0}$

  ,

  ${displayStyle p = 0 {,} 5}$

  et

  ${displayStyle p = 1}$

  symétrique et autrement asymétrique.

• La distribution binomiale a la propriété
  ${DisplayStyle b (k | p, n) = b (n-k | 1-p, n).}$

  

Valeur d’attente [ Modifier | Modifier le texte source ]]

La distribution binomiale a la valeur d’attente

${DisplayStyle NP}$

.

Preuve

La valeur des attentes

${displaystyle mu}$

Calculer directement à partir de la définition

${displayStyle mu = sum _ {i = 1} ^ {n} x_ {i} p_ {i}}$

Et le taux d’enseignement binomique aussi

${displayStyle {begin {aligné} mu & = sum _ {k = 0} ^ {n} k {binom {n} {k}} p ^ {k} (1-p) ^ {n-k} \ & = npsum _ {k = 0} ^ {n} k {frac {(n-1)! gens {binom {n-1} {k-1}} p ^ {k-1} (1-p) ^ {(n-1) – (k-1)} \ & = npsum _ {ell = 0} ^ {n-1} {binom {n-1} {ell}} p ^ {ell} (1-p) ^ {(n-1) – : = k-1 \ & = npsum _ {ell = 0} ^ {m} {binom {m} {ell}} p ^ {ell} (1-p) ^ {m-ell} qquad {text {mit}} m: = n-1 \ & = npleft (p + gauche (1-pright) {aligné}}}$

Alternativement, vous pouvez en utiliser un

${displayStyle b (cdot mid p, n)}$

-Révacte aléatoire distribué

${displaystyle x}$

Comme une somme de

${displaystyle n}$

Bernoulli indépendant distribué des variables aléatoires

${displayStyle x_ {i}}$

avec

${displayStyle OperatorName {e} (x_ {i}) = p}$

peut être écrit. Suit ensuite avec la linéarité de la valeur des attentes

${DisplayStyle operatorname {e} (x) = opératalName {e} (x_ {1} + dotsb + x_ {n}) = opératorname {e} (x_ {1}) + opératorme {e} (x_ {n}) = np.})$

Alternativement, vous pouvez également fournir la preuve suivante à l’aide du taux d’enseignement binomien: si vous différenciez l’équation

$MMS Sleple (Affide?$

Les deux côtés après

${displaystyle a}$

, remis

$MMS Slepent$

,

aussi

$MMS Sleples in Sleles à Pegu-tu-tal maman Móe Em Kalu Halle Horle Male Mad Houge Mékébe comme Maluubal Salubal Salm Hmbɔ.$

.

Avec

${displayStyle a = p}$

et

${displayStyle b = 1-p}$

suit le résultat souhaité.

Variance [ Modifier | Modifier le texte source ]]

La distribution binomiale a la variance

${DisplayStyle NPQ}$

avec

${displayStyle q = 1-p}$

.

Preuve

C’est

${displaystyle x}$

un

${displayStyle b (n, p)}$

-Révance aléatoire distribuée. La variance est déterminée directement à partir du taux de décalage

${displayStyle operatorname {var} (x) = opératorname {e} gauche (x ^ {2} droit) -left (Operatorname {e} Left (xRight) droite) ^ {2}}$

pour

${displayStyle {begin {aligned} opératorname {var} (x) & = sum _ {k = 0} ^ {n} k ^ {2} cdot p (x = k) – (np) ^ {2} \ & = sum _ {k = 0} ^ {n} k ^ {2} cdot {n. k} -n ^ {2} p ^ {2} \ & = {annuler {n ^ {2} p ^ {2}}} – np ^ {2} + np {Cance$

Ou alternativement à partir de l’équation de Benaymé, appliquée à la variance des variables aléatoires indépendantes si l’on prend en compte les processus individuels identiques

${displayStyle x_ {i}}$

la distribution de Bernoulli avec

${displayStyle OperatorName {var} (x_ {i}) = p (1-p) = pq}$

se rencontrer aussi

${displayStyle operatorname {var} (x) = operatorname {var} (x_ {1} + dotsb + x_ {n}) = opératorname {var} (x_ {1}) + dotsb + operatorname {var} (x_ {n}) = nperatorname {var} (x_ {1}) = nPleft) pq.}$

La deuxième égalité s’applique parce que les expériences individuelles sont indépendantes, de sorte que les variables individuelles sont incorporées.

Coefficient de variation [ Modifier | Modifier le texte source ]]

Le coefficient de variation est obtenu à partir de la valeur d’attente et de la variance

${displayStyle OperatorName {vark} (x) = {sqrt {frac {1-p} {np}}}.}$

Courbé [ Modifier | Modifier le texte source ]]

Le tordu se pose

${displayStyle operatorname {v} (x) = {frac {1-2p} {sqrt {np (1-p)}}}.}$

Courbure [ Modifier | Modifier le texte source ]]

La courbure peut également être affichée fermée comme

${displayStyle beta _ {2} = 3 + {frac {1-6pq} {npq}}.}$

Aussi l’excès

${displayStyle gamma _ {2} = {frac {1-6pq} {npq}}.}$

Modus [ Modifier | Modifier le texte source ]]

Le mode, c’est-à-dire la valeur avec la probabilité maximale, est pour

${displaystyle p <1}$

même

${displayStyle k = lfloor np + prfloor}$

et pour

${displayStyle p = 1}$

même

${displaystyle n}$

. Chutes

${DisplayStyle NP + P}$

est un nombre naturel

${displayStyle k = np + p-1}$

Aussi un mode. Si la valeur des attentes est un nombre naturel, la valeur d’attente est égale au mode.

Preuve

Être sans restriction

${DisplayStyle 0$

. Nous regardons le quotient

${displayStyle alpha _ {k}: = {frac {b (k + 1mid p, n)} {b (kmid p, n)}} = {frac {, {frac {n!} {(k + 1)! (n-k-1)!},} {frac {n! ac {p ^ {k + 1} (1-p) ^ {n-k-1}} {p ^ {k} (1-p) ^ {n-k}}} = {frac {n-k} {k + 1}} cdot {frac {p} {1-p}}}$

.

S’applique maintenant

${displaystyle alpha _ {k}> 1}$

${displaystyle k$

et

${displaystyle alpha _ {k} <1}$

, chutes

${displaystyle k> np + p-1}$

${displayStyle {begin {aligned} k> (n + 1) p-1Rightarrow alpha _ {k} <1RightArrow b (k + 1mid p, n) 1Rightarrow b (k + 1mid p, n)> b (kmid p, n) end {aligné}}}$

${Displaystyle np + p-1in mathbb {n}}}$

Le quotient a-t-il la valeur 1, i. H.

${displayStyle b (np + p-1mid n, p) = b (np + pMid n, p)}$

.

Médian [ Modifier | Modifier le texte source ]]

Il n’est pas possible de spécifier une formule générale pour la médiane de la distribution binomiale. Par conséquent, différents cas doivent être pris en compte qui fournissent une médiane appropriée:

• Est
  ${DisplayStyle NP}$

  Un nombre naturel, alors la valeur des attentes, la médiane et le mode sont d’accord et sont les mêmes

  ${DisplayStyle NP}$

  . ^{[6] [7]}

• Une médiane
  ${displaystyle m}$

  Est dans l’intervalle

  ${displaystyle lfloor nprfloor leq mleq lceil nprceil}$

  . ^[8] Décrire ici

  ${displaystyle lfloor cdot rfloor}$

  La fonction d’arrondi et

  ${displaystyle lceil cdot rceil}$

  La fonction d’arrondi.

• Une médiane
  ${displaystyle m}$

  Je ne peux pas trop différer de la valeur des attentes:

  ${displayStyle | m-np | leq min {ln 2, max {p, 1-p}}}$

  . ^[9]

• La médiane est claire et a raison avec
  ${displayStyle m =}$

  rond

  ${displayStyle (np)}$

  d’accord si l’un ou l’autre

  ${DisplayStyle Elder 1-LN 2}$

  ou

  ${displaystyle pgeq ln 2}$

  ou

  ${displayStyle | m-np | leq min {p, 1-p}}$

  (sauf quand

  ${displayStyle p = 1/2}$

  et

  ${displaystyle n}$

  est juste). ^{[8] [9]}

• Est
  ${displayStyle p = 1/2}$

  et

  ${displaystyle n}$

  Bizarre, tout est aussi

  ${displaystyle m}$

  à l’intervalle

  ${displayStyle 1/2 (n-1) leq mleq 1/2 (n + 1)}$

  Une médiane de la distribution binomiale avec les paramètres

  ${displaystyle p}$

  et

  ${displaystyle n}$

  . Est

  ${displayStyle p = 1/2}$

  et

  ${displaystyle n}$

  droit, aussi

  ${displayStyle m = n / 2}$

  La médiane claire.

Cumulateur [ Modifier | Modifier le texte source ]]

Analogue à la distribution de Bernoulli, la fonction générateurs de cumulator est

${displayStyle g_ {x} (t) = nln (pe ^ {t} + q)}$

.

Aussi les premiers cumulateurs

${displayStyle kappa _ {1} = np, kappa _ {2} = npq}$

Et l’équation de la récursivité s’applique

${displayStyle kappa _ {k + 1} = p (1-p) {frac {dkappa _ {k}} {dp}}.}$

Fonction caractéristique [ Modifier | Modifier le texte source ]]

La fonction caractéristique a la forme

${displayStyle phi _ {x} (s) = Left (Left (1-preght) + pmAtHrm {e} ^ {mathrm {i} s} droit) ^ {n} = Left (q + pmathrm {e} ^ {mathrm {i} s} droite) ^ {n}.}$

Fonction de génération de probabilité [ Modifier | Modifier le texte source ]]

Pour la fonction de génération de probabilité que vous obtenez

${displayStyle g_ {x} (s) = (ps + (1-p)) ^ {n}.}$

Fonction de génération de moment [ Modifier | Modifier le texte source ]]

La fonction générateurs de moment de la distribution binomiale est

$mm esclave tale tlek a mam simple routine – pppeo) mpie myo m hé hé hé éé kí huplome mmm tupe hmm tmm ra peut croire.$

Somme de tailles aléatoires distribuées binomiales [ Modifier | Modifier le texte source ]]

Pour la somme

${displaystyle z = x + y}$

Deux tailles aléatoires distribuées binomiales indépendantes

${displaystyle x}$

et

${displaystyle y}$

Avec les paramètres

${displaystyle n_ {1}}$

,

${displaystyle p}$

et

${displayStyle n_ {2}}$

,

${displaystyle p}$

Si vous obtenez les probabilités individuelles en utilisant l’identité de Vanderondeschen

${displayStyle {begin {aligned} opératorname {p} (z = k) & = sum _ {i = 0} ^ {k} Left [{binom {n_ {1}} {i}} p ^ {i} (1-p) ^ {n_ {1} -I} } ath + n_ {2}), end {aligné}}}$

Encore une fois une taille aléatoire distribuée binomiale, mais avec les paramètres

${displaystyle n_{1}+n_{2}}$

et

${displaystyle p}$

. S’applique donc au pliage

$m Discutez de ce Yleples espère Emry Hale Hys) ** M M Kueo Is Malm (Mary, Mép MM)) Mée Mupm)$

La distribution binomiale est donc reproductive pour

${displaystyle p}$

ou forme un groupe pliant.

Si la somme

${displaystyle z = x + y}$

est connu, chacune des variables aléatoires suit

${displaystyle x}$

et

${displaystyle y}$

Dans cette condition d’une distribution hypergéométrique. Pour ce faire, la probabilité conditionnelle est calculée:

${DisplayStyle {begin {aligned} p (x = ell | z = k) & = {fraude {p (x = ell cap z = k)} {p (z = k)}}} \ & = {fraude)} {p (z = k)}} \ & = {Fra {{binom {n_ {1} -p) ^ {n_ {1} -ell} {binom {n_ {2}} {k -ll} -k + ell}} {{binom {n_ {1} + n_ {2}} {k}} p ^ {k} (1-p) ^ {n_ {1} + n_ {2} -}}}}}}}}}}}}}}}}}}}}} {2}} Arian$

Cela représente une distribution hypergéométrique.

En général: si le

${displaystyle m}$

Variables aléatoires

${displayStyle x_ {i}}$

sont stochastiques indépendantes et les distributions binomiales

${displayStyle b (n_ {i}, p)}$

assez, alors la somme est aussi

${DisplayStyle x_ {1} + x_ {2} + dotsb + x_ {m}}$

Binomial distribué, mais avec les paramètres

${DisplayStyle n_ {1} + n_ {2} + dotsb + n_ {m}}$

et

${displaystyle p}$

. Ajoute des variables aléatoires distribuées binomiales

${displayStyle x_ {1}, x_ {2}}$

avec

${displayStyle p_ {1} neq p_ {2}}$

, alors vous obtenez une distribution binomiale généralisée.

Relation avec la distribution de Bernoulli [ Modifier | Modifier le texte source ]]

Un cas particulier de distribution binomiale pour

${displayStyle n = 1}$

est la distribution de Bernoulli. La somme des tailles aléatoires indépendantes et identiques à bernoulli est donc suffisante pour la distribution binomiale.

Relation avec la distribution binomiale généralisée [ Modifier | Modifier le texte source ]]

La distribution binomiale est un cas particulier de distribution binomiale généralisée avec

${displayStyle p_ {i} = p_ {j}}$

pour tous

${displayStyle I, Jin {1, DOTSC, n}}$

.
Il est plus précis pour la valeur des attentes fixes et l’ordre fixe de la distribution binomiale généralisée avec une entropie maximale. ^[dix]

Transition vers la distribution normale [ Modifier | Modifier le texte source ]]

Selon la phrase de Moivre-Laplace, la distribution binomiale converge dans l’affaire limite

${displaystyle nto infty}$

Contre une distribution normale, d. Autrement dit, la distribution normale peut être utilisée comme une approximation utile de la distribution binomiale si la taille de l’échantillon est suffisamment grande et que la proportion de la recherche n’est pas trop petite. Avec le conseil d’administration de Galton, vous pouvez comprendre expérimentalement l’approche de la distribution normale.

Ça s’applique

${displayStyle mu = np}$

et

${displayStyle Sigma ^ {2} = npq.}$

En insérant dans la fonction de distribution

${displaystyle phi}$

La distribution normale standard suit

${displayStyle b (kmid p, n) approx phi gauche ({k + 0 {,} 5-np sur {sqrt {npq}}} droit) – phi gauche ({k-0 {,} 5-np sur {sqrt {npq}} à droite) 1} {sqrt {2pi}}}, cdot exp Left (- {{(k-np)} ^ {2} sur 2npq} à droite).}$

Quant à voir, le résultat n’est rien de plus que la valeur fonctionnelle de la distribution normale pour

${displayStyle x = k}$

,

${displayStyle mu = ncdot p}$

ainsi que

${displayStyle Sigma ^ {2} = ncdot pcdot q}$

(lequel est également vivant comme la zone du

${displaystyle k}$

-Te rayures de l’histogramme du Standardisé Distribution binomiale avec

${DisplayStyle 1 / Sigma}$

Comme sa largeur et

${displaystyle phi ((k-mu) / sigma)}$

comme sa hauteur). ^[11] L’approche de la distribution binomiale à la distribution normale est utilisée dans la proximité normale des singes afin de déterminer rapidement la probabilité de nombreux niveaux de distribution binomiale, surtout s’il n’y a plus de valeurs de tableau (plus) pour eux.

Transition vers la distribution de Poisson [ Modifier | Modifier le texte source ]]

Une distribution binomiale asymétrique, dont la valeur des attentes

${DisplayStyle NP}$

pour

${displaystyle nrightarrow infty}$

et

${displaystyle PRIGHTARROW 0}$

Contre une constante

${displaystyle lambda}$

Converged, vous pouvez aborder la distribution de Poisson. La valeur

${displaystyle lambda}$

est alors la valeur des attentes pour toutes les distributions binomiales considérées dans la formation de valeur limite ainsi que pour la distribution de Poisson résultante. Ce rapprochement est également appelé approximation de Poisson, la valeur frontalière de Poisonsonsch ou la loi des événements rares.

${displayStyle {begin {aligned} b (kmid p, n) & = {n choisissez k} p ^ {k}, (1-p) ^ {n-k} = {frac {n!} {(n-k)!, k!}} Left ({frac {np} {n}} n}} à droite) ^ {n-k} \ & = {frac {n (n-1) (n-2) dotsm (n-k + 1)} {n ^ {k}}}, {frac {(np) ^ {k}} {k!}} Left (1- {frac {np} {n}} {frac {1} {n}} droite) gauche (1- {frac {2} {n}} droite) DOTSM gauche (1- {frac {k-1} {n}} droit) {frac {(np) ^ {k}} {k!}} Left (1- {{Frac {(np) {n}} } \ & to, {frac {lambda ^ {k}} {k!}} mathrm {e} ^ {- lambda}, quad {text {mit}} quad lambda = ncdot {} pquad {text {wenn}} quad nto infty {text {text} }$

Une règle de base dit que cette approximation est utilisable si

${displaystyle ngeq 50}$

et

${DisplayStyle Elder 0 {,} 05}$

.

La distribution de Poisson est donc la distribution aux frontières de la distribution binomiale pour les grands

${displaystyle n}$

et peu

${displaystyle p}$

, Il s’agit d’une convergence dans la distribution.

Relation avec la distribution géométrique [ Modifier | Modifier le texte source ]]

Le nombre d’échecs jusqu’à la première occurrence du succès est décrit par la distribution géométrique.

Relation avec la distribution binomiale négative [ Modifier | Modifier le texte source ]]

La distribution binomiale négative, en revanche, décrit la distribution de probabilité du nombre de tentatives nécessaires pour atteindre un nombre donné de succès dans un processus de Bernoulli.

Relation avec la distribution hypergéométrique [ Modifier | Modifier le texte source ]]

Dans le cas de la distribution binomiale, les échantillons sélectionnés sont retournés au volume de sélection, afin qu’ils puissent être sélectionnés à nouveau à une date ultérieure. En revanche, les échantillons ne sont pas retournés dans la population, la distribution hypergéométrique est utilisée. Les deux distributions vont dans une large mesure

${displaystyle n}$

la population et une petite étendue

${displaystyle n}$

Les échantillons ont fusionné. En règle générale, pour

${displayStyle n / nleq 0 {,} 05}$

Même si les échantillons ne sont pas suivis, la distribution binomiale peut être utilisée à la place de la distribution hypergéométrique mathématiquement plus exigeante, car les deux dans ce cas ne fournissent que des résultats légèrement différents.

Relation avec la distribution multinomiale [ Modifier | Modifier le texte source ]]

La distribution binomiale est un cas particulier de distribution multinomiale.

Relation avec la distribution Rademacher [ Modifier | Modifier le texte source ]]

Est

${displaystyle y}$

Binôme distribué au paramètre

${displayStyle p = 0 {,} 5}$

et

${displaystyle n}$

, ainsi peut

${displaystyle y}$

Comme une somme à l’échelle de

${displaystyle n}$

Variables aléatoires distribuées par Rademacher

${displayStyle x_ {1}, dotsc, x_ {n}}$

représenter:

${displayStyle y = 0 {,} 5Left (n + sum _ {i = 1} ^ {n} x_ {i} droit)}$

Cela est particulièrement évident dans la marche aléatoire symétrique

${displaystyle mathbb {z}}$

utilisé.

Relation avec la distribution de Panjer [ Modifier | Modifier le texte source ]]

La distribution binomiale est un cas particulier de la distribution de Panjer, qui combine la distribution de la distribution binomiale, de la distribution binomiale négative et de la distribution de Poisson dans une classe de distribution.

Relation avec la distribution bêta [ Modifier | Modifier le texte source ]]

Pour de nombreuses applications, il est nécessaire de distribuer la fonction de distribution

$mm esclave Slex Sever certains yem ãal dit que vous pensez que Mat Yourself Hyuk, hyuks$

à calculer spécifiquement (par exemple dans les tests statistiques ou pour les intervalles de confiance).

La relation suivante à la distribution bêta aide ici:

${displayStyle sum _ {i = 0} ^ {k} {binom {n} {i}} cdot p ^ {i} cdot (1-p) ^ {n-i} = operatorname {beta} (1-p; n-k; k + 1)}}$

C’est pour des paramètres positifs entier

${displaystyle a}$

et

${displaystyle b}$

:

${displayStyle OperatorName {beta} (x; a; b) = {(a + b-1)! Over (a-1)! cdot (b-1)!} int _ {0} ^ {x} u ^ {a-1} (1-u) ^ {b-1}, mathrm {d} u}$

À l’équation

${displayStyle sum _ {i = 0} ^ {k} {binom {n} {i}} cdot p ^ {i} cdot (1-p) ^ {n-i} = {n! sur (n-k-1)! CDOT K!} int _ {0} ^ {1-p} u ^ {n-k-1} (1-u) ^ {k}, mathrm {d} u}$

Pour prouver, on peut procéder comme suit:

• Le côté gauche et droit vote pour
  ${displayStyle p = 0}$

  correspondre (les deux côtés sont 1).

• Les dérivations après
  ${displaystyle p}$

  vote pour le côté gauche et droit de l’équation, car ils sont tous les deux les mêmes

  ${displayStyle – {n! Over (n-k-1)! CDOT K!} CDOT P ^ {K} CDOT (1-P) ^ {N-K-1}}$

  . Pour la dérivation du côté droit, voir la règle Leibniz pour l’intégrale des paramètres.

Relation avec la distribution binomiale bêta [ Modifier | Modifier le texte source ]]

Une distribution binomiale, son paramètre

${displaystyle p}$

Est distribué par bêta, est appelé une distribution binomiale bêta. C’est une distribution mixte.

Relation avec la distribution de pólya [ Modifier | Modifier le texte source ]]

La distribution binomiale est un cas particulier de la distribution Pólya (choisissez

${displayStyle c = 0}$

).

Distribution binomiale symétrique ( p = 1/2) [ Modifier | Modifier le texte source ]]

• 

  p = 0,5 et n = 4, 16, 64

• 
• 

  Mise à l’échelle avec écart-type

Ce cas se produit au

${displaystyle n}$

-Fachen Talent de monnaie avec une monnaie équitable (probabilité de têtes égale au nombre, c’est-à-dire seulement 1/2). La première figure montre la distribution binomiale pour

${displayStyle p = 0 {,} 5}$

Et pour différentes valeurs de

${displaystyle n}$

En tant que fonction de

${displaystyle k}$

. Ces distributions binomiales sont symétriques du miroir autour de la valeur

${displayStyle k = n / 2}$

:

${DisplayStyle b (kmid 1/2; n) = b (n-kmid 1/2; n)}$

Ceci est illustré dans la deuxième figure.
La largeur de la distribution devient proportionnelle à l’écart type

${displayStyle Sigma = {frac {sqrt {n}} {2}}}$

. La valeur de la fonction à

${displayStyle k = n / 2}$

, c’est-à-dire le maximum de la courbe, tombe proportionnellement

${DisplayStyle Sigma}$

.

En conséquence, on peut être des distributions binomiales avec différents

${displaystyle n}$

Échelle les uns sur les autres par l’abscisse

${displaystyle k-n / 2}$

à travers

${DisplayStyle Sigma}$

actions et l’ordonnée avec

${DisplayStyle Sigma}$

multiplié (troisième figure ci-dessus).

Le graphique adjacent montre les distributions binomiales redimensionnées, maintenant pour d’autres valeurs de

${displaystyle n}$

Et dans une miséricorde qui facilite la facilité de réalisation de toutes les valeurs fonctionnelles avec l’augmentation

${displaystyle n}$

converge contre une courbe commune. En utilisant la formule Stirling sur les coefficients binomiaux, vous pouvez voir que cette courbe (tirée en noir sur l’image) est une courbe de cloche Gaußsche:

${displayStyle f (x) = {frac {1} {sqrt {2pi}}}, {mathrm {e}} ^ {- {frac {x ^ {2}} {2}}}}$

.

C’est la densité de probabilité de la distribution normale standard

${displayStyle {Mathcal {n}} (0,1)}$

. Dans la limite centrale, cette constatation est si généralisée que les conséquences d’autres distributions de probabilité discrètes convergent contre la distribution normale.

Le deuxième graphique adjacent montre les mêmes données dans une application semi-logarithmique. Ceci est recommandé si vous souhaitez vérifier s’il existe des événements rares qui s’écartent de plusieurs écarts-types par rapport à la valeur des attentes, une distribution binomiale ou normale.

Tirer des balles [ Modifier | Modifier le texte source ]]

Il y a 80 balles dans un récipient, dont 16 jaunes. Une balle est retirée 5 fois puis couverte à nouveau. En raison du revêtement, la probabilité de tirer une boule jaune est également grande pour tous les retraits, à savoir 16/80 = 1/5. La valeur

${displayStyle Bleft (kmid {tfrac {1} {5}}; 5Right)}$

indique que précisément

${displaystyle k}$

Les balles retirées sont jaunes. Par exemple, nous nous attendons

${displayStyle k = 3}$

:

${displayStyle Bleft (3Mid {tfrac {1} {5}}; 5Right) = {binom {5} {3}} CDOT Left ({frac {1} {5}} droite) ^ {3} CDOT Left ({frac {4} {5}} droite) ^ {2} =} {1cdot 2}} CDOT {frac {1} {125}} cdot {frac {16} {25}} = {frac {64} {1250}} = 0 {,} 0512}$

Dans environ 5% des cas, exactement 3 boules jaunes sont tirées.

B (k | 0,2; 5)
k	Probabilité en%
0	00 32 768
d’abord	00 40.96
2	00 20.48
3	000 5.12
4	000 0,64
5	000 0,032
∑	0 100
Valeur adulte	000 d’abord
Variance	000 0.8

Nombre de personnes avec un anniversaire le week-end [ Modifier | Modifier le texte source ]]

La probabilité qu’une personne ait son anniversaire cette année est (par souci de simplicité) 2/7. 10 personnes restent dans une pièce. La valeur

${displayStyle b (kmid 2/7; 10)}$

donne (dans le modèle simplifié) la probabilité qui

${displaystyle k}$

Les personnes présentes cette année ont un anniversaire un week-end.

B (k | 2/7; 10)
k	Probabilité en% (arrondi)
0	000 3.46
d’abord	00 13.83
2	00 24.89
3	00 26.55
4	00 18.59
5	000 8.92
6	000 2.97
7	000 0,6797
8	000 0.1020
9	000 0,009063
dix	000 0.0003625
∑	0 100
Valeur adulte	000 2.86
Variance	000 2.04

Ensemble dans l’année ensemble [ Modifier | Modifier le texte source ]]

253 personnes se sont réunies. La valeur

${displayStyle b (kmid 1/365; 253)}$

indique que exactement

${displaystyle k}$

La personne présente un jour choisi au hasard a son anniversaire (sans considérer l’année).

B (k | 1/365; 253)
k	Probabilité en% (arrondi)
0	0 49,95
d’abord	0 34,72
2	0 12.02
3	00 2.76
4	00 0,47

La probabilité que “quelqu’un” de ces 253 personnes, c’est-à-dire H. Une ou plusieurs personnes qui ont un anniversaire ce jour-là est donc

${DisplayStyle 1-B (0mid 1/365; 253) = 50,05,$

.

Dans 252 personnes, la probabilité est

${displayStyle 1-b (0mid 1/365; 252) = 49,91,$

. Cela signifie que le seuil du nombre de personnes, à partir de laquelle la probabilité qu’au moins une de ces personnes ait un jour choisi au hasard de son anniversaire, soit supérieur à 50% est de 253 personnes (voir aussi le paradoxe de l’anniversaire).

Le calcul direct de la distribution binomiale peut être difficile en raison des grandes facultés. Une approximation de la distribution de Poisson est autorisée ici (

${displayStyle n> 50, p <0 {,} 05}$

). Avec le paramètre

${displaystyle lambda = np = 253/65}$

Les valeurs suivantes surviennent: ^[douzième]

P 253/365 (k)
k	Probabilité en% (arrondi)
0	0 50
d’abord	0 34.66
2	0 12.01
3	00 2.78
4	00 0,48

Intervalle de confiance pour une probabilité [ Modifier | Modifier le texte source ]]

Dans une enquête d’opinion

${displaystyle n}$

Personnes

${displaystyle k}$

Les gens à choisir la fête A. Déterminez un intervalle de confiance à 95% pour la proportion inconnue d’électeurs qui choisissent le parti A dans l’électorat global.

Une solution au problème sans L’enregistrement à la distribution normale peut être trouvé dans l’intervalle de confiance de l’article pour la probabilité de succès de la distribution binomiale.

Modèle d’utilisation [ Modifier | Modifier le texte source ]]

En utilisant la formule suivante, la probabilité peut être calculée que

${displaystyle k}$

depuis

${displaystyle n}$

Les gens une activité en moyenne

${displaystyle m}$

Minutes par heure Prises, exécutez en même temps.

${displayStyle p (x = k) = {n Choisissez K} cdot gauche ({frac {m} {60}} droit) ^ {k} cdot gauche (1- {frac {m} {60}} droit) ^ {n-k}}$

Erreurs statistiques de la fréquence des classes dans les histogrammes [ Modifier | Modifier le texte source ]]

L’affichage de la mesure indépendante entraîne un histogramme conduit au regroupement des valeurs mesurées dans les classes.

La probabilité de

${displaystyle n_ {i}}$

Entrées en classe

${displayStyle i}$

est donné par la distribution binomiale

${displayStyle b_ {n, p_ {i}} (n_ {i})}$

avec

${DisplayStyle n = sum n_ {i}}$

et

${DisplayStyle p_ {i} = {frac {n_ {i}} {n}}}$

.

Valeur d’attente et variance du

${displaystyle n_ {i}}$

Sont alors

${displayStyle e (n_ {i}) = np_ {i} = n_ {i}}$

et

${displayStyle v (n_ {i}) = np_ {i} (1-p_ {i}) = n_ {i} Left (1- {frac {n_ {i}} {n}} droit)}$

.

Cela réside l’erreur statistique du nombre d’entrées en classe

${displayStyle i}$

à

${displayStyle Sigma (n_ {i}) = {sqrt {n_ {i} Left (1- {frac {n_ {i}} {n}} droit)}}}$

.

Avec un grand nombre de classes,

${displayStyle p_ {i}}$

petit et petit

${displayStyle Sigma (n_ {i}) approx {sqrt {n_ {i}}}}$

.

Par exemple, la précision statistique des simulations de Monte Carlo peut être déterminée.

Les nombres aléatoires pour la distribution binomiale sont généralement générés en utilisant la méthode d’inversion.

Alternativement, vous pouvez également utiliser que la somme des variables aléatoires distribuées de Bernoulli est binomiale. Vous créez ceci

${displaystyle n}$

Bernoulli a distribué des nombres aléatoires et les ajoute; Le résultat est un nombre aléatoire distribué binomial.

Appeler la fonction de probabilité de la distribution binomiale dans les ordinateurs de poche et les logiciels mathématiques se produit généralement certains de certains , pdfbin ou Binomialpdf ( Fonction de densité de probabilité binomiale ). La fonction de distribution accumulée est avec cdfbin ou Binomialcdf ( Fonction de distribution cumulative binomiale ) abrégé. ^[13]

1. ↑ Peter Kissel: MAC08 Stochastics (partie 2). Darmstadt Study Community 2014, p. 12.
2. ↑ Bigalke, Köhler: Mathématiques 13.2 Cours de base et avancé. Cornelsen, Berlin 2000, p. 130.
3. ↑ George Udny Yule: Une introduction à la théorie des statistiques. Griffin, Londres 1911, S. 287.
4. ↑ Peter Kissel: MAC08 Stochastics. Partie 2e groupe d’étude Darmstadt 2014, p. 23.
5. ↑ Bigalke, / Köhler: Mathématiques 13.2 Cours de base et avancé. Cornelsen, Berlin 2000, p. 144 ff.
6. ↑ P. Neumann: Sur la médiane de la distribution binomiale et de Poisson . Dans: Magazine scientifique de l’Université technique de Dresde . 19e année, 1966, S. 29–33 .
7. ↑ Seigneur, Nick. (Juillet 2010). “Moyenne binomiale Lorsque la moyenne est un entier”, The Mathematical Gazette 94, 331–332.
8. ↑ ^{un b} R. Kaas, J.M. Buhrman: Moyenne, médiane et mode dans les distributions binomiales . Dans: Statistiques neerlandiques . 34e année, Non. d’abord , 1980, S. 13–18 , est ce que je: 10.1111 / j.1467-9574.1980.tb00681.x .
9. ↑ ^{un b} K. Hamza: La plus petite limite supérieure uniforme sur la distance entre la moyenne et la médiane des distributions binomiales et de Poisson . Dans: Statistiques et lettres de probabilité . 23e année, 1995, S. 21-25 , est ce que je: 10.1016 / 0167-7152 (94) 00090-in .
10. ↑ Peter Harremoës: Distributions binomiales et de Poisson comme distributions d’entropie maximales . Dans: Transactions IEEE sur la théorie de l’information . 47e année. IEEE Information Theory Society, 2001, S. 2039-2041 , est ce que je: 101109/18 930936 .
11. ↑ M. Brokate, N. Henze, F. Hettlich, A. Meister, G. Schranz-Kirchener, Th. Sonar: Connaissance de base des mathématiques: analyse plus élevée, numérique et stochastes. Springer-Verlag, 2015, p. 890.
12. ↑ Dans le cas spécifique, vous devez pour la distribution binomiale
    ${displayStyle gauche ({tfrac {364} {365}} droit) ^ {253}}$

    calculer et pour la distribution de Poisson

    ${displaystyle e ^ {- 253/365}}$

    . Les deux sont faciles avec la calculatrice. Dans le cas d’une facture avec du papier et du crayon, la série exponentielle 8 ou 9 est requise pour la valeur de la distribution de Poisson, tandis que pour la distribution binomiale au moyen de plusieurs carrés, vous arrivez à 256. puissance puis partagez à travers la troisième puissance.

13. ↑ Aide en ligne SCILAB – Statistiques. Consulté le 13 janvier 2022 .