Cet article décrit une fonction spéciale. Pour la formule qui décrit la transmission du rayonnement électromagnétique, voir la formule aérienne.
Le Fonction aérée
 Décrit une fonction spéciale en mathématiques. La fonction
Décrit une fonction spéciale en mathématiques. La fonction
 et la fonction connexe
et la fonction connexe
 , qui est également appelé fonction aérée, sont des solutions à l’équation différentielle linéaire
, qui est également appelé fonction aérée, sont des solutions à l’équation différentielle linéaire
-

Également connu comme une équation aérée. Entre autres choses, il décrit la solution à l’équation de Schrödinger pour un pot potentiel linéaire.
La fonction aérée porte le nom de l’astronome britannique George Biddell Airy, qui a utilisé cette fonction dans son travail dans l’optique (Airy 1838). La désignation
 a été présenté par Harold Jeffreys.
a été présenté par Harold Jeffreys.
Fonctionnalité vraie aérée [ Modifier | Modifier le texte source ]]
Pour les valeurs réelles
 La fonction aérée est définie comme une intégrale de paramètre:
La fonction aérée est définie comme une intégrale de paramètre:
-

Une deuxième solution indépendante linéaire à l’équation différentielle est le Fonction aérée du deuxième type
 :
:
-

Fonction aérée complexe [ Modifier | Modifier le texte source ]]
La fonction aérée complexe est
-

MIT KONTOUR
 depuis
depuis
 avec
avec
 après
après
 avec
avec
 .
.
Comportement asymptotique [ Modifier | Modifier le texte source ]]
Pour
 contre
contre
 peut être
peut être
 et
et
 Approximation à l’aide de l’approche WKB:
Approximation à l’aide de l’approche WKB:
-

Pour
 contre
contre
 Les relations s’appliquent:
Les relations s’appliquent:
-

zéro point [ Modifier | Modifier le texte source ]]
Les fonctions aériennes n’ont aucun point zéro sur l’axe réel négatif. [d’abord] L’emplacement approximatif découle du comportement asymptotique pour
 pour
pour
-

-

Valeurs spéciales [ Modifier | Modifier le texte source ]]
Les fonctions aérées et leurs dérivations ont pour
 Les valeurs suivantes:
Les valeurs suivantes:
-
![{displaystyle {begin{aligned}mathrm {Ai} (0)&{}={frac {1}{{sqrt[{3}]{9}}cdot Gamma ({frac {2}{3}})}},&quad mathrm {Ai} '(0)&{}=-{frac {1}{{sqrt[{3}]{3}}cdot Gamma ({frac {1}{3}})}},\mathrm {Bi} (0)&{}={frac {1}{{sqrt[{6}]{3}}cdot Gamma ({frac {2}{3}})}},&quad mathrm {Bi} '(0)&{}={frac {sqrt[{6}]{3}}{Gamma ({frac {1}{3}})}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a85175b026a300ea1e494ba99b326df0e329f29f)
Mentionné ici
 La fonction gamma. Il s’ensuit que le déterminant de Wronski de
La fonction gamma. Il s’ensuit que le déterminant de Wronski de
 et
et
 même
même
 est.
est.
Directement à partir de la définition de la fonction aérée
 (voir ci-dessus) suit leur Fourier transformé.
(voir ci-dessus) suit leur Fourier transformé.
-

Notez la variante symétrique de la transformation de Fourier utilisée ici.
-

-

-
![{displaystyle mathrm {Ai} (x)={frac {1}{3}}{sqrt {x}}left[I_{-1/3}left({frac {2}{3}}x^{3/2}right)-I_{1/3}left({frac {2}{3}}x^{3/2}right)right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b1f0cd33e711461cb3ab410a2d4b0af8dcb99aca)
-
![{displaystyle mathrm {Bi} (x)={sqrt {frac {x}{3}}}left[I_{-1/3}left({frac {2}{3}}x^{3/2}right)+I_{1/3}left({frac {2}{3}}x^{3/2}right)right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9175279c9f086c7d1242484b4430f327531ed036)
- Une autre représentation intégrale infinie pour
 est le cas
est le cas
-

- Il y a les rangées de lignes [2]
-

-

 et
et
 sont des fonctions complètes. Ils peuvent donc être poursuivis analytiquement sur l’ensemble du niveau complexe.
sont des fonctions complètes. Ils peuvent donc être poursuivis analytiquement sur l’ensemble du niveau complexe.
Définir
-

par lequel
 La fonction hypergéométrique est.
La fonction hypergéométrique est.
Ensuite, il y a les généralisations suivantes de l’intégrale aérée
-

-

-

Fonction Airy-Zeta [ Modifier | Modifier le texte source ]]
En plus de la fonction aérée, la fonction Zeta Airysian peut être définie comme un analogue aux autres fonctions Zeta [3]
-

La somme des points zéro réels (négatifs) de
 va.
va.
Fonctions SCORESCHE [ Modifier | Modifier le texte source ]]
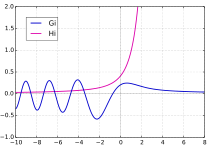
Graphiques fonctionnels de

et

.
Parfois, les deux autres fonctions sont également
 et
et
 ajouté aux fonctions aérées. Les définitions intégrales sont [4]
ajouté aux fonctions aérées. Les définitions intégrales sont [4]
-

-

Ils peuvent également être effectués par les fonctions
 et
et
 représenter.
représenter.
- ↑ Eric W. Pointerstein: Zéros de fonction aérée . Dans: Mathworld (Anglais).
- ↑ C. Banderier, P. Flajolet, G. Schaeffer, M. Soria: Cartes planes et phénomènes aérés. Dans Automates, langages et programmation. Actes du 27e colloque international (Icalp 2000) tenu à l’Université de Genève , Genève, 9.–15. Juli 2000 (éd. U. Montanari, J. D. P. Rolim, E. Welzl). Berlin: Springer, S. 388–402, 2000
- ↑ Eric W. Pointerstein: Fonction de zeta aérée . Dans: Mathworld (Anglais).
- ↑ Milton Abramowitz et Irene A. Stegun: Manuel des fonctions mathématiques avec des formules, des graphiques et des tables mathématiques , 1954, Page 447


 Décrit une fonction spéciale en mathématiques. La fonction
Décrit une fonction spéciale en mathématiques. La fonction  , qui est également appelé fonction aérée, sont des solutions à l’équation différentielle linéaire
, qui est également appelé fonction aérée, sont des solutions à l’équation différentielle linéaire 
 La fonction aérée est définie comme une intégrale de paramètre:
La fonction aérée est définie comme une intégrale de paramètre: 
 :
: 

 depuis
depuis  avec
avec  après
après  avec
avec  .
.  peut être
peut être  et
et  Approximation à l’aide de l’approche WKB:
Approximation à l’aide de l’approche WKB: 
 Les relations s’appliquent:
Les relations s’appliquent: 
 pour
pour 

 Les valeurs suivantes:
Les valeurs suivantes: ![{displaystyle {begin{aligned}mathrm {Ai} (0)&{}={frac {1}{{sqrt[{3}]{9}}cdot Gamma ({frac {2}{3}})}},&quad mathrm {Ai} '(0)&{}=-{frac {1}{{sqrt[{3}]{3}}cdot Gamma ({frac {1}{3}})}},\mathrm {Bi} (0)&{}={frac {1}{{sqrt[{6}]{3}}cdot Gamma ({frac {2}{3}})}},&quad mathrm {Bi} '(0)&{}={frac {sqrt[{6}]{3}}{Gamma ({frac {1}{3}})}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a85175b026a300ea1e494ba99b326df0e329f29f)
 La fonction gamma. Il s’ensuit que le déterminant de Wronski de
La fonction gamma. Il s’ensuit que le déterminant de Wronski de  est.
est. 


![{displaystyle mathrm {Ai} (x)={frac {1}{3}}{sqrt {x}}left[I_{-1/3}left({frac {2}{3}}x^{3/2}right)-I_{1/3}left({frac {2}{3}}x^{3/2}right)right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b1f0cd33e711461cb3ab410a2d4b0af8dcb99aca)
![{displaystyle mathrm {Bi} (x)={sqrt {frac {x}{3}}}left[I_{-1/3}left({frac {2}{3}}x^{3/2}right)+I_{1/3}left({frac {2}{3}}x^{3/2}right)right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9175279c9f086c7d1242484b4430f327531ed036)





 La fonction hypergéométrique est.
La fonction hypergéométrique est.







Recent Comments