Bayesche Netz – Wikipedia

Posted on November 26, 2023 by lordneo

before-content-x4

UN Réseau de Bayesch ou Réseau de Bayes (Nommé d’après Thomas Bayes) est un graphique azyclique dirigé (DAG), dans lequel les nœuds décrivent des variables aléatoires et les bords dus aux variables. Chaque nœud du réseau se voit attribuer une distribution de probabilité conditionnelle de la variable aléatoire représentée par elle, compte tenu des variables aléatoires sur les nœuds parents. Ils sont décrits par des tableaux de probabilité. Cette distribution peut être arbitraire, mais elle est souvent utilisée pour travailler avec des distributions discrètes ou normales. Les parents d’un nœud V sont les nœuds qui mènent à V.

after-content-x4

Un réseau bavarois sert à représenter la distribution de probabilité commune de toutes les variables impliquées dans l’utilisation de l’indépendance conditionnelle connue aussi compacte que possible. La dépendance conditionnelle (UN) sur le sous-ensemble des variables est combinée avec les connaissances A-priori.

Sont X _d’abord, …, X _nCertaines des variables aléatoires (qui sont terminées en ajoutant des variables parentales), leur distribution commune est calculée comme

{displayStyle p (x_ {1}, points, x_ {n}) = prod _ {i = 1} ^ {n} p (x_ {i} | mathrm {elterne} (x_ {i}));.

Y a-t-il

{displayStyle p (x_ {1}, points, x_ {n})}

${displaystyle P(X_{1},dots ,X_{n})}$ Une orthographe symbolique pour la distribution de probabilité commune des variables aléatoires

{displayStyle x_ {1}, points, x_ {n}}

$X_{1},dots ,X_{n}$ .
Si un nœud n’a pas de parents, la distribution associée de la probabilité est une distribution inconditionnelle.

Comme dans l’exemple ci-dessous, on vous intéresse souvent à une probabilité marginale qui peut être effectuée par marginalisation sur toutes les réalisations possibles

after-content-x4

{displayStyle x_ {j}}

$x_{j}$ Dans la salle d’État

{displayStyle e_ {j}}

$E_{j}$ La variable aléatoire

{displayStyle x_ {j}}

$X_{j}$ reçoit:

{displayStyle p (x_ {1} = x_ {1}) = sum _ {x_ {2} dans e_ {2}} Dots sum _ {x_ {n} dans e_ {n}} p (x_ {1} = x_ {1}, les points, x_ {n} = x_ {n}).

Exemple d’un réseau bavarois avec trois nœuds et deux bords. Les valeurs de la fonction de probabilité sont en haut à gauche des tables

{displayStyle p (w)}

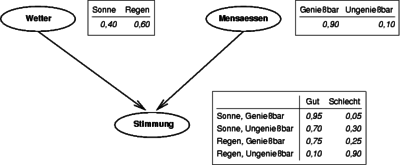
Dans l’exemple, les trois variables aléatoires se forment

{displayStyle in}

$W$ = Temps,

{displaystyle m}

$M$ = Cafétéria et

{DisplayStyle S}

$S$ = Humeur les nœuds d’un réseau bavarois. En plus des nœuds pour les variables aléatoires

{displayStyle in}

$W$ et

{displaystyle m}

$M$ reçoivent leurs distributions de probabilité inconditionnelles. En plus du nœud pour la variable aléatoire

{DisplayStyle S}

$S$ Sont quatre distributions de probabilité conditionnelles pour une variable aléatoire

{DisplayStyle S}

$S$ , compte tenu des quatre combinaisons possibles de

{displayStyle in}

$W$ et

{displaystyle m}

$M$ , indiqué.
Les deux variables aléatoires

{displayStyle in}

$W$ et

{displaystyle m}

$M$ Sont les parents de

{DisplayStyle S}

$S$ Et n’ont pas de parents. Les deux flèches (bords) sont interprétées de manière causale.

La distribution commune de la probabilité est calculée en raison de l’indépendance stochastique de M et W comme suit:

{displayStyle operatorname {p} (s, w, m) = operatorname {p} (smid w, m) cdot operatorname {p} (w) cdot opératorname {p} (m)}

Par conséquent, avec l’aide de la loi de la probabilité totale, suit la distribution marginale

m tume flay felement fey em. 2) mmumm mook tom embé Quupe mupe mót m kmuk, comme sur euan, ”

Avec les distributions de probabilité spécifiées, la distribution de bord de

{DisplayStyle S}

$S$ déterminer. Par exemple, s’applique

{displaystyle {begin{alignedat}{1}operatorname {P} (S={text{gut}})&= &operatorname {P} (S={text{gut}}mid W={text{Sonne}},M={text{genießbar}})cdot operatorname {P} (W={text{Sonne}})cdot operatorname {P} (M={text{genießbar}})\&&+ operatorname {P} (S={text{gut}}mid W={text{Sonne}},M={text{ungenießbar}})cdot operatorname {P} (W={text{Sonne}})cdot operatorname {P} (M={text{ungenießbar}})\&&+ operatorname {P} (S={text{gut}}mid W={text{Regen}},M={text{genießbar}})cdot operatorname {P} (W={text{Regen}})cdot operatorname {P} (M={text{genießbar}})\&&+ operatorname {P} (S={text{gut}}mid W={text{Regen}},M={text{ungenießbar}})cdot operatorname {P} (W={text{Regen}})cdot operatorname {P} (M={text{ungenießbar}})\&= &0{,}95cdot 0{,}40cdot 0{,}90+0{,}70cdot 0{,}40cdot 0{,}10+0{,}75cdot 0{,}60cdot 0{,}90+0{,}10cdot 0{,}60cdot 0{,}10;,end{alignedat}}}

Toutes les probabilités requises peuvent être trouvées dans les trois tables.

Peut aussi être terminé

{displayStyle operatorname {p} (s = s, w = w, m = m) = opératorname {p} (s = smid w = w, m = m) opératorname {p} (w = w, m = m) = opératorname {p} (s = smid w = w, m) p (w = w) p (m = m)}

pour

{DisplayStyle sin {{text {good}}, {text {bad}}}}

${displaystyle sin {{text{gut}},{text{schlecht}}}}$ ,

{DisplayStyle win {text {Sun}}, {text {rain}}}}

${displaystyle win {{text{Sonne}},{text{Regen}}}}$ et

{DisplayStyle min {{text {agréable}}, {text {nonectible}}}}

${displaystyle min {{text{genießbar}},{text{ungenießbar}}}}$ La distribution commune de la probabilité de

{DisplayStyle S}

$S$ ,

{displayStyle in}

$W$ et

{displaystyle m}

$M$ déterminer. Le premier signe d’égalité résulte de la définition d’une probabilité conditionnelle et le deuxième signe d’égalité utilise l’indépendance stochastique des variables aléatoires

{displayStyle in}

$W$ et

{displaystyle m}

$M$ . Z. B. doré

{DisplayStyle {begin {aligned} opératorname {p} (s = {text {good}}, w = {text {Sun}}, m = {text {génie}) & = operatorname {p} (s = m = {text {agréable}) \ & = 0 {,} 95cdot 0 {,} 40cdot 0 {,} 90end {aligné}}

De même, sept autres probabilités pour toutes les autres combinaisons de valeurs de variables aléatoires peuvent être

{DisplayStyle S}

$S$ ,

{displayStyle in}

$W$ et

{displaystyle m}

$M$ calculer.

La distribution commune de la probabilité de

{DisplayStyle S}

$S$ et

{displayStyle in}

$W$ vous obtenez de la distribution de probabilité commune de

{DisplayStyle S}

$S$ ,

{displayStyle in}

$W$ et

{displaystyle m}

$M$ quand

{DisplayStyle operatorname {p} (s = s, w = w) = opératorname {p} (s = s, w, m = {text {gremable}) + opératorname {p} (s = s, w, m = {text {nonedible}})}}

pour

{DisplayStyle sin {{text {good}}, {text {bad}}}}

${displaystyle sin {{text{gut}},{text{schlecht}}}}$ et

{DisplayStyle win {text {Sun}}, {text {rain}}}}

${displaystyle win {{text{Sonne}},{text{Regen}}}}$ .

S’il est connu que l’humeur est bonne, la probabilité de temps ensoleillé peut être attiré:

{Displaystyle {Begin {aligned} operatorname {p} (w = {text {sun}} mid s = {text {gut}) & = {frac {operatorname {p} (s = {text {gut}}, w = {text {sun}}} {p} (s = {text {text }}}} \ & = {frac {operatorname {p} (s = {text {good}}, w = {text {sun})} {operatorname {p} (s = {text {good}}, w = {text {sun}})+operatorname {p} (text}, w =}} {Rain})};, end {aligned}}}

où toutes les probabilités requises de la distribution de probabilité commune de

{DisplayStyle S}

$S$ et

{displayStyle in}

$W$ résultat.

Provient de certaines des variables, à propos ET _d’abord, …, ET _m, la valeur connue, d. H. Si des preuves sont disponibles, à l’aide de divers algorithmes, la distribution de probabilité conditionnelle de X _d’abord, …, X _nAvec donné ET _d’abord, …, ET _msont calculés et donc opérés.

Le problème d’inférence, à la fois exactement et approximatif, dans les réseaux de Bayes, est NP-Shw. Des procédures approximatives sont disponibles dans des réseaux plus grands. Les procédures exactes sont un peu plus précises qu’approximativement, mais cela ne joue souvent qu’un rôle insignifiant dans la pratique, car les réseaux bayésiens sont utilisés pour prendre des décisions où les probabilités exactes ne sont pas nécessaires.

Il convient de noter que, dans le cas des implémentations logicielles, précisément seulement deux fois des numéros de virgules coulissants précis sont utilisés. Cela limite la précision de ces calculs.

Table of Contents

Inférence exacte [ Modifier | Modifier le texte source ]]

Pour l’inférence exacte à Bayesche Netzen, entre autres. ce qui suit
Algorithmes:

Approximative Inferenz [ Modifier | Modifier le texte source ]]

Types d’inférence [ Modifier | Modifier le texte source ]]

Diagnostic: des effets aux causes
Causal: des causes aux effets
Intercausal: entre les causes d’un effet commun
Mixte: combinaison de la précédente

Si un réseau bavarois doit être généré automatiquement à partir des données disponibles, qui décrit les données ainsi que possible, deux problèmes possibles surviennent: soit la structure du graphique du réseau est déjà donnée et vous n’avez plus à prendre soin de la détermination de l’indépendance conditionnelle, mais uniquement pour calculer la distribution conditionnelle sur le nœud du réseau, ou vous devez également apprendre une structure d’un réseau adapté en plus des paramètres.

Paramètre d’apprentissage [ Modifier | Modifier le texte source ]]

Si vous n’assumez pas un modèle de probabilité complet (bayésien), vous choisissez généralement

comme méthode d’estimation. En cas de modèle de probabilité complet (Bayesche), l’estimation du point est

à. Les maxima locaux de la probabilité ou du Postériorifusten en cas de données complètes et de variables entièrement observées peuvent généralement être utilisées avec des algorithmes d’optimisation communs tels que

être trouvé. Pour que le cas des observations manquantes soit considérée comme la règle), la puissante et la répartition sont généralement

utilisé.

Apprentissage structurel [ Modifier | Modifier le texte source ]]

L’apprentissage structurel peut avec l’algorithme K2 (approximativement, en utilisant une fonction cible appropriée) ou l’algorithme PC.

Pour déterminer l’indépendance conditionnelle de deux quantités de variables, un tiers de ces quantités est suffisant pour examiner la structure du graphique du réseau. On peut montrer que le concept (théorique graphique) de la séparation D coïncide avec le concept d’indépendance conditionnelle.

Les moustiquaires Bayesch sont utilisés comme une forme de systèmes d’experts probabilistes, par lesquels les domaines d’application se trouvent en bioinformatique, analyse des échantillons, médecine et sciences de l’ingénierie. Dans la tradition de l’intelligence artificielle, l’accent est mis sur Bayescher Netze sur l’utilisation de leurs structures graphiques pour permettre des conclusions abducteurs et déductives qui seraient inspectives dans une probabilité non liée. Ceci est réalisé par les différents algorithmes d’inférence.

L’idée de base des réseaux de Bayescher, à savoir la factorisation graphique d’un modèle de probabilité, est également utilisée dans d’autres traditions, telles que dans les statistiques bayésiennes et dans la tradition des modèles graphiques So appelés à des fins de modélisation des données. Les domaines d’application sont principalement l’épidémiologie, la médecine et les sciences sociales.

Enrique Castillo, Jose Manuel Gutierrez, Ali S. Hadi: Systèmes experts et modèles de réseau probabiliste . Springs-Publinging, New York 1997, ISBN 0-387-94858-9.
Finn V. Jensen: Réseaux bayésiens et graphiques de décision . Spring Pleans, New York, New Hork 2001, ISBN 0-387-9525259-4.
Richard E. Napolitan: Apprendre les réseaux bayésiens . Prentice Hall, 2003, ISBN 0-13-012534-2.
Judea Pearl: Raisonnement probabiliste dans les systèmes intelligents: réseaux d’inférence plausible . Morgan Kauffmann Publishers, San Francisco 1988, ISBN 0-934613-73-7
Judea Pearl: Causalité . Cambridge University Press, Cambridge 2000, ISBN 0-521-77362-8.
Stuart Russell, Peter Norvig: Intelligence artificielle – une approche moderne . Pearson Education Allemagne, Allemagne 2004, ISBN 3-8273-7089-2.

after-content-x4

Bayesche Netz – Wikipedia

Inférence exacte [ Modifier | Modifier le texte source ]]

Approximative Inferenz [ Modifier | Modifier le texte source ]]

Types d’inférence [ Modifier | Modifier le texte source ]]

Paramètre d’apprentissage [ Modifier | Modifier le texte source ]]

Apprentissage structurel [ Modifier | Modifier le texte source ]]

Recent Posts

Recent Comments

Archives

Categories

Meta