Nullfunktion – wikipedia

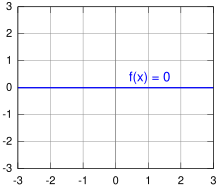
Le Fonction nul est une fonction en mathématiques, en particulier l’analyse, le nombre de la valeur est toujours nul quelle que soit la valeur. Plus général est que Zéro ou la Nulloperateur Dans l’algèbre linéaire, une illustration entre deux salles vectorielles, ce qui entraîne toujours le vecteur zéro de la zone cible. L’illustration zéro dans l’algèbre est capturée encore plus généralement et il y a une illustration de toute quantité en quantité dans laquelle un lien avec un élément neutre est défini, ce qui entraîne toujours cet élément neutre. La fonction zéro a de nombreuses propriétés et est souvent utilisée en mathématiques comme exemple ou comme contre-exemple. Il s’agit de la solution triviale d’un certain nombre de problèmes mathématiques, tels que des équations différentielles linéaires homogènes et des équations intégrales.

Définition [ Modifier | Modifier le texte source ]]

En analyse réelle, une fonction zéro est la fonction réelle

${affichestyle phi colon mathbb {r} à mathbb {r}}$

qui attribue le numéro zéro à chaque argument, c’est-à-dire qu’il s’applique

${DisplayStyle phi (x) = 0}$

pour tous

${displaystyle xin mathbb {r}}$

. À l’aide du symbole d’identité, la fonction zéro est également à travers

${displaystyle phi equiv 0}$

écrit. Le graphique de la fonction zéro est l’axe x entier. Parfois, la plage de définition de la fonction zéro est également sur un sous-ensemble

${DisplayStyle Omega Sous-ensemble Mathbb {R}}$

limité.

Caractéristiques [ Modifier | Modifier le texte source ]]

classification [ Modifier | Modifier le texte source ]]

La fonction zéro est un cas particulier des classes fonctionnelles suivantes:

Symétrie [ Modifier | Modifier le texte source ]]

La fonction zéro est la seule fonction en même temps et impair, c’est-à-dire qu’elle s’applique

${DisplayStyle phi (x) = phi (-x) = -phi (x)}$

.

De plus, il n’est ni positif ni négatif, mais il est à la fois non positif et non négatif, c’est-à-dire

${Displaystyle phi (x) leq 0}$

et

${displaystyle phi (x) geq 0}$

.

Les positions zéro de la fonction zéro sont tous des nombres de la quantité de définition et leur quantité de points non zéro est donc vide. La fonction nul minimum et maximale est également nulle:

${DisplayStyle max _ {s’il vous plaît mathbb {r}}} non – (x) = min _ {s’il vous plaît mathbb {r}}} (x) = 0}$

.

De plus, la fonction zéro, comme toute fonction constante, augmente et tombe (mais pas stricte) et, comme toute fonction linéaire, en même temps convexe et concave.

Dérivation [ Modifier | Modifier le texte source ]]

La fonction zéro est une fonction fluide, c’est-à-dire aussi souvent que possible, régulièrement différenciée, par laquelle chacune de ses dérivations est à nouveau la fonction zéro elle-même, c’est-à-dire

${DisplayStyle phi ^ {(n)} (x) = phi (x)}$

pour chaque

${Displaystyle nin mathbb {n}}$

. En plus de la fonction exponentielle, la fonction zéro est la seule fonction avec cette propriété. La fonction zéro elle-même est la dérivation d’une fonction constante et en général le

${displayStyle (n + 1)}$

-Te dérivation d’un polynôme à partir du degré

${displaystyle n}$

.

Intégral [ Modifier | Modifier le texte source ]]

L’intégrale de la fonction zéro entraîne toujours zéro quelles que soient les limites d’intégration, c’est-à-dire

${DisplayStyle int _ {a} ^ {b} phi (x) ~ dx = 0}$

.

pour tous

${displaystyle a, bin mathbb {r} cup {-infty, infty}}$

. La fonction zéro est la seule fonction polynomiale qui peut être intégrée sur toute la figure réelle. La fonction STEM de la fonction zéro est la fonction zéro elle-même et, puisque la constante d’intégration est librement sélectionnable, chaque fonction constante.

Solution d’équations [ Modifier | Modifier le texte source ]]

La fonction zéro est la solution triviale des quatre équations fonctionnelles de Cauchy: ^[d’abord]

${displayStyle {begin {aligned} f (x + y) & = f (x) + f (y) \ f (x + y) & = f (x) cdot f (y) \ f (xcdot y) & = f (x) + f (y) \ f (xcdot y) & = f (x) cdot f (y) \ end {alligned}}}$

De plus, la fonction zéro résout toute équation différentielle linéaire homogène de la forme

${DisplayStyle a_ {n} (x) f ^ {(n)} (x) + a_ {n-1} (x) f ^ {(n-1)} + dotsb + a_ {1} (x) f ‘(x) + a_ {0} (x) f (x) f () = 0}$

et chaque équation intégrale linéaire homogène de l’espèce

${displaystyle lambda f (x) + int _ {a} ^ {x} k (x, y) f (y) ~ dy = 0}$

avec intégral

${displayStyle k (x, y)}$

et facteur préliminaire

${displaystyle lambda}$

. Inversement, l’équation différentielle linéaire ou intégrale inhomogène n’est jamais résolue par la fonction zéro.

Définition [ Modifier | Modifier le texte source ]]

Dans l’algèbre linéaire, une illustration est appelée

${Displaystyle phi colon vto w}$

Entre deux vecteurs

${DisplayStyle V}$

et

${displayStyle in}$

Au-dessus du même corps

${displaystyle k}$

Image zéro ou opérateur zéro si pour tous les vecteurs

${Displaystyle vin v}$

${DisplayStyle phi (v) = 0_ {w}}$

s’applique, bien que

${Déplastyle 0_ {w}}$

Le vecteur zéro clairement déterminé de

${displayStyle in}$

est. Parfois, l’image zéro est également directement à travers

${DisplayStyle 0}$

S’il est clair à partir du contexte, a noté si l’image zéro ou le nombre est signifiée zéro. Ici aussi

${displayStyle usubset v}$

être restreint.

Exemples [ Modifier | Modifier le texte source ]]

Caractéristiques [ Modifier | Modifier le texte source ]]

Linéarité [ Modifier | Modifier le texte source ]]

L’illustration zéro est une illustration linéaire, c’est-à-dire l’homomorphisme d’un vecteurs, c’est-à-dire qu’elle s’applique

${DisplayStyle phi (av + bw) = aphi (v) + bphi (w)}$

pour tous

${DisplayStyle V, Win V}$

et

${DisplayStyle A, bin k}$

. Il se trouve donc dans la salle vectorielle des images linéaires

${displayStyle l (v, w)}$

Et il y a le vecteur zéro là-bas.

Toute image nulle entre les salles vectorielles finalement dimensionnelles est utilisée en ce qui concerne toutes les bases par une matrice nulle de la taille

$5e$

montré. ^[5] Votre noyau est complètement

${DisplayStyle V}$

, ta photo

${displayStyle {0_ {w}}}$

Et donc toujours classé

${DisplayStyle 0}$

. Est

${displayStyle v = w}$

, alors l’image zéro est la seule valeurs propres le nombre zéro et l’espace associé est entièrement

${DisplayStyle V}$

.

OperatorNorm [ Modifier | Modifier le texte source ]]

Sont

${DisplayStyle V}$

et

${displayStyle in}$

Chambres normées avec les normes respectives

${displayStyle | cdot | _ {v}}$

et

${displayStyle | cdot | _ {w}}$

, alors la forme d’opérateur de l’image zéro est

${DisplayStyle | non – | = sup _ {| v | _ {v} = 1} | phi (v) | _ {w} = | 0_ {w} | _ {w} = 0}$

.

L’image zéro elle-même prévoit

${displayStyle w = mathbb {r}}$

un demi-standard.

Solution d’équations [ Modifier | Modifier le texte source ]]

En général, l’image zéro résout toute équation d’opérateur linéaire homogène

${displayStyle {Mathcal {l}} u = 0}$

,

par lequel

${displayStyle {Mathcal {l}} dans l (v, w)}$

Un opérateur linéaire est,

${displaystyle u}$

La fonction recherchée et

${DisplayStyle 0}$

La fonction zéro est. Inversement, une équation d’opérateur linéaire inhomogène, dans laquelle le côté droit est inégal de la fonction nulle, n’est jamais résolu par l’image nulle.

Définition [ Modifier | Modifier le texte source ]]

Est

${displaystyle x}$

Beaucoup et

${displaystyle y}$

Un magma avec un, c’est-à-dire beaucoup avec un lien à double chiffre

${displayStyle AST}$

avec un élément neutre

${DisplayStyle 0}$

, alors une image est appelée

${Displaystyle phi colon xto y}$

Zéro illustration si pour tout le monde

${Displaystyle s’il vous plaît x}$

${DisplayStyle phi (x) = 0}$

est applicable. Exemples importants de

${displayStyle (y, ast)}$

sont des monoïdes, des groupes, des anneaux, des modules et – comme dans la section précédente – les salles vectorielles.

Exemples [ Modifier | Modifier le texte source ]]

Caractéristiques [ Modifier | Modifier le texte source ]]

• Martin Barner, Friedrich Flhr: Analyse I . The Gruyter, 2000, ISBN 3-11-016778-6.
• Siegfried Bosch: Algèbre linéaire . Springs, 2009, ISBN 3-540-76437-2.
• Christian Karpfinger, Kurt Meyberg: Algèbre: groupes – anneaux – corps . Springs, 2008, ISBN 3-8274-2018-0.
• Gilbert Strang: Algèbre linéaire . Springs, 2003, ISBN 3-540-43949-8.

1. ↑ Barner, Flori: Analyse I . S. 247 .
2. ↑ Bosch: Algèbre linéaire . S. 78 .
3. ↑ Bosch: Algèbre linéaire . S. 204 .
4. ↑ Bosch: Algèbre linéaire . S. 141 .
5. ↑ Bosch: Algèbre linéaire . S. 93 .
6. ↑ Karpfinger, Meyberg: Algèbre: groupes – anneaux – corps . S. 158 .
7. ↑ Karpfinger, Meyberg: Algèbre: groupes – anneaux – corps . S. 181 .
8. ↑ Karpfinger, Meyberg: Algèbre: groupes – anneaux – corps . S. 172 .