Quickhull – Wikipedia

Foule est un algorithme pour calculer la coquille convexe de toute quantité finie de points dans l’espace bidimensionnel ou tridimensionnel. La couverture convexe d’une quantité de points est décrite par un train polygone fermé, qui représente la connexion de tous les points extrêmes de la foule, comprend ainsi tous les points de la foule. Une explication intuitive fréquemment utilisée de cette coque est une bande de caoutchouc qui couvre la quantité ponctuelle. S’il se trouve serré sur tous les points extérieurs, cela forme la couverture convexe de la file d’attente.
Le nom Foule est dérivé de la similitude avec Quicksort, un algorithme pour trier n’importe quel montant. Il est mentionné pour la première fois dans le livre Géométrie informatique Par Franco Prepared et Michael Shamos, [d’abord] dans lequel les deux auteurs présentent l’algorithme décrit ici, qui ramasse les idées d’autres auteurs. [2] [3] [4]
L’idée algorithmique pour Quickhull provient du principe de «parties et dominantes», qui est souvent utilisée en informatique. Il décrit la procédure pour diviser le problème en plusieurs petits problèmes, puis le résoudre de manière récursive en utilisant le même algorithme. Dans ce contexte, des tentatives sont souvent faites pour choisir la division si intelligemment qu’un grand nombre de quantités de solutions non valides tombent. Ce type de structure peut souvent implémenter des algorithmes qui ont été conçus sur ce principe facilement et facilement lisibles car ils ont une structure récursive compréhensible.
Des noms : S Est le montant des points donnés Skin Est la quantité de points d’un côté du droit à travers les points P et Q . [5]
fonction QuickHull (s)
{ // détermine la coquille convexe de la foule s Coque convexe: = {}
A: = point à l'extrême gauche
B: = point à l'extrême droite
Ajouter les points A et B de la coque convexe
// Celui divise simplement le n - 2 points restants dans les sous-quantités S1 et S2
S1: = quantité de points en s qui se trouvent sur le côté droit de
S2: = quantité de points en s qui se trouvent sur le côté gauche de
Findhull (S1, A, B)
Findhull (S2, B, A)
Édition: coque convexe
} fonction Findhull (SK, P, Q)
{ // détermine les points sur la coquille convexe de la foule s k qui sont sur le côté droit du pq droit Si SK ne contient aucun point alors Édition: coque convexe
C: = le point de SK, qui a la plus grande distance du pq droit
Ajoutez le point C au couvercle convexe entre les points P et Q
// Les trois points P, Q et C divisent les points restants de SK dans les sous-quantités S0, S1 et S2
S0: = les points dans le triangle PCQ
S1: = les points sur le côté droit du PC droit
S2: = les points sur le côté droit du CQ droit
Findhull (S1, P, C)
Findhull (S2, C, Q)
Édition: coque convexe
}

L’algorithme fonctionne sur n’importe quel nombre fini de points. Il n’y a aucune exigence particulière pour l’arrangement ou le nombre de points. Cependant, un arrangement symétrique des points a une plus grande probabilité des meilleurs cas (meilleurs cas) Barrière de temps d’exécution de
Partir et être considérablement plus lent.

Pour déterminer la première division de la foule, les deux points extrêmes de l’axe X sont recherchés. Donc, ces points qui sont les plus à gauche et le plus à droite. Ces points peuvent déjà être ajoutés au train polygone de la coquille convexe, car ils sont garantis pour en faire partie comme des points extrêmes.
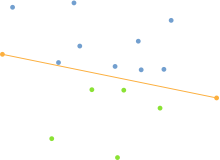
Les deux points trouvés forment une ligne droite qui divise la quantité ponctuelle en deux zones. Tous points liens Beaucoup et tous les points représentent de la ligne droite À droite De l’autre. À droite et liens Dans ce contexte, résulte de l’angle entre le vecteur directionnel de la séparation droite et le vecteur défini par le point de départ du droit et le point à vérifier. Si cet angle est inférieur à 180 °, le point est considéré comme 180 ° comme à gauche que celle de celui-ci.
Les deux sont désormais traités récursivement avec l’algorithme QuickHull par ces points séparés. Dans cet exemple, seule la partie gauche de la quantité de points est prise en compte. Toutes les déclarations faites s’appliquent également équivalentes à la bonne partie.

Le point qui a la distance maximale de la ligne droite est déterminé dans le point de vue considéré. Cela fait évidemment partie du train polygone que vous recherchez. Un triangle est créé avec le point de départ et le point final des lignes droites.

Le triangle est composé de trois points, qui font tous partie des polygones du boîtier convexe. Pour cette raison, tous les points à l’intérieur de ce triangle ne peuvent pas faire partie de ce polygone, car ils sont déjà à l’intérieur. Tous les points de ce triangle peuvent donc être ignorés pour d’autres récursives de l’algorithme.
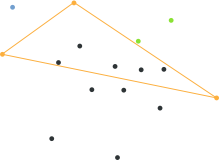
Les lignes droites résultant comme les côtés du triangle sont maintenant considérées comme une ligne de séparation renouvelée de la quantité ponctuelle. Tous les points à gauche du triangle représentent beaucoup, tous les points à droite du triangle l’autre.

Cette division récursive et la détermination des autres points sont répétées jusqu’à ce que le point de départ et le point final de la séparation droite fait partie des quantités à considérer, car dans ce cas, il est clair qu’il s’agit actuellement d’un segment du train polygone que vous recherchez.
- ↑ Franco P. Préparation, Michael Ian Shamos: Géométrie informatique . Une introduction. 1ère édition. Springer-Verlag, 1985, ISBN 0-387-96131-3.
- ↑ William F. Eddy: Un nouvel algorithme convexe de coque pour les ensembles planaires . Dans: Transactions ACM sur les logiciels mathématiques . 3e année, 1977, S. 393–403 .
- ↑ Alex Bykat: Coque convexe d’un ensemble fini de points en deux dimensions . Dans: Lettres de traitement de l’information . 7e année, 1978, S. 296–298 .
- ↑ P. J. Green, B.W. Silverman: Construire la coque convexe d’un ensemble de points dans le plan . Dans: Journal informatique . 22e année, 1979, S. 262–266 .
- ↑ OpenGenus IQ: Algorithme rapide de la coque pour trouver la coque convexe
 Partir et être considérablement plus lent.
Partir et être considérablement plus lent.
Recent Comments