BézieraKrzywa-ウィキペディア、無料百科事典

Posted on June 7, 2023 by lordneo

before-content-x4

ベジエ曲線の例

ベジエカーブ （寸法 /’be.zje.ra/ ） – CAD（微小）エンジニアリング設計プログラムで一般的に使用されるパラメトリック曲線、ベクトルグラフィックスの作成（Corel Draw、Adobe Illustrator、Inkscape）。

after-content-x4

Bézierの曲線は、PierreBézierによって独立して開発されました ^[初め]、フランスのエンジニアルノーとポール・デ・カステルジャウ ^[初め]、競争力のある会社シトロエンで働いています。曲線に関する作業は、1960年代初頭から両方の科学者によって行われましたが、長い間厳格な公式の秘密に覆われていました。ピエール・ベジエの最初の公開が彼の概念を描いたのは1960年代後半までではありませんでしたが、デ・カステルジャウ・シトロエンの作品は数年間隠れていました。 A.R.は、ベジエの曲線の拡散に大きく貢献しました。フォレスト記事 Bezier多項式によるインタラクティブな補間と近似 1972年に業界の手紙「The Computer Journal」で公開されました ^[2]。

Bézier曲線はパラメーター曲線です。つまり、曲線の点の各座標は、実際の数字の特定の関数であり、上記のパラメーターです。平面上の曲線を決定するには、空間の曲線を決定するために2つの機能が必要です。これらの機能のタイプにより、多項式曲線と測定可能な曲線について説明します。コースは、スムーズに接続された多項式または測定可能な曲線の断片で構成される一般的に使用されています。 Bショット曲線（また：滑らかな曲線）。

曲線の種類に関係なく、それはそのコースに影響します 壊れたコントロール 、コントロールポイントによって決定されますが、その数は通常小さいです。この機能は、人間がポイントの位置を自然に決定し、エラーを簡単に修正できるため、インタラクティブな作業を促進します。

14度のマルチマルチベジエ曲線の例

Multi -Curvey 広く使用されています。実際には、少数の制御ポイントで記述されている低い度の曲線が使用されます。最も一般的に使用されるのは、2番目のサイクル曲線（3つの制御ポイント、トルエタイプフォントなど）または3番目のコントロールポイント、たとえば、タイプ1フォント、メタフト、SVG、さまざまなグラフィックパッケージの全範囲）です。より高い程度の曲線の使用頻度は少なくなります。 Multi -Cropsは、OpenGL、Java2d、TCLなど、多くのプログラミングライブラリでも利用できます。低レベルの曲線は、そのような曲線に関連するさまざまなアルゴリズム、たとえば切断、他の曲線との交差点の決定、極端な決定などの実装が容易です。
測定可能な曲がった それらは、多項式曲線よりも1つの基本的な利点があります。それらを使用して、特定の円、楕円、そのクリッピングですべての円錐曲線を表すことができます。これは、コンピューター支援デザインで根本的に重要です。マルチクロップは近似のみが近似できますが、これは、精度が優先事項ではないアプリケーションを描画する際の欠点ではありません。

多項式と測定可能な曲線の両方は、1つの一般的な不便さによって特徴付けられます – 1つの曲線で複雑な形状を提示することは困難です。新しいチェックポイントを追加できることは事実ですが、これは、1つのポイントの変位が曲線全体に影響を与えるため、形状制御が非常に困難であることを意味し、さらに、程度が高いほど、制御ポイントの位置が見えないことを意味します（鮮やかに、長距離にわたって移動する必要があるため、目に見える効果があります）。このため、Bで満たされた曲線が一般的に使用されています。これは、ローカルシェイプコントロールのみを提供し、1つの制御ポイントの変位により密接な環境が変化します。 Bで満たされた曲線は、多項式または測定可能な（比較的低い）曲線の断片で構成される曲線であり、そのような曲線を記述する数学的方程式は、さまざまなフラグメントの接続ポイントで曲線が滑らかになることを保証します。 Nurbsとして知られる測定可能な曲線とBで満たされた表面は、特別な人気を博しました。

Table of Contents

after-content-x4

Multi -Curvey [ 編集 | コードを編集します ]

データはです 制御ポイント

{displaystyle p_ {0}、dots、p_ {n}}

${displaystyle p_{0},dots ,p_{n}}$ 数

{displaystyle n+1。}

${displaystyle n+1.}$

ベジエ曲線の形状は、フィールドが採用された多項式によって記述されています

{displaystyle [0.1]。}

${displaystyle [0,1].}$ 多項式の程度は、コントロールポイントの数に直接依存します – それは

{displaystyle n}

$n$ （コントロールポイント数を引いたもの）。マルチストは通常、バーンスタイン多項式データベースに提示されます ^[初め]（マークされています

{displaystyle b_ {i}^{n}（t）、}

${displaystyle B_{i}^{n}(t),}$ 英文学に携わる

{displaystyle b_ {i、j}（t）}

${displaystyle B_{i,j}(t)}$ ）。バーンスタインベースの多項式は、制御ポイントが当然、そのような多項式の係数であるという意味で便利です – 追加の変換を行う必要はありません。

曲線上の任意のポイントは、依存関係によって説明されます。

{displaystyle p（t）= sum _ {i = 0}^{n} p_ {i} b_ {i}^{n}（t）quad {textrm {dla}} tin [0,1]、}

たとえば、2次元曲線は、一対の多項式によって記述されます。

{displaystyle（x、y）= left（sum _ {i = 0}^{n} x_ {i} b_ {i}^{n}（t）、sum _ {i = 0}^{n} y_ {i} b_ {i}^{n}（t）right）。}

点

{displaystyle P（t）}

$p(t)$ De Casteljauアルゴリズムの使用も見つけることができます。

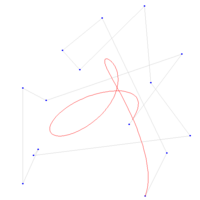
それを作成する2次元ベジエ4度および多項式X（T）およびY（T）の例。コントロールポイントは、バーンスタインベースの多項式の青で灰色のチャートでマークされています。

Bézierのマルチコア曲線の特性：

曲線は、極端なチェックポイントをインターポールします（つまり、 ${displaystyle p（0）= p_ {0}}$
曲線は所有されています 凸シェル 、すなわち ${displaystyletin [0,1]}$
曲線の構造は、アピニカル変換と比較して変化しません。つまり、変換されたチェックポイントから決定される曲線は、この変換後の曲線と同じです。
単一の曲線があります 無限に多い 表現 – 説明されている曲線の場合 ${displaystyle n}$

Bézierの多項式曲線の欠点は、それらを使用して円錐曲線、地区、楕円などを表すことができないことです。この欠陥には、測定可能なBézier曲線が奪われています。

3度目のMulti -Multi Krzywe [ 編集 | コードを編集します ]

3度目のベジエ曲線

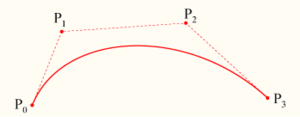
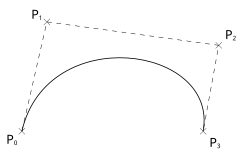
飛行機に横たわっている3度目の曲線が最も頻繁に使用されます。 3度目の曲線を定義すると、4ポイントが決定されます

{displaystyle a、}

$A,$

{displaystyle b、}

$B,$

{displaystyle c}

$C$ 私

{displaystyle d}

$D$ （それに応じて図で

{displaystyle p_ {0}、p_ {1}、p_ {2}、p_ {3}}

$P_{0},P_{1},P_{2},P_{3}$ ）その場所が曲線の経過を決定します。曲線はポイントから始まります

{displaystyle a}

$A$ ポイントに向けられています

{displaystyle B.}

$B.$ それから彼はポイントに向かっています

{displaystyle d}

$D$ ポイントのポイントから到達します

{displaystyle C.}

${displaystyle C.}$ エピソード

{displaystyle {overline {ab}}}

$overline {AB}$ ポイントの曲線に接する

{displaystyle a、}

$A,$ エピソード中

{displaystyle {overline {cd}}}

$overline {CD}$ ポイントでは接線です

{displaystyle d}

$D$

3度目のベジエ曲線は、次の方程式を定義します。

{displaystyle p（t）= a（1-t）^{3}+3bt（1-t）^{2}+3ct^{2}（1-t）+dt^{3} quad {}}

あれは：

{displaystyle p_ {x}（t）= a_ {x}（1-t）^{3}+3b_ {x} t（1-t）^{2}+3c_ {x} t^{2}（1-t）+d_ {x} t^{3}、}、}

{displaystyle p_ {y}（t）= a_ {y}（1-t）^{3}+3b_ {y} t（1-t）^{2}+3c_ {y} t^{2}（1-t）+d_ {y} t^{3}。}。

代替マトリックス録音：

{displaystyle P（t）= left [a、b、c、dright] cdot left [{begin} -1＆3＆-3＆1 \ 3＆-6＆3＆0 \ -3＆3＆0＆0 \ 1＆0＆0＆0＆0END {matrix}}右] {matrix}}右]。}

曲線はポイントから始まります

{displaystyle a}

$A$

{displaystyle（t = 0）}

${displaystyle (t=0)}$ そして、ポイントでの終わり

{displaystyle d}

$D$

{displaystyle（t = 1）。}

${displaystyle (t=1).}$

3度目のベジエ曲線は、次の方程式システムでも説明できます。

{Displaystyle a = (x_ {0}, y_ {0}), b = (x_ {1}, y_ {1}), c = (x_ {2}, y_ {2}), d = (x_ {3}, y_ {3}) {:}}}}}}}}}}}}}}}}}}}}}}}}}}

${displaystyle A=(x_{0},y_{0}),B=(x_{1},y_{1}),C=(x_{2},y_{2}),D=(x_{3},y_{3}){:}}$

{displaystyle x _ {（t）} = a_ {x} t^{3}+b_ {x} t^{2}+c_ {x} t+x_ {0}、}

{displaystyle x_ {1} = x_ {0}+{frac {c_ {x}} {3}}、}

{displaystyle x_ {2} = x_ {1}+{frac {c_ {x}+b_ {x}} {3}}、}

{displaystyle x_ {3} = x_ {0}+c_ {x}+b_ {x}+a_ {x}、}

{displaystyle y _ {（t）} = a_ {y} t^{3}+b_ {y} t^{2}+c_ {y} t+y_ {0}、}

{displaystyle y_ {1} = y_ {0}+{craud {c_ {y}} {3}}、}

{displaystyle y_ {2} = y_ {1}+{craud {c_ {y}+b_ {y}} {3}}、}

{displaystyle y_ {3} = y_ {0}+c_ {y}+b_ {y}+a_ {y}。}

この方法で定義された設計は、方向変数を取得するために逆転させることができます（各ベジエ曲線では一定です）：

{displaystyle c_ {x} = 3（x_ {1} -x_ {0}）、}

{displaystyle b_ {x} = 3（x_ {2} -x_ {1}） – c_ {x}、}

{displaystyle a_ {x} = x_ {3} -x_ {0} -c_ {x} -b_ {x}、}

{displaystyle c_ {y} = 3（y_ {1} -y_ {0}）、}

{displaystyle b_ {y} = 3（y_ {2} -y_ {1}） – c_ {y}、}

{displaystyle a_ {y} = y_ {3} -y_ {0} -c_ {y} -b_ {y}。}

ベジエの測定可能な曲線 [ 編集 | コードを編集します ]

別の記事：ベジエの測定可能な曲線。

ベジエの測定可能な曲線は、平面への均一な座標で定義されたベジエのマルチコア曲線の中央投影です

{distrastaStyle w = 1.}

${displaystyle W=1.}$ 同じことが与えられます

{displaystyle n+1}

$n+1$ チェックポイント。

スペースが均一である場合

{displaystyle k+1}

$k+1$ -inmia、その後、曲線を記述するために非常に多くの多項式が必要です。多項式曲線の任意のポイントは、として与えられます

{displaystyle P（t）=（x（t）、y（t）、dots、w（t））。}

${displaystyle P(t)=(X(t),Y(t),dots ,W(t)).}$ デカルト座標に切り替えた後（ミドルキック

{displaystyle P（t）}

$P(t)$ 飛行機に

{展示w = 1}

$W=1$ ））

{displaystyle k}

$k$ 測定可能な表現、およびこの平面上のポイントにモデルが与えられます

{displaystyle P（t）= left（{frac {x（t）} {w（t）}}}、{frac {y（t）} {w（t）}}、dots右）。}}

${displaystyle p(t)=left({frac {X(t)}{W(t)}},{frac {Y(t)}{W(t)}},dots right).}$

もしも

{displaystyle w（t）= {textrm {const}}}

$W(t)={textrm {const}}$ それは多項式である曲線です – 非公式に言えば、多項式曲線は測定可能な曲線の特別なケースです。

測定可能な曲線の任意のポイントには、パターンが与えられます。

{displaystyle p(t)={frac {sum _{i=0}^{n}w_{i}p_{i}B_{i}^{n}(t)}{sum _{i=0}^{n}w_{i}B_{i}^{n}(t)}}qquad tin [0,1],}

どこ

{displaystylew_ {i}}

$w_{i}$ これは座標ですが、より多くの場合、制御点の制御と呼ばれます。

曲線上のポイントを指定するには、De Casteljauアルゴリズムまたは測定可能または多項式曲線のためにバリアントを使用することもできます。

Bézierの多項式曲線の利点は次のとおりです。

これらはすべての円錐曲線を表すことができます。これは、CADアプリケーションで重要です。
測定可能な曲線の視点投影は常に測定可能な曲線ですが、多項式曲線の視点投影は多項式曲線である必要はありません。これはコンピューターグラフィックスで重要です。
スケール ${displaystylew_ {i}}$

Bで満たされた曲線 [ 編集 | コードを編集します ]

別の記事：B-Shot Curve。

bスタック曲線は、通常は低い多項式または測定可能なベジエ曲線の断片で構成されています

{displaystyle（n）。}

${displaystyle (n).}$ Bで覆われたパラメーター

{displaystylet}

$t$ コンパートメントにも属します

{displaystyle [0.1]。}

${displaystyle [0,1].}$ このコンパートメントはサポートに分割されており、境界線を指定する数字はノードと呼ばれます。 結び目 ）。後続のノードは均等になる可能性があるため、空のサポートを作成します – これは間違いではありません。

ノードがある場合

{displaystyle m+1}

$m+1$

{displaystyle（u_ {0}、dots、u_ {m}）、}

${displaystyle (u_{0},dots ,u_{m}),}$ そして、多項式の程度は等しい

{displaystyle n、}

$n,$ これは、曲線を決定するために必要です

{displaystyle m-n}

$m-n$ チェックポイント、および全体を構成する曲線の数は

{displaystyle m-2n。}

${displaystyle m-2n.}$ 接着曲線は範囲で定義されています

{displaystyle [u_ {n}、u_ {m-n}]、}

${displaystyle [u_{n},u_{m-n}],}$ オンではありません

{displaystyle [0.1]。}

${displaystyle [0,1].}$

B-Zlajana曲線の任意のポイントは、Mansfield-de boora-coxアルゴリズムに起因する特定のパターンです。

{displaystyle p（t）= sum _ {i = 0}^{m-n-1} p_ {i} n_ {i}^{n}（t）quad {textrm {dla}} tin [u_ {n}、u_ {m n}]、}}

どこ

{displaystyle n_ {i}^{n}}

$N_{i}^{n}$ に ナントBスリープ機能 程度

{displaystyle n。}

$n.$

Bで満たされた曲線には、多項式および測定可能な曲線に関連する以下の利点があります。

ローカルシェイプコントロール – 1つの制御点の動きは、せいぜいこの点の小さな環境に影響します ${displaystyle n}$
ノードを配置する可能性は、曲線の形状をより良くより強力に制御できます。さらに、ノードが一致する場合、つまり空のサポートがある場合、「シャープ」（滑らかではない）接続が取得されます。
新しいノードを簡単に挿入できます。 ノット挿入 ）、モデリングプロセスのおかげで簡単です。

Tubility B満たされた曲線（NURB）は、通常の測定可能な曲線と上記の上記の利点を組み合わせて、特別な重要性と人気を獲得しました。

ジェームズd J.D. フォーリージェームズd J.D. 私はイニ、 コンピューターグラフィックスの紹介 、 1月 J. Zabrodzki （翻訳）、ワルシャワ：wydawnictwo naukowo-techniczne、1995、isbn 83-204-1840-2 。
マイケル M. ヤンコフスキーマイケル M. 、 コンピューターグラフィック要素 、ワルシャワ：wydawnictwo naukowo-techniczne、1990、isbn 83-204-1326-5 。
Przemysław P. キシアック Przemysław P. 、 硬化と表面モデリングの基本：コンピューターグラフィックスでの使用 、ワルシャワ：wydawnictwo naukowo-techniczne、2000、isbn 83-204-2464-X 。

after-content-x4

BézieraKrzywa-ウィキペディア、無料百科事典

Multi -Curvey [ 編集 | コードを編集します ]

3度目のMulti -Multi Krzywe [ 編集 | コードを編集します ]

ベジエの測定可能な曲線 [ 編集 | コードを編集します ]

Bで満たされた曲線 [ 編集 | コードを編集します ]

Recent Posts

Recent Comments

Archives

Categories

Meta