積分基準 (それも Maclaurin-Cauchy Integral Starion [初め] ) – 特定の行を積分と比較するという考えに基づいて、ランクの収束の肯定的な単語との収束の基準。この基準の初期の形式は、インドでマダワによって発見されました [2] 14世紀とケララ州の学校の後継者。ヨーロッパでは、1742年にマクラウリンによって再び基準が再び発見されました [3] 私はcauchy’egoです [4] 。
させて
 それは正で減少する機能になります。させて
それは正で減少する機能になります。させて
 すべての人のために
すべての人のために
 その後、シリーズ
その後、シリーズ
|
|
 |
|
(a)
|
それは一致し、積分が間違っている場合にのみ [5]
|
|
 |
|
(私)
|
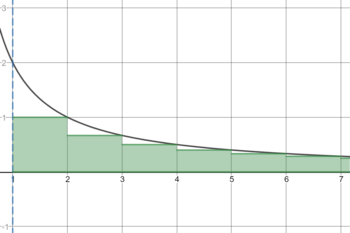
関数のグラフ

コンパートメント内

積分(i)は、曲線下の領域の面積を表現します
 (黒の隣の図)範囲内
(黒の隣の図)範囲内
 シリーズ(a)ポイントのチャートのサイズを与える
シリーズ(a)ポイントのチャートのサイズを与える
 だから彼らは基づいて長方形のフィールドを表現します
だから彼らは基づいて長方形のフィールドを表現します
 そして高さ
そして高さ
 (その隣の図では、緑とマークされています)。したがって、シリーズ(a)の合計は、長方形のフィールドの合計です。これを考慮して、積分基準は次のように解釈できます。チャートの下のフィールドの場合
(その隣の図では、緑とマークされています)。したがって、シリーズ(a)の合計は、長方形のフィールドの合計です。これを考慮して、積分基準は次のように解釈できます。チャートの下のフィールドの場合
 それは終わりました、フィールドの合計はさらに終わりました
それは終わりました、フィールドの合計はさらに終わりました
 (シリーズ(a)の合計に等しい)。 Fr.の各長方形を移動することにより。
(シリーズ(a)の合計に等しい)。 Fr.の各長方形を移動することにより。
 右側に、チャート
右側に、チャート
 コンパートメント内
コンパートメント内
 前述のシフトの図に含まれます。特に、チャートの下のフィールドの場合
前述のシフトの図に含まれます。特に、チャートの下のフィールドの場合
 それは無限であり、また、考慮された図のフィールドにも無限でなければならず、したがって行の合計(a) [6] 。
それは無限であり、また、考慮された図のフィールドにも無限でなければならず、したがって行の合計(a) [6] 。
関数のため
 減少しており、不均一性があります
減少しており、不均一性があります
 ために
ために

 ために
ために

この意味は
-

そしてここから
-

積分(i)が収束している場合、部分積分
-

限られているので、部分的な合計の限られたシーケンスを引き付ける
-

シリーズ(a)。この文字列も非vanishingです(シリーズ(a)の単語が非陰性であると仮定して)。したがって、限られた非vanishの実数の文字列として収束するため、シリーズ(a)は収束します。
シリーズ(a)が収束している場合、部分積分の上記の定義部分も制限されているため、実数の限定的かつ非消化シーケンスとして収束(積分(i)に) [7] 。
-
-

- のために収束します

 それはプラスであり、範囲が減少します
それはプラスであり、範囲が減少します
 したがって、積分基準が使用されます。
したがって、積分基準が使用されます。
-
![{displaystyle int limits _{m}^{infty }{frac {mathrm {d} x}{x^{s}}}=int limits _{m}^{infty }{x^{-s}mathrm {d} x}=left[{frac {x^{-s+1}}{-s+1}}right]_{m}^{infty }=lim _{xto infty }~{frac {x^{-s+1}}{-s+1}}-{frac {m^{-s+1}}{-s+1}}=-{frac {m^{-s+1}}{-s+1}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12d1d309dcff6e58a88dba1ecaa19d38cba32df8)
- いつ
 つまり、いつです
つまり、いつです
 [7] 。
[7] 。
-
-

- のために収束します


我々は持っています
-

-

したがって、不適切な積分
 いつ存在します
いつ存在します
 [8] 。
[8] 。
- ↑ スプルースウッド1966 < 、s。 242。
- ↑ Petrovic 2014↓ 、s。 178。
- ↑ C.マクラウリン、 フラキシオンの論文 、1。エディンバラ、1742。
- ↑ A.L. Cauchy、シリーズの収束について、 完全な作品ser。 2 、7、Gauthier-Villars(1889)、s。 267–279。
- ↑ スプルースウッド1966 < 、s。 243。
- ↑ スプルースウッド1966 < 、s。 244。
- ↑ a b 許可1971↓ 、s。 276。
- ↑ 許可1971↓ 、s。 276–277。

 それは正で減少する機能になります。させて
それは正で減少する機能になります。させて  すべての人のために
すべての人のために  その後、シリーズ
その後、シリーズ 



 (黒の隣の図)範囲内
(黒の隣の図)範囲内  シリーズ(a)ポイントのチャートのサイズを与える
シリーズ(a)ポイントのチャートのサイズを与える  だから彼らは基づいて長方形のフィールドを表現します
だから彼らは基づいて長方形のフィールドを表現します  そして高さ
そして高さ  (その隣の図では、緑とマークされています)。したがって、シリーズ(a)の合計は、長方形のフィールドの合計です。これを考慮して、積分基準は次のように解釈できます。チャートの下のフィールドの場合
(その隣の図では、緑とマークされています)。したがって、シリーズ(a)の合計は、長方形のフィールドの合計です。これを考慮して、積分基準は次のように解釈できます。チャートの下のフィールドの場合  (シリーズ(a)の合計に等しい)。 Fr.の各長方形を移動することにより。
(シリーズ(a)の合計に等しい)。 Fr.の各長方形を移動することにより。  前述のシフトの図に含まれます。特に、チャートの下のフィールドの場合
前述のシフトの図に含まれます。特に、チャートの下のフィールドの場合  減少しており、不均一性があります
減少しており、不均一性があります 











![{displaystyle int limits _{m}^{infty }{frac {mathrm {d} x}{x^{s}}}=int limits _{m}^{infty }{x^{-s}mathrm {d} x}=left[{frac {x^{-s+1}}{-s+1}}right]_{m}^{infty }=lim _{xto infty }~{frac {x^{-s+1}}{-s+1}}-{frac {m^{-s+1}}{-s+1}}=-{frac {m^{-s+1}}{-s+1}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12d1d309dcff6e58a88dba1ecaa19d38cba32df8)

 [7] 。
[7] 。 




Recent Comments