Przybliżenie Kochaski – Wikipedia

W matematyce, Przybliżenie Kochuńskiego Pozwala uzyskać przybliżoną wartość π, zaczynając od konkretnej konstrukcji geometrycznej. Nazwa bierze od jezuitów i matematyka religijnego polskiego Adama Adamandy Kochuńskiego, który po raz pierwszy zaproponował to w swoim traktacie Obserwacje cyklometrycznych w celu ułatwienia praktyki zakwaterowania z 1685 r., Dedykowany problemowi sprostowania obwodu ^{[Pierwszy] [2]} .

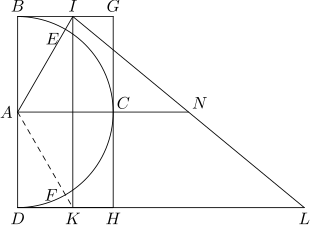
Poniższa konstrukcja jest oryginalną wersją, która pojawia się w traktacie Kochaski i zawiera rozwiązanie problemu naprawienia obwodu jednolitego, poprzez geometryczne określenie segmentu o przybliżeniu długości równej π (tj. Półkulic jednolitego koła).

Zbudowano półkole

${DisplayStyle BCD}$

jednolitego promienia skoncentrowanego

${DisplayStyle A}$

I było napisane w prostokącie

${DisplayStyle Bghd}$

. Weź promień

${DisplayStyle ae}$

które formy w porównaniu do promienia

${DisplayStyle AC}$

kąt

${DisplayStyle 60^{Circ}}$

i przedłużaj go, aż segment zostanie przechwycony

${DisplayStyle BG}$

w momencie

${DisplayStyle i}$

. Wreszcie jest przedłużony

${DisplayStyle DH}$

segmentu

${displayStyle hl}$

długości równej średnicy półkonferencji.

Długość segmentu

${DisplayStyle il}$

Jest to przybliżenie π: w rzeczywistości, jeśli chodzi o

${DisplayStyle il}$

Jak hipotencja trójkąta prostokąta

${DisplayStyle ikl}$

I stosując twierdzenie Pitagorasa, masz to: ^[2]

${displayStyle {begin {wyrównany} il & = {sqrt {ik^{2}+Kl^{2}}} = {sqrt {2^{2}+lewy [po lewej (1-tan {30^{Circ}}} prawy )+2right]^{2}}} \ & = {sqrt {4+lewy (3- {frac {1} {3}} {sqrt {3}} right)^{2}}} = {sqrt {{{{{{{{ frac {40} {3}}-2 {sqrt {3}}}} = 3,141533 … ok. pi .end {wyrównany}}}$

Alternatywna konstrukcja [[[ zmiana |. Modifica Wikitesto ]

Obwód jednolitego promienia skupił się

${DisplayStyle o}$

, a system odniesienia jest zdefiniowany za pomocą osi rzędnych przechodzących przez średnicę pionową i pochodzenie umieszczone w punkcie

${DisplayStyle A}$

. Teraz weź krąg wyśrodkowany

${DisplayStyle A}$

i jednolity promień; Przecina pierwsze koło w punkcie

${DisplayStyle CLEFT (-{frac {sqrt {3}} {2}}, {frac {1} {2}} right)}$

. Włóż okrąg wyśrodkowany

${DisplayStyle C}$

o jednolitym promieniu, który przecina drugi okrąg w punkcie

${DisplayStyle dleft (-{frac {sqrt {3}} {2}},-{frac {1} {2}} right)}$

. Segment, który łączy się

${DisplayStyle o}$

To jest

${DisplayStyle d}$

przecina awarię nieobecności

${DisplayStyle A}$

w momencie

${DisplayStyle eleft (-{frac {sqrt {3}} {3}}, 0right)}$

. Wreszcie punkt jest zbudowany

${DisplayStyle Fleft (3- {frac {sqrt {3}} {3}}, 0right)}$

tak, że jest to zdalnie 3 z

${DisplayStyle d}$

w pozytywnym kierunku odciętej.

Długość segmentu

${DisplayStyle BF}$

Uzyskane z tej konstrukcji geometrycznej jest to przybliżenie wartości π, poprawia do czwartego rysunku dziesiętnego. W rzeczywistości obserwowanie

${DisplayStyle BF}$

Jak hipotencja trójkąta prostokąta

${DisplayStyle BAF}$

I stosując twierdzenie Pitagorasa, masz:

${displayStyle bf = {sqrt {2^{2}+lewy (3- {frac {1} {3}} {sqrt {3}} right)^{2}}} = {sqrt {{frac {40} { 3}}-2 {sqrt {3}}}} = 3 141533 … ok. Pi.}$

^{[3] [4]}