Raport kontraktowy – Wikipedia

Posted on August 1, 2022 by lordneo

before-content-x4

W matematyce, dokładniej w teorii zamówień, jeden zamówienie całości jest binarna relacja między elementami należącymi do całości, która cieszy się następującymi właściwościami:

after-content-x4

Definiuje siebie Razem częściowo zamówiono (Lub zamówienie ) Para składająca się z całości i relacji zamówień. Relacje zamówień są często wskazywane z symbolami

{DisplayStyle Leq}

$leq$ W

{DisplayStyle Subteteq}

$subseteq$ W

{DisplayStyle SqSubseteq}

$sqsubseteq$ To jest

{DisplayStyle Preccurlyeq}

$preccurlyeq$ .

W języku angielskim jest również częściowo uporządkowany zestaw poset ( Częściowo zamówiony zestaw ), a ten termin jest używany również w języku włoskim.

Podaj dwa zestawy

after-content-x4

{DisplayStyle A}

$A$ To jest

{DisplayStyle B}

$B$ , ich kartezjański produkt to zestaw uporządkowanych par zdefiniowanych w następujący sposób: ^[Pierwszy]

m Omów ten Slepleyimimate:.

Jest zdefiniowany jako związek binarny w całości

{DisplayStyle A}

$A$ podzbiór

{DisplayStyle r}

$R$ kartezjański produkt

{DisplayStyle Atimes a}

$Atimes A$ . ^[2]Dwa elementy

{DisplayStyle x}

$x$ To jest

{DisplayStyle y}

$y$ są powiązane z

{DisplayStyle r}

$R$ SE:

{displayStyle (x, y) w r}

I w tym przypadku jest napisane

{DisplayStyle xry}

${displaystyle xRy}$ .

Związek zamówienia

{DisplayStyle Leq}

$leq$ Jest to binarny związek między elementami całości

{DisplayStyle A}

$A$ Refleksyjny, antyanimalny i przechowywany. ^[3]

Już wyraźnie ten raport spełnia następujące nieruchomości:

{DisplayStyle xleq xquad forall xin a}

{DisplayStyle [xleq yland yleq x] implikuje x = yquad forall x, yin a}

{TextStyle [xleq yland yleq z] implikuje xleq zquad forall x, y, zin a}

Relacje zamówień są często wskazywane z symbolami

{DisplayStyle Leq}

$leq$ W

{DisplayStyle Subteteq}

$subseteq$ W

{DisplayStyle SqSubseteq}

$sqsubseteq$ To jest

{DisplayStyle Preccurlyeq}

$preccurlyeq$ .

Para

{displayStyle (a, leq)}

$(A,leq )$ składający się z całości i relacji z zamówieniem Razem częściowo zamówiono lub po prostu zamówienie , nie należy mylić z bardziej konkretnym terminem całkowicie uporządkowanym razem.

Table of Contents

Pierwsze przykłady [[[ zmiana |. Modifica Wikitesto ]

Dobrze znane przykłady częściowo uporządkowanych zestawów to:

Każda rodzina zestawów wyposażona w związek włączenia

{DisplayStyle Arbleftrightarrow Asubseteq B}

$aRbLeftrightarrow asubseteq b$ (Znaczy co

{DisplayStyle A}

$a$ jest podzbiorem

{DisplayStyle B}

$b$ )

Niektórzy autorzy ^[4]definiują jako „wąski” raport zamówienia

{displayStyle (a, <)}

${displaystyle (A,<)}$ który spełnia właściwości antyrefleksyjne, anty -medialne i przechodnie (lub, równoważnie i bardziej zwięźle, asymetryczne i przechodnie), a zatem powiedzenie zamówienia „Zakon”

{displayStyle (a, leq)}

${displaystyle (A,leq )}$ . Bliski porządek ma na celu skupienie się na asymetrii związku, nie biorąc pod uwagę refleksyjności.

Chociaż te dwie definicje są odrębne, ich badanie nie wykazuje poważnych różnic, ponieważ między dwiema klasami relacji istnieje bardzo prosta korespondencja biuniwokalna.

Jest

{DisplayStyle A}

$A$ całość i oznacza

{DisplayStyle, Delta (a)}

${displaystyle ,Delta (A)}$ przekątna

{DisplayStyle, Atimes a}

${displaystyle ,Atimes A}$ , Znaczy co

{DisplayStyle Delta (a): = {(x, x): proszę o}}

${displaystyle Delta (A):={(x,x):xin A}}$ , potem do każdego związku z szerokim rzędem

{displayStyle (a, leq)}

${displaystyle (A,leq )}$ Związek o bliskiej kolejności jest powiązany

{DisplayStyle (a, leq) setMinus delta (a)}

${displaystyle (A,leq )setminus Delta (A)}$ ; odwrotnie do każdego związku z bliskim zamówieniem

{displayStyle (a, <)}

${displaystyle (A,<)}$ Związek szerokiego rzędu jest powiązany

{DisplayStyle (a, <) cup delta (a)}

${displaystyle (A,<)cup Delta (A)}$ .

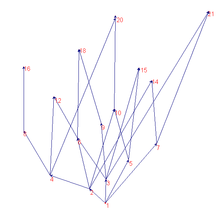
Jeśli całość

{DisplayStyle A}

$A$ Zależność zamówienia może być reprezentowana lub ponumerowana może być wizualnie za pośrednictwem digrafa (rep.

{DisplayStyle A}

$A$ I tak, że dwa węzły

{DisplayStyle A}

$a$ To jest

{DisplayStyle B}

$b$ są połączone łukiem, jeśli i tylko jeśli

{DisplayStyle Aleq B}

$aleq b$ I nie ma między nimi żadnych elementów pośrednich (to znaczy nie ma

{DisplayStyle cneq a, b}

$cneq a,b$ tak, że

{DisplayStyle Aleq C}

$aleq c$ To jest

{DisplayStyle Cleq B}

$cleq b$ ). Wykres relacji zamówienia nie może mieć cykli, podczas gdy może mieć wiele połączonych komponentów, a dowolna liczba łuków może wejść i wyjść i wyjść. Jeśli wykres jest ponumerowany, nieskończone łuki mogą wejść, wyjść, wyjść lub wyjść (tak jest w przypadku raportu podziału).

Dwa elementy

{DisplayStyle A}

$a$ To jest

{DisplayStyle B}

$b$ częściowo zamówionego zestawu

{DisplayStyle, (a, leq),}

${displaystyle ,(A,leq ),}$ Mówią, że oni porównywalny Jeśli tak się stanie

{DisplayStyle Aleq B}

$aleq b$ albo to

{DisplayStyle Bleq a}

$bleq a$ .

Ogólnie rzecz biorąc, dwa elementy relacji częściowego rzędu mogą nie być porównywalne, to znaczy niekoniecznie są ze sobą. Na przykład w

{DisplayStyle Mathbb {n} backslash {0}}

${mathbb N}backslash {0}$ Wyposażone w raport z podziału, elementy 2 i 3 nie są powiązane, ponieważ żaden z nich nie jest partycją drugiego.

Mówi się, że całość jest prosta kolejność O liniowy , Lub Całkowite zamówienie Jeśli dla każdego

{DisplayStyle A, bin a}

$a,bin A$ W

{DisplayStyle A}

$a$ To jest

{Styl tekstowy B}

${textstyle b}$ Są porównywalne (tj. Warto

{DisplayStyle Aleq B}

$aleq b$ Lub

{DisplayStyle Bleq a}

$bleq a$ ).

Digrafh całkowicie uporządkowanego zestawu może być reprezentowany jako segment lub linia prosta lub półmeretta, na której leżą wszystkie węzły (odpowiadające wszystkim elementom całości).

Być zamówieniem

{displayStyle (a, leq)}

$(A,leq )$ , mówi się łańcuch Każdy podzbiór

{DisplayStyle ysubseteq a}

${displaystyle Ysubseteq A}$ tak, że związek zmniejszonego rzędu do

{DisplayStyle y}

$Y$ Stanowi to proste zamówienie.

Zamiast tego mówi się antyczny całego częściowo zamówionego

{displayStyle (a, leq)}

$(A,leq )$ podzbiór

{DisplayStyle ysubseteq a}

${displaystyle Ysubseteq A}$ którego elementy są niezaprzeczalne. Zabytkowa częściowo uporządkowanego zestawu podziału jest dostarczany przez zestaw liczb pierwszych.

Przykład [[[ zmiana |. Modifica Wikitesto ]

W przypadku częściowo uporządkowanego zestawu podzielności zestawy dodatnich mocy pierwszej liczby, a bardziej ogólnie podgrupy uzyskane z procesem, który rozpoczyna się, który rozpoczyna cały dodatni i kontynuuje poprzez dodanie wielu dodanych wcześniej dodanych do procesu. Można rozważyć skończone lub nieskończone łańcuchy; Poprzedni proces może być zakończony lub nieograniczony.

Jest

{displayStyle (a, leq)}

$(A,leq )$ Zamówienie (post) e

{DisplayStyle VAPTYSET NEQ SSUBSETEQ A}

${displaystyle emptyset neq Ssubseteq A}$ . Wtedy mówi się, że element jest

{DisplayStyle yin a}

${displaystyle yin A}$ to jest kurtka Z

{DisplayStyle s}

$S$ samego siebie

{DisplayStyle Forall Xin S, xleq y}

$forall xin S, xleq y$ .

Podobnie, w podwójny sposób, element

{DisplayStyle yin a}

${displaystyle yin A}$ Jest zdefiniowany jako górnictwo całości

{DisplayStyle s}

$S$ samego siebie

{DisplayStyle Forall Xin S, Yleq X}

$forall xin S, yleq x$ .

{DisplayStyle s}

$S$ Przyznaje przynajmniej marjoraranta (wydobycie), a potem tak się mówi

{DisplayStyle s}

$S$ Jest to ograniczony podzbiór powyżej (poniżej).

Podzbiór, który ma zarówno hałas, jak i wydobycie, mówi Ograniczone zamówienie .

Jeśli całość

{DisplayStyle s}

$S$ Jest to zestaw liczbowy o kardynałach większy niż jeden (

{DisplayStyle | s |> 1}

$|S|>1″></span>) Następnie wybór jego podzbioru <span class=$

{DisplayStyle S_ {2} Subteteq s}

$S_{2}subseteq S$ z kardynałem równą 2 (

{DisplayStyle | S_ {2} | = 2}

$|S_{2}|=2$ ), można zdefiniować minimum między jedynymi dwoma elementami,

{DisplayStyle A}

$a$ To jest

{DisplayStyle B}

$b$ Z następującym raportem:

{DisplayStyle Min {A, B} = Mathbf {1} _ {Mathbb {r} ^{-}} (a-b) cdot (a-b)+b}

Maksimum między dwoma elementami jest zamiast tego z następującym wyrażeniem

{DisplayStyle Max {a, b} = Mathbf {1} _ {Mathbb {r} ^{+}} (a-b) cdot (a-b)+b}

Gdzie z

{DisplayStyle Mathbf {1}}

${displaystyle mathbf {1} }$ Tak i wskazałem funkcję orientacyjną.

Maksymalne i minimalne elementy [[[ zmiana |. Modifica Wikitesto ]

Jest

{displayStyle (a, leq)}

$(A,leq )$ porządek. Mówi się, że

{DisplayStyle M}

$m$ To jest Minimalny element Z

{DisplayStyle A}

$A$ samego siebie

{DisplayStyle forall Ain A, Mleq A}

${displaystyle forall ain A, mleq a}$ .

Definiuje siebie maksymalny element Z

{DisplayStyle A}

$A$ I

{DisplayStyle yin a}

$yin A$ tak, że

{DisplayStyle forall Ain A, Aleq y}

${displaystyle forall ain A, aleq y}$ .

Istnieją systemy, dla których nie ma minimalnego elementu (odpowiednio maksimum); Łatwo pokazuje, że jeśli ma minimalny element (odpowiednio maksimum), jest wyjątkowy. Kiedy istnieją, maksymalny element i minimalny element

{DisplayStyle A}

$A$ Są one odpowiednio wskazane, jak Max

{DisplayStyle A}

$A$ To jest min

{DisplayStyle A}

$A$ .

W przypadku zamówień bezżsamowych warto zdefiniować dwie inne pojęcia: element minimalny i maksymalny.

${DisplayStyle M}$

${DisplayStyle M}$

Ogólnie rzecz biorąc, maksymalny i maksymalny element nie odpowiadają temu samemu elementowi. Rozważ jako przykład całość

{DisplayStyle {2,3,4,5,6}}

${2,3,4,5,6}$ dostarczone z raportem podziału: nie przyznaje się do maksimum ani minimum, ale na przykład 3 jest minimalnym elementem

{DisplayStyle x | 3}

$x|3$ Jest zadowolony tylko dla

{DisplayStyle x = 3}

$x=3$ . Zapłacono również, że element 3 nie może być maksymalny. Jeśli tak, to 3 nie podzieliłoby żadnego innego elementu całości, ale

{DisplayStyle 3 | 6}

$3|6$ co pokazuje absurdalność twierdzenia

{DisplayStyle 3Neq 6}

$3neq 6$ . Nawet 5 jest zarówno maksymalnym, jak i minimalnym elementem, ponieważ nie jest związany z żadnym innym elementem zestawu różnego od siebie. Z przykładu łatwo zgadnąć, że dwie definicje (maksymalny i maksymalny element; minimalny i minimalny element) pokrywają się w obecności prostej kolejności.

Lepsze i niższe ekstremalne [[[ zmiana |. Modifica Wikitesto ]

Jest

{displayStyle (a, leq)}

$(A,leq )$ zamówienie i być

{DisplayStyle VAPTYSET NEQ SSUBSETEQ A}

${displaystyle emptyset neq Ssubseteq A}$ . Definiujemy:

{DisplayStyle m_ {s} = {xin a, |, {x}; {is}; {Marjorante}; {of}; s}}}

${displaystyle M_{S}={xin A,|,{x};{e'};{maggiorante};{di};S}}$ ;

{DisplayStyle m_ {s} = {a, |, {x}; {e ‘}; {mindleante};

${displaystyle m_{s}={xin A,|,{x};{e'};{minorante};{di};S}}$ .

Następnie definiują siebie:

Wyższa skrajność ${DisplayStyle s}$

niższa skrajność ${DisplayStyle s}$

Zauważamy, że biorąc pod uwagę podzbiór, nie mówi się, że przyznaje się do minimum lub maksimum, a zatem nie mówi się, że istnieją wyższe i dolne skrajności.

Segmenty początkowe i końcowe [[[ zmiana |. Modifica Wikitesto ]

Jest

{displayStyle (a, leq)}

$(A,leq )$ Zestaw uporządkowany i podzbiór

{DisplayStyle ssubseteq a}

${displaystyle Ssubseteq A}$ , W tym czasie

{DisplayStyle s}

$S$ i powiedział:

Innymi słowy, elementy

{DisplayStyle s}

$S$ Nie przyznają (odpowiednio) minimum ani maksymalnie na zewnątrz

{DisplayStyle s}

$S$ .

Związek zamówienia w całości

{DisplayStyle A}

$A$ Mówi się „dobrze założone” lub dobre zamówienie, jeśli każda podzbiór

{DisplayStyle y}

$Y$

{DisplayStyle Subteteq}

$subseteq$

{DisplayStyle A}

$A$ Non -pusty jest wyposażony w minimum.

Typowy przykład Dobry system To właśnie określa standardowy związek zamówienia

{DisplayStyle Mathbb {n}}

$mathbb N$ liczb naturalnych. Afirmacja, że Naturals to dobrze uporządkowany zestaw, a mianowicie każdy podzbiór

{DisplayStyle x}

$X$ Z

{DisplayStyle Mathbb {n}}

$mathbb N$ Ma minimum, czasami nazywany jest zasadą dobrego porządku i można go wykazać równoważnie zasadzie indukcji.

Twierdzenie o dobrych zamówieniach [[[ zmiana |. Modifica Wikitesto ]

Twierdzenie o dobrej kolejności (nie mylą się z zasadą dobrego porządku) zapewnia, że na każdym zbiorze nieudkowym można go zdefiniować jako dobrze uznaną relację (lub dobry system). To stwierdzenie jest równoważne z wybranym aksjomatem (tj. Zakładając, że jest to prawda, aksjomat wyboru i odwrotnie można wykazać).

Produkt kartezjański dwóch częściowo uporządkowanych zestawów może być również wyposażony w zamówienie na kilka sposobów:

Zgodnie z porównaniem „terminu terminu” ${displayStyle (a_ {1}, b_ {1}) leq (a_ {2}, b_ {2})}$

Według raportu ${displayStyle (a_ {1}, b_ {1}) leq (a_ {2}, b_ {2})}$

Jeśli oba zamówienia są proste, porządek leksykograficzny jest również, ale niekoniecznie pozostałe dwa.

Oni są

{displayStyle (a, leq)}

${displaystyle (A,leq )}$ To jest

{displayStyle (p, preccurlyeq)}

$(P,preccurlyeq)$ dwa zamówienia i być

{DisplayStyle fcolon ato p}

${displaystyle fcolon Ato P}$ .

{DisplayStyle f}

$f$ mówi się monotonny samego siebie

{DisplayStyle xleq yrightarrow f (x) preccurlyeq f (y)}

$x leq y Rightarrow f(x) preccurlyeq f(y)$ Dla każdego x, y w

{DisplayStyle P}

$P$ .

{DisplayStyle f}

$f$ mówi się Antitona samego siebie

{DisplayStyle xleq yrightarrow f (x) sccurlyeq f (y)}

$x le y Rightarrow f(x) succcurlyeq f(y)$ Dla każdego x, y w

{DisplayStyle P}

$P$ .

^ Reed, Simon, Pag. 1 .
^ Reed, Simon, Pag. 2 .
^ Reed, Simon, Pag. 3 .
^ Vincenzo Aversa, Metody ilościowe decyzji. Algebra i analiza podstawowa w wyborze problemów z wyborem , W Podręczniki dla uniwersytetu , Liguori Editore, 2000, s. 12-15, ISBN 9788820731649.

Michael Reed, Barry Simon, Metody współczesnej fizyki matematycznej, t. 1: Analiza funkcjonalna , 2ª ed., San Diego, Kalifornia, Academic Press Inc., 1980, ISBN 0-12-585050-6

after-content-x4

Raport kontraktowy – Wikipedia

Pierwsze przykłady [[[ zmiana |. Modifica Wikitesto ]

Przykład [[[ zmiana |. Modifica Wikitesto ]

Maksymalne i minimalne elementy [[[ zmiana |. Modifica Wikitesto ]

Lepsze i niższe ekstremalne [[[ zmiana |. Modifica Wikitesto ]

Segmenty początkowe i końcowe [[[ zmiana |. Modifica Wikitesto ]

Twierdzenie o dobrych zamówieniach [[[ zmiana |. Modifica Wikitesto ]

Recent Posts

Recent Comments

Archives

Categories

Meta