Algorytm de Ford-Fulkeson-Wikipédia

Przykład wykonania algorytmu Forda-Fulkerson. Animacja wyświetla wykres resztkowy odpowiadający każdej iteracji.

W informatyce, Algorytm Forda-Fulkerson jest algorytmem problemu maksymalnego przepływu, klasycznego problemu optymalizacji w dziedzinie badań operacyjnych. Jest to spowodowane Lester Randolph Ford Junior i D. R. Fulkerson ^{[[[ Pierwszy ]} I jest to wariant algorytmu Busackera i Gowen.

Definicja problemu [[[ modyfikator |. Modyfikator i kod ]

Ten problem optymalizacji może być reprezentowany przez wykres z wejściem (po lewej) i wyjściem (po prawej). Przepływ reprezentuje krążenie wejścia do wyjścia, stąd użycie tego algorytmu w problemach sieciowych. Aplikacje są wiele: problemy komputerowe, drogi, koleje itp. Dotyczy to również wszystkich innych problemów transferowych, takich jak import/eksport, migracyjne, przepływy demograficzne, ale także na przepływach czysto cyfrowych, takich jak transfery finansowe. W przypadku bardzo dużych danych istnieje kilka bardziej wydajnych algorytmów do rozwiązania problemu maksymalnego przepływu.

Przykład aplikacji [[[ modyfikator |. Modyfikator i kod ]

Firma towarowa ma trzy centra: jeden w Paryżu, drugi w Lyonie, trzeci w Marsylii. Możliwe są trzy miejsca: Polska, Szwecja, Grecja. Każde z centrów towarowych ma początkowe zapasy towarów (Paryż: 100; Lyon: 80; Marsylia: 150). Podobnie każdy kraj przybycia ma maksymalne żądanie importu (Polska: 120; Szwecja: 140; Grecja: 50).

Algorytm Forda-Fulkerson zoptymalizuje te przepływy za pomocą narzędzia do modelowania matematycznego. Podstawowa struktura jest reprezentowana przez zorientowany wykres, którego po lewej stronie symbolizuje początkowy zapas. Trzy łuki odchodzą, każde prowadzące do szczytu reprezentującego centrum towarowe. Ostatni szczyt symbolizuje koniec dostawy, do którego trzy łuki pochodzą ze szczytów reprezentujących cel dostawy.

W niniejszym przykładzie macierz sąsiedniej przenosi zatem w pierwszym wierszu wartości wspomnianych zapasów. I odwrotnie, pod koniec łańcucha powiązana macierz uwzględni w ostatniej kolumnie odpowiednie żądania cytowanych krajów. Pomiędzy szczytami „centrum towarowego” a „docelowym” szczytami można znaleźć na szczytach i pośrednie łuki, pojemności tych łuków odpowiadające maksymalnej frachcie od jednego punktu do drugiego.

Paris Polska
           / /
    100 --- ------- ... ------- ---- 120
       / 80 węzłów 140
Wyjazd ------- Lyon ----- Intermé- ---- Szwecja -------- End
                          Pamiętniki /
    150 --- ------- ... ------- --- 50
                  / /
           Marsylia Grecja 

Problem można uogólnić na krążenie w sieci (pojazdy, płyny, pieniądze itp.), Ilości matematyczne bezkrytycznie zastępują rzeczywiste fakty, które mają reprezentować.

Formalizowanie [[[ modyfikator |. Modyfikator i kod ]

Sieć [[[ modyfikator |. Modyfikator i kod ]

Lub sieć

z :

• 
  ${displayStyle (s, a)}$

  wykres zorientowany na niezaprzeczalny;

• pojemność
  ${DisplayStyle C: Arightarrow Mathbb {N} ^{Star}}$

  Z konwencją: jeśli łuk

  ${displayStyle (u, v)}$

  nie istnieje,

  ${DisplayStyle C (u, v) = 0}$

  ;

• ŹRÓDŁO S Sans Arcs uczestnicy;
• Studnia T Bez wychodzących łuków.

Zakłada się, że nie ma anty-równoległych łuków, to znaczy, że istnienie łuku

wyklucza istnienie ARC

.

Ładny [[[ modyfikator |. Modyfikator i kod ]

Przepływ sieci jest funkcją

Kto sprawdza:

• Dla wszystkich szczytów
  ${displayStyle (u, v) instimes s}$

  , na

  ${DisplayStyle 0leq f (u, v) leq c (u, v)}$

  ;

• na każdy szczyt
  ${DisplayStyle uin s}$

  Jak na przykład

  ${DisplayStyle Uneq s}$

  I

  ${DisplayStyle Uneq t}$

  :

  $m Slave Eble State Pever State Emb) Tume (din)) quis mama mé) m rebine))$

  (Przychodzący przepływ jest równy przepływowi wychodzącemu: właściwość ochrony).

Wartość przepływu F Wschód

.

Jest to algorytm iteracyjny.
Z każdą iteracją obecne rozwiązanie jest przepływem, który spełnia ograniczenia pojemności (jest to zatem możliwy do osiągnięcia przepływ), a algorytm próbuje zwiększyć wartość tego przepływu.
Może to wymagać anulowania niewłaściwych wyborów. Aby to zrobić, definiujemy resztkowy wykres G i F co wskazuje możliwe modyfikacje (dodanie lub anulowanie): jest to wykres ważony

gdzie mamy

I

Pseudo kod [[[ modyfikator |. Modyfikator i kod ]

 Wejście Sieć ${DisplayStyle g = (s, a, c, s, t)}$ Wyjście Maksymalny przepływ F  Funkcjonować Ford_fulkerson ( ${DisplayStyle g}$) ${DisplayStyle Fleftarrow}$Ładne zero Dopóki Istnieje prosta ścieżka ${DisplayStyle Gamma}$z S ma T Na wykresie resztkowym ${DisplayStyle r_ {f}}$: ${DisplayStyle delta = min {r_ {f} (u, v) :( u, v) w gamma}}$ Dla cała krawędź ${DisplayStyle (u, v) w gamma}$: I  ${displayStyle (u, v) w a}$: ${DisplayStyle f (u, v): = f (u, v)+delta}$ W przeciwnym razie : ${DisplayStyle f (v, u): = f (v, u) -Delta}$ Odrzucać  F  

Algorytm nie określa, jak znaleźć każdą ścieżkę

. Algorytm Edmonds-Karp, specjalizacja algorytmu Forda-Fulkersona, oferuje trasę szerokości.

Każda znaleziona ścieżka ma gwarancję zwiększenia wartości przepływu, ponieważ koniecznie zaczyna się od łuku opuszczającego lato źródła i kończy się łukiem, który dobrze wpisuje się na szczyt.

Przykład wykonania [[[ modyfikator |. Modyfikator i kod ]

Rozważamy sieć przepływu ${DisplayStyle g = (s, a, c, s, t)}$ , składający się z wykresu ${displayStyle (s, a)}$ na czterech szczytach ${DisplayStyle s = {s, t, u, v}}$ i pięć krawędzi ${DisplayStyle a = {(s, u), (u, t), (s, v), (v, t), (u, v)}}$ , ze źródła ${DisplayStyle sin s}$ , Wellsa ${DisplayStyle Tin S}$ i funkcja pojemności ${DisplayStyle Ccolon ATO Mathbb {R} _ {Geq 0}}$ . Zaczynamy od pustego przepływu ${DisplayStyle f}$ wartość ${DisplayStyle 0}$ Każda krawędź. Początkowo wykres resztkowy ${DisplayStyle G_ {f}}$ i resztkowe zdolności ${DisplayStyle r_ {f}}$ Następnie odpowiadają dokładnie sieci ${DisplayStyle g}$ z pojemnością ${DisplayStyle C}$ .	Wykres ${DisplayStyle g}$ (z pojemnością ${DisplayStyle C}$ )		${displaystyle ein A}$ ${displaystyle c(e)}$ ${displaystyle (s,u)}$ 4 ${displaystyle (u,t)}$ Pierwszy ${displaystyle (s,v)}$ 2 ${displaystyle (v,t)}$ 6 ${displaystyle (u,v)}$ 3
	Ładny ${DisplayStyle f}$		${displaystyle ein A}$ ${displaystyle f(e)}$ ${displaystyle (s,u)}$ 0 ${displaystyle (u,t)}$ 0 ${displaystyle (s,v)}$ 0 ${displaystyle (v,t)}$ 0 ${displaystyle (u,v)}$ 0
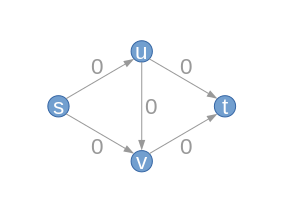	Resztkowy wykres ${DisplayStyle G_ {f}}$ (Z resztkową pojemnością ${DisplayStyle r_ {f}}$ )		${displaystyle ein A}$ ${displaystyle r_{f}(e)}$ ${displaystyle r_{f}({overleftarrow {e}})}$ ${displaystyle (s,u)}$ 4 0 ${displaystyle (u,t)}$ Pierwszy 0 ${displaystyle (s,v)}$ 2 0 ${displaystyle (v,t)}$ 6 0 ${displaystyle (u,v)}$ 3 0
Załóżmy, że algorytm najpierw wybiera ścieżkę ${DisplayStyle gamma = lewy ((s, u), (u, v), (v, t) po prawej)}$ (niebieski). Na tej ścieżce możesz jak najwięcej zwiększyć natężenie przepływu ${DisplayStyle 3}$ Od grzbietu ${displayStyle (u, v)}$ ogranicza ( ${DisplayStyle r_ {f} ((u, v)) = 3}$ ). Rezultatem jest nowy przepływ (który zawsze będzie nazywany ${DisplayStyle f}$ ) z ${DisplayStyle f ((s, u)) = f ((u, v)) = f ((v, t)) = 3}$ . Grzbiet ${displayStyle (s, u)}$ ma pojemność ${DisplayStyle C ((s, u)) = 4}$ . Jest używany w przepływie: ${DisplayStyle f ((s, u)) = 3}$ . Na wykresie resztkowym jego pojemność resztkowa będzie zatem ${DisplayStyle r_ {f} ((s, u)) = c ((s, u))-f ((s, u)) = 1}$ . Podobnie ${DisplayStyle r_ {f} ((u, v)) = c ((u, v))-f ((u, v)) = 3-3 = 0}$ I ${DisplayStyle r_ {f} ((v, t)) = c ((v, t))-f ((v, t)) = 6-3 = 3}$ . Trzy krawędzie ${DisplayStyle (s, u), (u, v), (v, t)}$ są ściśle pozytywne w przepływie. Te wagi przepływu mogą nie być najbardziej optymalne. Nowe tylne krawędzie ${displayStyle (t, v), (v, u), (u, s)}$ (na czerwono) na wykresie resztkowym zaznacz fakt, że zawsze możemy zmniejszyć przepływ tych krawędzi.	Poprawa ścieżki ${DisplayStyle Gamma}$ (Z resztkowymi zdolnościami 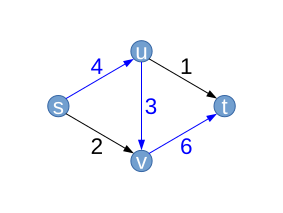${DisplayStyle r_ {f}}$ )
	Ładny 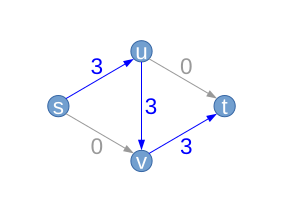${DisplayStyle f}$		${displaystyle ein A}$ ${displaystyle f(e)}$ ${displaystyle (s,u)}$ 3 ${displaystyle (u,t)}$ 0 ${displaystyle (s,v)}$ 0 ${displaystyle (v,t)}$ 3 ${displaystyle (u,v)}$ 3
	Resztkowy wykres ${DisplayStyle G_ {f}}$ wynikowe (z nowymi możliwościami resztkowymi 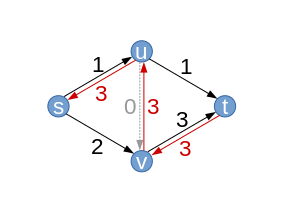${DisplayStyle r_ {f}}$ )		${displaystyle ein A}$ ${displaystyle r_{f}(e)}$ ${displaystyle r_{f}({overleftarrow {e}})}$ ${displaystyle (s,u)}$ Pierwszy 3 ${displaystyle (u,t)}$ Pierwszy 0 ${displaystyle (s,v)}$ 2 0 ${displaystyle (v,t)}$ 3 3 ${displaystyle (u,v)}$ 0 3
Załóżmy, że algorytm wybiera poprawę ścieżki ${DisplayStyle gamma = ((s, v), (v, u), (u, t))}$ . Maksymalny wzrost przepływu jest ograniczony przez pojemność resztkową ${DisplayStyle r_ {f} ((u, t)) = c ((u, t))-f ((u, t)) = 1-0 = 1}$ . Po raz pierwszy przechodzimy przez tylną krawędź ( ${displayStyle (v, u)}$ ). Podczas przepływu F Zwiększa 1 wzdłuż krawędzi (S, V) I (u, t) , zmniejsza się o 1 wzdłuż (u, v) . Można zauważyć, że resztkowe pojemności tylnych krawędzi są zawsze równe ciężarowi przepływu.	Poprawa ścieżki ${DisplayStyle Gamma}$ (Z resztkowymi zdolnościami 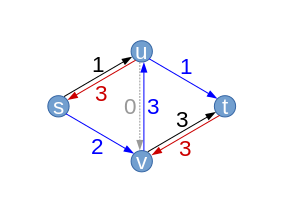${DisplayStyle r_ {f}}$ )
	Ładny 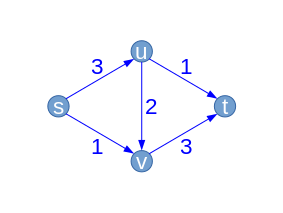${DisplayStyle f}$		${displaystyle ein A}$ ${displaystyle f(e)}$ ${displaystyle (s,u)}$ 3 ${displaystyle (u,t)}$ Pierwszy ${displaystyle (s,v)}$ Pierwszy ${displaystyle (v,t)}$ 3 ${displaystyle (u,v)}$ 2
	Resztkowy wykres ${DisplayStyle G_ {f}}$ wynikowe (z nowymi możliwościami resztkowymi 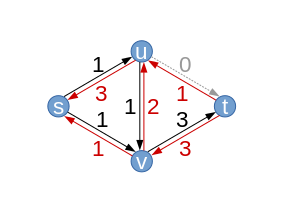${DisplayStyle r_ {f}}$ )		${displaystyle ein A}$ ${displaystyle r_{f}(e)}$ ${displaystyle r_{f}({overleftarrow {e}})}$ ${displaystyle (s,u)}$ Pierwszy 3 ${displaystyle (u,t)}$ 0 Pierwszy ${displaystyle (s,v)}$ Pierwszy Pierwszy ${displaystyle (v,t)}$ 3 3 ${displaystyle (u,v)}$ Pierwszy 2
Załóżmy, że algorytm ponownie wybiera ścieżkę ${DisplayStyle gamma = lewy ((s, u), (u, v), (v, t) po prawej)}$ . Tym razem przepływ wzdłuż ścieżki można zwiększyć tylko o 1. To dokładnie odpowiada ilości, o którą zmniejszyliśmy (u, v) w poprzednim kroku. Rzeczywiście, algorytm może zrobić wiele tam iz powrotem.	Poprawa ścieżki ${DisplayStyle Gamma}$ (Z resztkowymi zdolnościami 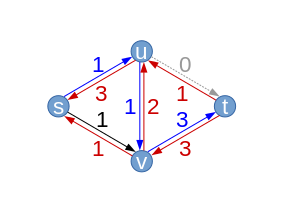${DisplayStyle r_ {f}}$ )
	Ładny 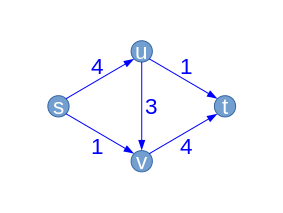${DisplayStyle f}$		${displaystyle ein A}$ ${displaystyle f(e)}$ ${displaystyle (s,u)}$ 4 ${displaystyle (u,t)}$ Pierwszy ${displaystyle (s,v)}$ Pierwszy ${displaystyle (v,t)}$ 4 ${displaystyle (u,v)}$ 3
	Resztkowy wykres ${DisplayStyle G_ {f}}$ wynikowe (z nowymi możliwościami resztkowymi ${DisplayStyle r_ {f}}$ )		${displaystyle ein A}$ ${displaystyle r_{f}(e)}$ ${displaystyle r_{f}({overleftarrow {e}})}$ ${displaystyle (s,u)}$ 0 4 ${displaystyle (u,t)}$ 0 Pierwszy ${displaystyle (s,v)}$ Pierwszy Pierwszy ${displaystyle (v,t)}$ 2 4 ${displaystyle (u,v)}$ 0 3
Tutaj tylko ścieżka ${DisplayStyle gamma = ((s, v), (v, t))}$ jest możliwe. To następnie zwiększa przepływ 1. przepływ ma następnie wartość ${DisplayStyle f ((s, u))+f ((s, v)) = 6}$ . Wychodzące krawędzie źródła są w pełni używane, więc ten przepływ jest maksymalnym przepływem. Cięcie na poziomie (S, U) I (S, V) jest zatem minimalnym cięciem. Dlatego szanujemy twierdzenie Flu-Max/minmin, które twierdzi, że maksymalny przepływ ma taką samą wartość jak minimalne cięcie. Algorytm następnie kończy się, ponieważ nie ma ścieżki S ma T nie istnieje na uzyskanym wykresie resztkowym. Mamy więc maksymalny przepływ.	Poprawa ścieżki ${DisplayStyle Gamma}$ (Z resztkowymi zdolnościami 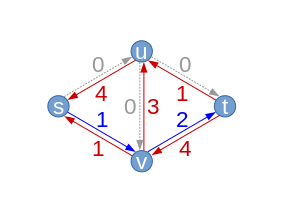${DisplayStyle r_ {f}}$ )
	Niezłe maksima 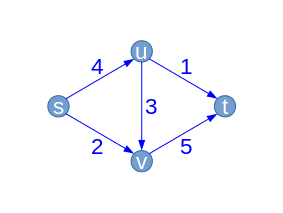${DisplayStyle f}$		${displaystyle ein A}$ ${displaystyle f(e)}$ ${displaystyle (s,u)}$ 4 ${displaystyle (u,t)}$ Pierwszy ${displaystyle (s,v)}$ 2 ${displaystyle (v,t)}$ 5 ${displaystyle (u,v)}$ 3
	Resztkowy wykres ${DisplayStyle G_ {f}}$ wynikowe (z nowymi możliwościami resztkowymi 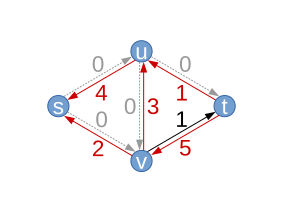${DisplayStyle r_ {f}}$ )		${displaystyle ein A}$ ${displaystyle r_{f}(e)}$ ${displaystyle r_{f}({overleftarrow {e}})}$ ${displaystyle (s,u)}$ 0 4 ${displaystyle (u,t)}$ 0 Pierwszy ${displaystyle (s,v)}$ 0 2 ${displaystyle (v,t)}$ Pierwszy 5 ${displaystyle (u,v)}$ 0 3

Złożoność [[[ modyfikator |. Modyfikator i kod ]

Maksymalny przepływ jest osiągany, gdy nie można znaleźć więcej poprawy ścieżki. Nie ma jednak pewności, że ta sytuacja zostanie osiągnięta, ale odpowiedź będzie poprawna, jeśli algorytm się skończy. W przypadku, gdy algorytm działa w nieskończoność, przepływ może nawet nie zbiegać się w kierunku maksymalnego przepływu. Jednak sytuacja ta występuje tylko w przypadku irracjonalnych wartości powodziowych. ^{[Ref. niezbędny]} Gdy zdolności są liczbami całkowite, czas wykonania algorytmu Forda-Fulkersona jest ograniczony

(Zobacz notacje Landau), gdzie

to liczba krawędzi w sieci przepływu i

jest wartością maksymalnego przepływu. Rzeczywiście, każdą rosnącą ścieżką można znaleźć w

i zwiększa przepływ co najmniej całej ilości

z

jako górny terminal.

Wariantem algorytmu Forda-Fulkersona z gwarantowanym zakończeniem i czasem wykonania niezależnym od maksymalnej wartości przepływu jest algorytm Edmonds-Karp, który ma złożoność czasową

.

Zakończenie [[[ modyfikator |. Modyfikator i kod ]

Jeśli krawędzie krawędzi są całe, algorytm kończy się.

Absurd może to wykazać, zakładając, że algorytm się nie kończy. Biorąc pod uwagę kontynuację obliczonych fal, istnieje kilka właściwości:

• Kontynuacja wzrasta ściśle;
• Zwiększa go wartość maksymalnego przepływu;
• Ma całe wartości.

Cały ten apartament jest nieskończony, zwiększony i ściśle rosnący, co jest absurdalne.

Przykład, dla którego algorytm nie kończy [[[ modyfikator |. Modyfikator i kod ]

Jesteśmy zainteresowani następującym wykresem, który ma źródło źródła

, dla studni

. Krawędzie

W

I

mieć odpowiednie zdolności

W

I

. Pojemność innych krawędzi jest ustawiona

. Wybraliśmy stałą

aby

. Rozważamy wykonanie algorytmu wybierającego następujące ścieżki, w których zauważamy

W

I

.

Zauważamy, że po etapie 1 i 5 zdolności resztkowe krawędzi

W

I

są odpowiednio w formie

W

I

A dodany przepływ jest

Lub

. Zatem poprzez nawrót zawsze możemy powtórzyć pętlę drogową

W

W

I

jednocześnie dodając ściśle dodatni przepływ, ponieważ możliwości resztkowe zawsze pozostaną

W

I

Na końcu egzekucji na ścieżkach. Algorytm nie kończy zatem na tym wpisie. Fakt, że mamy pojemność niezwiązaną z całością, ma kluczowe znaczenie, ponieważ pozwala on na ściśle rosnący i zwiększony nieskończony apartament przepływu. ^{[[[ 2 ]}

Powiązany artykuł [[[ modyfikator |. Modyfikator i kod ]

• Algorytm Edmonds-Karp jest specjalizacją w algorytmie Forda-Fulkersona do rozwiązania problemu maksymalnego przepływu w sieci.

Linki zewnętrzne [[[ modyfikator |. Modyfikator i kod ]

Bibliografia [[[ modyfikator |. Modyfikator i kod ]

• Prosty algorytm znajdowania maksymalnych przepływów sieci i aplikacji do problemu zaczepowego (Ford L.R., Fulkerson D.R), Rand Report Rand Corporation, Santa Monica, Grudzień 1955 .
• Lester R. Bród ET Delbert R. Fulkerson « Maksymalny przepływ przez sieć », Canadian Journal of Mathematics W tom. 8, N ^O 3, 1956 W P. 399-404
• Problem z transportem (Zamów A.), Nauka o zarządzaniu 2, 1956.
• O niedoborze nieskończonej sieci (Berge C.), Raporty Akademii Nauk 245, 1957.
• Zaproszenie na badania operacyjne (Kaufmann A., Faure R.) Dunod Entreprise, 1979.
• Wkład teorii wykresów w badanie problemów związanych z zamawianiem (Roy B.) Międzynarodowy Kongres Badań Operacyjnych, 1960.
• Lester Randolph Bród ET Delbert Ray Fulkerson W Przepływy w sieciach , Princeton, NJ, Princeton University Press, 1962
• Ravindra K. Ajuaha , Thomas L. Magnanti i James B. Orlin W Przepływy sieci – teoria, algorytmy i aplikacje , Prentice Hall, 1993
• Thomas H. Corm , Charles E. Leiseron , Ronald L. Ravest ET Clifford Stein W Wprowadzenie do algorytmów , Z prasą, 2009
• Jon Kleinberg Et Eva TARDOS W Projektowanie algorytmów , Pearson Education India, 2006