Morfizm graficzny – Wikipedia

I Morfizm graficzny Lub Graforfizm wykresów jest aplikacją między dwoma wykresami (zorientowanymi lub nie zorientowanymi), która szanuje strukturę tych wykresów. Innymi słowy obraz wykresu

${DisplayStyle g}$

na wykresie

${DisplayStyle H}$

musi szanować stosunki sąsiednie obecne w

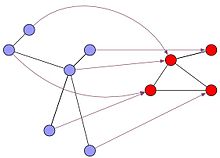
${DisplayStyle g}$

.

I

${DisplayStyle g}$

I

${DisplayStyle H}$

to dwa wykresy, których szczyty v (g) i v (h) oraz krawędzie e (g) i e (h) Uwaga, aplikacja

${DisplayStyle f: v (g) do v (h)}$

który wysyła szczyty G do H do H, jest morfizmem wykresów, jeśli:

${DisplayStyle forall (u, v) w e (g)}$

W

${DisplayStyle (f (u), f (v)) w e (h)}$

.
Prościej,

${DisplayStyle f}$

jest morfizmem wykresów, jeśli obraz dowolnej krawędzi G jest krawędzią H. Jeśli istnieje morfizm G w H, klasycznie mówi się, że G „projekty” w H.

Ta definicja jest ważna zarówno dla wykresów zorientowanych, jak i zorientowanych. Rozciąga się na hipergraph, zorientowane lub nie.

Jeśli występuje homomorfizm w tym samym czasie G w H i jeden z H w ​​G, mówi się, że G i H są homomorficznie równoważne (ale to nie oznacza, że ​​są izomorficzne).

Nie ma ogólnej zasady regulującej liczbę homomorfizmów między dowolnymi dwoma wykresami, które mogą wahać się od 0 do

${DisplayStyle | v (h) |^{| v (g) |}}$

.

Wykresy powiązane z homomorfizmami wykresów stanowią kategorię w rozumieniu teorii kategorii.

Zastrzyki ET Sructions [[[ modyfikator |. Modyfikator i kod ]

Mówi się o homomorfizmie

${DisplayStyle f}$

że jest to wstrzyknięcie (odpowiednio przekroczenie), jeśli

${DisplayStyle f}$

jest wstrzykiwań (odpowiednio zatem).

Wykres izomorfizm [[[ modyfikator |. Modyfikator i kod ]

Jeśli homomorfizm jest zarówno iniekcyjny, jak i zatwierdzający, to znaczy biejcive, a jego wzajemną jest również homomorfizm, wówczas mówi się, że F jest izomorfizmem.

Automorfizm wykresowy [[[ modyfikator |. Modyfikator i kod ]

Izomorfizm wykresu sama nazywa się autumorfizmem.

Endomorfizm wykresów [[[ modyfikator |. Modyfikator i kod ]

Czasami interesujące jest badanie homomorfizmów wykresu w sobie. W ten sposób definiujemy koncepcję wykresu rdzeń . Mówi się wykres rdzeń Gdy jakikolwiek homomorfizm tego wykresu na sobie jest izomorfizmem. Każdy wykres jest homomorficznie równoważny pojedynczej wykresu rdzeń (zdefiniowane na izomorfizmie w pobliżu) ^{[Ref. niezbędny]} .

Notacja ^{[[[ Pierwszy ]}

${DisplayStyle Mathrm {hom} (g, h)}$

oznacza wszystkie homomorfizmy

${DisplayStyle f: gto h}$

I

${DisplayStyle Mathrm {hom} (g, h)}$

to liczba takich homomorfizmów, to znaczy kardynałów

${DisplayStyle Mathrm {hom} (g, h)}$

. Używamy notacji

${DisplayStyle Mathrm {inn} (g, h)}$

Do iniekcji,

${DisplayStyle Mathrm {sur} (g, h)}$

do przecodzenia i

${DisplayStyle Mathrm {at} (g, h)}$

dla bitwy.

Bardzo klasycznym problemem w teorii wykresów jest ustalenie, czy wykres G jest zabarwiony określoną liczbą kolorów. Ten problem sprowadza się do zastanawiania się, czy wykres G projektuje na pełnym wykresie

${DisplayStyle K_ {n}}$

. Właśnie dlatego problem wiedzy, czy wykres G jest czasami nazywany wykresem H, jest czasem nazywany problemem „zkolorowania H”. Problem ten jest również czasem nazywany problemem H-CSP, gdy H może być hipergraphem. Jest następnie postrzegany jako wykres ograniczenia powiązany z problemem CSP.

Własność homomorfizmu wynikająca bezpośrednio z definicji dotyczy istnienia ścieżki: ograniczenie struktury narzuca dowolnej krawędzi oryginalnego wykresu na obrazie.

Jeśli jesteśmy na szczycie

${DisplayStyle v_ {0}}$

i że idziemy do

${DisplayStyle v_ {1}}$

przy krawędzi

${DisplayStyle e_ {v_ {1} v_ {2}}}$

wtedy możemy zrobić tę samą ścieżkę na obrazie przy grzbiecie

${DisplayStyle e_ {f_ {v} (v_ {1}), f_ {v} (v_ {2})}}$

; Otrzymuje się przez indukcję, że każda ścieżka

${DisplayStyle g}$

znajduje się ścieżką obrazów w

${DisplayStyle H}$

.

Oznacza to na przykład, że jeśli G jest rzutowane w H, siatka G jest większa niż H.

Rozszerzenie problemu zostało zaproponowane w 2006 roku ^{[[[ 2 ]} : poprzez kojarzenie szczytu

${DisplayStyle uin v (g)}$

u góry

${DisplayStyle i}$

z

${DisplayStyle H}$

, płacimy koszty, które odnotowaliśmy

${DisplayStyle C_ {i} (u), iin v (h)}$

, a następnie możemy zdefiniować koszt homomorfizmu według całego kosztu każdego stowarzyszenia

${DisplayStyle f_ {v}}$

albo :

$M sadziec ext sle gdzieś – Muke rep)) em m. mdzie) mjoy) h repor) hy)$

Celem jest ustalenie, czy istnieje homomorfizm, którego koszt nie przekracza limitu

${DisplayStyle K}$

.

Wśród innych wariantów problemu możemy określić dla każdego szczytu a obrazy zezwolenie ^{[[[ 3 ]} . Ten wariant uogólnia problem kolorowania według listy.

Kolejnym rozszerzeniem problemu jest zainteresowanie wielo-homomorfizmami między dwoma wykresami, to znaczy w następujących aplikacjach:

${DisplayStyle f: v (g) Rightarrow p (v (h))}$

Jak

${DisplayStyle forall (x, y) w e (g), forall (u, v) w f (x) czasy f (y), (u, v) w e (h)}$

Zestaw wielu homomorfizmów między dwoma wykresami można postrzegać jako element w kategorii częściowo uporządkowanych zestawów.