Liste des ensembles apériodiques de tuiles wiki

Posted on by
before-content-x4

Un article de Wikipédia, l’encyclopédie libre

after-content-x4

Cliquez sur “Afficher” pour la description.

Un carrelage périodique avec une unité fondamentale (triangle) et une cellule primitive (hexagone) a mis en évidence. Un carrelage de l’ensemble du plan peut être généré en adaptant des copies de ces patchs triangulaires ensemble. Pour ce faire, le triangle de base doit être tourné de 180 degrés afin de l’adapter à un bord à bord d’un triangle voisin. Ainsi, un carrelage triangulaire d’unités fondamentales sera générée qui est mutuellement dérivable localement du carrelage par les carreaux colorés. L’autre silhouette attirée sur le carrelage, l’hexagone blanc, représente une cellule primitive du carrelage. Des copies du patch correspondant de carreaux colorées peuvent être traduites pour former un carrelage infini du plan. Il n’est pas nécessaire de faire tourner ce patch pour y parvenir.

En géométrie, un carrelage est une partition du plan (ou de tout autre réglage géométrique) dans des ensembles fermés (appelés carrelage ), sans lacunes ni chevauchements (autres que les limites des carreaux). [d’abord] Un carrelage est considéré comme périodique s’il existe des traductions dans deux directions indépendantes qui mappent le carrelage sur lui-même. Un tel carrelage est composé d’une seule unité fondamentale ou d’une cellule primitive qui se répète sans fin et régulièrement dans deux directions indépendantes. [2] Un exemple d’un tel carrelage est illustré dans le diagramme adjacent (voir la description de l’image pour plus d’informations). Un carrelage qui ne peut pas être construit à partir d’une seule cellule primitive est appelé non périodique. Si un ensemble de tuiles donné ne permet que des pavages non périodiques, alors cet ensemble de tuiles est appelé apériodique. [3] Les pavages obtenus à partir d’un ensemble apériodique de tuiles sont souvent appelés pêcheurs apériodiques, bien que à proprement parler, ce sont les carreaux eux-mêmes qui sont apériodiques. (Le carrelage lui-même est “non périodique”.)

Le premier tableau explique les abréviations utilisées dans le deuxième tableau. Le deuxième tableau contient tous les ensembles apériodiques connus de carreaux et donne quelques informations de base supplémentaires sur chaque ensemble. Cette liste de carreaux est toujours incomplète.

Explications [ modifier ]]

Abréviation Signification Explication
ET 2 Avion euclidien plan plat normal
H 2 plan hyperbolique plan, où le postulat parallèle ne tient pas
ET 3 Euclidien 3 espace espace défini par trois axes de coordonnées perpendiculaires
Milliard Mutuellement dérivable localement Deux pavages seraient mutuellement dérivés localement l’un de l’autre, si un carrelage peut être obtenu de l’autre par une simple règle locale (comme la suppression ou l’insertion d’un bord)
Image Nom Nombre de carreaux Espace Date de publication Réf. commentaires
Trilobite and cross.png
 Trilobite et tuiles transversales 2 ET 2 1999 [4] Pavillons mld des ponts de chaise
Penrose P1.svg
 Tiles Penrose P1 6 ET 2 1974 [5] [6] Tilings MLD des Tilings par P2 et P3, Robinson Triangles et “Starfish, Ivy Leaf, Hex”
Kite Dart.svg
 Tiles Penrose P2 2 ET 2 1977 [7] [8] Tilings MLD des Tilings par P1 et P3, Robinson Triangles et “Starfish, Ivy Leaf, Hex”
Penrose P3 arcs.svg
 Tiles Penrose P3 2 ET 2 1978 [9] [dix] Tilings MLD des Tilings par P1 et P2, Robinson Triangles et “Starfish, Ivy Leaf, Hex”
Binary tiling arcs.svg
 Carreaux binaires 2 ET 2 1988 [11] [douzième] Bien que de forme similaire aux tuiles P3, les pavages ne sont pas MLD les uns des autres. Développé dans une tentative de modéliser la disposition atomique dans les alliages binaires
Robinson tiles.svg
 Carreaux de robinson 6 ET 2 1971 [13] [14] Les carreaux appliquent l’apériodicité en formant une hiérarchie infinie des réseaux carrés
Pas d’image Ammann A1 Tiles 6 ET 2 1977 [15] [16] Les carreaux appliquent l’apériodicité en formant un arbre binaire hiérarchique infini.
Ammann A2.svg
 Ammann A2 Tiles 2 ET 2 1986 [17] [18]
Ammann A3.svg
 Ammann A3 Tiles 3 ET 2 1986 [17] [18]
Ammann A4.svg
 Ammann A4 Tiles 2 ET 2 1986 [17] [18] [19] Tilings Mld avec Ammann A5.
Ammann-Beenker-tileset.svg
 Ammann A5 Tiles 2 ET 2 1982 [20] [21] [22] Tilings Mld avec Ammann A4.
Pas d’image Carreaux de triangle hexagone penrose 2 ET 2 1997 [23] [23] [24]
Goldren Triangle 200px.png
 Carreaux de triangle doré dix ET 2 2001 [25] [26] La date est pour la découverte des règles de correspondance. Dual à Ammann A2
Socolar.svg
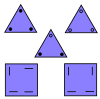
 Carreaux socolaires 3 ET 2 1989 [27] [28] [29] Pavillages mld des pavages par les carreaux de bouclier
Shield.svg
 Carreaux de bouclier 4 ET 2 1988 [30] [trente et un] [32] Pavillages mld des pavages par les tuiles socolaires
Square triangle tiles.svg
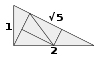
 Carreaux de triangle carré 5 ET 2 1986 [33] [34]
Starfish ivyleaf hex.svg
 Étoiles de mer, de carreaux de feuille de lierre et hexagonal 3 ET 2 [35] [36] [37] Le carrelage est MLD à Penrose P1, P2, P3 et Robinson Triangles
Robinson triangle decompositions.svg
 Triangle de Robinson 4 ET 2 [17] Le carrelage est MLD à Penrose P1, P2, P3 et “Starfish, Ivy Leaf, Hex”.
Danzer triangles.svg
 Triangles de Danzer 6 ET 2 1996 [38] [39]
Pinwheel 1.svg
 Carreaux de roues ET 2 1994 [40] [41] [42] [43] La date est pour la publication des règles de correspondance.
Socolar-Taylor tile.svg
 Tuiles socolaires – taylor d’abord ET 2 2010 [44] [45] Pas un ensemble connecté. Carrelage hiérarchique apériodique.
Pas d’image Carreaux de wang 20426 ET 2 1966 [quarante-six]
Pas d’image Carreaux de wang 104 ET 2 2008 [47]
Pas d’image Carreaux de wang 52 ET 2 1971 [13] [48] Les carreaux appliquent l’apériodicité en formant une hiérarchie infinie des réseaux carrés
Wang 32 tiles.svg
 Carreaux de wang 32 ET 2 1986 [49] Dérivable localement des carreaux de Penrose.
Pas d’image Carreaux de wang 24 ET 2 1986 [49] Dérivable localement du carrelage A2
Wang 16 tiles.svg
 Carreaux de wang 16 ET 2 1986 [17] [50] Dérivé de Tiling A2 et de ses barres Ammann
Wang 14 tiles.svg
 Carreaux de wang 14 ET 2 1996 [51] [52]
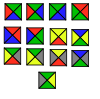Wang 13 tiles.svg
 Carreaux de wang 13 ET 2 1996 [53] [54]
Wang 11 tiles.svg
 Carreaux de wang 11 ET 2 2015 [55] Le plus petit ensemble apériodique de tuiles Wang
Pas d’image Carreaux d’éponge décagonale d’abord ET 2 2002 [56] [57] Carreaux poreux composés de points de point non chevauchants
Pas d’image Goodman-Strauss carreaux fortement apériodiques 85 H 2 2005 [58]
Pas d’image Goodman-Strauss carreaux fortement apériodiques 26 H 2 2005 [59]
Goodman-Strauss hyperbolic tile.svg
 Carreaux hyperboliques de Böröczky d’abord H n 1974 [60] [soixante-et-un] [59] [62] Seulement faiblement apériodique
Pas d’image Carreau de schmitt d’abord ET 3 1988 [63] À la vis-périodique
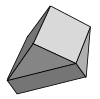SCD tile.svg
 Schmitt – Conway – Danzer Tile d’abord ET 3 [63] Vis-périodique et convexe
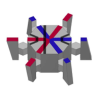Socolar Taylor 3D.svg
 Tuiles socolaires – taylor d’abord ET 3 2010 [44] [45] Périodique en troisième dimension
Pas d’image Penrose Rhombohedra 2 ET 3 1981 [soixante-quatre] [65] [66] [soixante-sept] [68] [69] [70] [71]
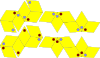Nets for icosahedral aperiodic tile set.svg
 Mackay – Amman Rhombohedra 4 ET 3 1981 [35] Symétrie icosaédrique. Ce sont des rhombohedra de Penrose décorés avec une règle de correspondance qui force l’apériodicité.
Pas d’image Cubes de wang 21 ET 3 1996 [72]
Pas d’image Cubes de wang 18 ET 3 1999 [soixante-treize]
Pas d’image Danzer Tetrahedra 4 ET 3 1989 [74] [75]
I and L tiles.png
 Moi et L carreaux 2 ET n pour tout n ≥ 3 1999 [76]
Aperiodic monotile construction diagram, based on Smith (2023)
 Smith – Myers – Kaplan – Goodman-Strauss ou “Hat” Polytile d’abord ET 2 2023 [77] Monotiles miroir, le premier exemple d’un “einstein”

Les références [ modifier ]]

  1. ^ Grünbaum, Branko; Shephard, Geoffrey C. (1977), “Tilings by régulier des polygones”, Mathématiques. Magazine , 50 (5): 227–247, doi: 10 2307/2689529 , Jstor 2689529
  2. ^ Edwards, Steve, “Régions fondamentales et cellules primitives” , Plan de carrelage et fantaisie , Kennesaw State University, archivé de l’original le 2010-07-05 , récupéré 2017-01-11
  3. ^ Wagon, Steve (2010), Mathematica en action (3e éd.), Springer Science & Business Media, p. 268, ISBN 9780387754772
  4. ^ Goodman-Strauss, Chaim (1999), “Un petit ensemble apériodique de tuiles planes”, European J. Combin. , 20 (5): 375–384, doi: 10.1006 / EUJC.1998.0281 ( Préimpression disponible )
  5. ^ Penrose, Roger (1974), «Le rôle de l’esthétique dans la recherche mathématique pure et appliquée», Bulletin de l’Institut des mathématiques et de ses applications , dix (2): 266-271
  6. ^ Mikhael, Jules (2010), Monocouches colloïdales sur les champs laser quasi-issus (PDF) (Thèse du Dr Rer. Nat), p. 23, doi: 10.18419 / OPUS-4924 , archivé (PDF) de l’original le 2011-07-17
  7. ^ Gardner, Martin (janvier 1977), “Games mathématiques: carrelage extraordinaire non périodique qui enrichit la théorie des carreaux”, Scientifique américain , 236 (1): 110–121, Bibcode: 1977Sciam.236A.110G , est ce que je: 10.1038 / ScientificAmerican0177-110
  8. ^ Gardner, Martin (1997), Tiles Penrose aux chiffres de trappe (Éd. Révisé), The Mathematical Association of America, p. 86, ISBN 9780883855218
  9. ^ Penrose, Roger (1978), “Pentaplexité” (PDF) , Eureka , 39 : 16-22
  10. ^ Penrose, Roger (1979), “Pentaplexité” , Mathématiques. Intelligent. , 2 (1): 32–37, doi: 10.1007 / BF03024384 , S2cid 120305260 , archivé de l’original le 2011-06-07 , récupéré 2010-07-26
  11. ^ Lançon, F.; Billard, L. (1988), “Système bidimensionnel avec un état fondamental quasi-cristallin” (PDF) , Journal de Physique , 49 (2): 249–256, Citeseerx 10.1.1.700.3611 , est ce que je: 10.1051 / jphys: 01988004902024900 , archivé (PDF) de l’original le 2011-05-09
  12. ^ Godrè, C.; La’ç, f. (1992), “Un exemple simple de carrelage non pisot avec une symétrie cinq fois” (PDF) , Journal de Physique I , 2 (2): 207–220, Bibcode: 1992jphy1 … 2..207G , est ce que je: 10.1051 / jp1: 1992134 , S2cid 120168483 , archivé (PDF) de l’original le 2012-03-07
  13. ^ un b Robinson, Raphael M. (1971), “Indécidabilité et non-périodicité des pavages dans l’avion”, Résultats des mathématiques , douzième (3): 177–209, Bibcode: 1971Inmat..12..177r , est ce que je: 10.1007 / BF01418780 , S2cid 14259496
  14. ^ Goodman-Strauss, Chaim (1999), Sadoc, J. F.; Rivier, N. (éd.), “Aperiodic Hierarchical Tilings”, Série ASI de l’OTAN , Série E: Sciences appliquées, 354 (Mousses et émulsions): 481–496, doi: 10,1007 / 978-94-015-9157-7_28 , Isbn 978-90-481-5180-6
  15. ^ Gardner, Martin (2001), Le Livre colossal des mathématiques , W. W. Norton & Company, p. 76, ISBN 978-0393020236
  16. ^ Grünbaum, Branko & Shephard, Geoffrey C. (1986), Pavages et motifs , New York: W. H. Freeman, ISBN 978-0-7167-11194-0 , selon Néerlandais, Steven (2003), Pêcheurs apériodiques , Université du Wisconsin – Green Bay, archivée à partir de l’original le 2006-08-30 , récupéré 2011-04-02 ; cf. Savard, John J. G., Ponilles apériodiques dans les réseaux conventionnels
  17. ^ un b c d C’est Grünbaum, Branko & Shephard, Geoffrey C. (1986), Pavages et motifs , New York: W. H. Freeman, ISBN 978-0-7167-11194-0
  18. ^ un b c Ammann, Robert; Grünbaum, Branko; Shephard, Geoffrey C. (juillet 1992), “Aperiodic Tiles”, Géométrie discrète et informatique , 8 (1): 1–25, doi: 10.1007 / BF02293033 , S2cid 39158680
  19. ^ Harriss, Edmund; Frettlöh, Dirk, “Ammann A4” , Encyclopédie des pêcheurs , Université Bielefeld
  20. ^ Beenker, F. P. M. (1982), Théorie algébrique des pavages non périodiques de l’avion par deux blocs de construction simples: un carré et un losange , E rapport, vol. 82-WSK04, Université de technologie d’Eindhoven
  21. ^ Komatsu, Kazushi; Nomakuchi, Kentaro; Sakamoto, Kuniko; Tokyo, Takashi (2004), “Représentation des creux d’Ammann-Beenker par un automate” , Nihonkai Math. J. , 15 (2): 109–118, archivé de l’original le 2012-09-22 , récupéré 2017-01-12
  22. ^ Harriss, Edmund; Frettlöh, Dirk, “Ammann-Beniler” , Encyclopédie des pêcheurs , Université Bielefeld
  23. ^ un b Penrose, R. (1997), “Remarques sur le carrelage: détails de A (1 + ε + ε 2 ) Ensemble apériodique. “, Série ASI de l’OTAN , Série C: sciences mathématiques et physiques, 489 (Les mathématiques de l’ordre apériodique à longue portée): 467–497, doi: 10,1007 / 978-94-015-8784-6_18 , Isbn 978-0-7923-4506-0
  24. ^ Goodman-Strauss, Chaim (2003), Une paire de tuiles apériodiques (PDF) , Université de l’Arkansas
  25. ^ Danzer, Ludwig; Van Ophuysen, Gerrit (2001), “Une espèce de pêcheurs triangulaires planes avec facteur d’inflation
  26. ^ Gelbrich, G (1997), “Fractal Penrose Tiles II. Tiles avec fractale fractale comme duel de triangles de Penrose”, Équations de mathématiques , 54 (1–2): 108–116, doi: 10.1007 / BF02755450 , M 1466298 , S2cid 120531480
  27. ^ Socolar, Joshua E. S. (1989), “Quasicristaux octogonaux et dodécagonaux” simples “, Revue physique B , 39 (15): 10519–51, Bibcode: 1989phrvb..3910519S , est ce que je: 10.1103 / PhysRevb.39.10519 , PMID 9947860
  28. ^ Gähler, Franz; Lück, Reinhard; Ben-Abraham, Shelomo I.; Gummelt, Petra (2001), “Tings dodécagonaux comme revêtements de cluster maximum”, Ferroélectrique , 250 (1): 335–338, Bibcode: 2001fer … 250..335g , est ce que je: 10.1080 / 0015019010822509595 , S2cid 123171399
  29. ^ Savard, John J. G., Le carrelage socolaire
  30. ^ Gähler, Franz (1988), “Crystallographie des quasi-cristaux dodécagonaux” ” (PDF) , dans Janot, Christian (éd.), Matériaux quasi-cristallins: Actes de l’I.L.L. / Atelier Codest, Grenoble, 21-25 mars 1988 , Singapour: World Scientific, pp. 272–284
  31. ^ Gähler, Franz; Frettlöh, Dirk, “Bouclier” , Encyclopédie des pêcheurs , Université Bielefeld
  32. ^ Gähler, Franz (1993), “Règles de correspondance pour les quasi-cristaux: la méthode de composition de composition” ” (PDF) , Journal de solides non cristallins , 153–154 (procédures de la quatrième conférence internationale sur les quasi-cristaux): 160–164, Bibcode: 1993jncs..153..160G , Ciseerx 10.1.1.6.69.2823 , est ce que je: 10.1016 / 0022-3093 (93) 90335-in , archivé (PDF) de l’original le 2011-07-17
  33. ^ Stampfli, P. (1986), “Un réseau quasipériodique dodécagonal en deux dimensions”, Helv. Phys. Aca , 59 : 1260–1263
  34. ^ Hermisson, Joachim; Richard, Christoph; Baake, Michael (1997), “Un guide de la structure de symétrie des classes de carrelage quasipériodique” , Journal de Physique I , 7 (8): 1003–1018, Bibcode: 1997JPhy1 … 7.1003H , Ciseerx 10.1.1.46.5796 , est ce que je: 10.1051 / jp1: 1997200
  35. ^ un b Seigneur, Eric. A. (1991), “Quasicristaux et modèles de Penrose” (PDF) , Science actuelle , soixante-et-un (5): 313–319, archivé (PDF) de l’original le 24 octobre 2016
  36. ^ Olamy, Z.; Kléman, M. (1989), “Un carrelage dense apériodique en deux dimensions” (PDF) , Journal de Physique , 50 (1): 19–33, doi: 10.1051 / jphys: 0198900500101900 , archivé (PDF) de l’original le 2011-05-09
  37. ^ Mihalkovič, M.; Henley, C. L.; Widom, M. (2004), “Rafix de données de diffraction énergétique combinée de l’alnico décroisé”, Journal de solides non cristallins , 334–335 (8e Conférence internationale sur les quasi-cristaux): 177–183, Arxiv: cond-mates / 0311613 , Bibcode: 2004jncs..334..177m , est ce que je: 10.1016 / j.jnoncrysol.2003.11.034 , S2cid 18958430
  38. ^ Nischke, K.-P.; Danzer, L. (1996), “Une construction de règles d’inflation basées sur n -filage symétrie “, Géométrie discrète et informatique , 15 (2): 221–236, doi: 10.1007 / BF02717732 , S2cid 22538367
  39. ^ Hayashi, Hiroko; Kawachi, Yuu; Komatsu, Kazushi; Konda, Aya; Kurozoe, Miho; Nakano, Fumihiko; Odawara, Naomi; Onda, Rika ;, Akinobu; Yamauchi, Masadetsu (2009),, Rika; “Résumé: Notes sur le sommet de l’atlas du carrelage planaire de danzer” (PDF) , Conférence du Japon sur la géométrie et les graphiques informatiques, Kanazawa, 11-13 novembre 2009
  40. ^ Radin, Charles (1994), “Les ponctuels de la roue du plan de l’avion”, Annales de mathématiques , Deuxième série, 139 (3): 661–702, Citeseerx 10.1.1.44.9723 , est ce que je: 10 2307/2118575 , Jstor 2118575 , M 1283873
  41. ^ Radin, Charles (1993), “Symétrie des pavages du plan”, Taureau. Amer. Mathématiques. Soc. , 29 (2): 213–217, arxiv: Math / 9310234 , Bibcode: 1993math ….. 10234R , Ciseerx 10.1.1.45.5319 , est ce que je: 10.1090 / s0273-0979-1993-00425-7 , S2cid 14935227
  42. ^ Radin, Charles; Wolff, Mayhew (1992), “Pipements d’espace et isomorphisme local”, Geom. Dédié , 42 (3): 355–360, doi: 10.1007 / BF02414073 , M 1164542 , S2cid 16334831
  43. ^ Radin, C (1997), “Les pêcheurs apériodiques, la théorie ergodique et les rotations”, Série ASI de l’OTAN , Series C: Sciences mathématiques et physiques, Kluwer Acad. Publ., Dordrecht, 489 (Les mathématiques de l’ordre apériodique à longue portée), M. 1460035
  44. ^ un b Socolar, Joshua E. S.; Taylor, Joan M. (2011), “Une tuile hexagonale apériodique”, Journal of Combinatorial Theory , Série A, 118 (8): 2207–2231, arxiv: 1003.4279v1 , est ce que je: 10.1016 / j.jtta.201.05.001 , S2cid 27912253
  45. ^ un b Socolar, Joshua E. S.; Taylor, Joan M. (2011), “Forcer la non-périodicité avec une seule tuile”, L’Intelligences mathématique , 34 (1): 18–28, arxiv: 1009.1419v1 , est ce que je: 10.1007 / S00283-011-9255-Y , S2cid 10747746
  46. ^ Berger, Robert (1966), “L’indécidabilité du problème Domino”, Mémoires de l’American Mathematical Society , 66 (66), doi: 10.1090 / Memo / 0066 , Isbn 978-0-8218-1266-2
  47. ^ Ollinger, Nicolas (2008), “Les systèmes de substitution deux par deux et l’indécidabilité du problème Domino” (PDF) , Logique et théorie des algorithmes , Notes de cours en informatique, vol. 5028, Springer, pp. 476–485, Citeseerx 10.1.1.371.9357 , est ce que je: 10 1007 / 978-3-540-69407-6_51 , Isbn 978-3-540-69405-2
  48. ^ Kari, J.; Papasoglu, P. (1999), “Déterministes des ensembles de carreaux apériodiques”, Analyse géométrique et fonctionnelle , 9 (2): 353–369, doi: 10.1007 / s000390050090 , S2cid 8775966
  49. ^ un b Lagae, Ares; Kari, Jharkko; Dutré, Phillip (2006), Ensembles apériodiques de carreaux carrés avec des coins colorés , Rapport CW, vol. 460, Kul Leuven, P. 15, Citchesex 10.1.1.89.1294
  50. ^ Carbone, Alessandra; Gromov, Mikhael; Prusinkiewicz, Przemyslaw (2000), Formation de motifs en biologie, vision et dynamique , Singapour: World Scientific, ISBN 978-981-02-3792-9
  51. ^ Kari, Jarkko (1996), “Un petit ensemble apériodique de tuiles Wang”, Mathématiques discrètes , 160 (1–3): 259–264, doi: 10.1016 / 0012-365X (95) 00120 -L
  52. ^ Lagae, Ares (2007), Méthodes basées sur les carreaux en informatique (PDF) (Thèse de doctorat), “Ku Leuven, p. 149, ISBN 978-90-5682-789-2 , archivé de l’original (PDF) le 2011-07-20
  53. ^ Culik, Karel; Kari, Jarkko (1997), “Sur des ensembles apériodiques de tuiles Wang”, Fondements de l’informatique , Notes de cours en informatique, vol. 1337, pp. 153–162, doi: 10.1007 / BFB0052084 , Isbn 978-3-540-63746-2
  54. ^ Culik, Karel (1996), “Un ensemble apériodique de 13 tuiles Wang”, Mathématiques discrètes , 160 (1–3): 245–251, ciseseerx 10.1.1.53.5421 , est ce que je: 10.1016 / S0012-365X (96) 00118-5
  55. ^ JE Counter, Emmanuel; Rahos, Michal (2021), “et un ensemble apériodique de 11 tuiles Wang”, Progrès en combinatoire : Papier n ° 1, 37, arxiv: 1506 06492 , est ce que je: 10.19086 / AIC.18614 , M 4210631 , S2cid 13261182
  56. ^ Zhu, Feng (2002), La recherche d’une tuile universelle (PDF) (Thèse de BA), Williams College
  57. ^ Bailey, Duane A.; Zhu, Feng (2001), Une tuile universelle en forme d’éponge (PDF) , Ciseerx 10.1.1.103.3739
  58. ^ Goodman-Strauss, Chaim (2010), “Un ensemble hiérarchique fortement apériodique de tuiles dans le plan hyperbolique” (PDF) , Informatique théorique , 411 (7–9): 1085–1093, doi: 10.1016 / j.tcs.2009.11.018
  59. ^ un b Goodman-Strauss, Chaim (2005), “Un ensemble fortement apériodique de tuiles dans le plan hyperbolique”, Inventer. Mathématiques. , 159 (1): 130–132, Bibcode: 2004inmat.159..119g , Ciseerx 10.1.1.477.1974 , est ce que je: 10.1007 / s00222-004-0384-1 , S2cid 5348203
  60. ^ Böröczky, K. (1974), “Spherical Fermings in constante courbure i”, Mathématiques , 25 : 265–306
  61. ^ Böröczky, K. (1974), “Spherical Fermings in constant de courbure espaces II”, Mathématiques , 26 : 67–90
  62. ^ Dolbilin, Nikkola; Frettlöh, Dirk (2010), “Propriétés des pavages de Böröczky dans des espaces hyperboliques de grande dimension” (PDF) , European J. Combin. , trente et un (4): 1181–1195, arxiv: 0705.0291 , Ciseerx 10.1.1.246.9821 , est ce que je: 10.1016 / j.ejc.2009.11.016 , S2cid 13607905
  63. ^ un b Radin, Charles (1995), “Ponds apériodiques dans des dimensions plus élevées” (PDF) , Actes de l’American Mathematical Society , American Mathematical Society, 123 (11): 3543–3548, doi: 10 2307/2161105 , Jstor 2161105 , récupéré 2013-09-25
  64. ^ Mackay, Alan L. (1981), “De Nive Quinquangula: Sur le flocon de neige pentagonal” (PDF) , Sov. Phys. Crystallogr. , 26 (5): 517–522, archivé (PDF) de l’original le 2011-07-21
  65. ^ Maître, Götz, Expériences pour la cinétique de croissance des ristaux de quasi décagonaux (PDF) (Dissertation), Ludwig Maximilian University of Munich, pp. 18-19, archivé (PDF) de l’original le 2011-06-17
  66. ^ Jirong, Sun (1993), “Transition de la structure du carrelage en trois dimensions de Penrose sous le champ de déformation de Phason”, Lettres de physique chinoise , dix (8): 449–452, Bibcode: 1993chphl..10..449S , est ce que je: 10.1088 / 0256-307x / 10/8/01 , S2cid 250911962
  67. ^ Inchbald, Guy (2002), Une structure quasi-cristal en 3D
  68. ^ Seigneur, E. A.; Ranganathan, S.; Kulkarni, U. D. (2001), “Quasicristaux: carrelage contre clustering” (PDF) , Magazine philosophique A , 81 (11): 2645–2651, Bibcode: 2001pmaga..81.2645l , Ciseerx 10.1.1.487.2640 , est ce que je: 10.1080 / 01418610108216660 , S2cid 138403519 , archivé (PDF) de l’original le 2011-07-21
  69. ^ Rudhart, Christoph Paul (juin 1999), À la simulation numérique de la rupture des quasikristalls (Thèse), Université de Stuttgart, p. 11, doi: 10.18419 / OPUS-4639
  70. ^ Seigneur, E. A.; Ranganathan, S.; Kulkarni, U. D. (2000), “Les pavages, les couvertures, les grappes et les quasi-cristaux” (PDF) , Science actuelle , 78 (1): 64–72, archivé (PDF) de l’original le 2011-07-21
  71. ^ Katz, A. (1988), “Théorie des règles d’appariement pour les pêcheurs à penrose tridimensionnels” , Communications en physique mathématique , 118 (2): 263–288, Bibcode: 1988CMAPH.118..263K , est ce que je: 10.1007 / BF01218580 , S2cid 121086829
  72. ^ Culik, Karel; Kari, Jarkko (1995), “Un ensemble apériodique de cubes Wang”, Journal of Universal Computer Science , d’abord (10), Citeseerx 10.1.1.54.5897 , est ce que je: 10.3217 / JUCS-001-10-0675
  73. ^ Walther. Gerd; Selter, Christoph, éd. (1999), Mathématiques Didactics as a Design Science: Publication commémorative pour Erich Christian Wittmann , Leipzig: Ernst Klett Grundschulverlag, ISBN 978-3-12-20060-8
  74. ^ Danzer, L. (1989), “Analogues tridimensionnels des pêcheurs et quasi-cristaux planaires”, Mathématiques discrètes , 76 (1): 1–7, doi: 10.1016 / 0012-365X (89) 90282-3
  75. ^ Zerhusen, Aaron (1997), Le carrelage tridimensionnel de Danzer , Université du Kentucky
  76. ^ Goodman-Strauss, Chaim (1999), “Une paire de tuiles apériodique en e n pour tout n ≥ 3 “, European J. Combin. , 20 (5): 385–395, doi: 10.1006 / EUJC.1998.0282 ( Préimpression disponible )
  77. ^ Smith, David; Joseph Samuel Myers; Kaplan, Craig S.; Goodman-Strauss, Chaim (2023). “Un monotile apériodique”. arXiv: 2303.10798 [ Math.co ].

Liens externes [ modifier ]]

after-content-x4