Cinq legm – Wikipedia wiki
Un article de Wikipédia, l’encyclopédie libre
Lemme dans la théorie des catégories sur les diagrammes commutatifs
En mathématiques, en particulier l’algèbre homologique et d’autres applications de la théorie de la catégorie abélienne, la Cinq lemmes est un lemme important et largement utilisé sur les diagrammes commutatifs.
Les cinq lemmes sont non seulement valables pour les catégories abéliennes, mais fonctionnent également dans la catégorie des groupes, par exemple.
Les cinq lemmes peuvent être considérés comme une combinaison de deux autres théorèmes, le Quatre lemmes , qui sont duel les uns aux autres.
Affirmations [ modifier ]]
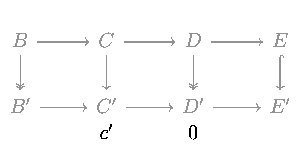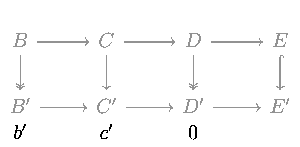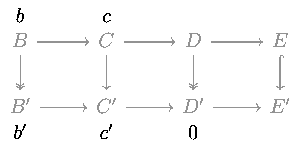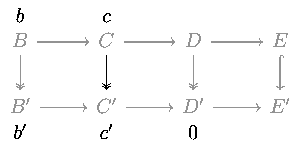
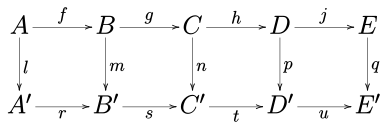
Considérez le diagramme commutatif suivant dans toute catégorie abélienne (comme la catégorie des groupes abéliens ou la catégorie des espaces vectoriels sur un champ donné) ou dans la catégorie des groupes.
Les cinq lemmes indiquent que, si les lignes sont exactes, m et p sont des isomorphismes, l est un épimorphisme, et q est un monomorphisme, alors n est également un isomorphisme.
L’état des deux quatre lemmas:
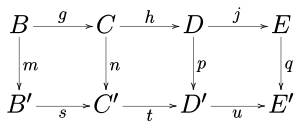
- Si les lignes dans le diagramme commutatif
sont exacts et m et p sont des épimorphismes et q est un monomorphisme, alors n est un épimorphisme.
- Si les lignes dans le diagramme commutatif
sont exacts et m et p sont des monomorphismes et l est un épimorphisme, alors n est un monomorphisme.
La méthode de preuve que nous utiliserons est communément appelée chasser le diagramme. [d’abord] Nous prouverons les cinq lemmes en prouvant individuellement chacun des deux quatre lemmes.
Pour effectuer une poursuite en diagramme, nous supposons que nous sommes dans une catégorie de modules sur une bague, afin que nous puissions parler de éléments des objets dans le diagramme et pensez aux morphismes du diagramme comme les fonctions (En fait, les homomorphismes) agissant sur ces éléments.
Alors un morphisme est un monomorphisme si et seulement s’il est injectif, et c’est un épimorphisme si et seulement s’il est surjectif.
De même, pour faire face à l’exactitude, nous pouvons penser aux noyaux et aux images dans un sens théorique.
La preuve s’appliquera toujours à toute (petite) catégorie abélienne en raison du théorème d’intégration de Mitchell, qui indique que toute petite catégorie abélienne peut être représentée comme une catégorie de modules sur un anneau.
Pour la catégorie des groupes, transformez simplement toute la notation additive ci-dessous en notation multiplicative et notez que la commutativité du groupe abélien n’est jamais utilisée.
Donc, pour prouver (1), supposons que m et p sont surjectifs et q est injectif.

- Laisser C ′ être un élément de C ′ .
- Depuis p est surjectif, il existe un élément d dans D avec p ( d ) = t ( C ′ ).
- Par commutativité du diagramme, dans ( p ( d )) = q ( J ( d )).
- Puisque je suis t = parce que dans par exactitude, 0 = dans ( t ( C ′ )) = dans ( p ( d )) = q ( J ( d )).
- Depuis q est injectif, J ( d ) = 0, donc d est en ker J = im H .
- Par conséquent, il existe c dans C avec H ( c ) = d .
- Alors t ( n ( c )) = p ( H ( c )) = t ( C ′ ). Depuis t est un homomorphisme, il s’ensuit que t ( C ′ – n ( c )) = 0.
- Par exactitude, C ′ – n ( c ) est à l’image de s , donc il existe B ‘ dans B ‘ avec s ( B ‘ ) = C ′ – n ( c ).
- Depuis m est surjectif, on peut trouver b dans B tel que B ‘ = m ( b ).
- Par commutativité, n ( g ( b )) = s ( m ( b )) = C ′ – n ( c ).
- Depuis n est un homomorphisme, n ( g ( b ) + c ) = n ( g ( b )) + n ( c ) = C ′ – n ( c ) + n ( c ) = C ′ .
- Donc, n est surjectif.
Ensuite, pour prouver (2), supposons que m et p sont injectifs et l est surjectif.

- Laisser c dans C être tel que n ( c ) = 0.
- t ( n ( c )) est alors 0.
- Par commutativité, p ( H ( c )) = 0.
- Depuis p est injectif, H ( c ) = 0.
- Par exactitude, il y a un élément b de B tel que g ( b ) = c .
- Par commutativité, s ( m ( b )) = n ( g ( b )) = n ( c ) = 0.
- Par exactitude, il y a alors un élément un’ de UN’ tel que r ( un’ ) = m ( b ).
- Depuis l est surjectif, il y a un dans UN tel que l ( un ) = un’ .
- Par commutativité, m ( F ( un )) = r ( l ( un )) = m ( b ) .
- Depuis m est injectif, F ( un ) = b .
- Donc c = g ( F ( un )).
- Depuis la composition de g et F est trivial, c = 0.
- Donc, n est injectif.
La combinaison des deux quatre lemmes prouve maintenant les cinq lemmes entiers.
Applications [ modifier ]]
Les cinq lemmes sont souvent appliqués à des séquences exactes longues: lors du calcul de l’homologie ou de la cohomologie d’un objet donné, on utilise généralement un sous-objet plus simple dont l’homologie / la cohomologie est connue et arrive à une séquence exacte longue qui implique les groupes d’homologie inconnus de l’original objet. Cela seul n’est souvent pas suffisant pour déterminer les groupes d’homologie inconnus, mais si l’on peut comparer l’objet et l’objet d’origine à ceux bien compris via des morphismes, alors un morphisme entre les séquences exactes longues respectives est induite, et les cinq lemmes peuvent alors alors être utilisé pour déterminer les groupes d’homologie inconnus.
Voir également [ modifier ]]
Les références [ modifier ]]



Recent Comments