Combien de pendule – Wikipedia wiki

Le Combien de pendule est fondamental pour comprendre les rotations internes entravées en chimie, les caractéristiques quantiques des atomes de diffusion, ainsi que de nombreux autres phénomènes quantiques. Bien qu’un pendule non soumis à l’approximation à petit angle ait une non-linéarité inhérente, l’équation de Schrödinger du système quantifié peut être résolu relativement facilement.

Équation de Schrödinger [ modifier ]]

En utilisant la mécanique lagrangienne de la mécanique classique, on peut développer un hamiltonien pour le système. Un pendule simple a une coordonnée généralisée (le déplacement angulaire

${displaystyle phi}$

) et deux contraintes (la longueur de la chaîne et du plan de mouvement). Les énergies cinétiques et potentielles du système

after-content-x4

${DisplayStyle t = {frac {1} {2}} ml ^ {2} {dot {phi}}} ^ {2},}$

${DisplayStyle u = mgl (1-cos).}$

Il en résulte le hamiltonien

${DisplayStyle {hat {h}} = {frac {{hat {p}}} ^}}} {2ml ^ {2}}}} + mgl (1-COO).}$

L’équation de Schrödinger en fonction du temps pour le système est

${Avis DisplayStyle {frac {dpsi} {dt}} = – {frac {hbar ^ {2}} {2ml ^ {2}}}} {frac {d ^ {2} psi} {dphi ^ {2}} + + Mgl (1-COS Phi) psi.}$

Il faut résoudre l’équation de Schrödinger indépendante du temps pour trouver les niveaux d’énergie et les états propres correspondants. Ceci est mieux accompli en modifiant la variable indépendante comme suit:

${DisplayStyle Eta = Phi + Pi,}$

${DisplayStyle psi = psi e ^ {- iet / hbar},}$

${DisplayStyle epsi = – {frac {hbar ^ {2}} {2ml ^ {2}}} {frac {d ^ {2}} {deta ^ {2}} + mgl (1 + cos eta) psi.}$

C’est simplement l’équation différentielle de Mathieu

${displayStyle {frac {d ^ {2} psi} {deta ^ {2}}} + Left ({frac {2mel ^ {2}} {Hbar ^ {2}}} – {frac {2m ^ {2} Gl ^ {3}} {Hbar ^ {2}}} – {frac {2m ^ {2} gl ^ {3}} {Hbar ^ {2}}} cos eta droit) psi = 0,}$

dont les solutions sont des fonctions Mathieu.

Solutions [ modifier ]]

Énergies [ modifier ]]

Donné

${displayStyle Q}$

, pour de nombreuses valeurs spéciales comptables de

${displaystyle a}$

, appelé valeurs caractéristiques , l’équation de Mathieu admet des solutions périodiques avec une période

${displaystyle 2pi}$

. Les valeurs caractéristiques du cosinus Mathieu, les fonctions sinusoïdales respectivement sont écrites

${displayStyle a_ {n} (q), b_ {n} (q)}$

, où

${displaystyle n}$

est un nombre naturel. Les cas spéciaux périodiques des fonctions de cosinus et de sinus Mathieu sont souvent écrits

${displayStyle ce (n, q, x), se (n, q, x)}$

respectivement, bien qu’ils aient traditionnellement une normalisation différente (à savoir que leur

${displaystyle l ^ {2}}$

norme égale

${displaystyle pi}$

).

Les conditions aux limites du pendule quantique impliquent que

${displayStyle a_ {n} (q), b_ {n} (q)}$

sont les suivants pour une donnée

${displayStyle Q}$

:

${displayStyle {frac {d ^ {2} psi} {deta ^ {2}}} + Left ({frac {2mel ^ {2}} {Hbar ^ {2}}} – {frac {2m ^ {2} Gl ^ {3}} {Hbar ^ {2}}} – {frac {2m ^ {2} gl ^ {3}} {Hbar ^ {2}}} cos eta droit) psi = 0,}$

${displayStyle a_ {n} (q), b_ {n} (q) = {frac {2Mel ^ {2}} {hbar ^ {2}}} – {frac {2m ^ {2} gl ^ {3}} {Hbar ^ {2}}}.}$

Les énergies du système,

${displayStyle e = mgl + {frac {hbar ^ {2} a_ {n} (q), b_ {n} (q)} {2ml ^ {2}}}}$

Pour les solutions uniques / impaises respectivement, sont quantifiées en fonction des valeurs caractéristiques trouvées en résolvant l’équation de Mathieu.

La profondeur potentielle effective peut être définie comme

${displayStyle q = {frac {m ^ {2} gl ^ {3}} {hbar ^ {2}}}.}$

Un potentiel profond donne la dynamique d’une particule dans un potentiel indépendant. En revanche, dans un potentiel peu profond, les ondes Bloch, ainsi que les tunnels quantiques, deviennent importantes.

Solution générale [ modifier ]]

La solution générale de l’équation différentielle ci-dessus pour une valeur donnée de un et q est un ensemble de cosinus Mathieu linéairement indépendants et de SINES MATHIE, qui sont des solutions uniques et étranges respectivement. En général, les fonctions Mathieu sont apériodiques; Cependant, pour les valeurs caractéristiques de

${displayStyle a_ {n} (q), b_ {n} (q)}$

, le cosinus de Mathieu et le sinus deviennent périodiques avec une période de

${displaystyle 2pi}$

.

Auto-staté [ modifier ]]

Pour des valeurs positives de q , ce qui suit est vrai:

${displayStyle c (a_ {n} (q), q, x) = {frac {ce (n, q, x)} {ce (n, q, 0)}},}$

${displayStyle s (b_ {n} (q), q, x) = {frac {se (n, q, x)} {se ‘(n, q, 0)}}.}$

Voici les premières fonctions de cosinus Mathieu périodiques pour

${displayStyle q = 1}$

.

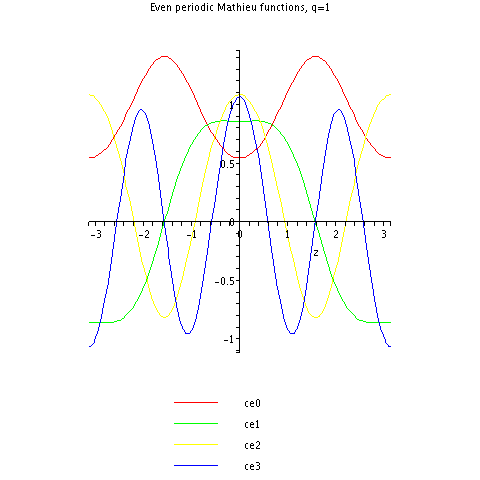
Notez que, par exemple,

${displayStyle ce (1,1, x)}$

(vert) ressemble à une fonction de cosinus, mais avec des collines plus plates et des vallées moins profondes.

Voir également [ modifier ]]

Bibliographie [ modifier ]]

• Bransden, B. H.; Joachain, C. J. (2000). Mécanique quantique (2e éd.). Essex: Pearson Education. ISBN 0-582-35691-1 .
• Davies, John H. (2006). La physique des semi-conducteurs de faible dimension: une introduction (6e réimpression éd.). La presse de l’Universite de Cambridge. ISBN 0-521-48491-X .
• Griffiths, David J. (2004). Introduction à la mécanique quantique (2e éd.). Prentice Hall. ISBN 0-13-111892-7 .
• Muhammad Ayub, Atom Optics Quantum Pendule , 2011, Islamabad, Pakistan., https://arxiv.org/abs/1012.6011