Expansion de la série – Wikipedia wiki

Posted on by
before-content-x4

Un article de Wikipédia, l’encyclopédie libre

after-content-x4

Expression d’une fonction comme une somme infinie de fonctions plus simples

Approximation of cosine by a Taylor series

En mathématiques, un Expansion de la série est une technique qui exprime une fonction comme une somme infinie ou une série de fonctions plus simples. Il s’agit d’une méthode pour calculer une fonction qui ne peut pas être exprimée par des opérateurs élémentaires seulement (addition, soustraction, multiplication et division). [d’abord]

Le soi-disant résultant série Souvent, peut être limité à un nombre fini de termes, donnant ainsi une approximation de la fonction. Plus les termes de la séquence sont utilisés, plus cette approximation sera simple. Souvent, l’inexactitude qui en résulte (c’est-à-dire la somme partielle des termes omises) peut être décrite par une équation impliquant une grande notation O (voir également l’expansion asymptotique). L’expansion de la série sur un intervalle ouvert sera également une approximation des fonctions non analytiques. [2] [ Vérification nécessaire ]]

Types d’expansions en série [ modifier ]]

Il existe plusieurs types d’expansions en série, répertoriées ci-dessous.

UN Série Taylor est une série de puissance basée sur les dérivés d’une fonction en un seul point. [3] Plus précisément, si une fonction

F : DANS → R {displaystyle f: uto mathbb {r}}

est infiniment différenciable autour d’un point

after-content-x4
X 0{displayStyle x_ {0}}

, puis la série Taylor de F Autour de ce point est donné par

∑ n=0∞f(n)(x0)n!( X – X 0) n{TextStyle Sum _ {n = 0} ^ {Inty} {frac {f ^ {(n)} (x_ {0})}}} (x-x_ {0}) ^ {n}}

sous la convention

0 0: = d’abord {DisplayStyle 0 ^ {0}: = 1}

. [3] [4] Le Série Maclaurin d’un F est sa série Taylor sur

X 0= 0 {displayStyle x_ {0} = 0}

. [5] [4] UN Série Laurent est une généralisation de la série Taylor, permettant des valeurs d’exposants négatives; il prend la forme

∑ k=−∞∞c k( Avec – un ) k{textstyle sum _ {k = -infty} ^ {nourrissons} c_ {k} (z-a) ^ {k}}

et converge dans un anneau. [6]

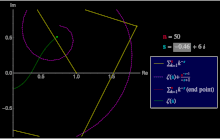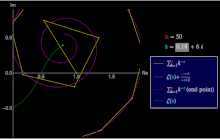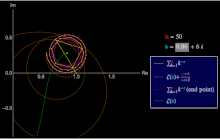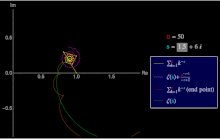
spiral representing partial sums of the Dirichlet series defining the Riemann zeta function

Convergence et divergence des sommes partielles de la série Dirichlet définissant la fonction Riemann Zeta. Ici, la ligne jaune représente les cinquante premiers sommes partielles successives

UN série générale Dirichlet est une série de la forme

∑ n=1∞un nC’est −λns. {Textstyle sum _ {n = 1} ^ {Inty} a_ {n} e ^ {- lambda _ {n}.}.}

Un cas particulier important est le série de Dirichlet ordinaire

∑ n=1∞anns. {Textstyle sum _ {n = 1} ^ {Inty} {frac {a_ {n}} {n ^ {s}}.}

[7] Utilisé dans la théorie des nombres. [ citation requise ]]

UN Série de Fourier est une expansion des fonctions périodiques comme une somme de nombreuses fonctions sinus et cosinus. [8] Plus précisément, la série Fourier d’une fonction

F ( t ) {displayStyle f (t)}

de période

2 L {displayStyle 2L}

est donné par l’expression

où les coefficients sont donnés par les formules [8] [9]

En acoustique, par exemple, le ton fondamental et les connotations forment ensemble un exemple d’une série de Fourier. [ citation requise ]]

Série newtonienne [ citation requise ]]

Legendre Polynomials: Utilisé en physique pour décrire un champ électrique arbitraire comme superposition d’un champ dipolaire, un champ quadrupol, un champ d’octupole, etc. [ citation requise ]]

Zernike Polynomials: Utilisé en optique pour calculer les aberrations des systèmes optiques. Chaque terme de la série décrit un type particulier d’aberration. [ citation requise ]]

L’erreur relative dans une série Stirling tronquée Vs. n , pour 0 à 5 termes. Les plis dans les courbes représentent des points où la série tronquée coïncide avec

Le Série Stirling

est une approximation de la fonction log-gamma. [dix]

Exemples [ modifier ]]

Ce qui suit est la série Taylor de

C’est x{displaystyle e ^ {x}}

:

[11] [douzième]

La série Dirichlet de la fonction Riemann Zeta est

[7]

Les références [ modifier ]]

  1. ^ “Série et extensions” . Mathematics Libertexts . 2013-11-11-07 . Récupéré 2021-12-24 .
  2. ^ Gil, Amparo; Segura, Javier; Temme, Nico M. (2007-01-01). Méthodes numériques pour les fonctions spéciales . Siam. ISBN 978-0-89871-782-2 .
  3. ^ un b “Taylor Series – Encyclopedia of Mathematics” . Encyclopediaofmath.org . 27 décembre 2013 . Récupéré 22 mars 2022 .
  4. ^ un b Edwards, C. Henry; Penney, David E. (2008). Équations différentielles élémentaires avec problèmes de valeur limite . p. 196. ISBN 978-0-13-600613-8 .
  5. ^ Weepstein, Eric W. “Série Maclaurin” . mathworld.wolfram.com . Récupéré 2022-03-22 .
  6. ^ “Laurent Series – Encyclopedia of Mathematics” . Encyclopediaofmath.org . Récupéré 2022-03-22 .
  7. ^ un b “Dirichlet Series – Encyclopedia of Mathematics” . Encyclopediaofmath.org . 26 janvier 2022 . Récupéré 22 mars 2022 .
  8. ^ un b “Fourier Series – Encyclopedia of Mathematics” . Encyclopediaofmath.org . Récupéré 2022-03-22 .
  9. ^ Edwards, C. Henry; Penney, David E. (2008). Équations différentielles élémentaires avec problèmes de valeur limite . Pp. 558, 564. ISBN 978-0-13-600613-8 .
  10. ^ “DLMF: 5.11 Expansions asymptotiques” . dlmf.nist.gov . Récupéré 22 mars 2022 .
  11. ^ Weepstein, Eric W. “Fonction exponentielle” . mathworld.wolfram.com . Récupéré 2021-08-12 .
  12. ^ “Fonction exponentielle – Encyclopédie des mathématiques” . Encyclopediaofmath.org . 5 juin 2020 . Récupéré 12 août 2021 . {{cite web}} : CS1 MAINT: URL-statut (lien)

after-content-x4