Transversalität (Mathematik) – Wikipedia

In Mathematik, Transversalität ist ein Begriff, der beschreibt, wie sich Räume schneiden können; Transversalität kann als die gesehen werden “Gegenteil” von Tangentialität und spielt eine Rolle in der allgemeinen Position. Es formalisiert die Idee eines generischen Schnittpunkts in der Differentialtopologie. Es wird definiert, indem die Linearisierungen der Schnitträume an den Schnittpunkten berücksichtigt werden.

Definition[edit]

Querkurven auf der Oberfläche einer Kugel

Nichtquerkurven auf der Oberfläche einer Kugel

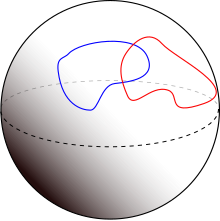
Es wird gesagt, dass zwei Untervielfalt eines gegebenen endlichdimensionalen glatten Verteilers quer schneiden Wenn an jedem Schnittpunkt ihre getrennten Tangentenräume an diesem Punkt zusammen den Tangentenraum des Umgebungsverteilers an diesem Punkt erzeugen.^[1] Verteiler, die sich nicht schneiden, sind leer quer. Wenn die Verteiler eine komplementäre Dimension haben (dh ihre Abmessungen addieren sich zur Dimension des Umgebungsraums), bedeutet die Bedingung, dass der Tangentenraum zum Umgebungsverteiler die direkte Summe der beiden kleineren Tangentenräume ist. Wenn ein Schnittpunkt quer verläuft, ist der Schnittpunkt eine Untervielfalt, deren Codimension gleich den Summen der Codimensionen der beiden Mannigfaltigkeiten ist. In Abwesenheit der Transversalitätsbedingung kann es sein, dass der Schnittpunkt keine Untervielfalt ist und eine Art singulären Punkt aufweist.

Dies bedeutet insbesondere, dass sich transversale Untervielfaltigkeiten mit komplementärer Dimension in isolierten Punkten (dh einer 0-Mannigfaltigkeit) schneiden. Wenn beide Teilverteiler und der Umgebungsverteiler ausgerichtet sind, ist ihr Schnittpunkt ausgerichtet. Wenn der Schnittpunkt nulldimensional ist, ist die Ausrichtung einfach ein Plus oder Minus für jeden Punkt.

Eine Notation für den Querschnitt zweier Untervielfalt

und

einer gegebenen Mannigfaltigkeit

ist

. Diese Notation kann auf zwei Arten gelesen werden: entweder als „

und

quer schneiden “oder als alternative Notation für den satztheoretischen Schnitt

von

und

wenn dieser Schnitt quer ist. In dieser Notation lautet die Definition von Transversalität

${ displaystyle L_ {1} Pitchfork L_ {2} iff forall p in L_ {1} cap L_ {2}, T_ {p} M = T_ {p} L_ {1} + T_ {p} L_ {2}.}$

Transversalität von Karten[edit]

Der Begriff der Transversalität eines Paares von Submanifolds lässt sich leicht auf die Transversalität eines Submanifolds und eine Karte auf den Umgebungsverteiler oder auf ein Paar von Karten auf den Umgebungsverteiler erweitern, indem gefragt wird, ob die Vorwärtsbewegung der Tangentenräume entlang des Vorbilds von Punkten erfolgt der Schnittpunkt der Bilder erzeugen den gesamten Tangentenraum des Umgebungsverteilers.^[2] Wenn es sich bei den Karten um Einbettungen handelt, entspricht dies der Transversalität der Untervielfalt.

Bedeutung der Transversalität für verschiedene Dimensionen[edit]

Die Transversalität hängt vom Umgebungsraum ab. Die beiden gezeigten Kurven sind quer, wenn sie als in die Ebene eingebettet betrachtet werden, aber nicht, wenn wir sie als in eine Ebene im dreidimensionalen Raum eingebettet betrachten

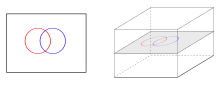
Angenommen, wir haben Querkarten

und

wo

und

sind Verteiler mit Abmessungen

und

beziehungsweise.

Die Bedeutung der Transversalität unterscheidet sich stark in Abhängigkeit von den relativen Dimensionen von

und

. Die Beziehung zwischen Transversalität und Tangentialität ist am klarsten, wenn

.

Wir können drei verschiedene Fälle betrachten:

1. Wann
   ${ displaystyle ell _ {1} + ell _ {2}$

   ist es unmöglich für das Bild von

   ${ displaystyle L_ {1}}$

   und

   ${ displaystyle L_ {2}}$

   ‘s Tangentenräume zu überspannen

   ${ displaystyle M}$

   ‘s Tangentenraum an jedem Punkt. Also jeder Schnittpunkt zwischen

   ${ displaystyle f_ {1}}$

   und

   ${ displaystyle f_ {2}}$

   kann nicht quer sein. Nicht schneidende Verteiler erfüllen jedoch vakuum die Bedingung, so dass gesagt werden kann, dass sie sich quer schneiden.

2. Wann
   ${ displaystyle ell _ {1} + ell _ {2} = m}$

   , Das Bild von

   ${ displaystyle L_ {1}}$

   und

   ${ displaystyle L_ {2}}$

   Die Tangentenräume müssen sich direkt summieren

   ${ displaystyle M}$

   Tangentenraum an jedem Schnittpunkt. Ihr Schnittpunkt besteht somit aus isolierten vorzeichenbehafteten Punkten, dh einer nulldimensionalen Mannigfaltigkeit.

3. Wann
   ${ displaystyle ell _ {1} + ell _ {2}> m}$

   

   ${ displaystyle f_ {1}}$

   und

   ${ displaystyle f_ {2}}$

   sind Eintauchungen an ihrem Schnittpunkt, wie dies bei eingebetteten Untervielfalt der Fall ist. Wenn es sich bei den Karten um Immersionen handelt, ist der Schnittpunkt ihrer Bilder vielfältig

   ${ displaystyle ell _ {1} + ell _ {2} -m.}$

   

Schnittprodukt[edit]

Bei zwei beliebigen glatten Untervielfaltigkeiten ist es möglich, eine von beiden um einen beliebig kleinen Betrag zu stören, so dass sich die resultierende Untervielfalt quer zur festen Untervielfalt schneidet. Solche Störungen wirken sich nicht auf die Homologieklasse der Mannigfaltigkeiten oder ihrer Schnittpunkte aus. Wenn sich beispielsweise Verteiler mit komplementärer Dimension quer schneiden, ändert sich die vorzeichenbehaftete Summe der Anzahl ihrer Schnittpunkte nicht, selbst wenn wir die Verteiler zu einem anderen Querschnitt isotopieren. (Die Schnittpunkte können modulo 2 gezählt werden, wobei die Vorzeichen ignoriert werden, um eine gröbere Invariante zu erhalten.) Dies führt zu einem bilinearen Schnittprodukt für Homologieklassen jeder Dimension, das Poincaré dual zum Becherprodukt für die Kohomologie ist. Wie das Becherprodukt ist das Schnittprodukt abgestuft-kommutativ.

Beispiele für Querschnittpunkte[edit]

Das einfachste nicht triviale Beispiel für Transversalität sind Bögen in einer Oberfläche. Ein Schnittpunkt zwischen zwei Bögen ist genau dann quer, wenn es sich nicht um eine Tangentialität handelt, dh ihre Tangentenlinien innerhalb der Tangentialebene zur Oberfläche sind unterschiedlich.

In einem dreidimensionalen Raum schneiden sich Querkurven nicht. Kurven quer zu Flächen schneiden sich in Punkten, und Flächen quer zueinander schneiden sich in Kurven. Kurven, die eine Oberfläche an einem Punkt tangieren (z. B. auf einer Oberfläche liegende Kurven), schneiden die Oberfläche nicht quer.

Hier ist ein spezielleres Beispiel: Nehmen wir an, dass

ist eine einfache Lügengruppe und

ist seine Lie-Algebra. Nach dem Jacobson-Morozov-Theorem jedes nilpotente Element

kann in eine aufgenommen werden

-verdreifachen

. Die Darstellungstheorie von

sagt uns das

. Der Raum

ist der Tangentenraum bei

zur angrenzenden Umlaufbahn

und so der affine Raum

schneidet die Umlaufbahn von

quer. Der Raum

ist bekannt als die “Slodowy Scheibe” nach Peter Slodowy.

Anwendungen[edit]

Optimale Kontrolle[edit]

In Feldern, die die Variationsrechnung oder das verwandte Pontryagin-Maximalprinzip verwenden, wird die Transversalitätsbedingung häufig verwendet, um die Arten von Lösungen zu steuern, die bei Optimierungsproblemen gefunden werden. Zum Beispiel ist es eine notwendige Bedingung für Lösungskurven für Probleme der Form:

Minimieren

${ displaystyle int {F (x, y, y ^ { prime})} dx}$

wobei einer oder beide Endpunkte der Kurve nicht festgelegt sind.

Bei vielen dieser Probleme erfüllt die Lösung die Bedingung, dass die Lösungskurve die Nulllinie oder eine andere Kurve, die die Endbedingungen beschreibt, quer kreuzt.

Glätte der Lösungsräume[edit]

Mit dem Satz von Sard, dessen Hypothese ein Sonderfall der Transversalität von Karten ist, kann gezeigt werden, dass Querschnitte zwischen Untervielfaltigkeiten eines Raums komplementärer Dimensionen oder zwischen Untervielfaltigkeiten und Karten zu einem Raum selbst glatte Untervielfaltigkeiten sind. Zum Beispiel, wenn ein glatter Abschnitt des Tangentenbündels einer orientierten Mannigfaltigkeit – dh ein Vektorfeld – als Karte von der Basis zum Gesamtraum betrachtet wird und den Nullabschnitt (entweder als Karte oder als Untervielfalt betrachtet) quer schneidet dann bildet die Nullmenge des Abschnitts – dh die Singularitäten des Vektorfeldes – eine glatte 0-dimensionale Untervielfalt der Basis, dh eine Menge von vorzeichenbehafteten Punkten. Die Vorzeichen stimmen mit den Indizes des Vektorfeldes überein, und daher ist die Summe der Vorzeichen – dh die Grundklasse der Nullmenge – gleich der Euler-Charakteristik der Mannigfaltigkeit. Allgemeiner ist für ein Vektorbündel über einem orientierten glatten geschlossenen endlichen Verteiler die Nullmenge eines Abschnitts quer zum Nullabschnitt eine Untervielfalt der Basis der Codimension, die dem Rang des Vektorbündels und seiner Homologieklasse entspricht wird Poincaré dual zur Euler-Klasse des Bundles sein.

Ein ganz besonderer Fall hierfür ist der folgende: Wenn eine differenzierbare Funktion von Real zu Real eine Ableitung ungleich Null bei einer Null der Funktion hat, ist die Null einfach, dh der Graph ist quer zur x-Achse bei dieser Null; Eine Nullableitung würde eine horizontale Tangente an die Kurve bedeuten, die mit dem Tangentenraum an die Kurve übereinstimmt x-Achse.

Für ein unendlichdimensionales Beispiel ist der D-Bar-Operator ein Abschnitt eines bestimmten Banach-Raumbündels über den Raum von Karten von einer Riemann-Oberfläche in eine fast komplexe Mannigfaltigkeit. Die Nullmenge dieses Abschnitts besteht aus holomorphen Karten. Wenn gezeigt werden kann, dass der D-Bar-Operator quer zum Nullabschnitt verläuft, ist dieser Modulraum ein glatter Verteiler. Diese Überlegungen spielen eine grundlegende Rolle in der Theorie der pseudoholomorphen Kurven und der Gromov-Witten-Theorie. (Beachten Sie, dass für dieses Beispiel die Definition der Transversalität verfeinert werden muss, um mit Banach-Räumen umgehen zu können!)

Grammatik[edit]

“Transversal” ist ein Substantiv; das Adjektiv ist “quer.”

Zitat von JHC Whitehead, 1959^[3]

Siehe auch[edit]

Verweise[edit]