atan2 – Wikipedia

Posted on December 24, 2020 by lordneo

before-content-x4

atan2 (y, x)

gibt den Winkel zurück

θ

zwischen dem Strahl auf den Punkt

((x, y)

und das Positive x Achse, beschränkt auf

(- π, π]]

Grafik von

{ displaystyle operatorname {atan2} (y, x)}

Die Funktion

{ displaystyle operatorname {atan2} (y, x)}

${ displaystyle operatorname {atan2} (y, x)}$ oder

{ displaystyle operatorname {arctan2} (y, x)}

${ displaystyle operatorname {arctan2} (y, x)}$ (von “2-Argument-Arkustangens”) ist definiert als der Winkel in der euklidischen Ebene im Bogenmaß zwischen dem Positiv x Achse und der Strahl zum Punkt $((x, y) \neq (0, 0)$ .

Die Funktion

{ displaystyle operatorname {atan2} (y, x)}

${ displaystyle operatorname {atan2} (y, x)}$ erschien erstmals in der Programmiersprache Fortran (in der IBM-Implementierung FORTRAN-IV im Jahr 1961). Es war ursprünglich beabsichtigt, einen korrekten und eindeutigen Wert für den Winkel zurückzugeben $θ$ beim Konvertieren von kartesischen Koordinaten $((x, y)$ zu Polarkoordinaten $((r, θ)$ .

Gleichermaßen

{ displaystyle operatorname {atan2} (y, x)}

${ displaystyle operatorname {atan2} (y, x)}$ ist das Argument (auch genannt Phase oder Winkel) der komplexen Zahl

{ displaystyle x + iy.}

${ displaystyle x + iy.}$

{ displaystyle operatorname {atan2} (y, x)}

${ displaystyle operatorname {atan2} (y, x)}$ gibt einen einzelnen Wert zurück $θ$ so dass $- - π < θ \leq π$ und für einige $r > 0$ ,

{ displaystyle { begin {align} x & = r cos theta, \ y & = r sin theta. end {align}}}

Während es wahr ist, dass

{ displaystyle r = { sqrt {x ^ {2} + y ^ {2}}}}

${ displaystyle r = { sqrt {x ^ {2} + y ^ {2}}}}$ gilt nicht immer folgende Äquivalenz:

{ displaystyle theta = arctan left ({ frac {y} {x}} right).}

Dies gilt nur wenn $x > 0$ . Wann $x <0$ zeigt der Winkel, der aus dem obigen Ausdruck hervorgeht, in die entgegengesetzte Richtung des korrekten Winkels und einen Wert von $π$ (oder 180 °) muss entweder addiert oder subtrahiert werden $θ$ um den kartesischen Punkt zu setzen $((x, y)$ in den richtigen Quadranten der euklidischen Ebene.^[1] Dies erfordert die Kenntnis der Zeichen von $x$ und $y$ separat, welche Informationen verloren gehen, wenn $y$ wird geteilt durch $x$ .

Da jedes ganzzahlige Vielfache von $2 π$ kann dem Winkel hinzugefügt werden $θ$ ohne sich zu ändern $x$ oder $y$ Dies impliziert einen mehrdeutigen Wert für den zurückgegebenen Wert, den Hauptwert des Winkels, in dem Intervall $(- π, π]]$ ist zurück gekommen. $θ$ ist signiert, wobei die Winkel gegen den Uhrzeigersinn positiv und der Uhrzeigersinn negativ sind. Speziell,

{ displaystyle operatorname {atan2} (y, x)}

${ displaystyle operatorname {atan2} (y, x)}$ ist in der Pause $[0, π]$ wann $y \geq 0$ , und in $(- π, 0)$ wann $y <0$ .

Table of Contents

Geschichte und Motivation[edit]

Graph der Tangentenfunktion von –

π

zu +

π

mit den entsprechenden Zeichen von y/.x. Die grünen Pfeile zeigen auf die Ergebnisse von atan2 (−1, −1) und atan2 (1, 1).

Das $atan2$ Die Funktion wurde zuerst in Computerprogrammiersprachen eingeführt, ist aber jetzt auch in anderen Bereichen der Wissenschaft und Technik üblich. Es reicht mindestens bis zur Programmiersprache FORTRAN zurück^[2]

und ist derzeit in vielen modernen Programmiersprachen zu finden. Zu diesen Sprachen gehören: die math.h-Standardbibliothek von C, die Java Math-Bibliothek, System.Math von .NET (verwendbar von C #, VB.NET usw.), das Python-Mathematikmodul, das Ruby Math-Modul und das Go-Mathematikpaket^[3] und anderswo. Darüber hinaus enthalten viele Skriptsprachen wie Perl den C-Stil atan2(y, x) Funktion.

Die Arktangensfunktion mit einem Argument kann nicht zwischen diametral entgegengesetzten Richtungen unterscheiden. Zum Beispiel der Winkel gegen den Uhrzeigersinn von der $x$ Achse zum Vektor $(1, 1)$ , berechnet in üblicher Weise als $Arctan (1/1)$ ist $π / 4$ (Bogenmaß) oder $45 °$ . Der Winkel zwischen dem $x$ Achse und der Vektor $(-1, -1)$ scheint nach der gleichen Methode zu sein $Arctan (-1 / -1)$ , nochmal $π / 4$ , obwohl man die Antworten erwarten könnte $-3π / 4$ (–135 °) oder $5π / 4$ (225 °). Außerdem wird versucht, den Winkel zwischen dem $x$ Achse und die Vektoren $(0, y), y \neq 0$ erfordert eine Bewertung von $arctan (y / 0)$ , was bei Division durch Null fehlschlägt.

Das $atan2$ Die Funktion berechnet aus zwei Variablen einen eindeutigen Bogen-Tangentenwert $y$ und $x$ , wobei die Vorzeichen beider Argumente verwendet werden, um den Quadranten des Ergebnisses zu bestimmen, wodurch der gewünschte Zweig der Bogen-Tangente von ausgewählt wird $y /. x$ , z.B, $atan2 (1, 1) = π / 4$ und $atan2 (-1, -1) = -3π / 4$ . Ähnlich z. $atan2 (1, 0) = π / 2$ .

Wenn Berechnungen manuell durchgeführt werden, können die erforderlichen Quadrantenkorrekturen und die Ausnahmebehandlung durch Inspektion durchgeführt werden. Es ist jedoch sinnvoller, eine einzige Funktion zu haben, die immer ein eindeutig korrektes Ergebnis liefert. Das $atan2$ Die Funktion ist in vielen Anwendungen nützlich, die Vektoren im euklidischen Raum betreffen, z. B. beim Ermitteln der Richtung von einem Punkt zum anderen. Eine Hauptanwendung sind Computergrafikrotationen zum Konvertieren von Rotationsmatrixdarstellungen in Eulerwinkel.

Definition und Berechnung[edit]

Die Funktion $atan2$ berechnet den Hauptwert der Argumentfunktion, die auf die komplexe Zahl angewendet wird $x + y ich$ . Das ist, $atan2 (y, x) = Pr arg (x + y i) = Arg (x + y ich)$ . Das Argument könnte durch ein beliebiges Vielfaches von geändert werden $2π$ (entsprechend einer vollständigen Drehung um den Ursprung) ohne den Winkel zu verändern, sondern zu definieren $atan2$ eindeutig verwendet man den Hauptwert im Bereich

{ displaystyle (- pi, pi]}

${ displaystyle (- pi, pi]}$ , das ist, $- - π y, x) \leq π$ .

In Bezug auf den Standard $Arctan$ Funktion, deren Reichweite ist $(-π / 2, π / 2)$ kann wie folgt ausgedrückt werden:

{ displaystyle operatorname {atan2} (y, x) = { begin {case} arctan ({ frac {y} {x}}) & { text {if}} x> 0, \ arctan ({ frac {y} {x}}) + pi & { text {if}} x <0 { text {und}} y geq 0, \ arctan ({ frac {y} { x}}) - pi & { text {if}} x <0 { text {und}} y<0,\+{frac {pi }{2}}&{text{if }}x=0{text{ and }}y>0, \ – { frac { pi} {2}} & { text {if}} x = 0 { text {und}} y <0, \ { text {undefined}} & { text {if}} x = 0 { text {und}} y = 0. end {case}}}

Ein kompakter Ausdruck mit vier überlappenden Halbebenen ist

{ displaystyle operatorname {atan2} (y, x) = { begin {case} arctan left ({ frac {y} {x}} right) & { text {if}} x> 0, \ { frac { pi} {2}} – arctan left ({ frac {x} {y}} right) & { text {if}} y> 0, \ – { frac { pi} {2}} – arctan left ({ frac {x} {y}} right) & { text {if}} y <0, \ arctan left ({ frac { y} {x}} right) pm pi & { text {if}} x <0, \ { text {undefined}} & { text {if}} x = 0 { text {und }} y = 0. end {Fälle}}}

Die Iverson-Klammer-Notation ermöglicht einen noch kompakteren Ausdruck:

${ displaystyle operatorname {atan2} (y, x)}$	${ displaystyle = arctan left ({ frac {y} {x}} right)[xneq 0]+ operatorname {sgn} (y) left ( pi [x<0]+ { frac { pi} {2}}[x=0]Recht)}$
	${ displaystyle + ; { text {undefined}} ; ![x=0wedge y=0]}}$

Formel ohne offensichtliches bedingtes Konstrukt:

{ displaystyle operatorname {atan2} (y, x) = operatorname {sgn} (x) ^ {2} arctan left ({ frac {y} {x}} right) + { frac {1 – operatorname {sgn} (x)} {2}} left (1+ operatorname {sgn} (y) – operatorname {sgn} (y) ^ {2} right) pi}

Der folgende Ausdruck, der aus der Tangentenhalbwinkelformel abgeleitet ist, kann ebenfalls zum Definieren verwendet werden $atan2$ ::

{ displaystyle operatorname {atan2} (y, x) = { begin {case} 2 arctan left ({ frac {y} {{ sqrt {x ^ {2} + y ^ {2}}} + x}} right) & { text {if}} x> 0 { text {oder}} y neq 0, \ pi & { text {if}} x <0 { text {und }} y = 0, \ { text {undefined}} & { text {if}} x = 0 { text {und}} y = 0. end {case}}}

Dieser Ausdruck ist möglicherweise besser für die symbolische Verwendung geeignet als die obige Definition. Es ist jedoch für die allgemeine Verwendung von Gleitkomma-Berechnungen ungeeignet, da Rundungsfehler auftreten

{ displaystyle { sqrt {x ^ {2} + y ^ {2}}}}

$sqrt {x ^ 2 + y ^ 2}$ in der Nähe der Region erweitern $x <0, y = 0$ (Dies kann sogar zu einer Teilung von führen y um Null).

Eine Variante der letzten Formel, die diese aufgeblasenen Rundungsfehler vermeidet:

{ displaystyle operatorname {atan2} (y, x) = { begin {case} 2 arctan left ({ frac {y} {{ sqrt {x ^ {2} + y ^ {2}}} + x}} right) & { text {if}} x> 0, \ 2 arctan left ({ frac {{ sqrt {x ^ {2} + y ^ {2}}} – x } {y}} right) & { text {if}} x leq 0 { text {und}} y neq 0, \ pi & { text {if}} x <0 { text {und}} y = 0, \ { text {undefined}} & { text {if}} x = 0 { text {und}} y = 0. end {case}}}

Die Ableitung des Hauptwerts des Arguments bezieht sich auf diese Zahl

Anmerkungen:

Dies führt zu Ergebnissen im Bereich $(-π, π]$ .^{[note 2]}
Wie oben erwähnt, der Hauptwert des Arguments $atan2 (y, x)$ kann verwandt sein mit $arctan (y /. x)$ durch Trigonometrie. Die Ableitung lautet wie folgt:

Wenn

((x, y) = (r cos θ, r Sünde θ)

, dann

bräunen(θ / 2) = y / ((r + x)

. Es folgt dem

{ displaystyle { text {atan2}} (y, x) = theta = 2 , theta / 2 = 2 arctan { frac {y} {{ sqrt {x ^ {2} + y ^ { 2}}} + x}}.}

Beachten Sie, dass

\sqrt x 2 + y 2 + x \neq 0

in der fraglichen Domäne.

Derivat[edit]

Als die Funktion $atan2$ ist eine Funktion von zwei Variablen, es hat zwei partielle Ableitungen. An Punkten, an denen diese Derivate existieren, $atan2$ ist bis auf eine Konstante gleich $arctan (y /. x)$ . Daher für $x > 0$ oder $y \neq 0$ ,

{ displaystyle { begin {align} & { frac { partielle} { partielle x}} operatorname {atan2} (y, , x) = { frac { partielle} { partielle x}} arctan left ({ frac {y} {x}} right) = – { frac {y} {x ^ {2} + y ^ {2}}}, \[5pt]& { frac { partiell} { partiell y}} operatorname {atan2} (y, , x) = { frac { partiell} { partiell y}} arctan left ({ frac {y } {x}} right) = { frac {x} {x ^ {2} + y ^ {2}}}. end {align}}}

Somit ist der Gradient von atan2 gegeben durch

{ displaystyle nabla { text {atan2}} (y, x) = left ({- y über x ^ {2} + y ^ {2}}, {x über x ^ {2} + y ^ {2}} right).}

Informelle Darstellung der Funktion $atan2$ als Winkelfunktion $θ ((x, y) = atan2 (y, x)$ (die nur bis zu einer Konstanten definiert ist) ergibt die folgende Formel für das Gesamtdifferential:

{ displaystyle { begin {align} mathrm {d} theta & = { frac { partiell} { partiell x}} operatorname {atan2} (y, , x) , mathrm {d} x + { frac { partiell} { partiell y}} operatorname {atan2} (y, , x) , mathrm {d} y \[5pt]& = – { frac {y} {x ^ {2} + y ^ {2}} , mathrm {d} x + { frac {x} {x ^ {2} + y ^ {2}} } , mathrm {d} y. end {align}}}

Während der Funktion $atan2$ ist entlang des Negativs diskontinuierlich $x$ -Achse, die die Tatsache widerspiegelt, dass der Winkel nicht kontinuierlich definiert werden kann, diese Ableitung wird kontinuierlich definiert, außer am Ursprung, was die Tatsache widerspiegelt, dass infinitesimal (und tatsächlich lokal) Änderungen im Winkel kann überall außer dem Ursprung definiert werden. Das Integrieren dieser Ableitung entlang eines Pfades ergibt die gesamte Änderung des Winkels über den Pfad, und das Integrieren über eine geschlossene Schleife ergibt die Wicklungszahl.

In der Sprache der Differentialgeometrie ist diese Ableitung eine Einform und sie ist geschlossen (ihre Ableitung ist Null), aber nicht genau (sie ist nicht die Ableitung einer 0-Form, dh einer Funktion), und tatsächlich erzeugt die erste de Rham-Kohomologie der punktierten Ebene. Dies ist das grundlegendste Beispiel für eine solche Form und für die Differentialgeometrie von grundlegender Bedeutung.

Die partiellen Ableitungen von $atan2$ enthalten keine trigonometrischen Funktionen, was sie besonders in vielen Anwendungen (z. B. eingebetteten Systemen) nützlich macht, in denen die Bewertung trigonometrischer Funktionen teuer sein kann.

Abbildungen[edit]

Diese Abbildung zeigt Werte von atan2 entlang ausgewählter Strahlen vom Ursprung, die am Einheitskreis markiert sind. Die Werte im Bogenmaß werden innerhalb des Kreises angezeigt. Das Diagramm verwendet die mathematische Standardkonvention, dass die Winkel entlang des Strahls nach rechts von Null gegen den Uhrzeigersinn zunehmen. Beachten Sie, dass die Reihenfolge der Argumente umgekehrt ist. die Funktion $atan2 (y, x)$ berechnet den dem Punkt entsprechenden Winkel $((x, y)$ .

Vergleich der Funktionen von Arctan und Atan2

Diese Abbildung zeigt die Werte von

{ displaystyle arctan ( tan ( theta))}

${ displaystyle arctan ( tan ( theta))}$ zusammen mit

{ displaystyle operatorname {atan2} ( sin ( theta), cos ( theta))}

${ displaystyle operatorname {atan2} ( sin ( theta), cos ( theta))}$ zum

{ displaystyle 0 leq theta leq 2 pi}

${ displaystyle 0 leq theta leq 2 pi}$ . Beide Funktionen sind ungerade und periodisch mit Perioden

{ displaystyle pi}

$Pi$ und

{ displaystyle 2 pi}

$2 pi$ und kann somit leicht zu jedem Bereich realer Werte von ergänzt werden

{ displaystyle theta}

$Theta$ . Man kann deutlich die Astschnitte der sehen

{ displaystyle operatorname {atan2}}

${ displaystyle operatorname {atan2}}$ -Funktion bei

{ displaystyle theta = pi}

$theta = pi$ und von der

{ displaystyle arctan}

$arctan$ -Funktion bei

{ displaystyle theta in {{ tfrac { pi} {2}}, ; { tfrac {3 pi} {2}} }}

${ displaystyle theta in {{ tfrac { pi} {2}}, ; { tfrac {3 pi} {2}} }}$ .^[4]

Die beiden folgenden Abbildungen zeigen jeweils 3D-Ansichten $atan2 (y, x)$ und $arctan (y /. x)$ über einen Bereich des Flugzeugs. Beachten Sie, dass für $atan2 (y, x)$ , Strahlen in dem X./.Y.-Ebene, die vom Ursprung ausgeht, hat konstante Werte, aber für $arctan (y /. x)$ Linien in dem X./.Y.-Ebene, die durch den Ursprung geht, haben konstante Werte. Zum $x > 0$ geben die beiden Diagramme identische Werte an.

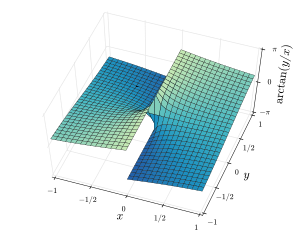
Winkelsumme und Differenzidentität[edit]

Summen von

{ displaystyle operatorname {atan2}}

${ displaystyle operatorname {atan2}}$ kann gemäß der folgenden Identität zu einer einzigen Operation zusammengefasst werden

{ displaystyle operatorname {atan2} (y_ {1}, x_ {1}) pm operatorname {atan2} (y_ {2}, x_ {2}) = operatorname {atan2} (y_ {1} x_ { 2} pm y_ {2} x_ {1}, x_ {1} x_ {2} mp y_ {1} y_ {2})}

…unter der Vorraussetzung, dass

{ displaystyle operatorname {atan2} (y_ {1}, x_ {1}) pm operatorname {atan2} (y_ {2}, x_ {2}) in (- pi, pi]}

${ displaystyle operatorname {atan2} (y_ {1}, x_ {1}) pm operatorname {atan2} (y_ {2}, x_ {2}) in (- pi, pi]}$ .

Der Beweis beinhaltet die Betrachtung von zwei Fällen, von denen einer

{ displaystyle y_ {2} neq 0}

${ displaystyle y_ {2} neq 0}$ oder

{ displaystyle x_ {2}> 0}

${ displaystyle x_ {2}> 0}”/></span> und einer wo <span class=$

{ displaystyle y_ {2} = 0}

${ displaystyle y_ {2} = 0}$ und

{ displaystyle x_ {2} <0}

$x_2 < 0$ .

Wir betrachten nur den Fall, in dem

{ displaystyle y_ {2} neq 0}

${ displaystyle y_ {2} neq 0}$ oder

{ displaystyle x_ {2}> 0}

${ displaystyle x_ {2}> 0}”/></span>. Zu Beginn machen wir folgende Beobachtungen: </p> <ol> <li><span class=$
${ displaystyle – operatorname {atan2} (y, x) = operatorname {atan2} (-y, x)}$

${ displaystyle - operatorname {atan2} (y, x) = operatorname {atan2} (-y, x)}$ unter der Vorraussetzung, dass

{ displaystyle y neq 0}

$y neq 0$ oder

{ displaystyle x> 0}

$x> 0″/></span>.</li> <li><span class=$
${ displaystyle operatorname {Arg} (x + iy) = operatorname {atan2} (y, x)}$

${ displaystyle operatorname {Arg} (x + iy) = operatorname {atan2} (y, x)}$ , wo

{ displaystyle operatorname {Arg}}

${ displaystyle operatorname {Arg}}$ ist die komplexe Argumentfunktion.

{ displaystyle theta = operatorname {Arg} e ^ {i theta}}

{ displaystyle operatorname {Arg} (e ^ {i operatorname {Arg} zeta _ {1}} e ^ {i operatorname {Arg} zeta _ {2}}) = operatorname {Arg} ( zeta _ {1} zeta _ {2})}

Um (4) zu sehen, haben wir die Identität

{ displaystyle e ^ {i operatorname {Arg} zeta} = { bar { zeta}}}

${ displaystyle e ^ {i operatorname {Arg} zeta} = { bar { zeta}}}$ wo

{ displaystyle { bar { zeta}} = zeta / left | zeta right |}

${ displaystyle { bar { zeta}} = zeta / left | zeta right |}$ daher

{ displaystyle operatorname {Arg} (e ^ {i operatorname {Arg} zeta _ {1}} e ^ {i operatorname {Arg} zeta _ {2}}) = operatorname {Arg} ({ bar { zeta _ {1}}} { bar { zeta _ {2}}})}

${ displaystyle operatorname {Arg} (e ^ {i operatorname {Arg} zeta _ {1}} e ^ {i operatorname {Arg} zeta _ {2}}) = operatorname {Arg} ({ bar { zeta _ {1}}} { bar { zeta _ {2}}})}$ . Darüber hinaus seit

{ displaystyle operatorname {Arg} zeta = operatorname {Arg} a zeta}

${ displaystyle operatorname {Arg} zeta = operatorname {Arg} a zeta}$ für jeden positiven realen Wert

{ displaystyle a}

$ein$ , wenn wir dann lassen

{ displaystyle zeta = zeta _ {1} zeta _ {2}}

${ displaystyle zeta = zeta _ {1} zeta _ {2}}$ und

{ displaystyle a = { frac {1} { left | zeta _ {1} right | left | zeta _ {2} right |}}}

${ displaystyle a = { frac {1} { left | zeta _ {1} right | left | zeta _ {2} right |}}}$ dann haben wir

{ displaystyle operatorname {Arg} ({ bar { zeta _ {1}}} { bar { zeta _ {2}}}) = operatorname {Arg} ( zeta _ {1} zeta _ {2})}

${ displaystyle operatorname {Arg} ({ bar { zeta _ {1}}} { bar { zeta _ {2}}}) = operatorname {Arg} ( zeta _ {1} zeta _ {2})}$ .

Aus diesen Beobachtungen ergeben sich folgende Äquivalenzen:

{ displaystyle { begin {align} operatorname {atan2} (y_ {1}, x_ {1}) pm operatorname {atan2} (y_ {2}, x_ {2}) & {} = operatorname { atan2} (y_ {1}, x_ {1}) + operatorname {atan2} ( pm y_ {2}, x_ {2}) & { text {by (1)}} \ & {} = Operatorname {Arg} (x_ {1} + iy_ {1}) + Operatorname {Arg} (x_ {2} pm iy_ {2}) & { text {by (2)}} \ & {} = operatorname {Arg} e ^ {i ( operatorname {Arg} (x_ {1} + iy_ {1}) + operatorname {Arg} (x_ {2} pm iy_ {2})} & { text {by (3)}} \ & {} = operatorname {Arg} (e ^ {i operatorname {Arg} (x_ {1} + iy_ {1})} e ^ {i operatorname {Arg} ( x_ {2} pm iy_ {2})}) \ & {} = operatorname {Arg} ((x_ {1} + iy_ {1}) (x_ {2} pm iy_ {2})) & { text {by (4)}} \ & {} = operatorname {Arg} (x_ {1} x_ {2} mp y_ {1} y_ {2} + i (y_ {1} x_ {2 } pm y_ {2} x_ {1})) \ & {} = operatorname {atan2} (y_ {1} x_ {2} pm y_ {2} x_ {1}, x_ {1} x_ { 2} mp y_ {1} y_ {2}) & { text {by (2)}} end {align}}}

Logische Folge: wenn

{ displaystyle (y_ {1}, x_ {1})}

${ displaystyle (y_ {1}, x_ {1})}$ und

{ displaystyle (y_ {2}, x_ {2})}

${ displaystyle (y_ {2}, x_ {2})}$ Bei zweidimensionalen Vektoren wird die Differenzformel in der Praxis häufig verwendet, um den Winkel zwischen diesen Vektoren mit Hilfe von zu berechnen

{ displaystyle operatorname {atan2}}

${ displaystyle operatorname {atan2}}$ , da sich die resultierende Berechnung im Bereich gutartig verhält

{ displaystyle (- pi, pi]}

${ displaystyle (- pi, pi]}$ und kann somit in vielen praktischen Situationen ohne Bereichsprüfung verwendet werden.

Realisierungen der Funktion in gängigen Computersprachen[edit]

Die Realisierung der Funktion unterscheidet sich von Computersprache zu Computersprache:

Die C-Funktion atan2und die meisten anderen Computerimplementierungen wurden entwickelt, um den Aufwand für die Umwandlung von kartesischen in Polarkoordinaten zu verringern und so immer zu definieren atan2(0, 0). Bei Implementierungen ohne vorzeichenbehaftete Null oder wenn positive Nullargumente angegeben werden, wird diese normalerweise als 0 definiert. Es wird immer ein Wert im Bereich zurückgegeben $[-π, π]$ anstatt einen Fehler auszulösen oder eine NaN (keine Zahl) zurückzugeben.

In Common Lisp, wo optionale Argumente vorhanden sind, wird die atan Funktion ermöglicht es einem, optional die zu liefern x Koordinate: (atan y x).^[5]
In Mathematica die Form ArcTan[x, y] wird verwendet, wenn die Ein-Parameter-Form den normalen Arkustangens liefert (beachten Sie, dass die Reihenfolge der Argumente relativ zu der in der obigen Diskussion verwendeten Konvention umgekehrt ist). Mathematica klassifiziert ArcTan[0, 0] als unbestimmter Ausdruck.
In Microsoft Excel^[6]OpenOffice.org Calc, LibreOffice Calc,^[7]Google Spreadsheets,^[8]iWork-Nummern,^[9] und ANSI SQL: 2008 Standard,^[10] das atan2 Bei der Funktion sind die beiden Argumente umgekehrt.
Im Intel Architecture Assembler-Code atan2 ist bekannt als die FPATAN Anweisung (Gleitkomma-Teil-Arkustangens).^[11] Es kann mit Unendlichkeiten umgehen und die Ergebnisse liegen im geschlossenen Intervall $[-π, π]$ , z.B atan2(∞, x) = + $π$ / 2 für endlich x. Insbesondere, FPATAN wird definiert, wenn beide Argumente Null sind:

atan2(+0, +0) = +0;

atan2(+0, −0) = + $π$ ;;

atan2(−0, +0) = –0;

atan2(−0, −0) = – $π$ .

Diese Definition bezieht sich auf das Konzept der vorzeichenbehafteten Null.

Bei den meisten TI-Grafikrechnern (mit Ausnahme von TI-85 und TI-86) wird die entsprechende Funktion aufgerufen R►Pθ und hat die Argumente umgekehrt.
Auf dem TI-85 der $arg$ Funktion wird aufgerufen angle(x,y) und obwohl es zwei Argumente zu nehmen scheint, hat es wirklich nur ein komplexes Argument, das durch ein Zahlenpaar bezeichnet wird: $x + y i = (x, y)$ .
In anderen mathematischen Schriften als dem Quellcode, wie in Büchern und Artikeln, die Notationen Arctan^[12] und Bräunen⁻¹^[13] wurden genutzt; Dies sind großgeschriebene Varianten des regulären Arctan und Tan⁻¹. Diese Verwendung stimmt mit der komplexen Argumentnotation überein, so dass $Eine Lohe(y, x) = Arg (x + y ich)$ .
Behandeln Sie auf HP-Taschenrechnern die Koordinaten als komplexe Zahl und nehmen Sie dann die ARG. Oder << C->R ARG >> 'ATAN2' STO.
Auf wissenschaftlichen Taschenrechnern kann die Funktion oft als der Winkel berechnet werden, der angegeben wird, wenn $((x, y)$ wird von rechteckigen Koordinaten in Polarkoordinaten umgewandelt.
Systeme, die symbolische Mathematik unterstützen, geben normalerweise einen undefinierten Wert für zurück $atan2 (0, 0)$ oder auf andere Weise signalisieren, dass ein abnormaler Zustand aufgetreten ist.
Bei Systemen, die vorzeichenbehaftete Nullen, Unendlichkeiten oder keine Zahl implementieren (z. B. IEEE-Gleitkomma), ist es üblich, angemessene Erweiterungen zu implementieren, die den erzeugten Wertebereich um Folgendes erweitern können: $π$ und –0. Diese können auch NaN zurückgeben oder eine Ausnahme auslösen, wenn ein NaN-Argument angegeben wird.
Für Systeme, die eine vorzeichenbehaftete Null implementieren (z. B. IEEE-Gleitkomma), $atan2 (-0, x)$ , $x$ <0 birgt das Risiko der Rückgabe des Wertes - $π$ , in dem Fall, in dem die Umsetzung von $atan2 (y, x)$ -0 Eingaben werden nicht richtig verarbeitet.
Die kostenlose Mathematikbibliothek FDLIBM (Freely Distributable LIBM) von netlib enthält Quellcode, der zeigt, wie sie implementiert wird atan2 einschließlich der Behandlung der verschiedenen IEEE-Ausnahmewerte.
Für Systeme ohne Hardware-Multiplikator die Funktion $atan2$ kann durch die CORDIC-Methode numerisch zuverlässig implementiert werden. Also Implementierungen von $eine Lohe(y)$ wird wahrscheinlich wählen, um zu berechnen $atan2 (y, 1)$ .

Siehe auch[edit]

Verweise[edit]

^ http://scipp.ucsc.edu/~haber/ph116A/arg_11.pdf
^ Organick, Elliott I. (1966). Ein FORTRAN IV Primer. Addison-Wesley. p. 42. Einige Prozessoren bieten auch die Bibliotheksfunktion ATAN2 an, eine Funktion mit zwei Argumenten (gegenüberliegend und nebeneinander).
^ “src / math / atan2.go”. Die Go-Programmiersprache. Abgerufen 20. April 2018.
^ “Wolf Jung: Mandel, Software für komplexe Dynamik”. www.mndynamics.com. Abgerufen 20. April 2018.
^ “CLHS: Funktion ASIN, ACOS, ATAN”. LispWorks.
^ “Microsoft Excel Atan2-Methode”. Microsoft.
^ “LibreOffice Calc ATAN2”. Libreoffice.org.
^ “Funktionsliste von Google Spreadsheets”.
^ “Trigonometrische Funktionsliste der Zahlen”. Apfel.
^ “ANSI SQL: Standard 2008”. Teradata. Archiviert von das Original am 20.08.2015.
^ IA-32 Intel Architecture Software Entwicklerhandbuch. Band 2A: Instruction Set Reference, AM, 2004.
^ Burger, Wilhelm; Burge, Mark J. (7. Juli 2010). Prinzipien der digitalen Bildverarbeitung: Grundtechniken. Springer Science & Business Media. ISBN 9781848001916. Abgerufen 20. April 2018 – über Google Books.
^ Glisson, Tildon H. (18. Februar 2011). Einführung in die Schaltungsanalyse und das Schaltungsdesign. Springer Science & Business Media. ISBN 9789048194438. Abgerufen 20. April 2018 – über Google Books.

Externe Links[edit]

Andere Implementierungen / Code für atan2

^ Damit

${ displaystyle { text {undefined}} cdot 0 = 0,}$

${ displaystyle { text {undefined}} cdot 1 = { text {undefined}}}$

${ displaystyle z + { text {undefined}} = { text {undefined}}}$
^ Man kann die Periodizität des Ergebnisses anwenden, um es auf einen anderen gewünschten Bereich abzubilden, z $[02π)[02π)$ beim Hinzufügen $2π$ zu den negativen Ergebnissen.

after-content-x4

atan2 – Wikipedia

Geschichte und Motivation[edit]

Definition und Berechnung[edit]

Derivat[edit]

Abbildungen[edit]

Winkelsumme und Differenzidentität[edit]

Realisierungen der Funktion in gängigen Computersprachen[edit]

Siehe auch[edit]

Verweise[edit]

Externe Links[edit]

Recent Posts

Recent Comments

Archives

Categories

Meta