24 Zellen – Wikipedia
| 24 Zellen | |
|---|---|
 |
|
| Art | Konvexes reguläres 4-Polytop |
| Schläfli-Symbol | {3,4,3} r {3,3,4} = {31,1,1} = |
| Coxeter-Diagramm | |
| Zellen | 24 {3,4} |
| Gesichter | 96 {3} |
| Kanten | 96 |
| Eckpunkte | 24 |
| Scheitelpunktfigur | Würfel |
| Petrie Polygon | Zwölfeck |
| Coxeter-Gruppe | F.4, [3,4,3], Bestellung 1152 B.4, [4,3,3], Bestellung 384 D.4, [31,1,1], Bestellung 192 |
| Dual | Self-Dual |
| Eigenschaften | konvex, isogonal, isotoxal, isohedrisch |
| Einheitlicher Index | 22 |
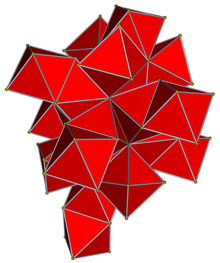
In der vierdimensionalen Geometrie ist die 24 Zellen ist das konvexe reguläre 4-Polytop mit dem Schläfli-Symbol {3,4,3}. Es wird auch genannt C.24, oder der icositetrachoron,Octaplex (kurz für “oktaedrischer Komplex”), icosatetrahedroid,Octacube, Hyper-Diamant oder Polyoktaeder, aus oktaedrischen Zellen aufgebaut.
Die Grenze der 24-Zellen besteht aus 24 oktaedrischen Zellen, wobei sich sechs an jedem Scheitelpunkt und drei an jeder Kante treffen. Zusammen haben sie 96 dreieckige Flächen, 96 Kanten und 24 Eckpunkte. Die Scheitelpunktfigur ist ein Würfel. Die 24-Zellen sind Self-Dual.[a] Es und der Tesserakt sind die einzigen konvexen regulären 4-Polytope, bei denen die Kantenlänge dem Radius entspricht.[b]
Die 24-Zellen haben kein reguläres Analogon in 3 Dimensionen. Es ist das einzige der sechs konvexen regulären 4-Polytope, das nicht das vierdimensionale Analogon eines der fünf regulären platonischen Körper ist. Es kann jedoch als Analogon eines Paares unregelmäßiger Körper angesehen werden: des Kuboktaeders und seines dualen rhombischen Dodekaeders.
Übersetzte Kopien des 24-Zellen-Raums können den vierdimensionalen Raum von Angesicht zu Angesicht kacheln und so die 24-Zellen-Wabe bilden. Als Polytop, das durch Translation gekachelt werden kann, ist die 24-Zelle ein Beispiel für ein Parallelotop, das einfachste, das nicht auch ein Zonotop ist.
Geometrie[edit]
Die 24-Zellen enthalten die Geometrien jedes konvexen regulären Polytops in den ersten vier Dimensionen, mit Ausnahme der 5-Zellen und derjenigen mit einer 5 oder höher in ihrem Schlӓfli-Symbol.[c] Es ist besonders nützlich, die 24-Zellen zu untersuchen, da man die geometrischen Beziehungen zwischen all diesen regulären Polytopen in einer einzelnen 24-Zellen oder ihrer Wabe sehen kann.
Die 24-Zellen sind die vierten in der Folge von 6 konvexen regulären 4-Polytopen (in der Reihenfolge ihrer Größe und Komplexität).[d] Es kann in 3 überlappende Instanzen seines Vorgängers, des Tesseract (8-Zellen), dekonstruiert werden, da die 8-Zellen in 2 überlappende Instanzen seines Vorgängers, der 16-Zellen, dekonstruiert werden können. Das umgekehrte Verfahren zum Konstruieren jeder dieser Instanzen aus einer Instanz ihres Vorgängers behält den Radius des Vorgängers bei, erzeugt jedoch im Allgemeinen einen Nachfolger mit einer anderen Kantenlänge.[e]
Koordinaten[edit]
Quadrate[edit]
Die 24-Zelle ist die konvexe Hülle ihrer Eckpunkte, die als die 24-Koordinaten-Permutationen von:
- .
Diese Koordinaten können wie folgt konstruiert werden ![]()
![]()
![]()
![]()
![]()
![]()
![]() , Berichtigung der 16-Zellen,
, Berichtigung der 16-Zellen, ![]()
![]()
![]()
![]()
![]()
![]()
![]() mit 8 Eckpunkten Permutationen von (± 2,0,0,0). Die Scheitelpunktfigur einer 16-Zelle ist das Oktaeder; Das Schneiden der Eckpunkte der 16-Zellen am Mittelpunkt ihrer einfallenden Kanten erzeugt somit 8 oktaedrische Zellen. Dieser Prozess korrigiert auch die tetraedrischen Zellen der 16-Zellen, die zu 16-Oktaedern werden, wodurch die 24-Zellen-24-Oktaeder-Zellen erhalten werden.
mit 8 Eckpunkten Permutationen von (± 2,0,0,0). Die Scheitelpunktfigur einer 16-Zelle ist das Oktaeder; Das Schneiden der Eckpunkte der 16-Zellen am Mittelpunkt ihrer einfallenden Kanten erzeugt somit 8 oktaedrische Zellen. Dieser Prozess korrigiert auch die tetraedrischen Zellen der 16-Zellen, die zu 16-Oktaedern werden, wodurch die 24-Zellen-24-Oktaeder-Zellen erhalten werden.
In dieser Form hat die 24-Zelle Längenkanten √2 und ist in eine 3-Kugel mit Radius eingeschrieben √2. Bemerkenswerterweise entspricht die Kantenlänge dem Umfang, wie im Sechseck oder im Kuboktaeder. Solche Polytope sind radial gleichseitig.[b]
Die 24 Eckpunkte können als Eckpunkte von 6 orthogonal angesehen werden[f] äquatoriale Quadrate[g] die sich schneiden[h] nur in ihrem gemeinsamen Zentrum.
Sechsecke[edit]

* 1 Ordnung-1: 1 * 1 Ordnung-2: -1 * 6 Ordnung-4: ± i, ± j, ± k * 8 Ordnung-6: (+ 1 ± i ± j ± k) / 2 * 8 Ordnung -3: (-1 ± i ± j ± k) / 2.
Die 24-Zellen sind selbst-dual und haben die gleiche Anzahl von Eckpunkten (24) wie Zellen und die gleiche Anzahl von Kanten (96) wie Flächen.
Ist das Dual der oben genannten 24-Zellen der Kantenlänge √2 wird genommen, indem man es über seine hin- und herbewegt bezeichnet Kugel wird eine weitere 24-Zelle gefunden, die Kantenlänge und Umfang 1 hat und deren Koordinaten mehr Struktur zeigen. In dieser Form können die Eckpunkte der 24-Zellen wie folgt angegeben werden:
8 Eckpunkte erhalten durch Permutieren der ganze Zahl Koordinaten:
- (± 1, 0, 0, 0)
und 16 Eckpunkte mit halbe ganze Zahl Koordinaten des Formulars:
- (±1/.2±1/.2±1/.2±1/.2)
Alle 24 liegen im Abstand 1 vom Ursprung.
Als Quaternionen betrachtet, sind dies die Einheit Hurwitz Quaternionen.
Die 24-Zellen haben einen Einheitsradius und eine Einheitskantenlänge[b] in diesem Koordinatensystem. Wir bezeichnen das System als Einheitsradiuskoordinaten um es von anderen zu unterscheiden, wie dem √2 oben verwendete Radiuskoordinaten.[i]
Die 24 Eckpunkte können als Eckpunkte von 4 orthogonalen äquatorialen Sechsecken angesehen werden[j] die sich schneiden[h] nur in ihrem gemeinsamen Zentrum.[k]
Dreiecke[edit]
Die 24 Eckpunkte können als Eckpunkte von 8 liegenden gleichseitigen Dreiecken angesehen werden[l] in 4 orthogonalen Äquatorialebenen[m] die sich nur in ihrem gemeinsamen Zentrum schneiden.
Hyperkubische Akkorde[edit]
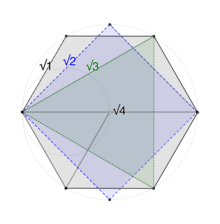
Die 24 Eckpunkte der 24-Zellen sind verteilt[8] bei vier verschiedenen Akkordlängen voneinander: √1, √2, √3 und √4.
Jeder Scheitelpunkt ist mit 8 anderen verbunden[n] durch eine Kante der Länge 1, die 60 ° überspannt = π/.3 des Bogens. Am nächsten sind 6 Eckpunkte[o] befindet sich 90 ° = π/.2 weg, entlang eines inneren Akkords von Länge √2. Weitere 8 Eckpunkte liegen bei 120 ° = 2π/.3 weg, entlang eines inneren Akkords von Länge √3. Der entgegengesetzte Scheitelpunkt ist 180 ° = π entlang eines Durchmessers der Länge 2 entfernt. Schließlich kann, da die 24-Zelle radial gleichseitig ist, ihr Zentrum behandelt werden[p] als 25. kanonischer Scheitelpunkt,[q] Das ist 1 Kantenlänge von allen anderen entfernt.
Beachten Sie die vier Akkordlängen (wie unten beschrieben), um zu veranschaulichen, wie die inneren Polytope der 24-Zellen zusammenpassen (wie unten beschrieben).√1, √2, √3, √4) sind die langen Durchmesser der Hyperwürfel der Dimensionen 1 bis 4: der lange Durchmesser des Quadrats ist √2;; Der lange Durchmesser des Würfels ist √3;; und der lange Durchmesser des Tesserakts ist √4.[r] Darüber hinaus beträgt der lange Durchmesser des Oktaeders √2 wie das Quadrat; und der lange Durchmesser der 24-Zelle selbst ist √4 wie der Tesseract.
Geodäten[edit]
Die Scheitelpunktakkorde der 24-Zellen sind in geodätischen Großkreisen angeordnet, die in Sätzen orthogonaler Ebenen liegen. Der geodätische Abstand zwischen zwei 24-Zellen-Eckpunkten entlang eines Pfades von √1 Kanten ist immer 1, 2 oder 3, und es ist 3 nur für entgegengesetzte Eckpunkte.[s]
Das √1 Kanten treten in 16 hexagonalen Großkreisen auf (4 Sätze von 4 orthogonalen[k] Ebenen), von denen sich 4 an jedem Scheitelpunkt kreuzen.[u] Die 96 unterscheiden sich √1 Kanten teilen die Oberfläche in 96 dreieckige Flächen und 24 oktaedrische Zellen: eine 24-Zellen.
Das √2 Akkorde treten in 18 quadratischen Großkreisen auf (3 Sätze von 6 orthogonal[f] Ebenen), von denen sich 3 an jedem Scheitelpunkt kreuzen.[v] Die 72 unterscheiden sich √2 Akkorde laufen nicht in den gleichen Ebenen wie die sechseckigen Großkreise; Sie folgen nicht den Rändern der 24 Zellen, sondern durchlaufen ihre Zellzentren unterhalb einer ihrer Mittelkanten.[w]
Das √3 Akkorde treten in 32 dreieckigen Großkreisen in 16 Ebenen (4 Sätze von 4 orthogonalen Ebenen) auf, von denen sich 4 an jedem Scheitelpunkt kreuzen.[x] Die 96 unterscheiden sich √3 Akkorde verlaufen von Scheitelpunkt zu Scheitelpunkt in den gleichen Ebenen wie die sechseckigen Großkreise.[l]
Das √4 Akkorde treten als 12 Scheitelpunkt-zu-Scheitelpunkt-Durchmesser (3 Sätze mit 4 orthogonalen Achsen) auf, die 24 Radien um den 25. zentralen Scheitelpunkt.[q]
Das √1 Kanten treten in 48 parallelen Paaren auf, √3 ein Teil. Das √2 Akkorde kommen in 36 parallelen Paaren vor, √2 ein Teil. Das √3 Akkorde kommen in 48 parallelen Paaren vor, √1 ein Teil.[y]
Jede Großkreisebene schneidet sich[h] mit jeder der anderen Großkreisebenen oder Flächenebenen, zu denen es nur im Mittelpunkt orthogonal ist, und mit jeder der anderen, zu denen es an keiner einzelnen Kante orthogonal ist. In jedem Fall ist diese Kante einer der Scheitelpunktakkorde der 24-Zellen.[aa]
Konstruktionen[edit]
Dreiecke und Quadrate kommen in der 24-Zellen-Zelle auf einzigartige Weise zusammen, um als innere Merkmale Folgendes zu erzeugen:[p] Alle regelmäßigen konvexen Polytope mit Dreiecks- und Quadratgesicht in den ersten vier Dimensionen (mit Einschränkungen für die 5-Zellen- und die 600-Zellen-Zelle).[ab] Folglich gibt es zahlreiche Möglichkeiten, die 24-Zellen zu konstruieren oder zu dekonstruieren.
Reziproke Konstruktionen aus 8-Zellen und 16-Zellen[edit]
Die 8 ganzzahligen Scheitelpunkte (± 1, 0, 0, 0) sind die Scheitelpunkte einer regulären 16-Zellen- und die 16 halb ganzzahligen Scheitelpunkte (±)1/.2±1/.2±1/.2±1/.2) sind die Eckpunkte seines Dualen, des Tesseracts (8 Zellen). Der Tesseract gibt Gossets Konstruktion der 24-Zellen, was dem Schneiden eines Tesseracts in 8 kubische Pyramiden und dem anschließenden Anbringen an den Facetten eines zweiten Tesseracts entspricht. Die analoge Konstruktion im 3-Raum ergibt das rhombische Dodekaeder, das jedoch nicht regelmäßig ist. Die 16-Zellen geben die wechselseitige Konstruktion der 24-Zellen-Konstruktion von Cesaro an, die der Gleichrichtung einer 16-Zellen entspricht (Abschneiden ihrer Ecken an den Mittelkanten, wie oben beschrieben). Die analoge Konstruktion im 3-Raum ergibt das Kuboktaeder (Dual des rhombischen Dodekaeders), das jedoch nicht regelmäßig ist. Der Tesseract und die 16-Zellen sind die einzigen regulären 4-Polytope in den 24-Zellen.[13]
Wir können die 16 Eckpunkte mit ganzzahligen Zahlen weiter in zwei Gruppen unterteilen: diejenigen, deren Koordinaten eine gerade Anzahl von Minuszeichen (-) enthalten, und diejenigen mit einer ungeraden Anzahl. Jede dieser Gruppen von 8 Eckpunkten definiert auch eine reguläre 16-Zellen. Dies zeigt, dass die Eckpunkte der 24-Zellen in drei disjunkte Achtergruppen gruppiert werden können, wobei jede Gruppe eine reguläre 16-Zelle definiert und das Komplement den dualen Tesserakt definiert.EIN_und_Abb_8.2B._42-0 “class =” reference “> A._und_Abb_8.2B.-42 “>[14] Dies zeigt auch, dass die Symmetrien der 16-Zellen eine Untergruppe des Index 3 der Symmetriegruppe der 24-Zellen bilden.
Verminderungen[edit]
Wir können die 24-Zellen durch Schneiden abschneiden[ac] durch innere Zellen, die durch Scheitelpunktakkorde begrenzt sind, um Scheitelpunkte zu entfernen, wodurch die Facetten der inneren 4-Polytope freigelegt werden, die in die 24-Zellen eingeschrieben sind. Man kann eine 24-Zellen-Zelle durch jedes planare Sechseck mit 6 Eckpunkten, jedes planare Rechteck mit 4 Eckpunkten oder jedes Dreieck mit 3 Eckpunkten in zwei Teile schneiden. Die Großkreisebenen (oben) sind nur einige dieser Ebenen. Hier werden wir einige der anderen aufdecken: die Gesichtsebenen[ad] von inneren Polytopen, die die 24-Zellen in zwei ungleiche Teile teilen.[ae]
8 Zellen[edit]
Entfernen Sie ausgehend von einer vollständigen 24-Zellen-Zelle 8 orthogonale Eckpunkte (4 gegenüberliegende Paare auf 4 senkrechten Achsen) und die 8 Kanten, die von jeder ausstrahlen, indem Sie 8 kubische Zellen durchschneiden, die durch begrenzt sind √1 Kanten zum Entfernen von 8 kubischen Pyramiden, deren Scheitelpunkte die zu entfernenden Eckpunkte sind. Dadurch werden 4 Kanten von jedem sechseckigen Großkreis entfernt (wobei nur ein gegenüberliegendes Kantenpaar erhalten bleibt), sodass keine durchgehenden sechseckigen Großkreise übrig bleiben. Jetzt treffen sich 3 senkrechte Kanten und bilden die Ecke eines Würfels an jedem der 16 verbleibenden Eckpunkte.[af] und die 32 verbleibenden Kanten teilen die Oberfläche in 24 quadratische Flächen und 8 kubische Zellen: ein Tesserakt. Es gibt drei Möglichkeiten, dies zu tun (wählen Sie einen Satz von 8 orthogonalen Eckpunkten aus 24), sodass drei solcher Tesserakte in die 24-Zellen-Zelle eingeschrieben sind. Sie überlappen sich, aber die meisten ihrer Elementsätze sind nicht zusammenhängend: Sie teilen eine gewisse Scheitelpunktzahl, aber keine Kantenlänge, Fläche oder Zellvolumen. Sie teilen 4-Inhalte, ihren gemeinsamen Kern.[ag]
16 Zellen[edit]
Beginnen Sie mit einer vollständigen 24-Zellen-Zelle und entfernen Sie die 16 Eckpunkte eines Tesserakts (wobei Sie die 8 oben entfernten Eckpunkte beibehalten), indem Sie 16 tetraedrische Zellen durchschneiden, die durch begrenzt sind √2 Akkorde zum Entfernen von 16 tetraedrischen Pyramiden, deren Scheitelpunkte die zu entfernenden Eckpunkte sind. Dies entfernt 12 quadratische Großkreise (wobei nur ein orthogonaler Satz erhalten bleibt) und alle √1 Kanten, belichten √2 Akkorde als neue Kanten. Jetzt kreuzen sich die verbleibenden 6 quadratischen Großkreise senkrecht, 3 an jedem der 8 verbleibenden Eckpunkte.[ah] und ihre 24 Kanten teilen die Oberfläche in 32 dreieckige Flächen und 16 tetraedrische Zellen: eine 16-Zellen. Es gibt drei Möglichkeiten, wie Sie dies tun können (entfernen Sie 1 von 3 Sätzen von Tesseract-Eckpunkten), sodass drei solcher 16-Zellen in die 24-Zellen eingeschrieben sind. Sie überlappen sich, aber die meisten ihrer Elementsätze sind nicht zusammenhängend: Sie teilen keine Scheitelpunktzahl, Kantenlänge oder Flächenfläche, aber sie teilen das Zellvolumen. Sie teilen auch 4-Inhalte, ihren gemeinsamen Kern.[ag]
Tetraedrische Konstruktionen[edit]
Die 24-Zellen können radial aus 96 gleichseitigen Dreiecken mit Kantenlänge aufgebaut werden √1 die sich in der Mitte des Polytops treffen und jeweils zwei Radien und eine Kante beitragen.[b] Sie bilden 96 √1 Tetraeder, die alle den 25. zentralen Scheitelpunkt teilen. Diese bilden 24 oktaedrische Pyramiden (Halb-16-Zellen) mit ihren Spitzen in der Mitte.
Die 24-Zellen können aus 96 gleichseitigen Dreiecken mit Kantenlänge aufgebaut werden √2, wobei sich die drei Eckpunkte jedes Dreiecks um 90 ° befinden = π/.2 voneinander weg. Sie bilden 48 √2 Tetraeder (die Zellen der drei 16-Zellen), zentriert auf den 24 Mittelradien der 24-Zellen.
Beziehungen zwischen inneren Polytopen[edit]
Die 24-Zellen-, drei Tesseracts und drei 16-Zellen sind tief um ihr gemeinsames Zentrum verwoben und schneiden sich in einem gemeinsamen Kern.[ag] Die Tesserakte sind in die 24-Zellen eingeschrieben[ai] so dass ihre Eckpunkte und Kanten äußere Elemente der 24-Zelle sind, aber ihre quadratischen Flächen und kubischen Zellen innerhalb der 24-Zelle liegen (sie sind keine Elemente der 24-Zelle). Die 16 Zellen sind in die 24 Zellen eingeschrieben[aj] so dass nur ihre Eckpunkte äußere Elemente der 24-Zelle sind: ihre Kanten, dreieckigen Flächen und tetraedrischen Zellen liegen innerhalb der 24-Zelle. Der Innenraum[ak] 16-Zellen-Kanten haben Länge √2.

Die 16-Zellen sind auch in die Tesserakte eingeschrieben: ihre √2 Kanten sind die Gesichtsdiagonalen des Tesserakts, und ihre 8 Eckpunkte belegen jeden zweiten Scheitelpunkt des Tesserakts. In jedem Tesserakt sind zwei 16-Zellen eingeschrieben (die die gegenüberliegenden Eckpunkte und Gesichtsdiagonalen einnehmen), sodass jede 16-Zelle in zwei der drei 8-Zellen eingeschrieben ist. Dies erinnert an die Art und Weise, wie in drei Dimensionen zwei Tetraeder in einen Würfel eingeschrieben werden können, wie Kepler entdeckt hat. Tatsächlich ist es die exakte dimensionale Analogie (die Demihyperwürfel), und die 48 tetraedrischen Zellen sind auf genau diese Weise in die 24 kubischen Zellen eingeschrieben.
Die 24-Zellen-Zelle umschließt die drei Tesserakte in ihrer Hülle aus oktaedrischen Facetten und lässt an einigen Stellen einen vierdimensionalen Raum zwischen ihrer Hülle und der Würfelhülle jedes Tesserakts. Jeder Tesserakt umschließt zwei der drei 16-Zellen und lässt an einigen Stellen einen 4-dimensionalen Raum zwischen seiner Hülle und der Tetraederhülle jeder 16-Zelle. Somit gibt es messbare 4-dimensionale Zwischenräume[al] zwischen den 24-Zellen-, 8-Zellen- und 16-Zellen-Umschlägen. Die Formen, die diese Lücken füllen, sind 4-Pyramiden,[am] oben erwähnt.
Grenzzellen[edit]
Trotz der 4-dimensionalen Zwischenräume zwischen 24-Zellen-, 8-Zellen- und 16-Zellen-Hüllkurven überlappen sich ihre 3-dimensionalen Volumina. Die verschiedenen Umschläge sind an einigen Stellen getrennt und an anderen Stellen in Kontakt (wo keine 4-Pyramide zwischen ihnen liegt). Wo sie in Kontakt stehen, verschmelzen sie und teilen das Zellvolumen: Sie sind an diesen Stellen dieselbe 3-Membran, nicht zwei getrennte, sondern benachbarte dreidimensionale Schichten. Da es insgesamt 7 Umschläge gibt, gibt es Orte, an denen mehrere Umschläge zusammenkommen und das Volumen zusammenführen, sowie Orte, an denen sich Umschläge gegenseitig durchdringen (von innen nach außen kreuzen).
Einige innere Merkmale liegen im 3-Raum der (äußeren) Grenzhülle der 24-Zelle selbst: Jede oktaedrische Zelle wird durch drei senkrechte Quadrate (eines von jedem der Tesserakte) und die Diagonalen dieser Quadrate (die sich kreuzen) halbiert einander senkrecht in der Mitte des Oktaeders) sind 16-Zellen-Kanten (eine von jeder 16-Zellen). Jedes Quadrat halbiert ein Oktaeder in zwei quadratische Pyramiden und verbindet zwei benachbarte kubische Zellen eines Tesserakts als gemeinsame Fläche.
Wie wir oben gesehen haben, 16-Zellen √2 Tetraederzellen sind in Tesseract eingeschrieben √1 kubische Zellen, die das gleiche Volumen teilen. 24 Zellen √1 Oktaederzellen überlappen ihr Volumen mit √1 kubische Zellen: Sie werden durch eine quadratische Fläche in zwei quadratische Pyramiden geteilt, deren Spitzen ebenfalls an einem Scheitelpunkt eines Würfels liegen.[ao] Die Oktaeder teilen das Volumen nicht nur mit den Würfeln, sondern auch mit den darin eingeschriebenen Tetraedern; Somit teilen sich die 24-Zellen, Tesserakte und 16-Zellen alle ein gewisses Grenzvolumen.[ap]
Als Konfiguration[edit]
Diese Konfigurationsmatrix repräsentiert die 24 Zellen. Die Zeilen und Spalten entsprechen Eckpunkten, Kanten, Flächen und Zellen. Die diagonalen Zahlen geben an, wie viele Elemente in der gesamten 24-Zellen-Zelle vorkommen. Die nicht diagonalen Zahlen geben an, wie viele Elemente der Spalte im oder am Element der Zeile vorkommen.
Da die 24-Zellen selbst dual sind, ist ihre Matrix identisch mit ihrer 180-Grad-Drehung.
Symmetrien, Wurzelsysteme und Tessellationen[edit]
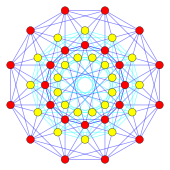
Die 24 Wurzelvektoren des D.4 Das Wurzelsystem der einfachen Lie-Gruppe SO (8) bildet die Eckpunkte einer 24-Zellen. Die Eckpunkte sind in 3 Hyperebenen zu sehen.[aq] mit den 6 Eckpunkten einer Oktaederzelle auf jeder der äußeren Hyperebenen und 12 Eckpunkten eines Kuboktaeders auf einer zentralen Hyperebene. Diese Eckpunkte repräsentieren zusammen mit den 8 Eckpunkten der 16-Zellen die 32 Wurzelvektoren des B.4 und C4 einfache Lügengruppen.
Die 48 Eckpunkte (oder genau genommen ihre Radiusvektoren) der Vereinigung der 24-Zellen und ihrer Dualen bilden das Wurzelsystem vom Typ F.4. Die 24 Eckpunkte der ursprünglichen 24-Zellen bilden ein Wurzelsystem vom Typ D.4;; seine Größe hat das Verhältnis √2: 1. Dies gilt ebenfalls für die 24 Eckpunkte seines Duals. Die vollständige Symmetriegruppe der 24-Zellen ist die Weyl-Gruppe von F.4, die durch Reflexionen durch die zu F orthogonalen Hyperebenen erzeugt wird4 Wurzeln. Dies ist eine lösbare Gruppe der Ordnung 1152. Die Rotationssymmetriegruppe der 24-Zellen liegt in der Ordnung 576.
Quaternionische Interpretation[edit]
Bei der Interpretation als Quaternionen wird das F.4Das Wurzelgitter (das die integrale Spanne der Eckpunkte der 24-Zellen ist) wird unter Multiplikation geschlossen und ist daher ein Ring. Dies ist der Ring der integralen Hurwitz-Quaternionen. Die Eckpunkte der 24-Zellen bilden die Gruppe der Einheiten (dh die Gruppe der invertierbaren Elemente) im Hurwitz-Quaternionsring (diese Gruppe wird auch als binäre tetraedrische Gruppe bezeichnet). Die Eckpunkte der 24-Zellen sind genau die 24 Hurwitz-Quaternionen mit dem Normquadrat 1, und die Eckpunkte der dualen 24-Zellen sind diejenigen mit dem Normquadrat 2. Das D.4 Wurzelgitter ist das Dual des F.4 und wird durch den Subring von Hurwitz-Quaternionen mit gerader Norm im Quadrat gegeben.
Eckpunkte anderer konvexer regulärer 4-Polytope bilden ebenfalls multiplikative Gruppen von Quaternionen, aber nur wenige von ihnen erzeugen ein Wurzelgitter.
Voronoi-Zellen[edit]
Die Voronoi-Zellen des D.4 Wurzelgitter sind reguläre 24-Zellen. Die entsprechende Voronoi-Tessellation ergibt die Tessellation des 4-dimensionalen euklidischen Raums durch reguläre 24-Zellen, die 24-Zellen-Wabe. Die 24 Zellen sind am D zentriert4 Gitterpunkte (Hurwitz-Quaternionen mit gerader Norm im Quadrat), während die Eckpunkte am F liegen4 Gitterpunkte mit ungerader Norm im Quadrat. Jede 24-Zelle dieser Tessellation hat 24 Nachbarn. Mit jedem von diesen teilt es ein Oktaeder. Es hat auch 24 andere Nachbarn, mit denen es nur einen einzigen Scheitelpunkt teilt. Acht 24-Zellen treffen sich an einem bestimmten Scheitelpunkt in dieser Tessellation. Das Schläfli-Symbol für diese Tessellation ist {3,4,3,3}. Es ist eine von nur drei regelmäßigen Tessellationen von R.4.
Die in die 24 Zellen dieser Tessellation eingeschriebenen Einheitskugeln führen zu der dichtesten bekannten Gitterpackung von Hypersphären in 4 Dimensionen. Es wurde auch gezeigt, dass die Scheitelpunktkonfiguration der 24-Zellen die höchstmögliche Kusszahl in 4 Dimensionen ergibt.
Radial gleichseitige Wabe[edit]
Die doppelte Tessellation der 24-zelligen Wabe {3,4,3,3} ist die 16-zellige Wabe {3,3,4,3}. Die dritte reguläre Tessellation des vierdimensionalen Raums ist die tesseraktische Wabe {4,3,3,4}, deren Eckpunkte durch kartesische 4-Ganzzahl-Koordinaten beschrieben werden können. Die kongruenten Beziehungen zwischen diesen drei Tessellationen können bei der Visualisierung der 24-Zellen hilfreich sein, insbesondere der radialen gleichseitigen Symmetrie, die sie mit dem Tesserakt teilt.[b]
Eine Wabe aus 24 Zellen mit Einheitskantenlänge kann einer Wabe aus Tesserakten mit Einheitskantenlänge überlagert werden, so dass jeder Scheitelpunkt eines Tesserakts (jede 4-Ganzzahl-Koordinate) auch der Scheitelpunkt einer 24-Zellen-Einheit (und eines Tesserakts) ist Kanten sind auch Kanten mit 24 Zellen), und jedes Zentrum einer 24-Zellen-Zelle ist auch das Zentrum eines Tesserakts. Die 24-Zellen sind doppelt so groß wie die Tesserakte durch 4-dimensionalen Inhalt (Hypervolumen), so dass es insgesamt zwei Tesserakte für jede 24-Zelle gibt, von denen nur die Hälfte in eine 24-Zelle eingeschrieben ist. Wenn diese Tesserakte schwarz gefärbt sind und ihre benachbarten Tesserakte (mit denen sie eine kubische Facette teilen) rot gefärbt sind, ergibt sich ein 4-dimensionales Schachbrett. Von den 24 Radien von Mitte zu Scheitelpunkt[ar] von jeder 24-Zelle sind 16 auch die Radien eines schwarzen Tesserakts, der in die 24-Zelle eingeschrieben ist. Die anderen 8 Radien erstrecken sich außerhalb des schwarzen Tesserakts (durch die Zentren seiner kubischen Facetten) bis zu den Zentren der 8 benachbarten roten Tesserakte. Somit fallen die 24-Zellen-Wabe und die tesseraktische Wabe auf besondere Weise zusammen: 8 der 24 Eckpunkte jeder 24-Zellen-Welle treten nicht an einem Scheitelpunkt eines Tesserakts auf (sie treten stattdessen in der Mitte eines Tesserakts auf). Jeder schwarze Tesserakt wird aus einer 24-Zellen-Zelle herausgeschnitten, indem er an diesen 8 Eckpunkten abgeschnitten wird und 8 kubische Pyramiden abgeschnitten werden (wie bei der Umkehrung von Gossets Konstruktion, aber anstatt entfernt zu werden, werden die Pyramiden einfach rot gefärbt und an Ort und Stelle belassen). Acht 24-Zellen treffen sich in der Mitte jedes roten Tesserakts: Jede trifft ihr Gegenteil an diesem gemeinsamen Scheitelpunkt und die sechs anderen an einer gemeinsamen oktaedrischen Zelle.
Die roten Tesserakte sind gefüllte Zellen (sie enthalten einen zentralen Scheitelpunkt und Radien); Die schwarzen Tesserakte sind leere Zellen. Der Scheitelpunktsatz dieser Vereinigung zweier Waben enthält die Scheitelpunkte aller 24 Zellen und Tesserakte sowie die Zentren der roten Tesserakte. Das Hinzufügen der 24-Zellen-Zentren (die auch die schwarzen Tesseract-Zentren sind) zu dieser Wabe ergibt eine 16-Zellen-Wabe, deren Scheitelpunktsatz alle Scheitelpunkte und Zentren aller 24-Zellen und Tesseracts enthält. Die ehemals leeren Zentren benachbarter 24-Zellen werden zu entgegengesetzten Eckpunkten einer 16-Zellen-Einheitskantenlänge. 24 Halb-16-Zellen (oktaedrische Pyramiden) treffen sich an jedem ehemals leeren Zentrum, um jede 24-Zelle zu füllen, und ihre oktaedrischen Basen sind die 6-Vertex-Oktaeder-Facetten der 24-Zelle (gemeinsam mit einer benachbarten 24-Zelle).
Rotationen[edit]
Es gibt drei verschiedene Ausrichtungen der tesseraktischen Wabe, die auf diese Weise mit der 24-Zellen-Wabe zusammenfallen könnten, abhängig davon, welcher der drei disjunkten Sätze von 24 Zellen mit 8 orthogonalen Eckpunkten (welcher Satz von 4 senkrechten Achsen) gewählt wurde um es auszurichten, so wie drei Tesserakte in die 24-Zellen eingeschrieben werden können, die gegeneinander gedreht sind. Der Abstand von einer dieser Orientierungen zu einer anderen ist eine isokline Drehung um 60 Grad (eine doppelte Drehung von 60 Grad in jedem Paar orthogonaler Achsenebenen um einen einzelnen Fixpunkt).[at] Diese Drehung ist am deutlichsten in den sechseckigen Mittelebenen zu sehen, in denen sich das Sechseck dreht, um zu ändern, welcher seiner drei Durchmesser mit einer Koordinatensystemachse ausgerichtet ist.[j]
Projektionen[edit]
Parallele Projektionen[edit]

Das Scheitelpunkt zuerst Die parallele Projektion der 24-Zellen in den dreidimensionalen Raum weist eine rhombische dodekaedrische Hülle auf. Zwölf der 24 oktaedrischen Zellen projizieren paarweise auf sechs quadratische Dipyramiden, die sich im Zentrum des rhombischen Dodekaeders treffen. Die verbleibenden 12 oktaedrischen Zellen projizieren auf die 12 rhombischen Flächen des rhombischen Dodekaeders.
Das Zelle zuerst Die parallele Projektion der 24-Zellen in den dreidimensionalen Raum hat eine kuboktaedrische Hülle. Zwei der oktaedrischen Zellen, die dem Betrachter am nächsten und weiter entfernt sind w-Achse, projizieren Sie auf ein Oktaeder, dessen Eckpunkte in der Mitte der quadratischen Flächen des Kuboktaeders liegen. Um dieses zentrale Oktaeder herum liegen die Projektionen von 16 anderen Zellen mit 8 Paaren, die jeweils auf eines der 8 Volumina projizieren, die zwischen einer dreieckigen Fläche des zentralen Oktaeders und der nächsten dreieckigen Fläche des Kuboktaeders liegen. Die verbleibenden 6 Zellen ragen auf die quadratischen Flächen des Kuboktaeders. Dies entspricht der Zerlegung des Kuboktaeders in ein reguläres Oktaeder und 8 unregelmäßige, aber gleiche Oktaeder, von denen jedes die Form der konvexen Hülle eines Würfels hat, wobei zwei gegenüberliegende Eckpunkte entfernt sind.
Das Rand zuerst Parallelprojektion hat eine längliche hexagonale dipyramidale Hülle, und die Gesicht zuerst Die parallele Projektion hat eine ungleichmäßige hexagonale bi-antiprismische Hülle.
Perspektivische Projektionen[edit]
Das Scheitelpunkt zuerst Die perspektivische Projektion der 24-Zellen in den dreidimensionalen Raum hat eine hexaedrische Tetrakis-Hülle. Das Layout der Zellen in diesem Bild ähnelt dem Bild bei paralleler Projektion.
Die folgende Bildsequenz zeigt die Struktur der perspektivischen Projektion der 24 Zellen in drei Dimensionen. Der 4D-Ansichtspunkt befindet sich in einem Abstand von dem Fünffachen des Scheitelpunkt-Radius der 24-Zellen.
| Cell-First-Perspektivprojektion | ||
|---|---|---|
 In diesem Bild wird die nächste Zelle rot dargestellt, und die verbleibenden Zellen befinden sich in Randumrissen. Aus Gründen der Klarheit wurden Zellen, die vom 4D-Standpunkt weg weisen, ausgesondert. |
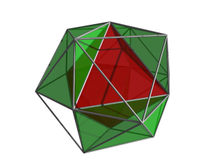 In diesem Bild sind vier der 8 Zellen, die die nächste Zelle umgeben, grün dargestellt. Die vierte Zelle befindet sich unter diesem Gesichtspunkt hinter der zentralen Zelle (leicht erkennbar, da die rote Zelle halbtransparent ist). |
 Schließlich werden alle 8 Zellen angezeigt, die die nächste Zelle umgeben, wobei die letzten vier in Magenta dargestellt sind. |
| Beachten Sie, dass diese Bilder keine Zellen enthalten, die vom 4D-Standpunkt weg zeigen. Daher sind hier nur 9 Zellen gezeigt. Auf der anderen Seite der 24-Zellen befinden sich weitere 9 Zellen in identischer Anordnung. Die verbleibenden 6 Zellen liegen am “Äquator” der 24-Zellen und überbrücken die beiden Zellensätze. | ||
Orthogonale Projektionen[edit]
Visualisierung[edit]
Die 24-Zellen werden von 24 oktaedrischen Zellen begrenzt. Für Visualisierungszwecke ist es zweckmäßig, dass das Oktaeder gegenüberliegende parallele Flächen aufweist (eine Eigenschaft, die es mit den Zellen des Tesseracts und der 120-Zellen teilt). Man kann Oktaeder von Angesicht zu Angesicht in einer geraden Linie stapeln, die in der 4. Richtung zu einem großen Kreis mit einem Umfang von 6 Zellen gebogen ist. Die Zellpositionen eignen sich für eine hypersphärische Beschreibung. Wählen Sie eine beliebige Zelle und bezeichnen Sie sie als “Nordpol”. Acht Großkreismeridiane (zwei Zellen lang) strahlen dreidimensional aus und laufen an der 3. “Südpol” -Zelle zusammen. Dieses Skelett macht 18 der 24 Zellen aus (2 +) 8×2). Siehe die folgende Tabelle.
In der 24-Zellen gibt es einen weiteren verwandten Großkreis, den Dualen des obigen. Ein Pfad, der 6 Eckpunkte ausschließlich entlang der Kanten durchquert, befindet sich im Dual dieses Polytops, das selbst ist, da es selbst dual ist. Dies sind die oben beschriebenen hexagonalen Geodäten. Diesen Weg kann man leicht in einer Darstellung des äquatorialen Kuboktaederquerschnitts verfolgen.
Ausgehend vom Nordpol können wir die 24-Zellen in 5 Breitenschichten aufbauen. Mit Ausnahme der Pole repräsentiert jede Schicht eine separate 2-Kugel, wobei der Äquator eine große 2-Kugel ist. Die in der folgenden Tabelle als äquatorial bezeichneten Zellen sind interstitiell zu den Meridian-Großkreiszellen. Die interstitiellen “äquatorialen” Zellen berühren die Meridianzellen an ihren Gesichtern. Sie berühren sich und die Polzellen an ihren Eckpunkten. Diese letztere Untergruppe von acht Nicht-Meridian- und Polzellen hat dieselbe relative Position zueinander wie die Zellen in einem Tesserakt (8 Zellen), obwohl sie sich an ihren Eckpunkten anstatt an ihren Gesichtern berühren.
| Layer # | Anzahl der Zellen | Beschreibung | Colatitude | Region |
|---|---|---|---|---|
| 1 | 1 Zelle | Nordpol | 0 ° | Nördliche Hemisphäre |
| 2 | 8 Zellen | Erste Schicht von Meridianzellen | 60 ° | |
| 3 | 6 Zellen | Nichtmeridian / Interstitial | 90 ° | Äquator |
| 4 | 8 Zellen | Zweite Schicht von Meridianzellen | 120 ° | Südlichen Hemisphäre |
| 5 | 1 Zelle | Südpol | 180 ° | |
| Gesamt | 24 Zellen | |||

Die 24-Zellen können in disjunkte Sätze von vier dieser 6-Zellen-Großkreisringe unterteilt werden, wodurch eine diskrete Hopf-Fibration von vier ineinandergreifenden Ringen gebildet wird. Ein Ring ist “vertikal” und umfasst die Polzellen und vier Meridianzellen. Die anderen drei Ringe umfassen jeweils zwei Äquatorzellen und vier Meridianzellen, zwei aus der nördlichen Hemisphäre und zwei aus der südlichen.
Beachten Sie, dass dieser Sechskant-Großkreispfad impliziert, dass der Innen- / Diederwinkel zwischen benachbarten Zellen 180 – 360/6 = 120 Grad beträgt. Dies legt nahe, dass Sie nebeneinander genau drei 24-Zellen in einer Ebene stapeln und eine 4-D-Wabe aus 24 Zellen bilden können, wie zuvor beschrieben.
Man kann auch einer Großkreisroute durch die gegenüberliegenden Eckpunkte der Oktaeder folgen, die vier Zellen lang ist. Dies sind die quadratischen Geodäten entlang vier √2 oben beschriebene Akkorde. Dieser Weg entspricht einer diagonalen Durchquerung der Quadrate im Kuboktaederquerschnitt. Die 24-Zellen-Zelle ist das einzige reguläre Polytop in mehr als zwei Dimensionen, bei dem Sie einen Großkreis nur durch gegenüberliegende Eckpunkte (und das Innere) jeder Zelle durchqueren können. Dieser große Kreis ist selbst dual. Dieser Pfad wurde oben in Bezug auf den Satz von 8 Nicht-Meridian- (Äquatorial-) und Polzellen angesprochen. Die 24-Zellen können in drei 8-Zellen-Teilmengen aufgeteilt werden, die jeweils die Organisation eines Tesserakts haben. Jede dieser Untergruppen kann weiter in zwei ineinandergreifende Großkreis-Ketten mit vier Zellen Länge aufgeteilt werden. Zusammen erzeugen diese drei Untergruppen jetzt eine weitere diskrete Hopf-Fibration mit sechs Ringen.
Drei Coxeter-Gruppenkonstruktionen[edit]
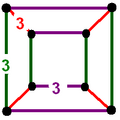
Es gibt zwei Formen mit niedrigerer Symmetrie der 24-Zellen, abgeleitet als gleichgerichtete 16-Zellen, mit B4 oder [3,3,4] Symmetrie zweifarbig gezeichnet mit 8 und 16 oktaedrischen Zellen. Schließlich kann es aus D konstruiert werden4 oder [31,1,1] Symmetrie und dreifarbig mit jeweils 8 Oktaedern gezeichnet.
| Drei Netze der 24 Zellen mit durch D gefärbten Zellen4B.4und F.4 Symmetrie | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Korrigierter Demitesserakt | Korrigierte 16-Zellen | Regelmäßige 24-Zellen | |||||||||
| D.4, [31,1,1], Bestellung 192 | B.4, [3,3,4], Bestellung 384 | F.4, [3,4,3], Bestellung 1152 | |||||||||

|
|||||||||||
| Drei Sätze von 8 gleichgerichteten tetraedrischen Zellen | Ein Satz von 16 gleichgerichteten tetraedrischen Zellen und ein Satz von 8 oktaedrischen Zellen. | Ein Satz von 24 oktaedrischen Zellen | |||||||||
| Scheitelpunktfigur (Jede Kante entspricht einer dreieckigen Fläche, die durch Symmetrieanordnung gefärbt ist.) |
|||||||||||
|

|

|
|||||||||
Verwandte komplexe Polygone[edit]
Das reguläre komplexe Polygon 4{3}4, ![]()
![]()
![]() oder
oder ![]()
![]()
![]() enthält die 24 Eckpunkte der 24-Zellen und 24 4-Kanten, die den zentralen Quadraten von 24 von 48 oktaedrischen Zellen entsprechen. Seine Symmetrie ist 4[3]4, Bestellung 96.
enthält die 24 Eckpunkte der 24-Zellen und 24 4-Kanten, die den zentralen Quadraten von 24 von 48 oktaedrischen Zellen entsprechen. Seine Symmetrie ist 4[3]4, Bestellung 96.
Das reguläre komplexe Polytop 3{4}3, ![]()
![]()
![]() oder
oder ![]()
![]()
![]() , im
, im
hat eine reale Darstellung als 24-Zellen im 4-dimensionalen Raum. 3{4}3 hat 24 Eckpunkte und 24 3-Kanten. Seine Symmetrie ist 3[4]3, Bestellung 72.
| Name | {3,4,3}, |
4{3}4, |
3{4}3, |
|---|---|---|---|
| Symmetrie | [3,4,3], |
4[3]4, |
3[4]3, |
| Eckpunkte | 24 | 24 | 24 |
| Kanten | 96 2-Kanten | 24 4-Rand | 24 3-Kanten |
| Bild |  24 Zellen in der F4-Coxeter-Ebene mit 24 Eckpunkten in zwei Ringen mit 12 und 96 Kanten. |
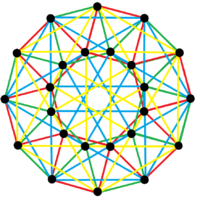 4{3}4, |
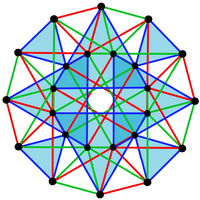 3{4}3 oder |
Verwandte 4-Polytope[edit]
Durch Verkürzung können mehrere einheitliche 4-Polytope aus den 24-Zellen abgeleitet werden:
Die 96 Kanten der 24-Zellen können in den goldenen Schnitt unterteilt werden, um die 96 Eckpunkte der 24-Zellen-Snub zu erzeugen. Dies erfolgt, indem zuerst Vektoren entlang der Kanten der 24 Zellen so platziert werden, dass jede zweidimensionale Fläche durch einen Zyklus begrenzt wird, und dann jede Kante in ähnlicher Weise entlang der Richtung ihres Vektors in den goldenen Schnitt unterteilt wird. Eine analoge Modifikation eines Oktaeders erzeugt ein Ikosaeder oder “Stupsoktaeder”.
Die 24-Zellen-Zelle ist das einzigartige konvexe selbst-duale reguläre euklidische Polytop, das weder ein Polygon noch ein Simplex ist. Die Lockerung des Konvexitätszustands lässt zwei weitere Zahlen zu: die großen 120-Zellen- und die großartigen 120-Zellen-Sternchen. Mit sich selbst kann es eine Polytopverbindung bilden: die Verbindung von zwei 24-Zellen.
Verwandte einheitliche Polytope[edit]
| D.4 einheitliche Polychora | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|

|

|

|

|

|

|

|

|
||||
| {3,31,1}} h {4,3,3} |
2r {3,31,1}} h3{4,3,3} |
t {3,31,1}} h2{4,3,3} |
2t {3,31,1}} h2,3{4,3,3} |
r {3,31,1}} {31,1,1} = {3,4,3} |
rr {3,31,1}} r {31,1,1} = r {3,4,3} |
tr {3,31,1}} t {31,1,1} = t {3,4,3} |
sr {3,31,1}} s {31,1,1} = s {3,4,3} |
||||
| Polytope der 24-Zell-Familie | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Name | 24 Zellen | verkürzte 24-Zellen | Stups 24-Zellen | korrigierte 24-Zellen | Cantellated 24-Zellen | bitruncated 24-cell | cantitruncated 24-cell | runcinierte 24-Zellen | runcitruncated 24-cell | omnitruncated 24-cell | |
| Schläfli Symbol |
{3,4,3} | t0,1{3,4,3} t {3,4,3} |
s {3,4,3} | t1{3,4,3} r {3,4,3} |
t0,2{3,4,3} rr {3,4,3} |
t1,2{3,4,3} 2t {3,4,3} |
t0,1,2{3,4,3} tr {3,4,3} |
t0,3{3,4,3} | t0,1,3{3,4,3} | t0,1,2,3{3,4,3} | |
| Coxeter Diagramm |
|||||||||||
| Schlegel Diagramm |

|

|

|

|

|

|

|

|

|

|
|
| F.4 | 
|

|

|

|

|

|

|

|

|

|
|
| B.4 | 
|

|

|

|

|

|

|

|

|

|
|
| B.3(ein) | 
|

|

|

|

|

|

|

|

|

|
|
| B.3(b) | 
|

|

|

|

|

|
|||||
| B.2 | 
|

|

|

|

|

|

|

|

|

|
|
Die 24-Zellen können auch als gleichgerichtete 16-Zellen abgeleitet werden:
| B4-Symmetriepolytope | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Name | Tesseract | korrigiert Tesseract |
gekürzt Tesseract |
kantelliert Tesseract |
runciniert Tesseract |
bitruncated Tesseract |
cantitruncated Tesseract |
runcitruncated Tesseract |
omnitruncated Tesseract |
||
| Coxeter Diagramm |
= |
= |
|||||||||
| Schläfli Symbol |
{4,3,3} | t1{4,3,3} r {4,3,3} |
t0,1{4,3,3} t {4,3,3} |
t0,2{4,3,3} rr {4,3,3} |
t0,3{4,3,3} | t1,2{4,3,3} 2t {4,3,3} |
t0,1,2{4,3,3} tr {4,3,3} |
t0,1,3{4,3,3} | t0,1,2,3{4,3,3} | ||
| Schlegel Diagramm |

|

|

|

|

|

|

|

|

|
||
| B.4 | 
|

|

|

|

|

|

|

|

|
||
| Name | 16 Zellen | korrigiert 16 Zellen |
gekürzt 16 Zellen |
kantelliert 16 Zellen |
runciniert 16 Zellen |
bitruncated 16 Zellen |
cantitruncated 16 Zellen |
runcitruncated 16 Zellen |
omnitruncated 16 Zellen |
||
| Coxeter Diagramm |
= |
= |
= |
= |
= |
= |
|||||
| Schläfli Symbol |
{3,3,4} | t1{3,3,4} r {3,3,4} |
t0,1{3,3,4} t {3,3,4} |
t0,2{3,3,4} rr {3,3,4} |
t0,3{3,3,4} | t1,2{3,3,4} 2t {3,3,4} |
t0,1,2{3,3,4} tr {3,3,4} |
t0,1,3{3,3,4} | t0,1,2,3{3,3,4} | ||
| Schlegel Diagramm |

|

|

|

|

|

|

|

|

|
||
| B.4 | 
|

|

|

|

|

|

|

|

|
||
| {3,p, 3} Polytope | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Raum | S.3 | H.3 | |||||||||
| Bilden | Endlich | Kompakt | Parakompakt | Nicht kompakt | |||||||
| {3,p,3} | {3,3,3} | {3,4,3} | {3,5,3} | {3,6,3} | {3,7,3} | {3,8,3} | … {3, ∞, 3} | ||||
| Bild | 
|

|

|

|

|

|

|
||||
| Zellen |  {3,3} |
 {3,4} |
 {3,5} |
 {3,6} |
 {3,7} |
 {3,8} |
 {3, ∞} |
||||
| Scheitel Zahl |
 {3,3} |
 {4,3} |
 {5,3} |
 {6,3} |
 {7,3} |
 {8,3} |
 {∞, 3} |
||||
Siehe auch[edit]
- ^ Die 24-Zellen sind eines von nur drei selbst-dualen regulären euklidischen Polytopen, die weder ein Polygon noch ein Simplex sind. Die anderen beiden sind ebenfalls 4-Polytope, aber nicht konvex: die großartigen 120-Zellen und die großen 120-Zellen.
- ^ ein b c d e f G Der lange Radius (Mitte zum Scheitelpunkt) der 24-Zellen entspricht ihrer Kantenlänge. somit beträgt sein langer Durchmesser (Scheitelpunkt zum gegenüberliegenden Scheitelpunkt) 2 Kantenlängen. Nur wenige einheitliche Polytope haben diese Eigenschaft, einschließlich des vierdimensionalen 24-Zellen- und Tesserakts, des dreidimensionalen Kuboktaeders und des zweidimensionalen Sechsecks. (Das Kuboktaeder ist der äquatoriale Querschnitt der 24-Zellen, und das Sechseck ist der äquatoriale Querschnitt des Kuboktaeders.) Radial gleichseitig Polytope sind solche, die mit ihren langen Radien aus gleichseitigen Dreiecken konstruiert werden können, die sich in der Mitte des Polytops treffen und jeweils zwei Radien und eine Kante beitragen.
- ^ Die konvexen regelmäßigen Polytope in den ersten vier Dimensionen mit einer 5 im Schlӓfli-Symbol sind das Fünfeck {5}, das Dodekaeder {5, 3}, das 600-Zellen {3,3,5} und das 120-Zellen {5, 3,3}. Mit anderen Worten, die 24-Zellen besitzen alle der dreieckigen und quadratischen Merkmale, die in vier Dimensionen mit Ausnahme der regulären 5-Zellen existieren, aber keiner der fünfeckigen Merkmale.
- ^ Die konvexen regulären 4-Polytope können nach Größe als Maß für den 4-dimensionalen Gehalt (Hypervolumen) bei gleichem Radius geordnet werden. Jedes größere Polytop in der Sequenz ist runder als sein Vorgänger, mehr Inhalt innerhalb des gleichen Radius einschließen. Der 4-Simplex (5-Zellen) ist der kleinste Grenzfall und der 120-Zellen-Fall der größte. Die Komplexität (gemessen durch Vergleichen der Konfigurationsmatrizen oder einfach der Anzahl der Eckpunkte) folgt der gleichen Reihenfolge. Dies bietet ein alternatives numerisches Benennungsschema für reguläre Polytope, bei denen die 24-Zelle das 24-Punkt-4-Polytop ist: das vierte in der aufsteigenden Sequenz, die vom 5-Punkt-4-Polytop zum 600-Punkt-4-Polytop verläuft.
- ^ Die Kantenlänge ist immer unterschiedlich, es sei denn, Vorgänger und Nachfolger sind es beide radial gleichseitig, dh ihre Kantenlänge ist die gleich als ihr Radius (so bleiben beide erhalten). Da radial gleichseitige Polytope[b] sind selten, es scheint, dass die einzige solche Konstruktion (in jeder Dimension) von 8-Zellen bis 24-Zellen besteht, was die 24-Zellen zum einzigartigen regulären Polytop (in jeder Dimension) macht, das die gleiche Kantenlänge wie sein Vorgänger hat mit dem gleichen Radius.
- ^ ein b Bis zu 6 Ebenen können in 4 Dimensionen zueinander orthogonal sein. Der dreidimensionale Raum nimmt nur 3 senkrechte Achsen und 3 senkrechte Ebenen durch einen einzelnen Punkt auf. Im 4-dimensionalen Raum können wir 4 senkrechte Achsen und 6 senkrechte Ebenen durch einen Punkt haben (aus dem gleichen Grund, aus dem der Tetraeder 6 Kanten hat, nicht 4): Es gibt 6 Möglichkeiten, 4 Dimensionen 2 gleichzeitig zu nehmen. Drei solcher Paare (senkrechte Ebenen) treffen sich an jedem Scheitelpunkt (aus demselben Grund, aus dem sich drei Kanten des Tetraeders an jedem Scheitelpunkt treffen).
- ^ Die Kanten der Quadrate sind an den Gitterlinien dieses Koordinatensystems ausgerichtet. Zum Beispiel:
( 0, –1, 1, 0) ( 0, 1, 1, 0)
( 0, –1, –1, 0) ( 0, 1, –1, 0)
ist das Quadrat in der xy Flugzeug. Die Kanten der Quadrate sind keine Kanten mit 24 Zellen, sondern innere Akkorde, die zwei Eckpunkte 90 verbindenÖ voneinander entfernt; Die Quadrate sind also lediglich unsichtbare Konfigurationen von vier Eckpunkten der 24-Zellen, keine sichtbaren 24-Zellen-Merkmale. - ^ ein b c d Zwei Ebenen im 4-dimensionalen Raum können vier mögliche wechselseitige Positionen haben: (1) sie können zusammenfallen (genau dieselbe Ebene sein); (2) sie können parallel sein (der einzige Weg, auf dem sie sich überhaupt nicht schneiden können); (3) sie können sich in einer einzigen Linie schneiden, wie es zwei nicht parallele Ebenen im dreidimensionalen Raum tun; oder (4) Sie können sich in einem einzigen Punkt schneiden: und sie Muss, wenn und nur wenn sie vollständig sind[z] aufrecht;; Dies ist die überraschende, nicht intuitive Sache darüber, wie sich Ebenen im 4-Raum schneiden.
- ^ Die Kanten der orthogonalen äquatorialen Quadrate sind nicht ausgerichtet mit den Gitterlinien des Einheitsradius-Koordinatensystems. Die Quadrate liegen in den 6 orthogonalen Ebenen des Koordinatensystems, aber ihre Kanten sind die √2 Diagonalen von Einheitskantenlängenquadraten des Koordinatengitters. Zum Beispiel:
( 0, 0, 1, 0)
( 0, –1, 0, 0) ( 0, 1, 0, 0)
( 0, 0, –1, 0)
ist das Quadrat in der xy Flugzeug. Beachten Sie, dass die 8 ganze Zahl Koordinaten umfassen die Eckpunkte der 6 orthogonalen Quadrate. - ^ ein b c Die senkrechten Sechsecke sind in Bezug auf die orthogonalen Ebenen des Einheitsradius-Koordinatensystems geneigt (geneigt). Jedes Sechseck besteht aus 3 Paaren gegenüberliegender Eckpunkte (drei 24-Zellen-Durchmesser): einem gegenüberliegenden Paar von ganze Zahl Koordinatenscheitelpunkte (eine der vier Koordinatenachsen) und zwei gegenüberliegende Paare von halbe ganze Zahl Koordinatenscheitelpunkte (keine Koordinatenachsen). Zum Beispiel:
( 0, 0, 1, 0)
( 1/.2, –1/.2, 1/.2, –1/.2) ( 1/.2, 1/.2, 1/.2, 1/.2)
(-1/.2, –1/.2, –1/.2, –1/.2) (-1/.2, 1/.2, –1/.2, 1/.2)
( 0, 0, –1, 0)
ist ein Sechseck auf der y Achse. im Gegensatz zu den √2 Quadrate, die Sechsecke bestehen tatsächlich aus 24-Zellen-Kanten, so dass sie sichtbare Merkmale der 24-Zellen sind. - ^ ein b Es ist natürlich schwierig, vier hexagonale Ebenen zu visualisieren, die alle senkrecht zueinander stehen. Man kann sie im Kuboktaeder sehen (eine Projektion der 24-Zellen in 3-Dimensionen), wo sie in einem Winkel von 60 Grad zueinander zu stehen scheinen. In der dreidimensionalen Projektion scheinen sich zwei von vier nicht orthogonalen Sechsecken an jedem der 12 Eckpunkte zu schneiden, aber dies sind tatsächlich 16 Sechsecke und 24 Eckpunkte. In 4 Dimensionen schneiden sich 4 nicht orthogonale Sechsecke an jedem Scheitelpunkt, aber auch vier orthogonale Sechsecke schneiden sich nur in ihrem gemeinsamen Zentrum, so dass jedes von ihnen einen disjunkten Satz von 6 der 24 Scheitelpunkte durchläuft.
- ^ ein b Diese Dreiecke liegen in denselben orthogonalen Ebenen, die die Sechsecke enthalten.[j] zwei Dreiecke mit Kantenlänge √3 sind in jedes Sechseck eingeschrieben. Zum Beispiel in Einheitsradiuskoordinaten:
( 0, 0, 1, 0)
( 1/.2, –1/.2, 1/.2, –1/.2) ( 1/.2, 1/.2, 1/.2, 1/.2)
(-1/.2, –1/.2, –1/.2, –1/.2) (-1/.2, 1/.2, –1/.2, 1/.2)
( 0, 0, –1, 0)
sind zwei gegenüberliegende zentrale Dreiecke auf der y Achse, wobei jedes Dreieck durch die Eckpunkte in abwechselnden Reihen gebildet wird. Im Gegensatz zu den Sechsecken ist die √3 Dreiecke bestehen nicht aus tatsächlichen 24-Zellen-Kanten, daher sind sie unsichtbare Merkmale der 24-Zellen-Kanten wie die √2 Quadrate. - ^ Dies sind nicht die orthogonalen Ebenen des Koordinatensystems; Die Kanten dieser Dreiecke sind die Diagonalen der kubischen Zellen des Koordinatengitters des Einheitsradius der Länge √3.
- ^ Sie umgeben den Scheitelpunkt (im dreidimensionalen Raum der Grenzfläche der 24 Zellen) so, wie die 8 Ecken eines Würfels seine Mitte umgeben. (Die Scheitelpunktzahl der 24-Zellen ist ein Würfel.)
- ^ Sie umgeben den Scheitelpunkt im dreidimensionalen Raum so, wie die 6 Ecken eines Oktaeders seine Mitte umgeben.
- ^ ein b Innenmerkmale werden nicht als Elemente des Polytops betrachtet. Zum Beispiel ist das Zentrum einer 24-Zellen-Zelle ein bemerkenswertes Merkmal (ebenso wie ihre langen Radien), aber diese inneren Merkmale zählen nicht als Elemente in ihrer Konfigurationsmatrix, die nur elementare Merkmale zählt (diejenigen, die sich nicht in einem anderen befinden) Merkmal einschließlich des Polytops selbst). Innenausstattung wird in den meisten Diagrammen und Abbildungen in diesem Artikel nicht gerendert (sie sind normalerweise unsichtbar). In Abbildungen, die Innenmerkmale zeigen, zeichnen wir Innenkanten immer als gestrichelte Linien, um sie von Elementarkanten zu unterscheiden.
- ^ ein b Der zentrale Scheitelpunkt ist a kanonische Spitze weil es eine Kantenlänge ist, die äquidistant von den gewöhnlichen Eckpunkten in der 4. Dimension ist, da die Spitze einer kanonischen Pyramide eine Kantenlänge äquidistant von ihren anderen Eckpunkten ist.
- ^ Also (√1, √2, √3, √4) sind die Vertex-Akkordlängen des Tesseracts sowie der 24-Zellen. Sie sind auch die Durchmesser des Tesserakts (von kurz bis lang), jedoch nicht der 24-Zellen.
- ^ Wenn der pythagoreische Abstand zwischen zwei beliebigen Eckpunkten ist √1beträgt ihre geodätische Entfernung 1; Sie können zwei benachbarte Scheitelpunkte (im gekrümmten 3-Raum der Oberfläche) oder ein Scheitelpunkt und das Zentrum (im 4-Raum) sein. Wenn ihre pythagoreische Entfernung ist √2beträgt ihre geodätische Entfernung 2 (ob über 3-Raum oder 4-Raum, da der Pfad entlang der Kanten dieselbe gerade Linie mit einer 90 istÖ biegen Sie es als den Weg durch die Mitte). Wenn ihre pythagoreische Entfernung ist √3beträgt ihre geodätische Entfernung immer noch 2 (ob auf einem sechseckigen Großkreis nach einer 60)Ö Biegung oder als gerade Linie mit einer 60Ö biegen Sie es durch die Mitte). Schließlich, wenn ihre pythagoreische Entfernung ist √4Ihre geodätische Entfernung beträgt immer noch 2 im 4-Raum (direkt durch die Mitte), aber sie erreicht 3 im 3-Raum (indem sie sich auf halber Strecke um einen sechseckigen Großkreis bewegt).
- ^ ein b c d e Die Scheitelpunktfigur ist die Facette, die durch Abschneiden eines Scheitelpunkts erstellt wird. kanonisch an den auf den Scheitelpunkt einfallenden Mittelkanten. Man kann jedoch ähnliche Scheitelpunktfiguren mit unterschiedlichen Radien erstellen, indem man an einem beliebigen Punkt entlang dieser Kanten abschneidet, bis einschließlich an den benachbarten Scheitelpunkten, um a zu schneiden volle Größe Scheitelpunktfigur. Das dient hier dem veranschaulichenden Zweck.
- ^ Acht √1 Kanten konvergieren im dreidimensionalen Raum von den Ecken der kubischen Scheitelpunktfigur der 24 Zellen[t] und treffen sich in seiner Mitte (dem Scheitelpunkt), wo sie 4 gerade Linien bilden, die sich dort kreuzen. Die 8 Eckpunkte des Würfels sind die acht nächstgelegenen anderen Eckpunkte der 24-Zellen. Die geraden Linien sind Geodäten: zwei √1-Längensegmente einer scheinbar geraden Linie (im 3-Raum der gekrümmten Oberfläche der 24-Zelle), die in der 4. Dimension zu einem Großkreis-Sechseck (im 4-Raum) gebogen ist. Aus diesem gekrümmten 3-Raum heraus sind die Biegungen in den Sechsecken unsichtbar. Von außen (wenn wir die 24-Zellen im 4-Raum betrachten könnten) würden sich die geraden Linien in der 4. Dimension an den Würfelzentren verbiegen, da das Zentrum in der 4. Dimension außerhalb der definierten Hyperebene nach außen verschoben ist durch die Eckpunkte des Würfels. Somit ist der Scheitelpunktwürfel tatsächlich eine kubische Pyramide.
- ^ Sechs √2 Akkorde konvergieren im 3-Raum von den Gesichtsmitten der kubischen Scheitelpunktfigur der 24 Zellen[t] und treffen sich in seiner Mitte (dem Scheitelpunkt), wo sie 3 gerade Linien bilden, die sich dort senkrecht kreuzen. Die 8 Eckpunkte des Würfels sind die acht nächstgelegenen anderen Eckpunkte der 24-Zellen und acht √1 Kanten konvergieren von dort, aber lassen Sie uns sie jetzt ignorieren, da 7 gerade Linien, die sich in der Mitte kreuzen, verwirrend sind, um alle auf einmal zu visualisieren. Jeder der sechs √2 Akkorde verlaufen von der Mitte dieses Würfels (dem Scheitelpunkt) durch eine Gesichtsmitte zur Mitte eines benachbarten (flächengebundenen) Würfels, der ein weiterer Scheitelpunkt der 24-Zellen ist: kein nächster Scheitelpunkt (an den Würfelecken), sondern einer befindet sich 90 ° entfernt in einer zweiten konzentrischen Schale von sechs √2-entfernte Eckpunkte, die die erste Schale von acht umgeben √1-entfernte Eckpunkte. Das Gesichtszentrum, durch das die √2 Akkordpässe sind der Mittelpunkt des √2 Akkord, so liegt es in der 24-Zellen.
- ^ Man kann die 24-Zellen durch 6 Eckpunkte (in jeder hexagonalen Großkreisebene) oder durch 4 Eckpunkte (in jeder quadratischen Großkreisebene) in zwei gleiche Teile schneiden. Man kann dies im Kuboktaeder (der zentralen Hyperebene der 24-Zellen) sehen, wo es vier sechseckige Großkreise (entlang der Kanten) und sechs quadratische Großkreise (diagonal über die quadratischen Flächen) gibt.
- ^ Acht √3 Akkorde laufen aus den Ecken der kubischen Scheitelpunktfigur der 24 Zellen zusammen[t] und treffen sich in seiner Mitte (dem Scheitelpunkt), wo sie 4 gerade Linien bilden, die sich dort kreuzen. Jeder der acht √3 Die Akkorde verlaufen von der Mitte dieses Würfels zur Mitte eines diagonal benachbarten (vertexgebundenen) Würfels, der ein weiterer Scheitelpunkt der 24-Zellen ist: einer befindet sich 120 ° entfernt in einer dritten konzentrischen Achtschale √3-entfernte Eckpunkte, die die zweite Sechserschale umgeben √2-entfernte Eckpunkte, die die erste Schale von acht umgeben √1-entfernte Eckpunkte.
- ^ Jedes Paar parallel √1 Kanten verbinden ein Paar von parallelen √3 Akkorde bilden eines von 48 Rechtecken und jedes Paar parallel √2 Akkorde verbinden ein weiteres Paar von Parallelen √2 Akkorde bilden eines von 18 Quadraten.
- ^ ein b Man nennt zwei flache Ebenen A und B eines euklidischen Raumes von vier Dimensionen vollständig orthogonal genau dann, wenn jede Linie in A orthogonal zu jeder Linie in B ist. In diesem Fall schneiden sich die Ebenen A und B an einem einzelnen Punkt O, so dass sich eine Linie in A mit einer Linie in B schneidet, wenn sie sich bei O schneidet.
- ^ Jede Großkreisebene schneidet sich mit den anderen Großkreisebenen, zu denen sie nicht orthogonal ist √4 Durchmesser der 24-Zellen. Somit teilen sich zwei nicht orthogonale Quadrate oder Sechsecke zwei gegenüberliegende Eckpunkte, im Gegensatz zu zwei orthogonalen Großkreispolygonen, die außer ihrem gemeinsamen Zentrum keine Punkte gemeinsam haben. Zwei nicht orthogonale Großkreisdreiecke teilen sich nur einen Scheitelpunkt, da ihnen entgegengesetzte Scheitelpunkte fehlen.
- ^ Die 600-Zellen sind größer als die 24-Zellen und enthalten die 24-Zellen als Innenmerkmal. Die reguläre 5-Zelle findet im Inneren kein 4-Polytop außer der 120-Zelle, obwohl jedes 4-Polytop in unregelmäßige 5-Zellen zerlegt werden kann.
- ^ Wir können einen Scheitelpunkt mit einem 0-dimensionalen Schneidinstrument (wie der Spitze eines Messers oder dem Kopf eines Reißverschlusses) von einem Polygon abschneiden, indem wir ihn entlang einer eindimensionalen Linie streichen und eine neue Kante freigeben. Wir können einen Scheitelpunkt eines Polyeders mit einer eindimensionalen Schneide (wie ein Messer) abschneiden, indem wir ihn durch eine zweidimensionale Gesichtsebene streichen und ein neues Gesicht freigeben. Wir können einen Scheitelpunkt von einem Polychoron (einem 4-Polytop) mit einer zweidimensionalen Schnittebene (wie einem Schneepflug) abschneiden, indem wir ihn durch ein dreidimensionales Zellvolumen streichen und eine neue Zelle freilegen. Beachten Sie, dass wie innerhalb der neuen Kantenlänge des Polygons oder des neuen Flächenbereichs des Polyeders jeder Punkt innerhalb des neuen Zellvolumens jetzt auf der Oberfläche des Polychors freigelegt ist.
- ^ Jede Zellflächenebene schneidet sich mit den anderen Gesichtsebenen ihrer Art, zu denen sie an ihrer charakteristischen Scheitelpunktsehnenkante nicht vollständig orthogonal oder parallel ist. Es mag paradox erscheinen, dass sich benachbarte Flächenebenen von orthogonal gerichteten Zellen (wie Würfel) an einer Kante schneiden (wie dies offensichtlich der Fall ist), da Ebenen sich nicht im 4-Raum schneiden dürfen (außer an einem einzelnen Punkt). wenn sie vollständig orthogonal sind.[h] Die Auflösung dieses offensichtlichen Paradoxons besteht darin, dass benachbarte Flächenebenen solcher 4-Polytopzellen dies nicht sind vollständig[z] orthogonal im 4-Raum. Obwohl ihr Diederwinkel im Grenzraum 3 90 Grad beträgt, liegen sie in derselben Hyperebene (sie fallen in der vierten Dimension eher zusammen als senkrecht); Somit schneiden sie sich in einer Linie, wie es nicht parallele Ebenen in jedem 3-Raum tun.
- ^ Die einzigen Ebenen durch genau 6 Eckpunkte der 24-Zellen (ohne den zentralen Eckpunkt) sind die 16 hexagonalen Großkreise. Es gibt keine Ebenen durch genau 5 Eckpunkte. Es gibt verschiedene Arten von Ebenen durch genau 4 Eckpunkte: die 18 √2 quadratische große Kreise, die 72 √1 quadratische (tesseract) Gesichter und 144 √1 durch √2 Rechtecke. Die Ebenen durch genau 3 Eckpunkte sind die 96 √2 gleichseitige Dreiecksflächen (16 Zellen) und die 96 √1 gleichseitige Dreiecksflächen (24 Zellen).
- ^ Die kubische Scheitelpunktzahl der 24 Zellen[t] wurde auf eine tetraedrische Scheitelpunktfigur abgeschnitten (siehe Keplers Zeichnung). Der Scheitelpunktwürfel ist verschwunden, und jetzt gibt es nur noch 4 Ecken der Scheitelpunktfigur, wo es zuvor 8 gab. Vier Tesseraktkanten laufen von den Tetraederscheitelpunkten zusammen und treffen sich in ihrer Mitte, wo sie sich nicht kreuzen (da der Tetraeder keine Gegensätze hat) Eckpunkte).
- ^ ein b c Der gemeinsame Kern ist die 24-Zellen-Doppel-24-Zelle mit Kantenlänge und Radius 1/2. Das Korrigieren einer der drei 16-Zellen zeigt diese kleinere 24-Zelle, die einen 4-Gehalt von nur 1/8 (1/16 des 24-Zellen) aufweist. Seine Eckpunkte liegen in den Zentren der oktaedrischen Zellen der 24 Zellen, die auch die Zentren der quadratischen Flächen der Tesserakte sind, und sind auch die Zentren der Kanten der 16 Zellen.
- ^ Die kubische Scheitelpunktzahl der 24 Zellen[t] wurde auf eine oktaedrische Scheitelpunktfigur abgeschnitten. Der Scheitelpunktwürfel ist verschwunden, und jetzt gibt es nur noch 6 Ecken der Scheitelpunktfigur, wo vorher 8 waren. Die 6 √2 Akkorde, die früher von Würfelflächenzentren konvergierten, konvergieren jetzt von Oktaederscheitelpunkten; aber nach wie vor treffen sie sich in der Mitte, wo sich 3 gerade Linien senkrecht kreuzen. Die Oktaederscheitelpunkte befinden sich 90 ° außerhalb des verschwundenen Würfels an den neuen nächstgelegenen Scheitelpunkten. Vor dem Abschneiden waren dies Scheitelpunkte mit 24 Zellen in der zweiten Schale der umgebenden Scheitelpunkte.
- ^ Die 24 Eckpunkte der 24-Zellen, die jeweils zweimal verwendet werden, sind die Eckpunkte von drei 16-Eckpunkt-Tesserakten.
- ^ Die 24 Eckpunkte der 24-Zellen, die jeweils einmal verwendet werden, sind die Eckpunkte von drei 16-Zellen mit 8 Eckpunkten.
- ^ Die Kanten der 16 Zellen werden in keinem der Renderings in diesem Artikel angezeigt. Wenn wir Innenkanten zeigen wollten, konnten sie als gestrichelte Linien gezeichnet werden. Die Kanten der eingeschriebenen Tesserakte sind immer sichtbar, da sie auch Kanten der 24-Zellen sind.
- ^ Der 4-dimensionale Inhalt des Einheits-Kantenlängen-Tesserakts ist 1 (per Definition). Der Inhalt der 24-Zellen-Einheitskantenlänge beträgt 2, sodass sich die Hälfte ihres Inhalts in jedem Tesseract und die Hälfte zwischen ihren Umschlägen befindet. Jeweils 16 Zellen (Kantenlänge √2) schließt einen Inhalt von 2/3 ein, wobei 1/3 eines einschließenden Tesserakts zwischen ihren Umschlägen verbleibt.
- ^ Zwischen der 24-Zellen-Hülle und der 8-Zellen-Hülle befinden sich die 8 kubischen Pyramiden von Gossets Konstruktion. Zwischen der 8-Zellen-Hülle und der 16-Zellen-Hülle befinden sich 16 rechte tetraedrische Pyramiden, deren Spitzen die Ecken des Tesserakts ausfüllen.
- ^ ein b Dreidimensionale Rotationen treten um eine Achsenlinie auf. Vierdimensionale Rotationen können um eine Ebene herum auftreten. In drei Dimensionen können wir also Ebenen um eine gemeinsame Linie falten (wie beim Falten eines flachen Netzes von 6 Quadraten zu einem Würfel), und in vier Dimensionen können wir Zellen um eine gemeinsame Ebene falten (wie beim Falten eines flachen Netzes von 8 Würfeln) bis in einen Tesserakt). Das Falten um ein quadratisches Gesicht ist nur das Falten zwei seiner orthogonalen Kanten gleichzeitig;; Es gibt nicht genug Platz in drei Dimensionen, um dies zu tun, genauso wie es nicht genug Platz in zwei Dimensionen gibt, um um eine Linie zu falten (nur genug, um um einen Punkt zu falten).
- ^ Dies scheint zunächst winkellos unmöglich zu sein, und tatsächlich wäre es in einem flachen Raum von nur drei Dimensionen. Wenn zwei Würfel in einem gewöhnlichen dreidimensionalen Raum (z. B. auf der Oberfläche eines Tisches in einem gewöhnlichen dreidimensionalen Raum) von Angesicht zu Angesicht ruhen, passt ein Oktaeder so in sie hinein, dass vier seiner sechs Eckpunkte an den vier liegen Ecken der quadratischen Fläche zwischen den beiden Würfeln; Aber dann liegen die anderen beiden oktaedrischen Eckpunkte nicht an einer Würfelecke (sie fallen in das Volumen der beiden Würfel, aber nicht an einen Würfelscheitelpunkt). In vier Dimensionen sind jedoch die Grenz-3-Räume von 4-Polytopen gebogen. Die 3-Mannigfaltigkeit der Grenze des Tesserakts (eine Tessellation der 3-Kugel durch 8 Würfel) ist um seine quadratischen Flächenebenen gefaltet.[an] so dass die benachbarten flächengebundenen Würfel relativ zueinander ausgerichtet sind, so dass alle 6 Eckpunkte des Oktaeders am Scheitelpunkt eines Würfels liegen.
- ^ Betrachten Sie die drei senkrecht √2 lange Durchmesser der oktaedrischen Zelle. Zwei davon sind die Gesichtsdiagonalen der quadratischen Fläche zwischen zwei Würfeln; jeder ist ein √2
Akkord, der zwei Eckpunkte dieser 8-Zellen-Würfel über eine quadratische Fläche verbindet, zwei Eckpunkte von zwei 16-Zellen-Tetraedern (in die Würfel eingeschrieben) und zwei gegenüberliegende Eckpunkte eines 24-Zellen-Oktaeders (diagonal über zwei der drei) verbindet orthogonale quadratische Mittelabschnitte). Der dritte senkrechte lange Durchmesser des Oktaeders macht genau das Gleiche (durch Symmetrie); So verbindet es auch zwei Eckpunkte eines Würfelpaares über ihre gemeinsame quadratische Fläche (aber ein anderes Würfelpaar als eines der anderen Tesserakte in der 24-Zellen-Zelle).
- ^ Eine Möglichkeit, das zu visualisieren n-dimensionale Hyperebenen ist wie die n-spaces, die definiert werden können durch n + 1 Punkte. Ein Punkt ist der 0-Raum, der durch 1 Punkt definiert ist. Eine Linie ist der 1-Raum, der durch 2 Punkte definiert ist, die nicht zusammenfallen. Eine Ebene ist der 2-Raum, der durch 3 Punkte definiert ist, die nicht kolinear sind (ein beliebiges Dreieck). Im 4-Raum ist eine 3-dimensionale Hyperebene der 3-Raum, der durch 4 Punkte definiert ist, die nicht koplanar sind (irgendein Tetraeder). Im 5-Raum ist eine 4-dimensionale Hyperebene der 4-Raum, der durch 5 Punkte definiert ist, die nicht cocellular sind (jede 5-Zellen). Diese Simplex-Figuren teilen die Hyperebene in zwei Teile (innerhalb und außerhalb der Figur), aber zusätzlich teilen sie das Universum (den umschließenden Raum) in zwei Teile (über und unter der Hyperebene). Das n Punkte gebunden eine endliche Simplexfigur (von außen), und sie definieren eine unendliche Hyperebene (von innen). Diese beiden Unterteilungen sind orthogonal, so dass der definierende Simplex den Raum in sechs Bereiche unterteilt: innerhalb des Simplex und in der Hyperebene, innerhalb des Simplex, aber über oder unter der Hyperebene, außerhalb des Simplex, aber in der Hyperebene und außerhalb des Simplex über oder unter dem Hyperebene.
- ^ Es ist wichtig, die Radien nur als unsichtbare innere Merkmale der 24-Zellen (gestrichelte Linien) zu visualisieren, da sie keine Kanten der Wabe sind. Ebenso ist das Zentrum der 24-Zellen leer (kein Scheitelpunkt der Wabe).
- ^ Es gibt (mindestens) zwei Arten korrekter Dimensionsanalogien: die übliche Art zwischen Dimensionen n und Dimension n + 1 und die viel seltenere und weniger offensichtliche Art zwischen den Dimensionen n und Dimension n + 2. Ein Beispiel für Letzteres ist, dass Rotationen im 4-Raum um einen einzelnen Punkt stattfinden können, ebenso wie Rotationen im 2-Raum. Ein anderer ist der n-Sphärenregel, dass die Oberfläche der Kugel eingebettet in n+2 Dimensionen sind genau 2π r mal die Volumen eingeschlossen von der Kugel eingebettet in n Dimensionen, die bekanntesten Beispiele sind, dass der Umfang eines Kreises 2 istπ r mal 1, und die Oberfläche der gewöhnlichen Kugel ist 2π r mal 2r. Coxeter führt dies als einen Fall an, in dem uns die dimensionale Analogie als Methode scheitern kann, aber es ist wirklich unser Versagen, zu erkennen, ob eine ein- oder zweidimensionale Analogie die geeignete Methode ist.
- ^ Rotationen in vier Dimensionen können um eine Ebene herum auftreten, beispielsweise wenn benachbarte Zellen um ihre Schnittebene gefaltet werden (analog zu der Art und Weise, wie benachbarte Flächen um ihre Schnittlinie gefaltet werden).[an] In vier Dimensionen gibt es jedoch noch eine andere Möglichkeit, wie Rotationen auftreten können, die als Doppelrotation bezeichnet wird. Doppelrotationen sind ein emergentes Phänomen in der vierten Dimension und haben in drei Dimensionen keine Analogie: Das Aufklappen quadratischer Flächen und das Aufklappen kubischer Zellen sind Beispiele für einfache Rotationen, die einzige Art, die in weniger als vier Dimensionen auftritt. Bei dreidimensionalen Rotationen bleiben die Punkte in einer Linie während der Rotation fest, während sich jeder andere Punkt bewegt. Bei vierdimensionalen einfachen Rotationen bleiben die Punkte in einer Ebene während der Rotation fixiert, während sich jeder zweite Punkt bewegt. Bei 4-dimensionalen Doppelrotationen bleibt ein Punkt während der Rotation fest und jeder zweite Punkt bewegt sich (wie bei einer zweidimensionalen Rotation!). Dies ist eines von mehreren überraschenden, kontraintuitiven Dingen über Rotationen im 4-Raum.[as]
Zitate[edit]
- ^ Coxeter 1973, p. 298, Tabelle V: Die Verteilung der Eckpunkte vierdimensionaler Polytope in parallelen festen Abschnitten (§13.1); (i) Abschnitte von {3,4,3} (Kante 2), die mit einem Scheitelpunkt beginnen; siehe Spalte ein.
- ^ Coxeter 1973, p. 302, Tabelle VI (ii) II = {3,4,3}, Ergebnisspalte.
- EIN_und_Abb_8.2B._42-0 “> ^ Coxeter 1973, S. 149-150, §8.22. siehe Abbildungen Abb. 8.2EIN und Abb. 8.2B.
Verweise[edit]
- Kepler, Johannes (1619). Harmonices Mundi (Die Harmonie der Welt). Johann Planck.
- Banchoff, Thomas F. (2013). “Torus-Zersetzung regulärer Polytope im 4-Raum”. In Senechal, Marjorie (Hrsg.). Raum gestalten. Springer New York. pp. 257–266. doi:10.1007 / 978-0-387-92714-5_20. ISBN 978-0-387-92713-8.
- Coxeter, HSM (1973) [1948]. Regelmäßige Polytope (3. Aufl.). New York: Dover.
- Coxeter, HSM (1991), Regelmäßige komplexe Polytope (2. Aufl.), Cambridge: Cambridge University Press
- Coxeter, HSM (1995), Sherk, F. Arthur; McMullen, Peter; Thompson, Anthony C.; Weiss, Asia Ivic (Hrsg.), Kaleidoskope: Ausgewählte Schriften von HSM Coxeter (2. Aufl.), Wiley-Interscience Publication, ISBN 978-0-471-01003-6
- (Papier 22) HSM Coxeter, Regelmäßige und halbregelmäßige Polytope I., [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Papier 23) HSM Coxeter, Regelmäßige und halbregelmäßige Polytope II, [Math. Zeit. 188 (1985) 559-591]
- (Papier 24) HSM Coxeter, Regelmäßige und halbregelmäßige Polytope III, [Math. Zeit. 200 (1988) 3-45]
- Ghyka, Matila (1977). Die Geometrie von Kunst und Leben. New York: Dover-Veröffentlichungen. ISBN 978-0-486-23542-4.
- Johnson, Norman (2018), Geometrien und Transformationen, Cambridge: Cambridge University Press, ISBN 978-1-107-10340-5
- Johnson, Norman (1991), Einheitliche Polytope (Manuskript ed.)
- Johnson, Norman (1966), Die Theorie der einheitlichen Polytope und Waben (Ph.D. ed.)
- Weisstein, Eric W. “24-Zellen”. MathWorld. (auch unter Icositetrachoron)
- Klitzing, Richard. 4D-Uniformpolytope (Polychora) x3o4o3o – ico.
- Olshevsky, George. “Icositetrachoron”. Glossar für den Hyperraum. Archiviert von das Original am 4. Februar 2007.
- Der 24-Zeller (24-Zellen) Marco Möllers regelmäßige Polytope in R.4 (Deutsche)




 hat eine reale Darstellung als 24-Zellen im 4-dimensionalen Raum. 3{4}3 hat 24 Eckpunkte und 24 3-Kanten. Seine Symmetrie ist 3[4]3, Bestellung 72.
hat eine reale Darstellung als 24-Zellen im 4-dimensionalen Raum. 3{4}3 hat 24 Eckpunkte und 24 3-Kanten. Seine Symmetrie ist 3[4]3, Bestellung 72.
Recent Comments