Jaccard-Index – Wikipedia
Maß für Ähnlichkeit und Vielfalt zwischen Sets
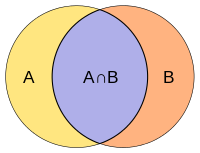

Schnitt und Vereinigung zweier Mengen A und B
Die Jaccard-Index, auch bekannt als die Jaccard-Ähnlichkeitskoeffizient, ist eine Statistik, die zum Messen der Ähnlichkeit und Vielfalt von Stichprobensätzen verwendet wird. Es wurde von Paul Jaccard entwickelt und gab ursprünglich den französischen Namen Koeffizient de communauté,[1] und unabhängig wieder von T. Tanimoto formuliert.[2] Und so kam es dass der Tanimoto-Index oder Tanimoto-Koeffizient werden auch in einigen Bereichen verwendet. Sie sind jedoch identisch, indem sie im Allgemeinen das Verhältnis von Kreuzung über Union. Der Jaccard-Koeffizient misst die Ähnlichkeit zwischen endlichen Stichprobensätzen und ist definiert als die Größe des Schnittpunkts geteilt durch die Größe der Vereinigung der Stichprobensätze:
Beachten Sie, dass konstruktionsbedingt
Wenn EIN und B sind beide leer, definieren J(EIN,B) = 1. Der Jaccard-Koeffizient wird häufig in der Informatik, Ökologie, Genomik und anderen Wissenschaften verwendet, in denen binäre oder binarisierte Daten verwendet werden. Für die Hypothesenprüfung mit dem Jaccard-Koeffizienten stehen sowohl die exakte Lösungs- als auch die Näherungsmethode zur Verfügung.[3]
Jaccard-Ähnlichkeit gilt auch für Taschen, dh Multisets. Dies hat eine ähnliche Formel,[4] aber die Symbole bedeuten Sackschnitt und Sacksumme (nicht Vereinigung). Der Höchstwert ist 1/2.
Die Jackcard-Abstand, welche Maßnahmen disÄhnlichkeit zwischen Stichprobenmengen, ist komplementär zum Jaccard-Koeffizienten und wird durch Subtrahieren des Jaccard-Koeffizienten von 1 oder äquivalent durch Dividieren der Differenz der Größen der Vereinigung und der Schnittmenge zweier Mengen durch die Größe der Vereinigung erhalten:
Eine alternative Interpretation des Jaccard-Abstands ist das Verhältnis der Größe der symmetrischen Differenz
zur Gewerkschaft. Die Jaccard-Distanz wird häufig verwendet, um an . zu berechnen n × n Matrix zum Clustern und multidimensionalen Skalieren von n Mustersets.
Dieser Abstand ist eine Metrik für die Sammlung aller endlichen Mengen.[5][6][7]
Es gibt auch eine Version der Jaccard-Distanz für Maße, einschließlich Wahrscheinlichkeitsmaßen. Wenn
ist ein Maß auf einem messbaren Raum
, dann definieren wir den Jaccard-Koeffizienten durch
und die Jaccard-Distanz um
Vorsicht ist geboten, wenn
oder
, da diese Formeln in diesen Fällen nicht gut definiert sind.
Das min-weise unabhängige Permutationen-Hashing-Schema von MinHash kann verwendet werden, um effizient eine genaue Schätzung des Jaccard-Ähnlichkeitskoeffizienten von Paaren von Mengen zu berechnen, wobei jede Menge durch eine Signatur konstanter Größe repräsentiert wird, die aus den Minimalwerten einer Hash-Funktion abgeleitet wird .
Ähnlichkeit asymmetrischer binärer Attribute[edit]
Bei zwei Objekten, EIN und B, jeder mit n binären Attributen ist der Jaccard-Koeffizient ein nützliches Maß für die Überlappung, die EIN und B mit ihren Attributen teilen. Jedes Attribut von EIN und B kann entweder 0 oder 1 sein. Die Gesamtzahl jeder Kombination von Attributen für beide EIN und B sind wie folgt angegeben:
- stellt die Gesamtzahl der Attribute dar, bei denen EIN und B beide haben einen Wert von 1.
- stellt die Gesamtzahl der Attribute dar, bei denen das Attribut von EIN ist 0 und das Attribut von B ist 1.
- stellt die Gesamtzahl der Attribute dar, bei denen das Attribut von EIN ist 1 und das Attribut von B ist 0.
- stellt die Gesamtzahl der Attribute dar, bei denen EIN und B beide haben den Wert 0.
|
EIN B |
0 | 1 |
|---|---|---|
| 0 | ||
| 1 |
Jedes Attribut muss in eine dieser vier Kategorien fallen, was bedeutet, dass
Der Jaccard-Ähnlichkeitskoeffizient, J, ist gegeben als
Die Jackcard-Distanz, DJ, ist gegeben als
Statistische Schlußfolgerungen können basierend auf den Jaccard-Ähnlichkeitskoeffizienten und folglich verwandten Metriken gemacht werden.[3] Gegeben zwei Beispielsätze EIN und B mit n Attribute kann ein statistischer Test durchgeführt werden, um festzustellen, ob eine Überlappung statistisch signifikant ist. Die genaue Lösung ist verfügbar, obwohl die Berechnung kostspielig sein kann, da n erhöht sich.[3] Schätzverfahren stehen entweder durch Approximation einer Multinomialverteilung oder durch Bootstrapping zur Verfügung.[3]
Differenz zum einfachen Matching-Koeffizienten (SMC)[edit]
Bei Verwendung für binäre Attribute ist der Jaccard-Index dem einfachen Matching-Koeffizienten sehr ähnlich. Der Hauptunterschied besteht darin, dass der SMC den Begriff
in Zähler und Nenner, während dies beim Jaccard-Index nicht der Fall ist. Somit zählt die SMC sowohl die gegenseitige Anwesenheit (wenn ein Attribut in beiden Sets vorhanden ist) als auch die gegenseitige Abwesenheit (wenn ein Attribut in beiden Sets fehlt) als Übereinstimmungen und vergleicht sie mit der Gesamtzahl der Attribute im Universum, während der Jaccard-Index zählt nur die gegenseitige Anwesenheit als Übereinstimmung und vergleicht sie mit der Anzahl der Attribute, die von mindestens einem der beiden Sets ausgewählt wurden.
Bei der Warenkorbanalyse beispielsweise enthält der Warenkorb von zwei Verbrauchern, die wir vergleichen möchten, möglicherweise nur einen kleinen Bruchteil aller verfügbaren Produkte im Geschäft, so dass der SMC in der Regel sehr hohe Ähnlichkeitswerte zurückgibt, selbst wenn die Warenkörbe sehr wenig Ähnlichkeit, was den Jaccard-Index in diesem Zusammenhang zu einem geeigneteren Maß für die Ähnlichkeit macht. Betrachten Sie zum Beispiel einen Supermarkt mit 1000 Produkten und zwei Kunden. Der Korb des ersten Kunden enthält Salz und Pfeffer und der Korb des zweiten enthält Salz und Zucker. In diesem Szenario würde die Ähnlichkeit zwischen den beiden Körben, gemessen durch den Jaccard-Index, 1/3 betragen, aber die Ähnlichkeit beträgt 0,998 unter Verwendung des SMC.
In anderen Kontexten, in denen 0 und 1 äquivalente Informationen (Symmetrie) tragen, ist der SMC ein besseres Ähnlichkeitsmaß. Beispielsweise würden Vektoren von demografischen Variablen, die in Dummy-Variablen wie Geschlecht gespeichert sind, besser mit dem SMC verglichen als mit dem Jaccard-Index, da der Einfluss des Geschlechts auf die Ähnlichkeit gleich sein sollte, unabhängig davon, ob männlich als 0 und weiblich definiert ist als 1 oder umgekehrt. Wenn wir jedoch symmetrische Dummy-Variablen haben, könnte man das Verhalten des SMC replizieren, indem man die Dummys in zwei binäre Attribute (in diesem Fall männlich und weiblich) aufteilt und sie so in asymmetrische Attribute umwandelt, was die Verwendung des Jaccard-Index ohne . ermöglicht jegliche Voreingenommenheit einführen. Der SMC bleibt jedoch im Fall von symmetrischen Dummy-Variablen recheneffizienter, da er keine zusätzlichen Dimensionen erfordert.
Gewichtete Jaccard-Ähnlichkeit und Entfernung[edit]
Wenn
und
sind zwei Vektoren mit allen reellen
, dann ist ihr Jaccard-Ähnlichkeitskoeffizient (damals auch als Ruzicka-Ähnlichkeit bekannt) definiert als
und Jaccard-Distanz (damals auch als Soergel-Distanz bekannt)
Noch allgemeiner gesagt, wenn
und
sind zwei nicht-negativ messbare Funktionen auf einem messbaren Raum
mit Maß
, dann können wir definieren
wo
und
sind punktweise Operatoren. Dann ist die Jackcard-Distanz
Dann zum Beispiel für zwei messbare Mengen
, wir haben
wo
und
sind die charakteristischen Funktionen der entsprechenden Menge.
Wahrscheinlichkeit Jaccard-Ähnlichkeit und Entfernung[edit]
Die oben beschriebene gewichtete Jaccard-Ähnlichkeit verallgemeinert den Jaccard-Index auf positive Vektoren, wobei eine Menge einem binären Vektor entspricht, der durch die Indikatorfunktion gegeben ist, dh
. Es verallgemeinert den Jaccard-Index jedoch nicht auf Wahrscheinlichkeitsverteilungen, bei denen eine Menge einer einheitlichen Wahrscheinlichkeitsverteilung entspricht, dh
Es ist immer weniger, wenn sich die Sets in der Größe unterscheiden. Wenn
dann
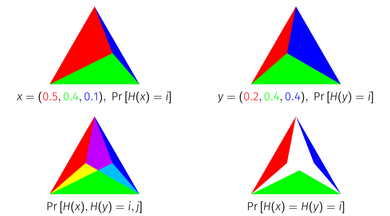
Stattdessen ist eine zwischen Wahrscheinlichkeitsverteilungen und ihren entsprechenden Unterstützungsmengen stetige Verallgemeinerung
die heißt die “Wahrscheinlichkeit” Jaccard.[8] Es hat die folgenden Grenzen gegenüber dem Weighted Jaccard auf Wahrscheinlichkeitsvektoren.
Hier ist die obere Schranke der (gewichtete) Sørensen-Dice-Koeffizient. Der entsprechende Abstand,
, ist eine Metrik über Wahrscheinlichkeitsverteilungen und eine Pseudometrik über nicht-negativen Vektoren.
Der Probability Jaccard Index hat eine geometrische Interpretation als die Fläche einer Schnittmenge von Simplizes. Jeder Punkt einer Einheit
-simplex entspricht einer Wahrscheinlichkeitsverteilung auf
Elemente, weil die Einheit
-simplex ist die Punktmenge in
Dimensionen, die sich zu 1 summieren. Um den Wahrscheinlichkeits-Jaccard-Index geometrisch abzuleiten, stellen Sie eine Wahrscheinlichkeitsverteilung als Einheitssimplex dar, unterteilt in Subsimplices entsprechend der Masse jedes Elements. Wenn Sie zwei so dargestellte Verteilungen übereinander legen und die zu jedem Element gehörenden Simplizes schneiden, entspricht die verbleibende Fläche dem Wahrscheinlichkeits-Jaccard-Index der Verteilungen.
Optimalität des Wahrscheinlichkeits-Jaccard-Index[edit]

Betrachten Sie das Problem, Zufallsvariablen so zu konstruieren, dass sie so weit wie möglich miteinander kollidieren. Das heißt, wenn
und
, wir möchten bauen
und
maximieren
. Wenn wir uns nur zwei Verteilungen ansehen
isoliert, das Höchste
wir erreichen können ist gegeben durch
wo
ist die Gesamtvariationsdistanz. Angenommen, es geht uns nicht nur um die Maximierung dieses bestimmten Paares, sondern wir möchten die Kollisionswahrscheinlichkeit eines beliebigen Paares maximieren. Man könnte unendlich viele Zufallsvariablen konstruieren, eine für jede Verteilung
, und versuchen zu maximieren
für alle Paare
. Der Probability Jaccard Index ist in einem ziemlich starken Sinne, der unten beschrieben wird, ein optimaler Weg, um diese Zufallsvariablen abzugleichen.
Für jede Probenahmemethode
und diskrete Verteilungen
, wenn
wo
![{displaystyle Pr[G(x)=G(z)]<J_{mathcal {P}}(x,z)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66ca35d4656cc676fc5ee3a8b24755c9da1d58ac)
![{displaystyle Pr[G(y)=G(z)]<J_{mathcal {P}}(y,z)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5863ec699546c3b1799683031e35c6a15017f0b)
Das heißt, keine Sampling-Methode kann mehr Kollisionen erreichen als
auf einem Paar, ohne weniger Kollisionen zu erzielen als
auf einem anderen Paar, bei dem das reduzierte Paar ähnlicher ist unter
als das erhöhte Paar. Dieser Satz gilt für den Jaccard-Index von Mengen (wenn er als Gleichverteilung interpretiert wird) und die Wahrscheinlichkeit Jaccard, aber nicht für den gewichteten Jaccard. (Der Satz verwendet das Wort “Probenahmeverfahren” eine gemeinsame Verteilung über alle Verteilungen auf einem Raum zu beschreiben, da sie sich aus der Verwendung von gewichteten Minhashing-Algorithmen ableitet, die dies als ihre Kollisionswahrscheinlichkeit erreichen.)
Dieser Satz hat einen visuellen Beweis für drei Elementverteilungen unter Verwendung der Simplex-Darstellung.
Tanimoto Ähnlichkeit und Entfernung[edit]
In der Literatur und im Internet kommen verschiedene Formen von Funktionen vor, die als Tanimoto-Ähnlichkeit und Tanimoto-Distanz beschrieben werden. Die meisten davon sind Synonyme für Jaccard-Ähnlichkeit und Jaccard-Distanz, aber einige sind mathematisch unterschiedlich. Viele Quellen[9] einen IBM Technical Report zitieren[2] als wegweisende Referenz. Der Bericht ist erhältlich bei mehrere Bibliotheken.
In “Ein Computerprogramm zur Klassifizierung von Pflanzen”, veröffentlicht im Oktober 1960,[10] ein Klassifikationsverfahren basierend auf einem Ähnlichkeitsverhältnis und einer abgeleiteten Distanzfunktion wird angegeben. Dies scheint die maßgeblichste Quelle für die Bedeutung der Begriffe zu sein “Tanimoto-Ähnlichkeit” und “Tanimoto-Distanz”. Das Ähnlichkeitsverhältnis entspricht der Jaccard-Ähnlichkeit, aber die Distanzfunktion ist nicht das gleiche wie die Jackcard-Distanz.
Tanimotos Definitionen von Ähnlichkeit und Distanz[edit]
In diesem Papier, a “Ähnlichkeitsverhältnis” wird über Bitmaps gegeben, wobei jedes Bit eines Arrays fester Größe das Vorhandensein oder Fehlen eines Merkmals in der modellierten Anlage darstellt. Die Definition des Verhältnisses ist die Anzahl der gemeinsamen Bits geteilt durch die Anzahl der gesetzten Bits (dh ungleich Null) in beiden Beispielen.
Mathematisch dargestellt, wenn Stichproben x und Ja sind Bitmaps,
ist der ichth bisschen x, und
sind bitweise und, oder Operatoren, dann ist das Ähnlichkeitsverhältnis
ist
Wenn jede Stichprobe stattdessen als ein Satz von Attributen modelliert wird, entspricht dieser Wert dem Jaccard-Koeffizienten der beiden Sätze. Jaccard wird in der Arbeit nicht zitiert, und es ist wahrscheinlich, dass die Autoren sich dessen nicht bewusst waren.
Tanimoto fährt fort, a . zu definieren “Distanzkoeffizient” basierend auf diesem Verhältnis, das für Bitmaps mit einer Ähnlichkeit ungleich null definiert ist:
Dieser Koeffizient ist bewusst kein Distanzmaß. Es wurde gewählt, um die Möglichkeit zu ermöglichen, dass zwei Exemplare, die sich stark voneinander unterscheiden, einem dritten ähneln. Es ist leicht, ein Beispiel zu konstruieren, das die Eigenschaft der Dreiecksungleichung widerlegt.
Andere Definitionen von Tanimoto-Distanz[edit]
Tanimoto-Distanz wird fälschlicherweise oft als Synonym für Jaccard-Distanz bezeichnet
. Diese Funktion ist eine geeignete Distanzmetrik. “Tanimoto-Distanz” wird oft als richtige Distanzmetrik angegeben, wahrscheinlich wegen der Verwechslung mit der Jaccard-Distanz.
Wenn Jaccard- oder Tanimoto-Ähnlichkeit über einen Bitvektor ausgedrückt wird, kann sie geschrieben werden als
wobei dieselbe Berechnung als Vektorskalarprodukt und Betrag ausgedrückt wird. Diese Darstellung beruht auf der Tatsache, dass für einen Bitvektor (bei dem der Wert jeder Dimension entweder 0 oder 1 ist) dann
und
Dies ist eine potenziell verwirrende Darstellung, da die über Vektoren ausgedrückte Funktion allgemeiner ist, es sei denn, ihr Bereich ist explizit eingeschränkt. Eigentum von
nicht unbedingt erweitern auf
. Insbesondere die Differenzfunktion
behält die Dreiecksungleichung nicht bei und ist daher keine richtige Distanzmetrik, wohingegen
ist.
Es besteht die reale Gefahr, dass die Kombination von “Tanimoto-Distanz” definiert mit dieser Formel zusammen mit der Anweisung “Die Tanimoto-Distanz ist eine richtige Distanzmetrik” führt zu dem falschen Schluss, dass die Funktion
ist in der Tat eine Distanzmetrik über Vektoren oder Mehrfachmengen im Allgemeinen, wohingegen ihre Verwendung in Ähnlichkeitssuch- oder Clusteralgorithmen möglicherweise keine korrekten Ergebnisse liefert.
Lipkus[6] verwendet eine Definition der Tanimoto-Ähnlichkeit, die äquivalent zu ist
, und bezieht sich auf die Tanimoto-Distanz als Funktion
. In der Arbeit wird jedoch klargestellt, dass der Kontext durch die Verwendung eines (positiven) Gewichtungsvektors eingeschränkt wird
so dass für jeden Vektor EIN in Betracht gezogen werden,
Unter diesen Umständen ist die Funktion eine geeignete Distanzmetrik, und so bildet ein Satz von Vektoren, der von einem solchen Gewichtungsvektor bestimmt wird, einen metrischen Raum unter dieser Funktion.
Jaccard-Index in Verwirrungsmatrizen für binäre Klassifikationen[edit]
In Konfusionsmatrizen, die für die binäre Klassifikation verwendet werden, kann der Jaccard-Index in die folgende Formel eingerahmt werden:
wobei TP die wahren Positiven sind, FP die falschen Positiven sind und FN die falschen Negativen sind und TN die wahren Negative sind.[11]
Siehe auch[edit]
Verweise[edit]
- ^ Jaccard, Paul (Februar 1912). “DIE VERTEILUNG DER FLORA IN DER ALPENZONE.1”. Neuer Phytologe. 11 (2): 37–50. mach:10.1111/j.1469-8137.1912.tb05611.x. ISSN 0028-646X.
- ^ ein B Tanimoto TT (17. November 1958). “Eine elementare mathematische Theorie der Klassifikation und Vorhersage”. Interner technischer IBM-Bericht. 1957 (8?).
- ^ ein B C D Chung NC, Miasojedow B, Startek M, Gambin A (Dezember 2019). “Jaccard/Tanimoto-Ähnlichkeitstest und Schätzmethoden für Daten zur biologischen Präsenz und Abwesenheit”. BMC Bioinformatik. 20 (Ergänzung 15): 644. doi:10.1186/s12859-019-3118-5. PMC 6929325. PMID 31874610.
- ^ Leskovec J, Rajaraman A, Ullman J (2020). Mining massiver Datensätze. Cambridge. ISBN 9781108476348. und P. 76-77 in einer früheren Version http://infolab.stanford.edu/~ullman/mmds/ch3.pdf
- ^ Kosub S (April 2019). “Eine Anmerkung zur Dreiecksungleichung für den Jaccard-Abstand”. Mustererkennungsbuchstaben. 120: 36–8. arXiv:1612.02696. mach:10.1016/j.patrec.2018.12.007.
- ^ ein B Lipkus AH (1999). “Ein Beweis der Dreiecksungleichung für den Tanimoto-Abstand”. Zeitschrift für Mathematische Chemie. 26 (1–3): 263–265. mach:10.1023/A:1019154432472.
- ^ Levandowsky M, Winter D (1971). “Abstand zwischen den Sätzen”. Natur. 234 (5): 34–35. mach:10.1038/234034a0.
- ^ ein B Moulton R, Jiang Y (2018). “Maximal konsistentes Sampling und der Jaccard-Index von Wahrscheinlichkeitsverteilungen”. Internationale Konferenz zum Thema Data Mining, Workshop zum hochdimensionalen Data Mining: 347–356. arXiv:1809.04052. mach:10.1109/ICDM.2018.00050. ISBN 978-1-5386-9159-5.
- ^ Zum Beispiel Huihuan Q, Xinyu W, Yangsheng X (2011). Intelligente Überwachungssysteme. Springer. P. 161. ISBN 978-94-007-1137-2.
- ^ Rogers DJ, Tanimoto TT (Oktober 1960). “Ein Computerprogramm zur Klassifizierung von Pflanzen”. Wissenschaft. 132 (3434): 1115–8. mach:10.1126/science.132.3434.1115. PMID 17790723.
- ^ Aziz Taha, Abdel (2015). “Metriken zur Bewertung der Segmentierung medizinischer 3D-Bilder: Analyse, Auswahl und Werkzeug”. BMC Medizinische Bildgebung. fünfzehn (29): 1–28. mach:10.1186/s12880-015-0068-x.
Weiterlesen[edit]
- Tan PN, Steinbach M, Kumar V (2005). Einführung in das Data Mining. ISBN 0-321-32136-7.
- Jaccard P (1901). “Étude Comparative de la Distribution florale dans une portion des Alpes et des Jura”. Bulletin de la Société vaudoise des sciences naturelles. 37: 547–579.
- Jaccard P (1912). “Die Verbreitung der Flora in der Alpenzone”. Neuer Phytologe. 11 (2): 37–50. mach:10.1111/j.1469-8137.1912.tb05611.x.

 Wenn EIN und B sind beide leer, definieren J(EIN,B) = 1. Der Jaccard-Koeffizient wird häufig in der Informatik, Ökologie, Genomik und anderen Wissenschaften verwendet, in denen binäre oder binarisierte Daten verwendet werden. Für die Hypothesenprüfung mit dem Jaccard-Koeffizienten stehen sowohl die exakte Lösungs- als auch die Näherungsmethode zur Verfügung.[3]
Wenn EIN und B sind beide leer, definieren J(EIN,B) = 1. Der Jaccard-Koeffizient wird häufig in der Informatik, Ökologie, Genomik und anderen Wissenschaften verwendet, in denen binäre oder binarisierte Daten verwendet werden. Für die Hypothesenprüfung mit dem Jaccard-Koeffizienten stehen sowohl die exakte Lösungs- als auch die Näherungsmethode zur Verfügung.[3]

 zur Gewerkschaft. Die Jaccard-Distanz wird häufig verwendet, um an . zu berechnen n × n Matrix zum Clustern und multidimensionalen Skalieren von n Mustersets.
zur Gewerkschaft. Die Jaccard-Distanz wird häufig verwendet, um an . zu berechnen n × n Matrix zum Clustern und multidimensionalen Skalieren von n Mustersets.
 ist ein Maß auf einem messbaren Raum
ist ein Maß auf einem messbaren Raum  , dann definieren wir den Jaccard-Koeffizienten durch
, dann definieren wir den Jaccard-Koeffizienten durch


 oder
oder  , da diese Formeln in diesen Fällen nicht gut definiert sind.
, da diese Formeln in diesen Fällen nicht gut definiert sind.







 und
und  sind zwei Vektoren mit allen reellen
sind zwei Vektoren mit allen reellen  , dann ist ihr Jaccard-Ähnlichkeitskoeffizient (damals auch als Ruzicka-Ähnlichkeit bekannt) definiert als
, dann ist ihr Jaccard-Ähnlichkeitskoeffizient (damals auch als Ruzicka-Ähnlichkeit bekannt) definiert als


 und
und  sind zwei nicht-negativ messbare Funktionen auf einem messbaren Raum
sind zwei nicht-negativ messbare Funktionen auf einem messbaren Raum 
 und
und  sind punktweise Operatoren. Dann ist die Jackcard-Distanz
sind punktweise Operatoren. Dann ist die Jackcard-Distanz

 , wir haben
, wir haben  wo
wo  und
und  sind die charakteristischen Funktionen der entsprechenden Menge.
sind die charakteristischen Funktionen der entsprechenden Menge.
 . Es verallgemeinert den Jaccard-Index jedoch nicht auf Wahrscheinlichkeitsverteilungen, bei denen eine Menge einer einheitlichen Wahrscheinlichkeitsverteilung entspricht, dh
. Es verallgemeinert den Jaccard-Index jedoch nicht auf Wahrscheinlichkeitsverteilungen, bei denen eine Menge einer einheitlichen Wahrscheinlichkeitsverteilung entspricht, dh


 dann
dann



 , ist eine Metrik über Wahrscheinlichkeitsverteilungen und eine Pseudometrik über nicht-negativen Vektoren.
, ist eine Metrik über Wahrscheinlichkeitsverteilungen und eine Pseudometrik über nicht-negativen Vektoren.
 -simplex entspricht einer Wahrscheinlichkeitsverteilung auf
-simplex entspricht einer Wahrscheinlichkeitsverteilung auf  Elemente, weil die Einheit
Elemente, weil die Einheit  und
und  , wir möchten bauen
, wir möchten bauen  maximieren
maximieren ![{displaystyle Pr[X=Y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c35204086ef689f4c1ed3bbeedaa8a8ac942793) . Wenn wir uns nur zwei Verteilungen ansehen
. Wenn wir uns nur zwei Verteilungen ansehen  isoliert, das Höchste
isoliert, das Höchste  wo
wo  ist die Gesamtvariationsdistanz. Angenommen, es geht uns nicht nur um die Maximierung dieses bestimmten Paares, sondern wir möchten die Kollisionswahrscheinlichkeit eines beliebigen Paares maximieren. Man könnte unendlich viele Zufallsvariablen konstruieren, eine für jede Verteilung
ist die Gesamtvariationsdistanz. Angenommen, es geht uns nicht nur um die Maximierung dieses bestimmten Paares, sondern wir möchten die Kollisionswahrscheinlichkeit eines beliebigen Paares maximieren. Man könnte unendlich viele Zufallsvariablen konstruieren, eine für jede Verteilung  , und versuchen zu maximieren
, und versuchen zu maximieren  und diskrete Verteilungen
und diskrete Verteilungen ![{displaystyle Pr[G(x)=G(y)]>J_{mathcal{P}}(x,y)}”/></span> dann für einige <span class=](https://wikimedia.org/api/rest_v1/media/math/render/svg/d51bcb8456e58c7bfdc742dc68a54693ed5dfacf)
 wo
wo 

 auf einem Paar, ohne weniger Kollisionen zu erzielen als
auf einem Paar, ohne weniger Kollisionen zu erzielen als  ist der ichth bisschen x, und
ist der ichth bisschen x, und  sind bitweise und, oder Operatoren, dann ist das Ähnlichkeitsverhältnis
sind bitweise und, oder Operatoren, dann ist das Ähnlichkeitsverhältnis  ist
ist


 . Diese Funktion ist eine geeignete Distanzmetrik. “Tanimoto-Distanz” wird oft als richtige Distanzmetrik angegeben, wahrscheinlich wegen der Verwechslung mit der Jaccard-Distanz.
. Diese Funktion ist eine geeignete Distanzmetrik. “Tanimoto-Distanz” wird oft als richtige Distanzmetrik angegeben, wahrscheinlich wegen der Verwechslung mit der Jaccard-Distanz.



 behält die Dreiecksungleichung nicht bei und ist daher keine richtige Distanzmetrik, wohingegen
behält die Dreiecksungleichung nicht bei und ist daher keine richtige Distanzmetrik, wohingegen  so dass für jeden Vektor EIN in Betracht gezogen werden,
so dass für jeden Vektor EIN in Betracht gezogen werden,  Unter diesen Umständen ist die Funktion eine geeignete Distanzmetrik, und so bildet ein Satz von Vektoren, der von einem solchen Gewichtungsvektor bestimmt wird, einen metrischen Raum unter dieser Funktion.
Unter diesen Umständen ist die Funktion eine geeignete Distanzmetrik, und so bildet ein Satz von Vektoren, der von einem solchen Gewichtungsvektor bestimmt wird, einen metrischen Raum unter dieser Funktion.

Recent Comments