Diffie-Hellman-Schlüsselaustausch – Wikipedia

Verfahren zum Austausch von kryptografischen Schlüsseln

Beim Diffie-Hellman-Schlüsselaustauschschema erzeugt jede Partei ein öffentliches/privates Schlüsselpaar und verteilt den öffentlichen Schlüssel. Nachdem Alice und Bob eine authentische Kopie der öffentlichen Schlüssel des anderen erhalten haben, können sie offline ein gemeinsames Geheimnis berechnen. Das Shared Secret kann beispielsweise als Schlüssel für eine symmetrische Chiffre verwendet werden.

Diffie-Hellman-Schlüsselaustausch^{[nb 1]} ist eine Methode zum sicheren Austausch von kryptografischen Schlüsseln über einen öffentlichen Kanal und war eines der ersten Public-Key-Protokolle, wie es von Ralph Merkle konzipiert und nach Whitfield Diffie und Martin Hellman benannt wurde.^[1][2] DH ist eines der frühesten praktischen Beispiele für den Austausch öffentlicher Schlüssel, der im Bereich der Kryptographie implementiert wurde. 1976 von Diffie und Hellman veröffentlicht, ist dies die früheste öffentlich bekannte Arbeit, die die Idee eines privaten Schlüssels und eines entsprechenden öffentlichen Schlüssels vorschlug.

Herkömmlicherweise erforderte eine sichere verschlüsselte Kommunikation zwischen zwei Parteien, dass sie zuerst Schlüssel auf einem sicheren physischen Weg austauschen, wie z. B. Schlüssellisten auf Papier, die von einem vertrauenswürdigen Kurier transportiert werden. Das Diffie-Hellman-Schlüsselaustauschverfahren ermöglicht es zwei Parteien, die keine Vorkenntnisse voneinander haben, gemeinsam einen gemeinsamen geheimen Schlüssel über einen unsicheren Kanal zu erstellen. Dieser Schlüssel kann dann verwendet werden, um nachfolgende Kommunikationen unter Verwendung einer symmetrischen Schlüsselchiffre zu verschlüsseln.

Diffie-Hellman wird verwendet, um eine Vielzahl von Internetdiensten abzusichern. Untersuchungen, die im Oktober 2015 veröffentlicht wurden, legen jedoch nahe, dass die Parameter, die zu dieser Zeit für viele DH-Internetanwendungen verwendet werden, nicht stark genug sind, um eine Kompromittierung durch sehr gut finanzierte Angreifer, wie etwa die Sicherheitsdienste einiger Länder, zu verhindern.^[3]

Das Schema wurde 1976 von Whitfield Diffie und Martin Hellman veröffentlicht.^[2] 1997 wurde jedoch bekannt, dass James H. Ellis,^[4]Clifford Cocks und Malcolm J. Williamson vom britischen Nachrichtendienst GCHQ hatten bereits 1969 gezeigt^[5] wie eine Kryptografie mit öffentlichem Schlüssel erreicht werden könnte.^[6]

Obwohl die Diffie-Hellman-Schlüsselvereinbarung selbst ein nicht authentifiziertes Schlüsselvereinbarungsprotokoll ist, bietet sie die Grundlage für eine Vielzahl von authentifizierten Protokollen und wird verwendet, um in den kurzlebigen Modi von Transport Layer Security (je nach die Verschlüsselungssammlung).

Der Methode folgte kurz darauf RSA, eine Implementierung der Public-Key-Kryptographie mit asymmetrischen Algorithmen.

Abgelaufen US-Patent 4.200.770 von 1977 beschreibt den mittlerweile gemeinfreien Algorithmus. Es schreibt Hellman, Diffie und Merkle als Erfinder zu.

Im Jahr 2002 schlug Hellman vor, den Algorithmus zu nennen Diffie–Hellman–Merkle-Schlüsselaustausch in Anerkennung des Beitrags von Ralph Merkle zur Erfindung der Public-Key-Kryptographie (Hellman, 2002), schreibend:

Das System … ist seither als Diffie-Hellman-Schlüsselaustausch bekannt. Dieses System wurde zwar zum ersten Mal in einem Aufsatz von Diffie und mir beschrieben, es ist jedoch ein öffentliches Schlüsselverteilungssystem, ein von Merkle entwickeltes Konzept, und sollte daher “Diffie-Hellman-Merkle-Schlüsselaustausch” heißen, wenn Namen damit in Verbindung gebracht werden sollen . Ich hoffe, dass diese kleine Kanzel dabei helfen kann, Merkles gleichberechtigten Beitrag zur Erfindung der Kryptographie mit öffentlichen Schlüsseln anzuerkennen.^[7]

Beschreibung[edit]

Gesamtübersicht[edit]

Veranschaulichung des Konzepts hinter dem Diffie-Hellman-Schlüsselaustausch

Der Diffie-Hellman-Schlüsselaustausch erstellt ein gemeinsames Geheimnis zwischen zwei Parteien, das für die geheime Kommunikation zum Austausch von Daten über ein öffentliches Netzwerk verwendet werden kann. Eine Analogie veranschaulicht das Konzept des Austauschs öffentlicher Schlüssel durch die Verwendung von Farben anstelle von sehr großen Zahlen:

Der Prozess beginnt damit, dass sich die beiden Parteien, Alice und Bob, öffentlich auf eine willkürliche Startfarbe einigen, die nicht geheim gehalten werden muss (aber jedes Mal anders sein sollte .)^[3]). In diesem Beispiel ist die Farbe gelb. Außerdem wählt jeder eine geheime Farbe aus, die er für sich behält – in diesem Fall Rot und Blaugrün. Der entscheidende Teil des Prozesses besteht darin, dass Alice und Bob jeweils ihre eigene geheime Farbe mit ihrer gemeinsamen Farbe mischen, was zu orange-braunen bzw. hellblauen Mischungen führt, und dann die beiden gemischten Farben öffentlich austauschen. Schließlich mischt jeder von ihnen die Farbe, die er vom Partner erhalten hat, mit seiner eigenen privaten Farbe. Das Ergebnis ist eine endgültige Farbmischung (in diesem Fall gelb-braun), die mit der endgültigen Farbmischung des Partners identisch ist.

Wenn ein Dritter dem Austausch zuhörte, würde er nur die gemeinsame Farbe (Gelb) und die ersten Mischfarben (Orange-Tan und Hellblau) kennen, aber für diesen wäre es schwierig, die endgültige geheime Farbe (Gelb -Braun). Wenn man die Analogie auf einen realen Austausch zurückbringt, der große Zahlen anstelle von Farben verwendet, ist diese Bestimmung rechenintensiv. Selbst für moderne Supercomputer ist eine Berechnung in praktischer Zeit nicht möglich.

Kryptografische Erklärung[edit]

Die einfachste und originellste Implementierung^[2] des Protokolls verwendet die multiplikative Gruppe von ganzen Zahlen modulo P, wo P ist prim, und g ist eine primitive Wurzel modulo P. Diese beiden Werte werden auf diese Weise gewählt, um sicherzustellen, dass das resultierende gemeinsame Geheimnis jeden Wert von 1 bis annehmen kann P–1. Hier ist ein Beispiel für das Protokoll mit nicht geheimen Werten in Blau, und geheime Werte in rot.

1. Alice und Bob stimmen öffentlich zu, einen Modul zu verwenden P = 23 und Basis g = 5 (was eine primitive Wurzel modulo 23 ist).
2. Alice wählt eine geheime ganze Zahl ein = 4, dann sendet Bob EIN = g^ein mod P
3. Bob wählt eine geheime ganze Zahl B = 3, dann sendet Alice B = g^B mod P
4. Alice berechnet S = B^ein mod P
5. Bob rechnet S = EIN^B mod P
6. Alice und Bob teilen nun ein Geheimnis (die Zahl 18).

Sowohl Alice als auch Bob haben die gleichen Werte erreicht, da unter mod p,

${displaystyle {color {Blau}A}^{color {Red}b}{bmod {color {Blau}p}}={color {Blau}g}^{color {Red}ab} {bmod {color {Blau}p}}={color {Blau}g}^{color {Rot}ba}{bmod {color {Blau}p}}={color {Blau}B }^{color {Rot}a}{bmod {color {Blau}p}}}$

Genauer,

${displaystyle ({color {Blau}g}^{color {Rot}a}{bmod {color {Blau}p}})^{color {Rot}b}{bmod {color { Blau}p}}=({color {Blau}g}^{color {Rot}b}{bmod {color {Blau}p}})^{color {Rot}a}{bmod { color {Blau}p}}}$

Nur ein und B werden geheim gehalten. Alle anderen Werte – P, g, g^ein mod P, und g^B mod P – werden im Klartext gesendet. Die Stärke des Schemas liegt darin, dass g^ab mod P = g^ba mod P dauert extrem lange, um von jedem bekannten Algorithmus zu berechnen, nur aufgrund der Kenntnis von P, g, g^ein mod P, und g^B mod P. Sobald Alice und Bob das gemeinsame Geheimnis berechnet haben, können sie es als Verschlüsselungsschlüssel verwenden, der nur ihnen bekannt ist, um Nachrichten über denselben offenen Kommunikationskanal zu senden.

Natürlich viel größere Werte von ein, B, und P wäre notwendig, um dieses Beispiel sicher zu machen, da es nur 23 mögliche Ergebnisse von n mod 23. Wenn jedoch P eine Primzahl von mindestens 600 Ziffern ist, können selbst die schnellsten modernen Computer mit dem schnellsten bekannten Algorithmus nicht finden ein nur gegeben g, P und g^ein mod P. Ein solches Problem wird als diskretes Logarithmusproblem bezeichnet.^[3] Die Berechnung von g^ein mod P ist als modulare Exponentiation bekannt und kann auch für große Zahlen effizient durchgeführt werden. Beachten Sie, dass g muss überhaupt nicht groß sein und ist in der Praxis normalerweise eine kleine ganze Zahl (wie 2, 3, …).

Geheimhaltungstabelle[edit]

Die folgende Tabelle zeigt wer weiß was, wieder mit nicht geheimen Werten in Blau, und geheime Werte in rot. Hier ist Eve eine Lauscherin – sie beobachtet, was zwischen Alice und Bob gesendet wird, aber sie ändert den Inhalt ihrer Kommunikation nicht.

• g = öffentliche (prime) Basis, die Alice, Bob und Eve bekannt ist. g = 5
• P = öffentlicher (Prime-)Modul, Alice, Bob und Eve bekannt. P = 23
• ein = Alices privater Schlüssel, der nur Alice bekannt ist. ein = 6
• B = Bobs privater Schlüssel, der nur Bob bekannt ist. B = fünfzehn
• EIN = Alices öffentlicher Schlüssel, Alice, Bob und Eve bekannt. EIN = g^ein mod P = 8
• B = Bobs öffentlicher Schlüssel, der Alice, Bob und Eve bekannt ist. B = g^B mod P = 19

Jetzt S ist der gemeinsame geheime Schlüssel und ist sowohl Alice als auch Bob bekannt, aber nicht zu Eva. Beachten Sie, dass es für Eve nicht hilfreich ist, zu berechnen AB, was gleich ist g^{ein + B} mod P.

Hinweis: Es sollte für Alice schwierig sein, nach Bobs privatem Schlüssel oder für Bob nach Alices privatem Schlüssel zu suchen. Wenn es für Alice nicht schwierig ist, nach Bobs privatem Schlüssel zu suchen (oder umgekehrt), kann Eve einfach ihr eigenes privates / öffentliches Schlüsselpaar ersetzen, Bobs öffentlichen Schlüssel in ihren privaten Schlüssel stecken, einen gefälschten gemeinsamen geheimen Schlüssel erzeugen und nach auflösen Bobs privater Schlüssel (und verwenden Sie diesen, um nach dem gemeinsamen geheimen Schlüssel zu suchen. Eve kann versuchen, ein öffentliches / privates Schlüsselpaar zu wählen, das es ihr leicht macht, nach Bobs privatem Schlüssel zu suchen).

Eine weitere Demonstration von Diffie-Hellman (auch mit Zahlen, die für den praktischen Gebrauch zu klein sind) wird gegeben Hier.^[8]

Verallgemeinerung auf endliche zyklische Gruppen[edit]

Hier ist eine allgemeinere Beschreibung des Protokolls:^[9]

1. Alice und Bob einigen sich auf eine endliche zyklische Gruppe g der Ordnung n und ein erzeugendes Element g in g. (Dies geschieht normalerweise lange vor dem Rest des Protokolls; g wird davon ausgegangen, dass alle Angreifer bekannt sind.) Die Gruppe g wird multiplikativ geschrieben.
2. Alice wählt eine zufällige natürliche Zahl ein, wobei 1 ein < n, und sendet g^ein mod n zu Bob.
3. Bob wählt eine zufällige natürliche Zahl B, was auch 1 . ist B < n, und sendet g^B mod n zu Alice.
4. Alice berechnet (g^B mod n)^ein mod n.
5. Bob berechnet (g^ein mod n)^B mod n.

Sowohl Alice als auch Bob besitzen jetzt das Gruppenelement g^ab, der als gemeinsamer geheimer Schlüssel dienen kann. Die Gruppe g die Voraussetzung für eine sichere Kommunikation erfüllt, wenn kein effizienter Algorithmus zur Bestimmung von g^ab gegeben g, g^ein, und g^B.

Das Diffie-Hellman-Protokoll mit elliptischen Kurven ist beispielsweise eine Variante, die elliptische Kurven anstelle der multiplikativen Gruppe von ganzen Zahlen modulo n verwendet. Es wurden auch Varianten vorgeschlagen, die hyperelliptische Kurven verwenden. Der supersinguläre Isogenie-Schlüsselaustausch ist eine Diffie-Hellman-Variante, die gegen Quantencomputer sicher ist.

Betrieb mit mehr als zwei Parteien[edit]

Die Diffie-Hellman-Schlüsselvereinbarung ist nicht darauf beschränkt, einen Schlüssel auszuhandeln, der nur von zwei Teilnehmern geteilt wird. Beliebig viele Benutzer können an einer Vereinbarung teilnehmen, indem sie Iterationen des Vereinbarungsprotokolls durchführen und Zwischendaten austauschen (die selbst nicht geheim gehalten werden müssen). Alice, Bob und Carol könnten beispielsweise wie folgt an einer Diffie-Hellman-Vereinbarung teilnehmen, wobei alle Operationen als modulo . angenommen werden P:

1. Die Parteien einigen sich auf die Algorithmusparameter P und g.
2. Die Parteien generieren ihre privaten Schlüssel, genannt ein, B, und C.
3. Alice berechnet g^ein und schickt es an Bob.
4. Bob berechnet (g^ein)^B = g^ab und schickt es an Carol.
5. Carol berechnet (g^ab)^C = g^ABC und benutzt es als ihr Geheimnis.
6. Bob rechnet g^B und schickt es an Carol.
7. Carol berechnet (g^B)^C = g^bc und schickt es an Alice.
8. Alice berechnet (g^bc)^ein = g^bca = g^ABC und benutzt es als ihr Geheimnis.
9. Carol berechnet g^C und schickt es an Alice.
10. Alice berechnet (g^C)^ein = g^ca und schickt es an Bob.
11. Bob berechnet (g^ca)^B = g^Taxi = g^ABC und benutzt es als sein Geheimnis.

Ein Lauscher konnte sehen g^ein, g^B, g^C, g^ab, g^ac, und g^bc, kann jedoch keine Kombination davon verwenden, um effizient zu reproduzieren g^ABC.

Um diesen Mechanismus auf größere Gruppen auszudehnen, müssen zwei Grundprinzipien befolgt werden:

• Beginnend mit einem “leeren” Schlüssel bestehend nur aus g, wird das Geheimnis gemacht, indem der aktuelle Wert einmal in beliebiger Reihenfolge auf den privaten Exponenten jedes Teilnehmers erhöht wird (die erste solche Potenzierung ergibt den eigenen öffentlichen Schlüssel des Teilnehmers).
• Jeder Zwischenwert (bis zu n-1 angewendete Exponenten, wobei n ist die Anzahl der Teilnehmer in der Gruppe) kann öffentlich bekannt gegeben werden, aber der endgültige Wert (alles hatte) n Exponenten angewendet) stellt das gemeinsame Geheimnis dar und darf daher niemals öffentlich bekannt gegeben werden. Daher muss jeder Benutzer seine Kopie des Geheimnisses erhalten, indem er zuletzt seinen eigenen privaten Schlüssel anwendet (andernfalls hätte der letzte Mitwirkende keine Möglichkeit, seinem Empfänger den endgültigen Schlüssel zu übermitteln, da dieser letzte Mitwirkende den Schlüssel in den eigentlichen Schlüssel verwandelt hätte geheim, das die Gruppe schützen wollte).

Diese Prinzipien lassen verschiedene Optionen offen, um zu wählen, in welcher Reihenfolge die Teilnehmer zu den Schlüsseln beitragen. Die einfachste und naheliegendste Lösung ist die Anordnung der n Teilnehmer im Kreis und haben n Schlüssel rotieren im Kreis, bis schließlich jeder Schlüssel von allen beigesteuert wurde n Teilnehmer (Endung mit seinem Besitzer) und jeder Teilnehmer hat dazu beigetragen n Schlüssel (mit eigenen enden). Dies setzt jedoch voraus, dass jeder Teilnehmer n modulare Potenzen.

Durch die Wahl einer optimaleren Reihenfolge und die Tatsache, dass Schlüssel dupliziert werden können, ist es möglich, die Anzahl der von jedem Teilnehmer durchgeführten modularen Potenzierungen auf zu reduzieren Protokoll₂(n) + 1 mit einem Divide-and-Conquer-Ansatz, hier für acht Teilnehmer:

1. Die Teilnehmer A, B, C und D führen jeweils eine Potenzierung durch, was g^{A B C D}; dieser Wert wird an E, F, G und H gesendet. Im Gegenzug erhalten die Teilnehmer A, B, C und D g^{E f G H}.
2. Die Teilnehmer A und B führen jeweils eine Potenzierung durch, was g^efghab, die sie an C und D senden, während C und D dasselbe tun, was g^efghcd, die sie an A und B senden.
3. Teilnehmer A führt eine Potenzierung durch und ergibt g^efghcda, die es an B sendet; ebenso sendet B g^efghcdb zu A. C und D verfahren ähnlich.
4. Teilnehmer A führt eine letzte Potenzierung durch, die das Geheimnis ergibt g^efghcdba = g^{A B C D E F G H}, während B dasselbe tut, um zu erhalten g^efghcdab = g^{A B C D E F G H}; C und D verhalten sich wieder ähnlich.
5. Die Teilnehmer E bis H führen gleichzeitig die gleichen Operationen durch, indem sie g^{A B C D} als ihren Ausgangspunkt.

Sobald dieser Vorgang abgeschlossen ist, besitzen alle Teilnehmer das Geheimnis g^{A B C D E F G H}, aber jeder Teilnehmer hat nur vier modulare Exponentiationen durchgeführt, anstatt der acht, die durch eine einfache kreisförmige Anordnung impliziert werden.

Sicherheit[edit]

Das Protokoll gilt als abhörsicher, wenn g und g richtig gewählt sind. Insbesondere muss die Ordnung der Gruppe G groß sein, insbesondere wenn dieselbe Gruppe für große Verkehrsmengen verwendet wird. Der Lauscher muss das Diffie-Hellman-Problem lösen, um zu erhalten g^ab. Dies gilt derzeit als schwierig für Gruppen, deren Auftrag groß genug ist. Ein effizienter Algorithmus zur Lösung des Problems des diskreten Logarithmus würde die Berechnung vereinfachen ein oder B und lösen das Diffie-Hellman-Problem, wodurch dieses und viele andere Kryptosysteme mit öffentlichen Schlüsseln unsicher werden. Felder mit kleinen Eigenschaften können weniger sicher sein.^[10]

Die Reihenfolge von g sollte einen großen Primfaktor haben, um zu verhindern, dass der Pohlig-Hellman-Algorithmus verwendet wird, um ein oder B. Aus diesem Grund eine Sophie Germain prime Q wird manchmal verwendet, um zu berechnen P = 2Q + 1, eine sichere Primzahl genannt, da die Ordnung g ist dann nur durch 2 teilbar und Q. g wird dann manchmal ausgewählt, um die Bestellung zu generieren Q Untergruppe von g, eher, als g, damit das Legendre-Symbol von g^ein enthüllt nie das niederwertige Bit von ein. Ein Protokoll, das eine solche Auswahl verwendet, ist beispielsweise IKEv2.^[11]

g ist oft eine kleine ganze Zahl wie 2. Wegen der zufälligen Selbstreduzierbarkeit des Problems des diskreten Logarithmus ist ein kleines g ist genauso sicher wie jeder andere Generator derselben Gruppe.

Wenn Alice und Bob Zufallszahlengeneratoren verwenden, deren Ausgaben nicht vollständig zufällig sind und in gewissem Maße vorhergesagt werden können, ist es viel einfacher, zuzuhören.

In der ursprünglichen Beschreibung bietet der Diffie-Hellman-Austausch selbst keine Authentifizierung der kommunizierenden Parteien und ist daher anfällig für einen Man-in-the-Middle-Angriff. Mallory (ein aktiver Angreifer, der den Man-in-the-Middle-Angriff ausführt) kann zwei verschiedene Schlüsselaustausche einrichten, einen mit Alice und den anderen mit Bob, wodurch er sich effektiv als Alice zu Bob ausgibt und umgekehrt, sodass sie entschlüsseln und dann wieder zurückgeben kann -encrypt, die zwischen ihnen ausgetauschten Nachrichten. Beachten Sie, dass Mallory weiterhin in der Mitte sein muss und Nachrichten bei jeder Kommunikation zwischen Alice und Bob aktiv entschlüsselt und neu verschlüsselt. Wenn sie jemals abwesend ist, wird ihre vorherige Anwesenheit Alice und Bob offenbart. Sie werden wissen, dass alle ihre privaten Gespräche von jemandem im Kanal abgefangen und entschlüsselt wurden. In den meisten Fällen wird es ihnen nicht helfen, Mallorys privaten Schlüssel zu erhalten, selbst wenn sie denselben Schlüssel für beide Börsen verwendet hat.

Um diese Art von Angriff zu verhindern, wird im Allgemeinen ein Verfahren benötigt, um die kommunizierenden Parteien untereinander zu authentifizieren. Stattdessen können Varianten von Diffie-Hellman, wie das STS-Protokoll, verwendet werden, um diese Arten von Angriffen zu vermeiden.

Praktische Angriffe auf den Internetverkehr[edit]

Der Zahlenfeldsiebalgorithmus, der im Allgemeinen der effektivste bei der Lösung des Problems des diskreten Logarithmus ist, besteht aus vier Rechenschritten. Die ersten drei Schritte hängen nur von der Ordnung der Gruppe G ab, nicht von der konkreten Zahl, deren endlicher Logarithmus gewünscht wird.^[12] Es stellt sich heraus, dass ein Großteil des Internetverkehrs eine von einer Handvoll Gruppen verwendet, die eine Größenordnung von 1024 Bit oder weniger haben.^[3] Durch die Vorberechnung der ersten drei Schritte des Zahlenfeldsiebs für die gängigsten Gruppen muss ein Angreifer nur den letzten Schritt ausführen, der viel weniger rechenintensiv als die ersten drei Schritte ist, um einen bestimmten Logarithmus zu erhalten. Der Logjam-Angriff nutzte diese Schwachstelle, um eine Vielzahl von Internetdiensten zu kompromittieren, die die Verwendung von Gruppen ermöglichten, deren Reihenfolge eine 512-Bit-Primzahl war, sogenannte Export-Grade. Die Autoren benötigten mehrere tausend CPU-Kerne für eine Woche, um Daten für einen einzelnen 512-Bit-Prime vorzurechnen. Danach konnten einzelne Logarithmen mit zwei 18-Kern Intel Xeon CPUs in etwa einer Minute gelöst werden.^[3]

Wie von den Autoren des Logjam-Angriffs geschätzt, würde die viel schwierigere Vorberechnung, die zur Lösung des diskreten Log-Problems für eine 1024-Bit-Primzahl erforderlich ist, in der Größenordnung von 100 Millionen US-Dollar kosten, was weit im Budget eines großen nationalen Geheimdienstes wie der US-amerikanische National Security Agency (NSA). Die Autoren von Logjam spekulieren, dass Vorberechnungen gegen weit verbreitete 1024-Bit-DH-Primzahlen hinter den Behauptungen in durchgesickerten NSA-Dokumenten stehen, dass die NSA in der Lage ist, einen Großteil der aktuellen Kryptographie zu knacken.^[3]

Um diese Schwachstellen zu vermeiden, empfehlen die Logjam-Autoren die Verwendung der elliptischen Kurvenkryptographie, für die kein ähnlicher Angriff bekannt ist. Andernfalls empfehlen sie, dass die Bestellung, P, der Diffie-Hellman-Gruppe sollte mindestens 2048 Bit betragen. Sie schätzen, dass die für eine 2048-Bit-Primzahl erforderliche Vorberechnung 10 . beträgt⁹ Mal schwieriger als bei 1024-Bit-Primzahlen.^[3]

Andere Verwendungen[edit]

Verschlüsselung[edit]

Verschlüsselungsschemata mit öffentlichem Schlüssel basierend auf dem Diffie-Hellman-Schlüsselaustausch wurden vorgeschlagen. Das erste derartige Schema ist die ElGamal-Verschlüsselung. Eine modernere Variante ist das Integrated Encryption Scheme.

Weiterleitungsgeheimnis[edit]

Protokolle, die Forward Secrecy erreichen, generieren für jede Sitzung neue Schlüsselpaare und verwerfen sie am Ende der Sitzung. Der Diffie-Hellman-Schlüsselaustausch ist aufgrund seiner schnellen Schlüsselgenerierung eine häufige Wahl für solche Protokolle.

Passwort-authentifizierte Schlüsselvereinbarung[edit]

Wenn Alice und Bob ein Passwort teilen, können sie eine Form von Diffie-Hellman (Passwortauthentifizierte Schlüsselvereinbarung) verwenden, um Man-in-the-Middle-Angriffe zu verhindern. Ein einfaches Schema besteht darin, den Hash von zu vergleichen S mit dem unabhängig berechneten Passwort an beiden Enden des Kanals verkettet. Ein Merkmal dieser Schemata besteht darin, dass ein Angreifer bei jeder Iteration mit der anderen Partei nur ein bestimmtes Passwort testen kann, sodass das System mit relativ schwachen Passwörtern eine gute Sicherheit bietet. Dieser Ansatz ist in der ITU-T-Empfehlung X.1035 beschrieben, die vom G.hn-Heimnetzwerkstandard verwendet wird.

Ein Beispiel für ein solches Protokoll ist das Secure Remote Password-Protokoll.

Öffentlicher Schlüssel[edit]

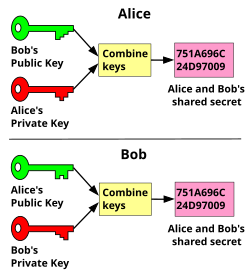
Es ist auch möglich, Diffie-Hellman als Teil einer Infrastruktur mit öffentlichem Schlüssel zu verwenden, sodass Bob eine Nachricht so verschlüsseln kann, dass nur Alice sie entschlüsseln kann, ohne dass zuvor eine Kommunikation zwischen ihnen besteht, außer dass Bob vertrauenswürdige Kenntnis von Alices öffentlichem Schlüssel hat . Alices öffentlicher Schlüssel ist

. Um ihr eine Nachricht zu senden, wählt Bob eine zufällige B und schickt dann Alice

(unverschlüsselt) zusammen mit der mit symmetrischem Schlüssel verschlüsselten Nachricht

. Nur Alice kann den symmetrischen Schlüssel ermitteln und damit die Nachricht entschlüsseln, da nur sie ein (der private Schlüssel). Ein Pre-Shared Public Key verhindert zudem Man-in-the-Middle-Angriffe.

In der Praxis wird Diffie-Hellman auf diese Weise nicht verwendet, da RSA der dominierende Public-Key-Algorithmus ist. Dies hat hauptsächlich historische und kommerzielle Gründe,^{[citation needed]} nämlich, dass RSA Security eine Zertifizierungsstelle für die Schlüsselsignierung erstellt hat, die zu Verisign wurde. Diffie-Hellman kann, wie oben ausgeführt, nicht direkt zum Signieren von Zertifikaten verwendet werden. Die Signaturalgorithmen ElGamal und DSA sind jedoch mathematisch damit verwandt, ebenso wie MQV, STS und die IKE-Komponente der IPsec-Protokollsuite zur Absicherung der Internetprotokoll-Kommunikation.

Siehe auch[edit]

Verweise[edit]

Allgemeine Referenzen[edit]

• Gollmann, Dieter (2011). Computersicherheit (2. Aufl.). West Sussex, England: John Wiley & Sons, Ltd. ISBN 978-0470741153.
• Williamson, Malcolm J. (21. Januar 1974). Nicht geheime Verschlüsselung mit einem endlichen Feld (PDF) (Technischer Bericht). Sicherheitsgruppe für Kommunikationselektronik. Abgerufen 2017-03-22.
• Williamson, Malcolm J. (10. August 1976). Gedanken zur billigeren, nicht geheimen Verschlüsselung (PDF) (Technischer Bericht). Sicherheitsgruppe für Kommunikationselektronik. Abgerufen 2015-08-25.
• Die Geschichte der nicht geheimen Verschlüsselung JH Ellis 1987 (28K PDF-Datei) (HTML-Version)
• Die ersten zehn Jahre der Public-Key-Kryptografie Whitfield Diffie, Proceedings of the IEEE, vol. 76, Nr. 5, Mai 1988, S.: 560–577 (1,9 MB PDF-Datei)
• Menez, Alfred; van Oorschot, Paul; Vanstone, Scott (1997). Handbuch der Angewandten Kryptographie Boca Raton, Florida: CRC-Presse. ISBN 0-8493-8523-7. (Online verfügbar)
• Singh, Simon (1999) Das Codebuch: die Evolution der Geheimhaltung von Mary Queen of Scots zur Quantenkryptographie New York: Doppeltag ISBN 0-385-49531-5
• Ein Überblick über die Kryptografie mit öffentlichen Schlüsseln Martin E. Hellman, IEEE Communications Magazine, Mai 2002, S. 42–49. (123kB PDF-Datei)

Externe Links[edit]