Tetraeder – Wikipedia

Regelmäßiges Tetraeder, ein Platonischer Körper
Art der Seitenflächen	gleichseitige Dreiecke
Anzahl der Flächen	4
Anzahl der Ecken	4
Anzahl der Kanten	6
Schläfli-Symbol	{3,3}
dual zu	Tetraeder
Körpernetz im Bild eins von zwei möglichen Netzen
Anzahl verschiedener Netze	2
Anzahl Kanten in einer Ecke	3
Anzahl Ecken einer Fläche	3

Das (auch, vor allem süddeutsch, der) Tetraeder [tetraˈeːdɐ] (von altgriechisch τετρα- tetra- „vier“ und ἕδρα hédra „Sitz“, „Sessel“, „Gesäß“ bzw. übertragen „Seitenfläche“), auch Vierflächner oder Vierflach, ist ein Körper mit vier dreieckigen Seitenflächen. Es ist das einzige konvexe Polyeder (Vielflach, Vielflächner) mit vier Flächen.

Das Wort wird jedoch nur selten in dieser allgemeinen Bedeutung gebraucht. Meist ist mit Tetraeder das regelmäßige Tetraeder mit gleichseitigen Dreiecken als Seitenflächen, das ein platonischer Körper ist, gemeint.

Das allgemeine Tetraeder wird je nach Symmetrie als dreiseitige Pyramide, Dreieckpyramide,^[1]Disphenoid oder dreidimensionales Simplex bezeichnet.

Das regelmäßige Tetraeder (reguläre Tetraeder) ist einer der fünf platonischen Körper, genauer ein Polyeder mit

Das regelmäßige Tetraeder ist auch eine gleichseitige dreiseitige Pyramide mit einem gleichseitigen Dreieck als Grundfläche.

Symmetrie[Bearbeiten | Quelltext bearbeiten]

Wegen seiner hohen Symmetrie – alle Ecken, Kanten und Flächen sind untereinander gleichartig – ist das regelmäßige Tetraeder ein reguläres Polyeder. Es hat

Insgesamt hat die Symmetriegruppe des Tetraeders – die Tetraedergruppe – 24 Elemente. Sie ist die symmetrische Gruppe S₄ (die Punktgruppe T_d nach Schoenflies bzw. 43m nach Hermann-Mauguin) und bewirkt alle 4! = 24 Permutationen der Ecken bzw. der Seitenflächen. Sie ist eine Untergruppe der Oktaedergruppe oder Würfelgruppe.

Im Einzelnen gehören zur Tetraedergruppe

sowie

• 12 ungerade Permutationen. Diese erhält man, indem man nach jeder der 12 geraden Permutationen noch die Spiegelung an einer festen Symmetrieebene durchführt. 6 davon lassen sich auch als eine reine Ebenenspiegelung beschreiben, die anderen sechs als Drehspiegelungen von Drehung um 90° um eine Achse, die durch die Mittelpunkte zweier gegenüberliegender Kanten verläuft, und Spiegelung an der zu dieser Achse senkrechten Ebene, die den Mittelpunkt zwischen den beiden gegenüberliegenden Kanten beinhaltet.

Die geraden Permutationen bilden eine Untergruppe der Tetraedergruppe, die so genannte alternierende Gruppe

${displaystyle A_{4}}$

(die Punktgruppe T bzw. 23). Manchmal wird der Begriff Tetraedergruppe auch nur für diese unter Ausschluss der Spiegelungen verwendet.

Das Tetraeder ist der einzige platonische Körper, der nicht punktsymmetrisch ist und bei dem jede Ecke einer Fläche gegenüberliegt.

Weitere Eigenschaften[Bearbeiten | Quelltext bearbeiten]

Verhältnis zu Oktaeder, Würfel, archimedischen Körpern[Bearbeiten | Quelltext bearbeiten]

Durch Verbinden der Flächenmittelpunkte erhält man wieder ein Tetraeder (siehe Abbildung). Man sagt deshalb: Das Tetraeder ist zu sich selbst dual, kurz: selbst-dual. Die Seitenlänge des einbeschriebenen Tetraeders beträgt ein Drittel der ursprünglichen Seitenlänge.

Mit Hilfe dieser beiden Tetraeder können Körper konstruiert werden, die ebenfalls die Tetraedergruppe als Symmetriegruppe haben. So erhält man zum Beispiel

Siehe dazu auch das Beispiel weiter unten.

Umgebender Würfel[Bearbeiten | Quelltext bearbeiten]

Das Tetraeder kann in einen Würfel (Hexaeder) so einbeschrieben werden, dass seine Ecken zugleich Würfelecken und seine Kanten Diagonalen der Würfelflächen sind (siehe Abbildung). Das Volumen dieses Würfels ist das Dreifache des Tetraedervolumens. Die 8 Ecken des Würfels bilden zwei disjunkte Mengen von je vier Ecken, die den beiden möglichen Lagen des Tetraeders entsprechen.

Tetraeder umschreibt Oktaeder[Bearbeiten | Quelltext bearbeiten]

Wird ein Oktaeder von einem Tetraeder umschrieben, sind die sechs Ecken des Oktaeders die Mittelpunkte der sechs Tetraederkanten und liegen vier der acht Oktaederflächen in den Seitenflächen eines der beiden möglichen Tetraeder.^[2]

Winkel[Bearbeiten | Quelltext bearbeiten]

Der Flächenwinkel zwischen zwei Seitenflächen des regelmäßigen Tetraeders

${displaystyle alpha }$

 beträgt 70,53° (

${displaystyle textstyle cos alpha ={frac {1}{3}}}$

).

Jede Kante bildet mit der Fläche, auf der sie steht, einen Winkel

${displaystyle beta }$

 von 54,74° (

${displaystyle textstyle tan beta ={sqrt {2}}}$

).

Die Verbindungsstrecken zwischen dem Tetraedermittelpunkt und zwei Ecken schließen jeweils einen Winkel von

${displaystyle tau }$

  = 109,47° (

${displaystyle textstyle cos tau ={-{frac {1}{3}}}}$

) ein.

Dieser wird als Tetraederwinkel bezeichnet, und er spielt eine wichtige Rolle in der Chemie, beispielsweise bei der Geometrie des Methan-Moleküls.

Die Größen der angegebenen Winkel lassen sich durch Anwendung trigonometrischer Funktionen ermitteln (siehe stumpfer Winkel). Man betrachtet dazu die Schnittfigur des Tetraeders (siehe Abbildung) mit einer seiner sechs Symmetrieebenen.

Querschnitt[Bearbeiten | Quelltext bearbeiten]

Das regelmäßige Tetraeder kann so in zwei Teile geschnitten werden, dass die Schnittfläche ein Quadrat ist. Die entstehenden Teile des Tetraeders sind kongruent zueinander.

Liegt die Schnittebene durch ein regelmäßiges Tetraeder parallel zu einer der vier Seitenflächen, dann ergibt der Querschnitt ein gleichseitiges Dreieck.

Liegt die Schnittebene durch ein regelmäßiges Tetraeder parallel zu zwei gegenüberliegenden Kanten, dann ergibt der Querschnitt ein Rechteck. Hat die Schnittebene zusätzlich noch von diesen beiden Kanten den gleichen Abstand, also teilt sie die übrigen vier Kanten genau zur Hälfte, dann ist das Schnittbild ein Quadrat. Das Quadrat hat eine Kantenlänge, die genau halb so lang ist wie die Länge einer Kante des Tetraeders.

Beispiel[Bearbeiten | Quelltext bearbeiten]

Die Einbettung des Tetraeders in einen Würfel bietet eine einfache Möglichkeit, ein regelmäßiges Tetraeder zu konstruieren. Bezeichnen wir die Eckpunkte des Würfels an der Basis mit

${displaystyle A,B,C}$

und

${displaystyle D}$

sowie die darüberliegenden Eckpunkte mit

${displaystyle E,F,G}$

und

${displaystyle H}$

, so bilden

${displaystyle A,C,F}$

und

${displaystyle H}$

sowie

${displaystyle B,D,E}$

und

${displaystyle G}$

jeweils die Ecken eines Tetraeders. Betrachtet man z. B. in einem räumlichen kartesischen Koordinatensystem den Würfel, dessen Ecken die Koordinaten

${displaystyle +1}$

und

${displaystyle -1}$

haben, so erhält man für das erste Tetraeder die Ecken

• 
  ${displaystyle A(1,1,-1),C(-1,-1,-1),F(-1,1,1)}$

  und

  ${displaystyle H(1,-1,1)}$

  .

Die Kanten sind:

${displaystyle AC,AF,AH,CF,CH}$

und

${displaystyle FH}$

. Die Seitenflächen sind die Dreiecke

${displaystyle ACF,ACH,AFH}$

und

${displaystyle CFH}$

.

Das zweite Tetraeder hat die Ecken

• 
  ${displaystyle B(-1,1,-1),D(1,-1,-1),E(1,1,1)}$

  und

  ${displaystyle G(-1,-1,1)}$

  .

Die dreidimensionale Schnittmenge dieser beiden Tetraeder ist das von den Punkten

${displaystyle (1,0,0),(-1,0,0),(0,1,0)(0,-1,0),(0,0,1)}$

und

${displaystyle (0,0,-1)}$

bestimmte Oktaeder. Ihre Vereinigungsmenge ist das Sterntetraeder. Seine konvexe Hülle ist daher der Würfel.

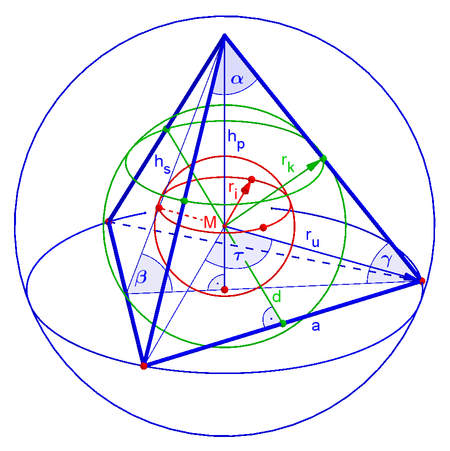
Formeln[Bearbeiten | Quelltext bearbeiten]

Größen eines regulären Tetraeders mit Kantenlänge a
Volumen	${displaystyle V={frac {a^{3}}{12}}cdot {sqrt {2}}approx 0{,}118cdot a^{3}}$	ohne Raumwinkel ${displaystyle Omega }$ in den Ecken
Oberflächeninhalt	${displaystyle A_{O}=a^{2}cdot {sqrt {3}}approx 1{,}732cdot a^{2}}$
Umkugelradius	${displaystyle r_{u}=3cdot r_{i}={frac {a}{4}}cdot {sqrt {6}}approx 0{,}612cdot a}$ [3]
Kantenkugelradius	${displaystyle r_{k}={frac {a}{4}}cdot {sqrt {2}}approx 0{,}354cdot a}$ [4]
Inkugelradius	${displaystyle r_{i}={frac {a}{12}}cdot {sqrt {6}}approx 0{,}204cdot a}$ [5]
Pyramidenhöhe	${displaystyle h_{p}=r_{i}+r_{u}={frac {a}{3}}cdot {sqrt {6}}approx 0{,}816cdot a}$
Kantenabstand	${displaystyle d=2cdot r_{k}={frac {a}{2}}cdot {sqrt {2}}approx 0{,}707cdot a}$
Verhältnis von Volumen zu Umkugelvolumen	${displaystyle {frac {V}{V_{UK}}}={frac {2cdot {sqrt {3}}}{9cdot pi }}approx 0{,}123}$
Innenwinkel des gleichseitigen Dreiecks	${displaystyle alpha =60^{circ }}$
Winkel zwischen benachbarten Flächen	${displaystyle beta =arccos left({frac {1}{3}}right)}$   ${displaystyle approx 70^{circ };31^{prime };44^{prime prime }}$
Winkel zwischen Kante und Fläche	${displaystyle gamma =arctan left({sqrt {2}}right)}$   ${displaystyle approx 54^{circ };44^{prime };8^{prime prime }}$
Tetraederwinkel	${displaystyle tau =arccos left(-{frac {1}{3}}right)approx 109^{circ };28^{prime };16^{prime prime }}$
Raumwinkel in den Ecken	${displaystyle Omega =arccos left({frac {23}{27}}right)approx 0{,}5512856;mathrm {sr} }$
Sphärizität	${displaystyle Psi ={sqrt[{3}]{frac {pi }{6{sqrt {3}}}}}approx 0{,}671}$

Berechnung des regelmäßigen Tetraeders[Bearbeiten | Quelltext bearbeiten]

Volumen[Bearbeiten | Quelltext bearbeiten]

Für Pyramiden und somit für das Tetraeder gilt

${displaystyle V={frac {1}{3}}cdot A_{G}cdot h_{p},}$

darin ist die Grundfläche (gleichseitiges Dreieck)

${displaystyle A_{G}={frac {sqrt {3}}{4}}cdot a^{2}}$

und die Höhe der Pyramide

${displaystyle h_{p}={frac {a}{3}}cdot {sqrt {6}},}$

mit eingesetzten Variablen wird

${displaystyle {begin{aligned}V&={frac {1}{3}}cdot {frac {sqrt {3}}{4}}cdot a^{2}cdot {frac {a}{3}}cdot {sqrt {6}}={frac {1}{3}}cdot {frac {1}{4}}cdot {frac {1}{3}}cdot {sqrt {3}}cdot {sqrt {6}}cdot a^{3}={frac {1}{12}}cdot {frac {1}{3}}cdot {sqrt {3}}cdot {sqrt {6}}cdot a^{3}\&={frac {a^{3}}{12}}cdot {sqrt {2}}approx 0{,}118cdot a^{3}end{aligned}}}$

Das Volumen kann auch als Differenz eines dem regelmäßigen Tetraeder umbeschriebenen Würfels mit der Kantenlänge

${displaystyle {tfrac {a}{sqrt {2}}}}$

und 4 nicht regelmäßigen Tetraedern, die jeweils eine gemeinsame rechtwinklige Ecke mit diesem Würfel haben, berechnet werden. Die 4 Ecken des Tetraeders stimmen mit 4 alternierenden Ecken dieses Würfels überein. Die 4 nicht regelmäßigen Tetraeder haben jeweils 1 Seitenfläche mit dem regelmäßigen Tetraeder gemeinsam und außerdem 3 rechtwinklige und gleichschenklige Dreiecke mit der Hypotenusenlänge

${displaystyle a}$

und der Kathetenlänge

${displaystyle {tfrac {a}{sqrt {2}}}}$

als Seitenflächen. Diese Kathetenlänge kann daher als Höhe für die Berechnung des Volumens verwendet werden.

Es ergibt sich logischerweise dasselbe Volumen

${displaystyle {begin{aligned}V&=left({frac {a}{sqrt {2}}}right)^{3}-4cdot {frac {1}{3}}cdot {frac {1}{2}}cdot left({frac {a}{sqrt {2}}}right)^{2}cdot {frac {a}{sqrt {2}}}=left(1-4cdot {frac {1}{3}}cdot {frac {1}{2}}right)cdot left({frac {a}{sqrt {2}}}right)^{3}={frac {1}{3}}cdot {frac {a^{3}}{2cdot {sqrt {2}}}}\&={frac {a^{3}}{12}}cdot {sqrt {2}}approx 0{,}118cdot a^{3}end{aligned}}}$

Oberflächeninhalt[Bearbeiten | Quelltext bearbeiten]

Für den Oberflächeninhalt

${displaystyle A_{O}}$

des Tetraeders (vier gleichseitige Dreiecke) gilt

${displaystyle A_{O}=4cdot {frac {sqrt {3}}{4}}cdot a^{2}=a^{2}cdot {sqrt {3}}.}$

Pyramidenhöhe[Bearbeiten | Quelltext bearbeiten]

Die Höhe der Pyramide

${displaystyle h_{p}}$

ist mithilfe des folgenden rechtwinkligen Dreiecks bestimmbar.

Die Seitenlängen dieses Dreiecks sind (siehe Bild in Formeln):
Seitenhöhe

${displaystyle h_{s}}$

als Hypotenuse, Pyramidenhöhe

${displaystyle h_{p}}$

als große Kathete und ein Drittel der Seitenhöhe

${textstyle {frac {1}{3}}cdot h_{s}}$

als kleine Kathete. Dieser Wert ist durch die Position des Fußpunktes von

${displaystyle h_{p}}$

(Flächenschwerpunkt der Grundfläche) bestimmt. Der geometrische Schwerpunkt teilt die Höhe des Dreiecks im Verhältnis 2:1.

Für die Höhe

${displaystyle h_{s}}$

des gleichseitigen Dreiecks gilt

 

${displaystyle h_{s}={frac {sqrt {3}}{2}}cdot a}$

und nach dem Satz des Pythagoras

${displaystyle {begin{aligned};h_{p}^{2}&=h_{s}^{2}-left({frac {1}{3}}cdot h_{s}right)^{2}=h_{s}^{2}-{frac {1}{9}}cdot h_{s}^{2}={frac {8}{9}}cdot h_{s}^{2};Rightarrow \&={frac {8}{9}}cdot {frac {3}{4}}cdot a^{2}={frac {2}{3}}cdot a^{2}Rightarrow \h_{p}&={sqrt {{frac {2}{3}}cdot a^{2}}}={sqrt {frac {2}{3}}}cdot a={frac {a}{3}}cdot {sqrt {6}}.;end{aligned}}}$

Winkel zwischen benachbarten Flächen[Bearbeiten | Quelltext bearbeiten]

Dieser Winkel, bezeichnet mit

${displaystyle beta }$

, hat seinen Scheitel an einer Kante des Tetraeders. Er ist mithilfe des folgenden rechtwinkligen Dreiecks bestimmbar.

Die Seitenlängen dieses Dreiecks sind (siehe Bild in Formeln):
Seitenhöhe

${displaystyle h_{s}}$

als Hypotenuse, Pyramidenhöhe

${displaystyle h_{p}}$

als große Kathete und ein Teil der Seitenhöhe

${textstyle {frac {1}{3}}cdot h_{s}}$

(siehe hierzu Höhen) als kleine Kathete.

Nach dem satz des Pythagoras gilt

${displaystyle {begin{aligned};cos beta &={frac {frac {h_{s}}{3}}{h_{s}}}={frac {{frac {1}{3}}left({frac {sqrt {3}}{2}}right)cdot a}{{frac {sqrt {3}}{2}}cdot a}}={frac {1}{3}}Rightarrow \beta &=arccos left({frac {1}{3}}right)approx 70^{circ };31^{prime };44^{prime prime };end{aligned}}}$

Winkel zwischen Kante und Fläche[Bearbeiten | Quelltext bearbeiten]

Dieser Winkel, bezeichnet mit

${displaystyle gamma }$

, hat seinen Scheitel an einer Ecke des Tetraeders. Winkel

${displaystyle gamma }$

ist mithilfe des folgenden rechtwinkligen Dreiecks bestimmbar.

Die Seitenlängen dieses Dreiecks sind (siehe Bild in Formeln): Pyramidenkante

${displaystyle a}$

als Hypotenuse, Pyramidenhöhe

${displaystyle h_{p}}$

als große Kathete und ein Teil der Seitenhöhe

${textstyle {frac {2}{3}}cdot h_{s}}$

(siehe hierzu Höhen) als kleine Kathete.

Für den Winkel

${displaystyle gamma }$

gilt

${displaystyle {begin{aligned};tan gamma &={frac {h_{p}}{{frac {2}{3}}cdot h_{s}}}={frac {{frac {a}{3}}cdot {sqrt {6}}}{{frac {2}{3}}cdot {frac {sqrt {3}}{2}}cdot a}}={frac {{frac {1}{3}}cdot {sqrt {6}}}{{frac {1}{3}}cdot {sqrt {3}}}}={sqrt {2}}Rightarrow \;\gamma &=arctan left({sqrt {2}}right)approx 54^{circ };44^{prime };8^{prime prime };end{aligned}}}$

Tetraederwinkel[Bearbeiten | Quelltext bearbeiten]

Dieser Winkel, bezeichnet mit

${displaystyle tau }$

, hat seinen Scheitel am Mittelpunkt des Tetraeders. Der Winkel

${displaystyle tau }$

ist mithilfe des folgenden rechtwinkligen Dreiecks bestimmbar.

Die Seitenlängen dieses Dreiecks sind (siehe Bild in Formeln): Umkugelradius

${displaystyle r_{u}}$

als Hypotenuse, halbe Kantenlänge

${textstyle {frac {1}{2}}cdot a}$

als große Kathete und der halbe Kantenabstand

${textstyle {frac {1}{2}}cdot d}$

als kleine Kathete.

Für den Winkel

${displaystyle tau }$

gilt

${displaystyle {begin{aligned};cos {frac {tau }{2}}&={frac {frac {d}{2}}{r_{u}}}={frac {frac {{frac {a}{2}}cdot {sqrt {2}}}{2}}{{frac {a}{4}}cdot {sqrt {6}}}}={frac {{frac {a}{4}}cdot {sqrt {2}}}{{frac {a}{4}}cdot {sqrt {6}}}}={frac {1}{sqrt {3}}}Rightarrow \cos tau &=cos left(arccos left({frac {1}{sqrt {3}}}right)cdot 2right)=-{frac {1}{3}}Rightarrow \tau &=arccos left(-{frac {1}{3}}right)approx 109^{circ };28^{prime };16^{prime prime }approx 1{,}910633236249,mathrm {rad} end{aligned}}}$

Raumwinkel in den Ecken[Bearbeiten | Quelltext bearbeiten]

Einen Lösungsweg für den Raumwinkel

${displaystyle Omega }$

zeigt die folgende Formel, beschrieben in Platonischer Körper

${displaystyle Omega =2pi -2ncdot arcsin left(cos left({frac {pi }{n}}right)cdot {sqrt {tan ^{2}left({frac {pi }{n}}right)-tan ^{2}left({frac {alpha }{2}}right)}}right)}$

^[6]

Mit der Anzahl der Kanten/Flächen an einer Ecke

${displaystyle {n=3}}$

und dem Innenwinkel des gleichseitigen Dreiecks

${displaystyle {a=60^{circ }}}$

gilt

${displaystyle {begin{aligned}{mathsf {(1)}};Omega &=2pi -2cdot 3cdot arcsin left(cos left({frac {pi }{3}}right)cdot {sqrt {tan ^{2}left({frac {pi }{3}}right)-tan ^{2}left({frac {60^{circ }}{2}}right)}}right)Rightarrow \&=2pi -6cdot arcsin left({sqrt {frac {2}{3}}}right)approx 0{,}551285598;mathrm {sr} \end{aligned}}}$

wegen

${displaystyle cos(arcsin x)={sqrt {1-x^{2}}}}$

wird damit

${displaystyle {begin{aligned}{mathsf {(2)}};cos(arcsin x)&={sqrt {1-left({sqrt {frac {2}{3}}}right)^{2}}}={frac {1}{sqrt {3}}}Rightarrow \end{aligned}}}$

eingesetzt

${displaystyle {mathsf {(2)}}}$

in

${displaystyle {mathsf {(1)}}}$

und umgeformt

${displaystyle {begin{aligned}{mathsf {(3)}};Omega &=2pi -6cdot arccos left({frac {1}{sqrt {3}}}right)approx 0{,}551285598;mathrm {sr} ;end{aligned}}}$

Vereinfachung^[7]

${displaystyle {begin{aligned}{mathsf {(4)}};cos Omega &=cos left(2pi -6cdot arccos left({frac {1}{sqrt {3}}}right)right)={frac {23}{27}}Rightarrow \end{aligned}}}$

${displaystyle {begin{aligned}{mathsf {(5)}};Omega &=arccos left({frac {23}{27}}right)approx 0{,}551285598;mathrm {sr} .;end{aligned}}}$

Netze des regelmäßigen Tetraeders[Bearbeiten | Quelltext bearbeiten]

Das Tetraeder hat zwei Netze (siehe Abbildungen)^[8] Das heißt, es gibt zwei verschiedene Möglichkeiten, ein hohles Tetraeder durch Aufschneiden von 3 Kanten aufzuklappen und in der Ebene auszubreiten. Die anderen 3 Kanten verbinden jeweils die 4 gleichseitigen Dreiecke des Netzes. Um ein Tetraeder so zu färben, dass keine benachbarten Flächen dieselbe Farbe haben, braucht man 4 Farben.

• 
• 

Graphen, duale Graphen, Zyklen, Färbungen[Bearbeiten | Quelltext bearbeiten]

Das Tetraeder hat einen ihm zugeordneten ungerichteten planaren Graphen mit 4 Knoten, 6 Kanten und 4 Gebieten. Dies ist der vollständige Graph K₄. Er ist 3-regulär, d. h. von jedem Knoten gehen 3 Kanten aus, sodass der Grad für alle Knoten gleich 3 ist. Bei planaren Graphen ist die genaue geometrische Anordnung der Knoten unwesentlich. Wichtig ist allerdings, dass sich die Kanten nicht schneiden müssen. Die Knoten dieses Tetraedergraphen entsprechen den Ecken des Tetraeders.

Die Knoten des Tetraedergraphen können mit 4 Farben so gefärbt werden, dass benachbarte Knoten immer unterschiedlich gefärbt sind, denn alle Knoten sind benachbart. Dies bedeutet, dass die chromatische Zahl dieses Graphen gleich 4 ist (siehe Knotenfärbung). Außerdem können die Kanten mit 3 Farben so gefärbt werden, dass benachbarte Kanten immer unterschiedlich gefärbt sind (siehe Abbildungen). Mit 2 Farben ist das nicht möglich, sodass der chromatische Index für die Kantenfärbung gleich 3 ist (das nebenstehende Bild veranschaulicht diese Färbungen).

Der Tetraedergraph ist selbstdual.

Um die entsprechende nötige Anzahl der Farben für die Flächen oder Gebiete zu bestimmen, ist der duale Graph hilfreich, der in diesem Fall selbst ein Tetraedergraph mit 4 Knoten, 6 Kanten und 4 Gebieten ist. Die Knoten dieses Graphen werden dabei den Gebieten des ursprünglichen Tetraedergraph eineindeutig (bijektiv) zugeordnet und umgekehrt (siehe bijektive Funktion und Abbildung oben). Die Knoten des dualen Tetraedergraphen können wie gesagt offensichtlich nur mit 4 Farben so gefärbt werden, dass benachbarte Knoten immer unterschiedlich gefärbt sind. Daraus lässt sich indirekt schließen: Weil die chromatische Zahl gleich 4 ist, sind 4 Farben für eine solche Flächenfärbung des Tetraeders oder eine Färbung der Gebiete des Tetraeders nötig.

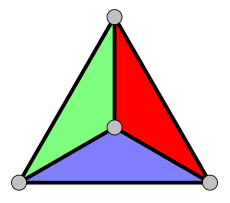
Die 3 aufgeschnittenen Kanten jedes Netzes (siehe oben) bilden zusammen mit den Ecken (Knoten) einen Spannbaum des Tetraedergraphen. Jedes Netz entspricht genau einem Spannbaum und umgekehrt, sodass hier eine eineindeutige (bijektive) Zuordnung zwischen Netzen und Spannbäumen besteht. Wenn man ein Tetraedernetz ohne das äußere Gebiet als Graphen betrachtet, erhält man als dualen Graphen jeweils einem Baum mit 4 Knoten und 3 Kanten und dem maximalen Knotengrad 3. Jede Fläche des Tetraeders wird dabei einem Knoten des Baums zugeordnet. Dabei kommen die 2 graphentheoretischen Konstellationen (siehe Isomorphie von Graphen) jeweils einmal vor.

Der Tetraedergraph besitzt 6 Hamiltonkreise, aber keine Eulerkreise.^[9]

Raumfüllungen mit regelmäßigen Tetraedern[Bearbeiten | Quelltext bearbeiten]

Der dreidimensionale euklidische Raum kann lückenlos mit platonischen Körpern oder archimedischen Körpern gleicher Kantenlänge ausgefüllt werden. Solche dreidimensionalen Parkettierungen werden Raumfüllung genannt. Die folgenden Raumfüllungen enthalten Tetraeder:

Anwendungen[Bearbeiten | Quelltext bearbeiten]

Obwohl das Tetraeder nicht Stein einer Parkettierung des Raumes ist, tritt es im kubischen Kristallsystem auf (siehe oben).

In der Chemie spielt das Tetraeder bei der räumlichen Anordnung von Atomen in Verbindungen eine große Rolle. Einfache Molekülgestalten lassen sich mit dem VSEPR-Modell vorhersagen. So sind die vier Wasserstoffatome im Methanmolekül tetraedrisch um das Kohlenstoffatom angeordnet, da so der Bindungswinkel am größten wird. Auch die Kohlenstoffatome im Diamantgitter sind tetraedrisch angeordnet, jedes Atom ist von vier weiteren Atomen umgeben. Das Kohlenstoff-Atom befindet sich dann nach dem Orbital-Modell in sp³-Hybridisierung.

Das Tetraeder war auch für den Tetra Pak wegen dessen ursprünglicher Form namensgebend.

Alexander Graham Bell hat mit vielzelligen Kastendrachen (Flugdrachen) experimentiert, deren Einzelzellen die Form eines Tetraeders haben. Diese meist imposanten Drachen werden als „Bell-Tetraeder“ bezeichnet. Meistens werden 4 oder 10 oder 20 Einzelzellen zu einem Verbund zusammengefügt, welcher dann auch wieder die Form eines Tetraeders hat. Es sind aber auch andere Verbundformen möglich.

In vielen Pen-&-Paper-Rollenspielen werden Tetraeder als vierseitige Spielwürfel (W4) verwendet.

Weitere technische Anwendungen lehnen sich an die Struktur an, die sich durch die vom Tetraederzentrum in die vier Raumecken weisenden Strecken ergibt:

• Tetrapoden, die an Küsten als Wellenbrecher eingesetzt werden
• sog. Krähenfüße, eine Defensivwaffe, die von Polizei und Militär gegen Autos eingesetzt wird, um deren Reifen platzen zu lassen.

Ein Tetraeder im allgemeinen Sinn, also ein Körper mit vier Seitenflächen, ist immer eine dreiseitige Pyramide, also mit einem Dreieck als Grundfläche und drei Dreiecken als Seitenflächen, und hat daher auch vier Ecken sowie sechs Kanten. Da er die für einen Körper im Raum kleinste mögliche Zahl von Ecken und Seiten hat, wird er in der Fachsprache dreidimensionales Simplex oder 3-Simplex genannt. Die zweidimensionalen Simplizes sind die Dreiecke.

• Jedes 3-Simplex besitzt eine Umkugel und eine Inkugel.
• Der Schwerpunkt ist der Schnittpunkt der Verbindungsstrecken zwischen den Ecken und den Schwerpunkten der gegenüberliegenden Dreiecke und teilt diese im Verhältnis 3:1 (Satz von Commandino).
• Jedes 3-Simplex ist die konvexe Hülle seiner vier Ecken.
• Es ist das einzige bekannte Polyeder neben dem Szilassi-Polyeder, bei dem alle Seiten zueinander benachbart sind.
• Jedes Tetraeder kann in zwei (volumen)gleiche ähnliche Tetraeder sowie zwei (volumen)gleiche unähnliche Prismen zerteilt werden (Elemente XII, 3).

Im

${displaystyle mathbb {R} ^{3}}$

kann ein Tetraeder auch durch einen Punkt und den drei Vektoren zu den angrenzenden Punkten beschrieben werden. Bezeichnet man diese Vektoren mit

${displaystyle {vec {a}},{vec {b}},{vec {c}}}$

, so berechnet sich das Volumen des Tetraeders mit

${displaystyle textstyle V={frac {1}{6}}cdot left|det left[{begin{smallmatrix}{vec {a}}\{vec {b}}\{vec {c}}end{smallmatrix}}right]right|={frac {1}{6}}cdot left|({vec {a}}times {vec {b}})cdot {vec {c}}right|}$

, also

${displaystyle {frac {1}{6}}}$

des Betrags des Spatproduktes.

Die Summe der einheitlich nach außen oder innen weisenden Normaleneinheitsvektoren, die mit dem Inhalt der Fläche multipliziert werden, auf der sie stehen, ist der Nullvektor, denn

${displaystyle {vec {a}}times {vec {b}}+{vec {b}}times {vec {c}}+{vec {c}}times {vec {a}}+({vec {c}}-{vec {a}})times ({vec {b}}-{vec {a}})={vec {0}}}$

Berechnung eines beliebigen Tetraeders[Bearbeiten | Quelltext bearbeiten]

Ein Tetraeder besitzt 6 Kanten. Ein Dreieck ist durch die Angabe dreier Seitenlängen bestimmt. Jede weitere Kante kann in gewissen Grenzen frei gewählt werden. Liegen also 6 voneinander unabhängige Angaben zur Größe von Kanten oder Winkeln vor, kann man daraus die jeweils fehlenden übrigen Kanten oder Winkel berechnen.

Volumen[Bearbeiten | Quelltext bearbeiten]

Die Volumenformel des allgemeinen Tetraeders wurde von Leonhard Euler angegeben.^[10][11] Mit dieser Formel kann das Volumen des allgemeinen Tetraeders mit Hilfe der 6 Kantenlängen des Tetraeders berechnet werden.^[12] Der Volumenformel des allgemeinen Tetraeders liegt also die gleiche Aufgabenstellung für Tetraeder zugrunde wie für Dreiecke der Formel von Heron.

Sind

${displaystyle a,b,c}$

die Kantenlängen der dreieckigen Grundfläche des Tetraeders und

${displaystyle a’,b’,c’}$

die Längen der im Raum gegenüberliegenden Kanten, dann gilt für das Volumen

${displaystyle V}$

des Tetraeders:

${displaystyle V={tfrac {1}{12}}cdot {sqrt {a^{2}cdot a’^{2}cdot f_{a}+b^{2}cdot b’^{2}cdot f_{b}+c^{2}cdot c’^{2}cdot f_{c}-delta }}}$

mit

${displaystyle f_{a}=b^{2}+b’^{2}+c^{2}+c’^{2}-a^{2}-a’^{2}}$

${displaystyle f_{b}=a^{2}+a’^{2}+c^{2}+c’^{2}-b^{2}-b’^{2}}$

${displaystyle f_{c}=a^{2}+a’^{2}+b^{2}+b’^{2}-c^{2}-c’^{2}}$

${displaystyle delta =a^{2}cdot b^{2}cdot c^{2}+a^{2}cdot b’^{2}cdot c’^{2}+a’^{2}cdot b^{2}cdot c’^{2}+a’^{2}cdot b’^{2}cdot c^{2}}$

Zur Berechnung des Volumens können auch die folgenden Gleichungen verwendet werden, die auf Determinanten symmetrischer Matrizen beruhen:^[13][14][15]

${displaystyle {begin{aligned}288cdot V^{2}&=det {begin{pmatrix}0&c^{2}&b^{2}&a’^{2}&1\c^{2}&0&a^{2}&b’^{2}&1\b^{2}&a^{2}&0&c’^{2}&1\a’^{2}&b’^{2}&c’^{2}&0&1\1&1&1&1&0\end{pmatrix}}\&=det {begin{pmatrix}2cdot c^{2}&c^{2}+b^{2}-a^{2}&c^{2}+a’^{2}-b’^{2}\c^{2}+b^{2}-a^{2}&2cdot b^{2}&b^{2}+a’^{2}-c’^{2}\c^{2}+a’^{2}-b’^{2}&b^{2}+a’^{2}-c’^{2}&2cdot a’^{2}\end{pmatrix}}\end{aligned}}}$

Die erste Determinante wird Cayley–Menger-Determinante genannt und dient dazu, den Flächeninhalt von beliebigen Dreiecken (siehe Satz des Heron), das Volumen von beliebigen Tetraedern und allgemein das Volumen eines beliebigen Simplex im

${displaystyle n}$

-dimensionalen Raum zu berechnen.

Oberflächeninhalt[Bearbeiten | Quelltext bearbeiten]

Der Flächeninhalt eines Dreiecks mit gegebenen Seitenlängen kann einzeln berechnet werden. Die Summe der Flächeninhalte der 4 Dreiecke ergibt den Oberflächeninhalt des Tetraeders. Für den Flächeninhalt der dreieckigen Grundfläche mit den Seitenlängen

${displaystyle a,b,c}$

zum Beispiel gilt nach dem Satz des Heron:

${displaystyle A={frac {1}{4}}cdot {sqrt {(a+b+c)cdot (-a+b+c)cdot (a-b+c)cdot (a+b-c)}}}$

Höhen[Bearbeiten | Quelltext bearbeiten]

Weil jedes Tetraeder eine Pyramide ist, gilt für das Volumen

${displaystyle V}$

, den Flächeninhalt

${displaystyle A}$

der Grundfläche und die entsprechende Höhe

${displaystyle h}$

folgende Gleichung:

${displaystyle V={frac {Acdot h}{3}}}$

${displaystyle h={frac {3cdot V}{A}}}$

Das Volumen

${displaystyle V}$

und der Flächeninhalt

${displaystyle A}$

können mit den oben genannten Formeln berechnet und dann eingesetzt werden, um die Höhe zu bestimmen. Die anderen drei Höhen können entsprechend mit Hilfe der Fläche des zur Höhe orthogonalen Dreiecks berechnet werden.

Innenwinkel der Dreiecke[Bearbeiten | Quelltext bearbeiten]

Die Innenwinkel der Dreiecke bestimmt man mit dem Kosinussatz. Für den Innenwinkel

${displaystyle alpha }$

der Grundfläche, der der Seite

${displaystyle a}$

gegenüberliegt, gilt zum Beispiel

${displaystyle alpha =arccos left({frac {b^{2}+c^{2}-a^{2}}{2cdot bcdot c}}right)}$

Winkel zwischen benachbarten Flächen[Bearbeiten | Quelltext bearbeiten]

Der Flächenwinkel an der Kante

${displaystyle a}$

beträgt

${displaystyle beta =arcsin left({frac {3cdot acdot V}{2cdot A_{1}cdot A_{2}}}right)}$

Dabei ist

${displaystyle V}$

das Volumen des Tetraeders und

${displaystyle A_{1}}$

und

${displaystyle A_{2}}$

die Flächeninhalte der zur Kante benachbarten Dreiecke.

Sind die Innenwinkel

${displaystyle alpha _{i,j}}$

,

${displaystyle alpha _{i,k}}$

,

${displaystyle alpha _{i,l}}$

an einer Ecke des Tetraeders gegeben und

${displaystyle beta _{i,j}}$

,

${displaystyle beta _{i,k}}$

,

${displaystyle beta _{i,l}}$

die Flächenwinkel zwischen benachbarten Flächen an dieser Ecke, dann gilt nach dem Kosinussatz für Kugeldreiecke die Gleichung

${displaystyle cos(alpha _{i,j})=cos(alpha _{i,k})cdot cos(alpha _{i,l})+sin(alpha _{i,k})cdot sin(alpha _{i,l})cdot cos(beta _{i,j})}$

Daraus folgt

${displaystyle beta _{i,j}=arccos left({frac {cos(alpha _{i,j})-cos(alpha _{i,k})cdot cos(alpha _{i,l})}{sin(alpha _{i,k})cdot sin(alpha _{i,l})}}right)}$

Ebenso erhält man die Flächenwinkel

${displaystyle beta _{i,k}}$

und

${displaystyle beta _{i,l}}$

.^[16][17]

Raumwinkel in den Ecken[Bearbeiten | Quelltext bearbeiten]

Für die Berechnung der Raumwinkel in den Ecken des Tetraeders werden die Innenwinkel

${displaystyle theta _{a},theta _{b},theta _{c}}$

der drei benachbarten Dreiecke verwendet:

${displaystyle Omega =4cdot arctan left({sqrt {tan left({frac {theta _{s}}{2}}right)cdot tan left({frac {theta _{s}-theta _{a}}{2}}right)cdot tan left({frac {theta _{s}-theta _{b}}{2}}right)cdot tan left({frac {theta _{s}-theta _{c}}{2}}right)}}right)}$

mit

${displaystyle theta _{s}={frac {theta _{a}+theta _{b}+theta _{c}}{2}}}$

Berechnung aus den Koordinaten[Bearbeiten | Quelltext bearbeiten]

Sind die Koordinaten

${displaystyle (x_{1},y_{1},z_{1})}$

,

${displaystyle (x_{2},y_{2},z_{2})}$

,

${displaystyle (x_{3},y_{3},z_{3})}$

,

${displaystyle (x_{4},y_{4},z_{4})}$

der Ecken des Tetraeders bekannt, dann sind die Seitenlängen die euklidischen Abstände

${displaystyle s_{i,j}={sqrt {(x_{i}-x_{j})^{2}+(y_{i}-y_{j})^{2}+(z_{i}-z_{j})^{2}}}}$

der Ecken für alle

${displaystyle i,jin {1,2,3,4}}$

mit

${displaystyle ineq j}$

.

Sind

${displaystyle {vec {a}}={begin{pmatrix}x_{j}-x_{i}\y_{j}-y_{i}\z_{j}-z_{i}end{pmatrix}}}$

und

${displaystyle {vec {b}}={begin{pmatrix}x_{k}-x_{i}\y_{k}-y_{i}\z_{k}-z_{i}end{pmatrix}}}$

zwei Richtungsvektoren, die von derselben Ecke des Tetraeders ausgehen, dann ergibt sich für den Innenwinkel

${displaystyle alpha }$

an dieser Ecke

${displaystyle alpha =arccos left({frac {{vec {a}}cdot {vec {b}}}{|{vec {a}}|cdot |{vec {b}}|}}right)}$

wobei

${displaystyle {vec {a}}cdot {vec {b}}}$

das Skalarprodukt und

${displaystyle |{vec {a}}|}$

und

${displaystyle |{vec {b}}|}$

die Längen der Vektoren

${displaystyle {vec {a}}}$

und

${displaystyle {vec {b}}}$

sind.

Das Volumen kann mithilfe der Determinante

${displaystyle V={frac {1}{6}}cdot det {begin{pmatrix}x_{1}&y_{1}&z_{1}&1\x_{2}&y_{2}&z_{2}&1\x_{3}&y_{3}&z_{3}&1\x_{4}&y_{4}&z_{4}&1\end{pmatrix}}}$

berechnet werden.^[18]

Das regelmäßige Tetraeder kann mithilfe des Kantenkugelradius

${displaystyle r_{k}={tfrac {a}{4}}cdot {sqrt {2}}}$

als Menge von Punkten im dreidimensionalen euklidischen Raum definiert werden. Formal lässt sich diese Menge aufschreiben als

${displaystyle left{(x_{1},x_{2},x_{3})in mathbb {R} ^{3}mid x_{1}+x_{2}+x_{3}leq r_{k} land x_{1}-x_{2}-x_{3}leq r_{k} land -x_{1}+x_{2}-x_{3}leq r_{k} land -x_{1}-x_{2}+x_{3}leq r_{k}right}}$

Für das Innere des Tetraeders muss in den 4 Ungleichungen jeweils

${displaystyle leq }$

durch

${displaystyle <}$

ersetzt werden und für die Oberfläche muss in 1, 2 oder 3 Ungleichungen

${displaystyle leq }$

durch

${displaystyle =}$

ersetzt werden, sodass ein System aus Gleichungen und Ungleichungen entsteht. Bei 1 Gleichung definiert die Menge eine Seitenfläche, also ein gleichseitiges Dreieck, bei 2 Gleichungen eine Kante und bei 3 Gleichungen eine Ecke des Tetraeders.

Nach dieser Definition ist der Mittelpunkt des regelmäßigen Tetraeders der Koordinatenursprung und seine 4 Ecken sind 4 alternierende Ecken eines umbeschriebenen Würfels mit der Seitenlänge

${displaystyle 2cdot r_{k}}$

, dessen Kanten und Seitenflächen parallel zu den 3 Achsen des kartesischen Koordinatensystems verlaufen.

Allgemeiner kann ein regelmäßiges Tetraeder, das eine beliebige Lage im dreidimensionalen euklidischen Raum hat, mithilfe von Vektoren definiert werden. Ist

${displaystyle {vec {m}}}$

der Ortsvektor des Mittelpunkts und sind

${displaystyle {vec {u}}}$

,

${displaystyle {vec {v}}}$

,

${displaystyle {vec {w}}}$

orthogonale Richtungsvektoren, die den Mittelpunkt des Tetraeders mit 3 Mittelpunkten von 3 Kanten verbinden, also ein Orthogonalsystem des dreidimensionalen Vektorraums

${displaystyle mathbb {R} ^{3}}$

bilden, dann lässt sich die Menge der Punkte des Tetraeders definieren als die Menge der Vektoren^[19]

${displaystyle left{{vec {m}}+t_{1}cdot {vec {u}}+t_{2}cdot {vec {v}}+t_{3}cdot {vec {w}}in mathbb {R} ^{3}mid t_{1}+t_{2}+t_{3}leq r_{k} land t_{1}-t_{2}-t_{3}leq r_{k} land -t_{1}+t_{2}-t_{3}leq r_{k} land -t_{1}-t_{2}+t_{3}leq r_{k}right}}$

Die Verallgemeinerungen des Tetraeders in beliebiger Dimension

${displaystyle n}$

werden als

${displaystyle n}$

-dimensionale Simplexe bezeichnet. Das

${displaystyle n}$

-dimensionale Simplex hat

${displaystyle n+1}$

Ecken und wird von

${displaystyle n+1}$

Simplexen der Dimension

${displaystyle n-1}$

(als Facetten) begrenzt. Das nulldimensionales Simplex ist ein Punkt, das eindimensionales Simplex ist eine Strecke, das zweidimensionales Simplex ist ein Dreieck, das dreidimensionale Simplex ist ein Tetraeder. Das vierdimensionale Äquivalent zum Tetraeder, das Pentachoron, hat 5 Ecken, 10 Kanten, 10 Dreiecke als Seitenflächen und 5 dreidimensionale Tetraeder als Facetten.

Die Koordinaten eines regulären

${displaystyle n}$

-dimensionalen Simplex können als Menge im

${displaystyle n}$

-dimensionalen euklidischen Raum definiert werden:

${displaystyle left{xin mathbb {R} ^{n} {Bigg |} sum _{i=1}^{n}x_{i}=x_{1}+x_{2}+ldots +x_{n+1}leq 1 land forall i: -(n+1+{sqrt {n+1}})cdot x_{i}+sum _{i=1}^{n}x_{i}leq 1 right}}$

oder auch als Menge im

${displaystyle n+1}$

-dimensionalen euklidischen Raum

${displaystyle left{xin mathbb {R} ^{n+1} {Bigg |} sum _{i=1}^{n+1}x_{i}=x_{1}+x_{2}+ldots +x_{n+1}=1 land forall i: x_{i}geq 0 right}}$

Beispielsweise für

${displaystyle n=2}$

ergibt sich hier ein gleichseitiges Dreieck, das von den Punkten

${displaystyle (1,0,0)}$

,

${displaystyle (0,1,0)}$

,

${displaystyle (0,0,1)}$

im dreidimensionalen Raum aufgespannt wird.^[20]

Das Sierpinski-Tetraeder ist die dreidimensionale Verallgemeinerung des Sierpinski-Dreiecks. Die Startfigur ist ein Tetraeder. Aus dessen Mitte wird in jedem Iterationsschritt ein Oktaeder mit halber Kantenlänge herausgeschnitten. Übrig bleiben 4 Tetraeder, aus denen wieder je ein Oktaeder herausgeschnitten wird usw.^[21][22]

Nach dem Iterationsschritt

${displaystyle k}$

sind offensichtlich

${displaystyle 4^{k}}$

Teil-Tetraeder mit derselben Seitenlänge entstanden. Die Anzahl der herausgeschnittenen Oktaeder mit verschiedener Seitenlänge beträgt

${displaystyle {frac {4^{k}-1}{3}}}$

.

Die Dimension für dieses Gebilde ist

${displaystyle D={frac {log(4)}{log(2)}}=2}$

, obwohl es sich hierbei um eine Figur im dreidimensionalen Raum handelt. Mit einer zunehmenden Zahl von Iterationsschritten geht das Volumen der Figur gegen 0, der Flächeninhalt der Oberfläche bleibt jedoch konstant, weil sich die Anzahl der Seitenflächen der zueinander deckungsgleichen Teil-Tetraeder mit jedem Iterationsschritt vervierfacht, während sich die Seitenlänge dieser Seitenflächen, die alle deckungsgleiche Dreiecke sind, halbiert.

1. ↑ Kurt Peter Müller: Raumgeometrie: Raumphänomene – Konstruieren – Berechnen. 2., überarbeitete und erweiterte Auflage. Vieweg+Teubner, 2004, ISBN 978-3-519-12397-2, S. 81.
2. ↑ Jürgen Köller: Tetraeder. Vom Tetraeder zu anderen Körpern. mathematische-basteleien, abgerufen am 5. September 2020. 
3. ↑ Eric Weisstein, Frank Jackson: Regular Tetrahedron. Umkugelradius, Formel (5). In: MathWorld Wolfram. A Wolfram Web Resource, abgerufen am 19. Juni 2020. 
4. ↑ Eric Weisstein, Frank Jackson: Regular Tetrahedron. Kantenkugelradius, Formel (10). In: MathWorld Wolfram. A Wolfram Web Resource, abgerufen am 19. Juni 2020. 
5. ↑ Eric Weisstein, Frank Jackson: Regular Tetrahedron. Inkugelradius, Formel (4). In: MathWorld Wolfram. A Wolfram Web Resource, abgerufen am 19. Juni 2020. 
6. ↑ Harish Chandra Rajpoot: Solid angles subtended by the platonic solids (regular polyhedra) at their vertices. SlideShare, März 2015, abgerufen am 16. Juni 2020. 
7. ↑ Alternativer Ausdruck für
   ${displaystyle cos Omega }$

   . WolramAlpha, abgerufen am 16. Juni 2020. 

8. ↑ Eric Weisstein, Frank Jackson: Regular Tetrahedron. 2 Netze, oberhalb Formel (1). In: Wolfram MathWorld. Wolfram Research, Inc., abgerufen am 19. Juni 2020. 
9. ↑ Wolfram MathWorld: Tetrahedral Graph
10. ↑ Maximilian Miller: Stereometrie. 1957, S. 41
11. ↑ Der Titel der Abhandlung E 231 lautet auf Deutsch etwa wie folgt: Darlegung einiger kennzeichnender Eigenschaften, mit denen von ebenen Flächen eingeschlossene Körper ausgestattet sind. In dieser Abhandlung gibt Euler den ersten Beweis der Polyederformel an, welche er schon in einer früheren Abhandlung (E 230, abgedruckt unter Elementa doctrinae solidorum, Novi commentarii academiae scientiarum Petropolitanae 4, S. 109–140; vgl. Einleitung zu den Commentationes geometricae) erwähnt, aber noch nicht bewiesen hatte.
12. ↑ Andreas Speiser et al.: Leonhardi Euleri Opera omnia. Series prima. Opera mathematica. Volumen XXVI: Commentationes geometricae. Volumen I. 1953, S. 106–107
13. ↑ I. N. Bronstein, K. A. Semendjajev et al.: Taschenbuch der Mathematik. 2008, S. 157
14. ↑ György Hajós: Einführung in die Geometrie. 1970, S. 383
15. ↑ Alexander Ostermann, Gerhard Wanner: Geometry by Its History. 2012, S. 297
16. ↑ Stack Exchange: Dihedral angles between tetrahedron faces from triangles’ angles at the tip
17. ↑ G. Richardson: The Trigonometry of the Tetrahedron. In: The Mathematical Gazette. 2, Nr. 32, 1. März 1902, S. 149–158. doi:10.2307/3603090.
18. ↑ Wolfram MathWorld: Tetrahedron
19. ↑ Wolfram MathWorld: Regular Tetrahedron
20. ↑ Martin Henk, Jürgen Richter-Gebert, Günter M. Ziegler, Technische Universität Berlin: Basic properties of convex polytopes
21. ↑ Wolfram MathWorld: Tetrix
22. ↑ Gayla Chandler, Hideki Tsuiki: Photographs: Sierpinski Tetrahedron and its Complement