before-content-x4
アルガナの図は、飛行機の複合数の幾何学的表現の方法です [初め] 。組み合わせた番号
 ポイントはそれに対応します
ポイントはそれに対応します
 平面上のデカルト座標系で。座標系の始まりは、ゼロの数と、カットオフの軸 – 実数の収集に対応します。
平面上のデカルト座標系で。座標系の始まりは、ゼロの数と、カットオフの軸 – 実数の収集に対応します。
アルガナの図は、1797年にデンマークのカスパーウェッセルの数学によって最初に使用されましたが、彼の作品は1897年にデンマーク科学アカデミーがフランス語翻訳を発行した100年後にのみ発見されました。 [2] 。 1807年、スイスのロバート・アーガンドは仕事を公開しました 幾何学的構造の大きさを提示する特定の方法を作ろうとする試み [3] 、彼は数字とそれらの両方のアクションを解釈しました(追加と乗算)。匿名で出版されたArgandの本は、Joseph Blaise Gergonneによる彼女の出版後に知られるようになりました 純粋で応用された数学の年代記 [4] 。壮大な量の解釈について活発な議論がありました [5] 。図を正しい方法で使用した最初の数学者は、1799年からの論文のカール・フリードリッヒ・ガウスでした。
ウェッセルは、飛行機の指示セクション(ベクター)の平等に関する質問や、法案の個々の権利のみを追加および増殖させるなどの微妙さを扱っていませんでした。座標系の開始をポイントと接続するベクトル
 それは意味しました
それは意味しました
 そして、次の結果を見つけました [6] :
そして、次の結果を見つけました [6] :

基本ユニットはウェッセラです
これに基づいて、彼はそれを結論付けました
 次に、指示されたセクションに、彼は三角形の形で合計数を割り当てました
次に、指示されたセクションに、彼は三角形の形で合計数を割り当てました
 このような特定の数字で、彼はすべてのアクションを検討し、de moivreの式(分数指数についても)を証明し、球形の三角形に関する多くのタスクを解決しました。
このような特定の数字で、彼はすべてのアクションを検討し、de moivreの式(分数指数についても)を証明し、球形の三角形に関する多くのタスクを解決しました。
アルガンダ図 – 正式なアプローチ [ 編集 | コードを編集します ]
乗算を決定するだけです。
なぜなら
-

それで
-

-

つまり、複雑な数です
 実際の数字で識別できます
実際の数字で識別できます
-

したがって
 私
私

それから
-
![{displaystyle {begin{aligned}&(a,b)cdot (x,y)\[2px]={}&(a+b(0,1))cdot (x+y(0,1))\[2px]={}&ax+ay(0,1)+bx(0,1)+by(0,1)^{2}\[2px]={}&ax-by+(ay+bx)cdot (0,1)\[2px]={}&(ax-by,ay+bx).end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99db07e3f41a839f27cd3c104f5113294ae70a70)
H.S.M.コクセター [7] [ 編集 | コードを編集します ]
平面上のポイントは、システムの先頭から出てくる対応するベクター(つまりゼロ)と同じように追加されます。
-

言い換えれば、追加する
 ポイント変換点を使用します
ポイント変換点を使用します
 ポイントへ
ポイントへ

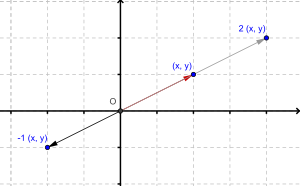
整数による複合数の乗算
ポイントの実数の乗算は、1つの側面です。例えば:
-

-

-

-

乗算
 ポイントの周りの半分の時間です
ポイントの周りの半分の時間です
 したがって、正方形の要素を掛けます
したがって、正方形の要素を掛けます
 それは、正方形(つまり、あなた自身との変換の提出)がポイントの半分の時間であるそのような変換です
それは、正方形(つまり、あなた自身との変換の提出)がポイントの半分の時間であるそのような変換です
 つまり、ポイントの周りの短い時間の4分の1
つまり、ポイントの周りの短い時間の4分の1
 (すなわち、直角の回転) [8] 。
(すなわち、直角の回転) [8] 。
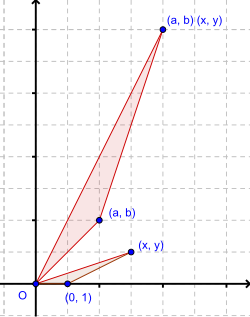
複雑な数値を掛ける。デカルト座標

複雑な数値を掛ける。極座標
したがって、任意の任意の数字による乗算は、ポイントの変換でなければなりません
 永続的なポイントであり、中央の均一性の両方を含む
永続的なポイントであり、中央の均一性の両方を含む
 周りの革命も同様です
周りの革命も同様です
 特別なケースとして。任意のポイントを掛けます
特別なケースとして。任意のポイントを掛けます
 固定点で
固定点で
 中央のスパイラルの類似性として定義されます
中央のスパイラルの類似性として定義されます
 ポイントを実施します
ポイントを実施します
 ポイントへ
ポイントへ
 [9] 。ポイントの場合
[9] 。ポイントの場合
 私
私
 それぞれ極座標があります
それぞれ極座標があります
 私
私
 あれは
あれは
-

次に、スパイラルの類似性が増加します
 に
に
 追加します
追加します
 する
する
 座標を変換します
座標を変換します
-

座標用
-

-

したがって、パターン
-

- ↑ アルガンダ図 、 [の:] PWN百科事典 [オンライン] [アクセス2022-12-03] 。
- ↑ Caspar Wessel: 管理の分析的表現に関するエッセイ、アプリケーションなど 。 1897。
- ↑ ジャン・ロバート・ホールド: 幾何学的構造の架空の量を表す方法に関するエッセイ 。パリ:1806。
- ↑ 「純粋で応用された数学の年代記」。 4、1813/14。ジョセフ・ブレイズ・ゲルゴンヌ。
- ↑ 19世紀の最古から初めから数学の歴史(ロシア語から翻訳) 。 A.P. Juszkiewicz(編)。 T. 3.ワルシャワ:PWN、1977、p。71。
- ↑ 19世紀の最古から初めから数学の歴史(ロシア語から翻訳) 。 A.P. Juszkiewicz(編)。 T. 3.ワルシャワ:PWN、1977、pp。70–71。
- ↑ Coxeter H.S.M。: 古代および新しい幾何学の紹介(英語から翻訳) 。ワルシャワ:PWN、1967、pp。156–158。
- ↑ ハーディG.H。: 純粋な数学 。 WYD。 10.ロンドン:1955年、s。 83。
- ↑ クラインF。: 最初のボリュームからの高い観点からの元素数学。算術、代数、分析 。 WYD。 3.ベルリン:1928年、s。 57。
- Coxeter H.S.M。: 古代および新しい幾何学の紹介(英語から翻訳) 。ワルシャワ:PWN、1967。
- クラインF。: 最初のボリュームからの高い観点からの元素数学。算術、代数、分析 。 WYD。 3.ベルリン:1928年。
- ハーディG.H。: 純粋な数学 。 WYD。 10.ロンドン:1955年。
- 19世紀の最古から初めから数学の歴史(ロシア語から翻訳) 。 A.P. Juszkiewicz(編)。 T. 3.ワルシャワ:PWN、1977。
- Birkhoff G.、Mac Lane S。: 現代の代数レビュー(英語から翻訳) 。編3.ワルシャワ:PWN、1966。
after-content-x4





 ポイントはそれに対応します
ポイントはそれに対応します  平面上のデカルト座標系で。座標系の始まりは、ゼロの数と、カットオフの軸 – 実数の収集に対応します。
平面上のデカルト座標系で。座標系の始まりは、ゼロの数と、カットオフの軸 – 実数の収集に対応します。  それは意味しました
それは意味しました  そして、次の結果を見つけました [6] :
そして、次の結果を見つけました [6] :  次に、指示されたセクションに、彼は三角形の形で合計数を割り当てました
次に、指示されたセクションに、彼は三角形の形で合計数を割り当てました  このような特定の数字で、彼はすべてのアクションを検討し、de moivreの式(分数指数についても)を証明し、球形の三角形に関する多くのタスクを解決しました。
このような特定の数字で、彼はすべてのアクションを検討し、de moivreの式(分数指数についても)を証明し、球形の三角形に関する多くのタスクを解決しました。 


 実際の数字で識別できます
実際の数字で識別できます 
 私
私 
![{displaystyle {begin{aligned}&(a,b)cdot (x,y)\[2px]={}&(a+b(0,1))cdot (x+y(0,1))\[2px]={}&ax+ay(0,1)+bx(0,1)+by(0,1)^{2}\[2px]={}&ax-by+(ay+bx)cdot (0,1)\[2px]={}&(ax-by,ay+bx).end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99db07e3f41a839f27cd3c104f5113294ae70a70)

 ポイント変換点を使用します
ポイント変換点を使用します  ポイントへ
ポイントへ 




 ポイントの周りの半分の時間です
ポイントの周りの半分の時間です  したがって、正方形の要素を掛けます
したがって、正方形の要素を掛けます  つまり、ポイントの周りの短い時間の4分の1
つまり、ポイントの周りの短い時間の4分の1  (すなわち、直角の回転) [8] 。
(すなわち、直角の回転) [8] 。  中央のスパイラルの類似性として定義されます
中央のスパイラルの類似性として定義されます  ポイントへ
ポイントへ  私
私  あれは
あれは 
 に
に  追加します
追加します  する
する  座標を変換します
座標を変換します 



Recent Comments