before-content-x4
|
|
2013-01のこの記事では、提供された情報の検証が必要です。
信頼できる情報源は、好ましくは書誌的な脚注の形で与えられるべきです。
記事の一部またはすべての情報でさえ、真実ではない場合があります。ソースを欠いているように、それらは挑戦して削除される可能性があります。
この記事の議論には、何を修正すべきかについてのより詳細な情報があります。
欠陥を排除した後、この記事からテンプレート{{refine}}を削除します。
|
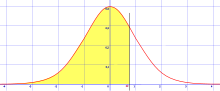
Gaussの分布とも呼ばれる正規分布
確率密度関数 ( ランダム変数の密度 ) – 適切な制限内で計算されたこの関数の積分がランダムイベントの可能性に等しくなるように、確率のサブセクションのために決定される非陰性関数。密度関数は、1次元および多次元確率分布に対して定義されます。密度の分布が呼び出されます 継続的なスケジュール 。
させて
 空間内の確率の分布になります
空間内の確率の分布になります
 (特に単純なリアルで
(特に単純なリアルで
 )。
)。
確率分布の密度
 非陰性のボレロウ関数と呼ばれます
非陰性のボレロウ関数と呼ばれます
 そのように、各ボレロウコレクションについて
そのように、各ボレロウコレクションについて
 平等があります:
平等があります:
-

すなわち、関数からの積分
 コレクションで計算されます
コレクションで計算されます
 確率に等しくなります
確率に等しくなります
 コレクションに割り当てられます
コレクションに割り当てられます

特別な場合は、Lebesgueを使用する必要があります。
Tw。 1 (密度の正規化について)if
 減衰の密度です
減衰の密度です
 これは特に、上記の定義のおかげです。
これは特に、上記の定義のおかげです。
-

すなわち、空間全体で計算された密度関数からの積分
 1に等しい。
1に等しい。
Tw。 2 (特定の密度の分布の存在について)
非陰性のボレロウ関数
 上記の状態を満たすことは、ある確率分布の密度です
上記の状態を満たすことは、ある確率分布の密度です

密度と分布-1次元の場合 [ 編集 | コードを編集します ]
Tw。 3 (分布の計算について)
それを仮定しましょう
 減衰の密度です
減衰の密度です
 次に、分布
次に、分布
 分解
分解
 密度から決定できます
密度から決定できます
-
![{displaystyle F_{P}(x)equiv P(,,(-infty ,x],,)=int limits _{-infty }^{x}f(t)dt.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b3911e704c46f03bf0150bdcb6eaeb506eb0899)
したがって、密度がある場合は、減衰の分布を簡単に表現できます。これは、分布を基本的に(例:正規分布の場合)表現できない場合に役立ちます。
Tw。 4。 特定の分布のために密度の存在に必要かつ十分な条件
 彼の分布には絶対的な連続性があります。
彼の分布には絶対的な連続性があります。
連続性自体は十分な条件ではありません – 密度のない連続分布(例:Cantorの分布)があります。
Tw。 5。 もしも
 分布です。どこでもほぼ異なり、
分布です。どこでもほぼ異なり、
 (ほぼすべての場所で決定されます)どこでもゼロとはほぼ異なり、密度です。
(ほぼすべての場所で決定されます)どこでもゼロとはほぼ異なり、密度です。
密度と期待値1次元の場合 [ 編集 | コードを編集します ]
Tw。 6。 もしも
 密度の連続分布を持つ1次元ランダム変数です
密度の連続分布を持つ1次元ランダム変数です
 式で表現されるのは彼女の期待値です。
式で表現されるのは彼女の期待値です。
-

ランダム変数の合計の密度 [ 編集 | コードを編集します ]
Tw。 7
a) もしも
 私
私
 それらは独立したランダム変数であり、少なくとも1つは連続分布を持ち、その合計には連続的な分布があります。
それらは独立したランダム変数であり、少なくとも1つは連続分布を持ち、その合計には連続的な分布があります。
b) さらに、両方のランダム変数に連続分布がある場合、その合計の密度は密度の織りです。
密度特性-2次元の場合 [ 編集 | コードを編集します ]
密度関数によって制限されているブロックの体積 [ 編集 | コードを編集します ]
Tw。 8。 2つの変数の密度関数を持つ上から制限されたブロックの体積、および平面付きの底から
 それは常に平等です
それは常に平等です
 すなわち
すなわち
-

等しい関数の値からの積分への貢献
 合計
合計
 したがって、密度関数のゼロ以外の領域への上記の統合を狭めることができます。たとえば、この領域が長方形の場合
したがって、密度関数のゼロ以外の領域への上記の統合を狭めることができます。たとえば、この領域が長方形の場合
![{displaystyle [x_{1},x_{2}]times [y_{1},y_{2}],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca62983c1ddb6388bb0073fe15fd43d31c8ba1d9) に
に
-

飛行機の特定の領域からの値の確率 [ 編集 | コードを編集します ]
特定の領域から結果を受信する可能性を計算するために
 平面、この領域の後、密度関数から作成する必要があります。
平面、この領域の後、密度関数から作成する必要があります。
-

たとえば、長方形に属する値を受信する概要の可能性をカウントする場合
![{displaystyle [x_{1},x_{2}]times [y_{1},y_{2}],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca62983c1ddb6388bb0073fe15fd43d31c8ba1d9) これは、間隔の制限でマークされた密度関数からの積分の値に等しくなります。
これは、間隔の制限でマークされた密度関数からの積分の値に等しくなります。
-

ランダム変数の独立性に関する定理 [ 編集 | コードを編集します ]
ランダム変数
 密度が機能します
密度が機能します
-

-

関数の場合、それらは独立しています
 ランダムベクトルの密度です
ランダムベクトルの密度です
 したがって、方程式は真です:
したがって、方程式は真です:
-

古典的なメカニズムでは、たとえば、システムの個々の部分の相互位置の投与と芽の投与によって、物理システムの状態が記述されています。物理システムは、同じ粒子で構成される場合、同じ相互位置とシュートを持つ場合、同一と見なされます。ここでは、古典的なメカニズムは、ポジションとシュートを原則的に測定できるという仮定に基づいています。ただし、これは、小さな質量を持つ粒子を扱っている場合、真実ではありません。この場合、物理システムの実際の動作のより正確な説明は、量子力学を与えます。
量子力学では、位置とシュートの同時に付着していることが放棄されます。見返りに、物理システムの条件は波動関数によって記述されます。物理システムは、同一の波動関数に起因する場合、同一と見なされます。ただし、同一のシステムで実行される測定可能なサイズ(SO -COLLEDの観測値)の測定は、さまざまな結果につながる可能性があります。たとえば、同じ波動関数に記載されている位置、シュート、粒子エネルギーを測定することにより
 特定のランダム分布で結果を受け取ります。
特定のランダム分布で結果を受け取ります。
 波動関数モジュールの正方形に等しくなります。
波動関数モジュールの正方形に等しくなります。
-

どこ
 複雑なカップリングを意味します。
複雑なカップリングを意味します。
一般に、同一のシステムで行われた各測定の結果は、特定の確率分布を持つ多次元ランダム変数です。
after-content-x4

 空間内の確率の分布になります
空間内の確率の分布になります  (特に単純なリアルで
(特に単純なリアルで  )。
)。  そのように、各ボレロウコレクションについて
そのように、各ボレロウコレクションについて  平等があります:
平等があります: 
 コレクションで計算されます
コレクションで計算されます  確率に等しくなります
確率に等しくなります  コレクションに割り当てられます
コレクションに割り当てられます 
 これは特に、上記の定義のおかげです。
これは特に、上記の定義のおかげです。 
 上記の状態を満たすことは、ある確率分布の密度です
上記の状態を満たすことは、ある確率分布の密度です 
 分解
分解 ![{displaystyle F_{P}(x)equiv P(,,(-infty ,x],,)=int limits _{-infty }^{x}f(t)dt.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b3911e704c46f03bf0150bdcb6eaeb506eb0899)
 分布です。どこでもほぼ異なり、
分布です。どこでもほぼ異なり、  (ほぼすべての場所で決定されます)どこでもゼロとはほぼ異なり、密度です。
(ほぼすべての場所で決定されます)どこでもゼロとはほぼ異なり、密度です。  密度の連続分布を持つ1次元ランダム変数です
密度の連続分布を持つ1次元ランダム変数です  式で表現されるのは彼女の期待値です。
式で表現されるのは彼女の期待値です。 
 それらは独立したランダム変数であり、少なくとも1つは連続分布を持ち、その合計には連続的な分布があります。
それらは独立したランダム変数であり、少なくとも1つは連続分布を持ち、その合計には連続的な分布があります。  それは常に平等です
それは常に平等です  すなわち
すなわち 
 合計
合計  したがって、密度関数のゼロ以外の領域への上記の統合を狭めることができます。たとえば、この領域が長方形の場合
したがって、密度関数のゼロ以外の領域への上記の統合を狭めることができます。たとえば、この領域が長方形の場合 ![{displaystyle [x_{1},x_{2}]times [y_{1},y_{2}],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca62983c1ddb6388bb0073fe15fd43d31c8ba1d9) に
に 
 平面、この領域の後、密度関数から作成する必要があります。
平面、この領域の後、密度関数から作成する必要があります。 

 密度が機能します
密度が機能します 

 ランダムベクトルの密度です
ランダムベクトルの密度です  したがって、方程式は真です:
したがって、方程式は真です: 
 特定のランダム分布で結果を受け取ります。
特定のランダム分布で結果を受け取ります。  波動関数モジュールの正方形に等しくなります。
波動関数モジュールの正方形に等しくなります。 
 複雑なカップリングを意味します。
複雑なカップリングを意味します。
Recent Comments