Delaunay triangulation – Wikipedia

Triangulation method

A Delaunay triangulation in the plane with circumcircles shown

In mathematics and computational geometry, a Delaunay triangulation (also known as a Delone triangulation) for a given set P of discrete points in a general position is a triangulation DT(P) such that no point in P is inside the circumcircle of any triangle in DT(P). Delaunay triangulations maximize the minimum of all the angles of the triangles in the triangulation; they tend to avoid sliver triangles. The triangulation is named after Boris Delaunay for his work on this topic from 1934.^[1]

For a set of points on the same line there is no Delaunay triangulation (the notion of triangulation is degenerate for this case). For four or more points on the same circle (e.g., the vertices of a rectangle) the Delaunay triangulation is not unique: each of the two possible triangulations that split the quadrangle into two triangles satisfies the “Delaunay condition”, i.e., the requirement that the circumcircles of all triangles have empty interiors.

By considering circumscribed spheres, the notion of Delaunay triangulation extends to three and higher dimensions. Generalizations are possible to metrics other than Euclidean distance. However, in these cases a Delaunay triangulation is not guaranteed to exist or be unique.

Relationship with the Voronoi diagram[edit]

The Delaunay triangulation with all the circumcircles and their centers (in red).

Connecting the centers of the circumcircles produces the Voronoi diagram (in red).

The Delaunay triangulation of a discrete point set P in general position corresponds to the dual graph of the Voronoi diagram for P.
The circumcenters of Delaunay triangles are the vertices of the Voronoi diagram.
In the 2D case, the Voronoi vertices are connected via edges, that can be derived from adjacency-relationships of the Delaunay triangles: If two triangles share an edge in the Delaunay triangulation, their circumcenters are to be connected with an edge in the Voronoi tesselation.

Special cases where this relationship does not hold, or is ambiguous, include cases like:

• Three or more collinear points, where the circumcircles are of infinite radii.
• Four or more points on a perfect circle, where the triangulation is ambiguous and all circumcenters are trivially identical.
• Edges of the Voronoi diagram going to infinity are not defined by this relation in case of a finite set P. If the Delaunay triangulation is calculated using the Bowyer–Watson algorithm then the circumcenters of triangles having a common vertex with the “super” triangle should be ignored. Edges going to infinity start from a circumcenter and they are perpendicular to the common edge between the kept and ignored triangle.

d-dimensional Delaunay[edit]

For a set P of points in the (d-dimensional) Euclidean space, a Delaunay triangulation is a triangulation DT(P) such that no point in P is inside the circum-hypersphere of any d-simplex in DT(P). It is known^[1] that there exists a unique Delaunay triangulation for P if P is a set of points in general position; that is, the affine hull of P is d-dimensional and no set of d + 2 points in P lie on the boundary of a ball whose interior does not intersect P.

The problem of finding the Delaunay triangulation of a set of points in d-dimensional Euclidean space can be converted to the problem of finding the convex hull of a set of points in (d + 1)-dimensional space. This may be done by giving each point p an extra coordinate equal to |p|², thus turning it into a hyper-paraboloid (this is termed “lifting”); taking the bottom side of the convex hull (as the top end-cap faces upwards away from the origin, and must be discarded); and mapping back to d-dimensional space by deleting the last coordinate. As the convex hull is unique, so is the triangulation, assuming all facets of the convex hull are simplices. Nonsimplicial facets only occur when d + 2 of the original points lie on the same d-hypersphere, i.e., the points are not in general position.^[2]

Properties[edit]

Each frame of the animation shows a Delaunay triangulation of the four points. Halfway through, the triangulating edge flips showing that the Delaunay triangulation maximizes the minimum angle, not the edge-length of the triangles.

Let n be the number of points and d the number of dimensions.

• The union of all simplices in the triangulation is the convex hull of the points.
• The Delaunay triangulation contains
  ${displaystyle Oleft(n^{lceil d/2rceil }right)}$

  simplices.^[3]

• In the plane (d = 2), if there are b vertices on the convex hull, then any triangulation of the points has at most 2n – 2 – b triangles, plus one exterior face (see Euler characteristic).
• If points are distributed according to a Poisson process in the plane with constant intensity, then each vertex has on average six surrounding triangles. More generally for the same process in d dimensions the average number of neighbors is a constant depending only on d.^[4]
• In the plane, the Delaunay triangulation maximizes the minimum angle. Compared to any other triangulation of the points, the smallest angle in the Delaunay triangulation is at least as large as the smallest angle in any other. However, the Delaunay triangulation does not necessarily minimize the maximum angle.^[5] The Delaunay triangulation also does not necessarily minimize the length of the edges.
• A circle circumscribing any Delaunay triangle does not contain any other input points in its interior.
• If a circle passing through two of the input points doesn’t contain any other input points in its interior, then the segment connecting the two points is an edge of a Delaunay triangulation of the given points.
• Each triangle of the Delaunay triangulation of a set of points in d-dimensional spaces corresponds to a facet of convex hull of the projection of the points onto a (d + 1)-dimensional paraboloid, and vice versa.
• The closest neighbor b to any point p is on an edge bp in the Delaunay triangulation since the nearest neighbor graph is a subgraph of the Delaunay triangulation.
• The Delaunay triangulation is a geometric spanner: In the plane (d = 2), the shortest path between two vertices, along Delaunay edges, is known to be no longer than 1.998 times the Euclidean distance between them.^[6]

Visual Delaunay definition: Flipping[edit]

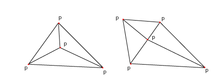
From the above properties an important feature arises: Looking at two triangles △ABD, △BCD with the common edge BD (see figures), if the sum of the angles α + γ ≤ 180°, the triangles meet the Delaunay condition.

This is an important property because it allows the use of a flipping technique. If two triangles do not meet the Delaunay condition, switching the common edge BD for the common edge AC produces two triangles that do meet the Delaunay condition:

• 

  This triangulation does not meet the Delaunay condition (the sum of α and γ is bigger than 180°).

• 

  This pair of triangles does not meet the Delaunay condition (there is a point within the interior of the circumcircle).

• 

  Flipping the common edge produces a valid Delaunay triangulation for the four points.

This operation is called a flip, and can be generalised to three and higher dimensions.^[7]

Algorithms[edit]

We need a robust and fast way to detect if point D lies in the circumcircle of A, B, C

Many algorithms for computing Delaunay triangulations rely on fast operations for detecting when a point is within a triangle’s circumcircle and an efficient data structure for storing triangles and edges. In two dimensions, one way to detect if point D lies in the circumcircle of A, B, C is to evaluate the determinant:^[8]

${displaystyle {begin{aligned}&{begin{vmatrix}A_{x}&A_{y}&A_{x}^{2}+A_{y}^{2}&1\B_{x}&B_{y}&B_{x}^{2}+B_{y}^{2}&1\C_{x}&C_{y}&C_{x}^{2}+C_{y}^{2}&1\D_{x}&D_{y}&D_{x}^{2}+D_{y}^{2}&1end{vmatrix}}\[8pt]={}&{begin{vmatrix}A_{x}-D_{x}&A_{y}-D_{y}&(A_{x}^{2}-D_{x}^{2})+(A_{y}^{2}-D_{y}^{2})\B_{x}-D_{x}&B_{y}-D_{y}&(B_{x}^{2}-D_{x}^{2})+(B_{y}^{2}-D_{y}^{2})\C_{x}-D_{x}&C_{y}-D_{y}&(C_{x}^{2}-D_{x}^{2})+(C_{y}^{2}-D_{y}^{2})end{vmatrix}}>0end{aligned}}}$

A, B, C are sorted in a counterclockwise order, this determinant is positive only if D lies inside the circumcircle.

Flip algorithms[edit]

As mentioned above, if a triangle is non-Delaunay, we can flip one of its edges. This leads to a straightforward algorithm: construct any triangulation of the points, and then flip edges until no triangle is non-Delaunay. Unfortunately, this can take Ω(n²) edge flips.^[9] While this algorithm can be generalised to three and higher dimensions, its convergence is not guaranteed in these cases, as it is conditioned to the connectedness of the underlying flip graph: this graph is connected for two-dimensional sets of points, but may be disconnected in higher dimensions.^[7]

Incremental[edit]

The most straightforward way of efficiently computing the Delaunay triangulation is to repeatedly add one vertex at a time, retriangulating the affected parts of the graph. When a vertex v is added, we split in three the triangle that contains v, then we apply the flip algorithm. Done naïvely, this will take O(n) time: we search through all the triangles to find the one that contains v, then we potentially flip away every triangle. Then the overall runtime is O(n²).

If we insert vertices in random order, it turns out (by a somewhat intricate proof) that each insertion will flip, on average, only O(1) triangles – although sometimes it will flip many more.^[10]
This still leaves the point location time to improve. We can store the history of the splits and flips performed: each triangle stores a pointer to the two or three triangles that replaced it. To find the triangle that contains v, we start at a root triangle, and follow the pointer that points to a triangle that containsv, until we find a triangle that has not yet been replaced. On average, this will also take O(log n) time. Over all vertices, then, this takes O(n log n) time.^[11] While the technique extends to higher dimension (as proved by Edelsbrunner and Shah^[12]), the runtime can be exponential in the dimension even if the final Delaunay triangulation is small.

The Bowyer–Watson algorithm provides another approach for incremental construction. It gives an alternative to edge flipping for computing the Delaunay triangles containing a newly inserted vertex.

Unfortunately the flipping-based algorithms are generally hard to parallelize, since adding some certain point (e.g. the center point of a wagon wheel) can lead to up to O(n) consecutive flips. Blelloch et al.^[13] proposed another version of incremental algorithm based on rip-and-tent, which is practical and highly parallelized with polylogarithmic span.

Divide and conquer[edit]

A divide and conquer algorithm for triangulations in two dimensions was developed by Lee and Schachter and improved by Guibas and Stolfi^[14][15] and later by Dwyer.^[16] In this algorithm, one recursively draws a line to split the vertices into two sets. The Delaunay triangulation is computed for each set, and then the two sets are merged along the splitting line. Using some clever tricks, the merge operation can be done in time O(n), so the total running time is O(n log n).^[17]

For certain types of point sets, such as a uniform random distribution, by intelligently picking the splitting lines the expected time can be reduced to O(n log n) while still maintaining worst-case performance.

A divide and conquer paradigm to performing a triangulation in d dimensions is presented in “DeWall: A fast divide and conquer Delaunay triangulation algorithm in E^d” by P. Cignoni, C. Montani, R. Scopigno.^[18]

The divide and conquer algorithm has been shown to be the fastest DT generation technique sequentially.^[19][20]

Sweephull[edit]

Sweephull^[21] is a hybrid technique for 2D Delaunay triangulation that uses a radially propagating sweep-hull, and a flipping algorithm. The sweep-hull is created sequentially by iterating a radially-sorted set of 2D points, and connecting triangles to the visible part of the convex hull, which gives a non-overlapping triangulation. One can build a convex hull in this manner so long as the order of points guarantees no point would fall within the triangle. But, radially sorting should minimize flipping by being highly Delaunay to start. This is then paired with a final iterative triangle flipping step.

Applications[edit]

The Euclidean minimum spanning tree of a set of points is a subset of the Delaunay triangulation of the same points,^[22] and this can be exploited to compute it efficiently.

For modelling terrain or other objects given a point cloud, the Delaunay triangulation gives a nice set of triangles to use as polygons in the model. In particular, the Delaunay triangulation avoids narrow triangles (as they have large circumcircles compared to their area). See triangulated irregular network.

Delaunay triangulations can be used to determine the density or intensity of points samplings by means of the Delaunay tessellation field estimator (DTFE).

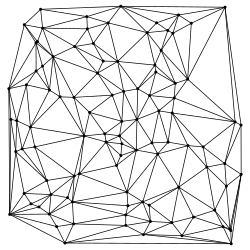A Delaunay triangulation of a random set of 100 points in a plane.

Delaunay triangulations are often used to generate meshes for space-discretised solvers such as the finite element method and the finite volume method of physics simulation, because of the angle guarantee and because fast triangulation algorithms have been developed. Typically, the domain to be meshed is specified as a coarse simplicial complex; for the mesh to be numerically stable, it must be refined, for instance by using Ruppert’s algorithm.

The increasing popularity of finite element method and boundary element method techniques increases the incentive to improve automatic meshing algorithms. However, all of these algorithms can create distorted and even unusable grid elements. Fortunately, several techniques exist which can take an existing mesh and improve its quality. For example, smoothing (also referred to as mesh refinement) is one such method, which repositions nodes to minimize element distortion. The stretched grid method allows the generation of pseudo-regular meshes that meet the Delaunay criteria easily and quickly in a one-step solution.

Constrained Delaunay triangulation has found applications in path planning in automated driving and topographic surveying. ^[23]

See also[edit]

References[edit]

1. ^ ^{a b} Delaunay, Boris (1934). “Sur la sphère vide”. Bulletin de l’Académie des Sciences de l’URSS, Classe des Sciences Mathématiques et Naturelles. 6: 793–800.
2. ^ Fukuda, Komei. “Frequently Asked Questions in Polyhedral Computation”. www.cs.mcgill.ca. Retrieved 29 October 2018.
3. ^ Seidel, Raimund (1995). “The upper bound theorem for polytopes: an easy proof of its asymptotic version”. Computational Geometry. 5 (2): 115–116. doi:10.1016/0925-7721(95)00013-Y.
4. ^ Meijering, J. L. (1953), “Interface area, edge length, and number of vertices in crystal aggregates with random nucleation” (PDF), Philips Research Reports, 8: 270–290, archived from the original (PDF) on 2017-03-08. As cited by Dwyer, Rex A. (1991), “Higher-dimensional Voronoĭ diagrams in linear expected time”, Discrete and Computational Geometry, 6 (4): 343–367, doi:10.1007/BF02574694, MR 1098813.
5. ^ Edelsbrunner, Herbert; Tan, Tiow Seng; Waupotitsch, Roman (1992), “An O(n² log n) time algorithm for the minmax angle triangulation” (PDF), SIAM Journal on Scientific and Statistical Computing, 13 (4): 994–1008, CiteSeerX 10.1.1.66.2895, doi:10.1137/0913058, MR 1166172, archived from the original (PDF) on 2017-02-09, retrieved 2017-10-24.
6. ^ Xia, Ge (2013), “The stretch factor of the Delaunay triangulation is less than 1.998”, SIAM Journal on Computing, 42 (4): 1620–1659, arXiv:1103.4361, doi:10.1137/110832458, MR 3082502, S2CID 6646528
7. ^ ^{a b} De Loera, Jesús A.; Rambau, Jörg; Santos, Francisco (2010). Triangulations, Structures for Algorithms and Applications. Algorithms and Computation in Mathematics. Vol. 25. Springer.
8. ^ Guibas, Leonidas; Stolfi, Jorge (1985). “Primitives for the manipulation of general subdivisions and the computation of Voronoi”. ACM Transactions on Graphics. 4 (2): 74–123. doi:10.1145/282918.282923. S2CID 52852815.
9. ^ Hurtado, F.; Noy, M.; Urrutia, J. (1999). “Flipping Edges in Triangulations”. Discrete & Computational Geometry. 22 (3): 333–346. doi:10.1007/PL00009464.
10. ^ Guibas, Leonidas J.; Knuth, Donald E.; Sharir, Micha (1992). “Randomized incremental construction of Delaunay and Voronoi diagrams”. Algorithmica. 7 (1–6): 381–413. doi:10.1007/BF01758770. S2CID 3770886.
11. ^ de Berg, Mark; Otfried Cheong; Marc van Kreveld; Mark Overmars (2008). Computational Geometry: Algorithms and Applications (PDF). Springer-Verlag. ISBN 978-3-540-77973-5. Archived from the original (PDF) on 2009-10-28. Retrieved 2010-02-23.
12. ^ Edelsbrunner, Herbert; Shah, Nimish (1996). “Incremental Topological Flipping Works for Regular Triangulations”. Algorithmica. 15 (3): 223–241. doi:10.1007/BF01975867. S2CID 12976796.
13. ^ Blelloch, Guy; Gu, Yan; Shun, Julian; and Sun, Yihan. Parallelism in Randomized Incremental Algorithms Archived 2018-04-25 at the Wayback Machine. SPAA 2016. doi:10.1145/2935764.2935766.
14. ^ Guibas, Leonidas; Stolfi, Jorge (April 1985). “Primitives for the manipulation of general subdivisions and the computation of Voronoi”. ACM Transactions on Graphics. 4 (2): 74–123. doi:10.1145/282918.282923. S2CID 52852815.
15. ^ “COMPUTING CONSTRAINED DELAUNAY TRIANGULATIONS IN THE PLANE”. www.geom.uiuc.edu. Archived from the original on 22 September 2017. Retrieved 25 April 2018.
16. ^ Dwyer, Rex A. (November 1987). “A faster divide-and-conquer algorithm for constructing delaunay triangulations”. Algorithmica. 2 (1–4): 137–151. doi:10.1007/BF01840356. S2CID 10828441.
17. ^ Leach, G. (June 1992). “Improving Worst-Case Optimal Delaunay Triangulation Algorithms”. 4th Canadian Conference on Computational Geometry. CiteSeerX 10.1.1.56.2323.
18. ^ Cignoni, P.; C. Montani; R. Scopigno (1998). “DeWall: A fast divide and conquer Delaunay triangulation algorithm in E^d“. Computer-Aided Design. 30 (5): 333–341. doi:10.1016/S0010-4485(97)00082-1.
19. ^ A Comparison of Sequential Delaunay Triangulation Algorithms “Archived copy” (PDF). Archived from the original (PDF) on 2012-03-08. Retrieved 2010-08-18.{{cite web}}: CS1 maint: archived copy as title (link)
20. ^ “Triangulation Algorithms and Data Structures”. www.cs.cmu.edu. Archived from the original on 10 October 2017. Retrieved 25 April 2018.
21. ^ “S-hull” (PDF). s-hull.org. Archived (PDF) from the original on 2013-10-27. Retrieved 25 April 2018.
22. ^ Franz Aurenhammer; Rolf Klein; Der-tsai Lee (26 June 2013). Voronoi Diagrams And Delaunay Triangulations. World Scientific Publishing Company. pp. 197–. ISBN 978-981-4447-65-2.
23. ^ Sterling J Anderson; Sisir B. Karumanchi; Karl Iagnemma (5 July 2012). “Constraint-based planning and control for safe, semi-autonomous operation of vehicles” (PDF). 2012 IEEE Intelligent Vehicles Symposium. IEEE. doi:10.1109/IVS.2012.6232153. Archived from the original (PDF) on 28 February 2019. Retrieved 27 February 2019.

External links[edit]

Software[edit]