Power of a point – Wikipedia

Relative distance of a point from a circle

In elementary plane geometry, the power of a point is a real number that reflects the relative distance of a given point from a given circle. It was introduced by Jakob Steiner in 1826.^[1]

Specifically, the power

${displaystyle Pi (P)}$

of a point

${displaystyle P}$

with respect to a circle

${displaystyle c}$

with center

${displaystyle O}$

and radius

${displaystyle r}$

is defined by

${displaystyle Pi (P)=|PO|^{2}-r^{2}.}$

If

${displaystyle P}$

is outside the circle, then

${displaystyle Pi (P)>0}$

${displaystyle P}$

is on the circle, then

${displaystyle Pi (P)=0}$

and
if

${displaystyle P}$

is inside the circle, then

${displaystyle Pi (P)<0}$

.

Due to the Pythagorean theorem the number

${displaystyle Pi (P)}$

has the simple geometric meanings shown in the diagram: For a point

${displaystyle P}$

outside the circle

${displaystyle Pi (P)}$

is the squared tangential distance

${displaystyle |PT|}$

of point

${displaystyle P}$

to the circle

${displaystyle c}$

.

Points with equal power, isolines of

${displaystyle Pi (P)}$

, are circles concentric to circle

${displaystyle c}$

.

Steiner used the power of a point for proofs of several statements on circles, for example:

• Determination of a circle, that intersects four circles by the same angle.^[2]
• Solving the Problem of Apollonius
• Construction of the Malfatti circles:^[3] For a given triangle determine three circles, which touch each other and two sides of the triangle each.
• Spherical version of Malfatti’s problem:^[4] The triangle is a spherical one.

Essential tools for investigations on circles are the radical axis of two circles and the radical center of three circles.

The power diagram of a set of circles divides the plane into regions within which the circle minimizing the power is constant.

More generally, French mathematician Edmond Laguerre defined the power of a point with respect to any algebraic curve in a similar way.

Geometric properties[edit]

Besides the properties mentioned in the lead there are further properties:

Orthogonal circle[edit]

For any point

${displaystyle P}$

outside of the circle

${displaystyle c}$

there are two tangent points

${displaystyle T_{1},T_{2}}$

on circle

${displaystyle c}$

, which have equal distance to

${displaystyle P}$

. Hence the circle

${displaystyle o}$

with center

${displaystyle P}$

through

${displaystyle T_{1}}$

passes

${displaystyle T_{2}}$

, too, and intersects

${displaystyle c}$

orthogonal:

• The circle with center
  ${displaystyle P}$

  and radius

  ${displaystyle {sqrt {Pi (P)}}}$

  intersects circle

  ${displaystyle c}$

  orthogonal.

If the radius

${displaystyle rho }$

of the circle centered at

${displaystyle P}$

is different from

${displaystyle {sqrt {Pi (P)}}}$

one gets the angle of intersection

${displaystyle varphi }$

between the two circles applying the Law of cosines (see the diagram):

${displaystyle rho ^{2}+r^{2}-2rho rcos varphi =|PO|^{2}}$

${displaystyle rightarrow cos varphi ={frac {rho ^{2}+r^{2}-|PO|^{2}}{2rho r}}={frac {rho ^{2}-Pi (P)}{2rho r}}}$

(

${displaystyle PS_{1}}$

and

${displaystyle OS_{1}}$

are normals to the circle tangents.)

If

${displaystyle P}$

lies inside the blue circle, then

${displaystyle Pi (P)<0}$

and

${displaystyle varphi }$

is always different from

${displaystyle 90^{circ }}$

.

If the angle

${displaystyle varphi }$

is given, then one gets the radius

${displaystyle rho }$

by solving the quadratic equation

${displaystyle rho ^{2}-2rho rcos varphi -Pi (P)=0}$

.

Intersecting secants theorem, intersecting chords theorem[edit]

For the intersecting secants theorem and chord theorem the power of a point plays the role of an invariant:

Radical axis[edit]

Let

${displaystyle P}$

be a point and

${displaystyle c_{1},c_{2}}$

two non concentric circles with
centers

${displaystyle O_{1},O_{2}}$

and radii

${displaystyle r_{1},r_{2}}$

. Point

${displaystyle P}$

has the power

${displaystyle Pi _{i}(P)}$

with respect to circle

${displaystyle c_{i}}$

. The set of all points

${displaystyle P}$

with

${displaystyle Pi _{1}(P)=Pi _{2}(P)}$

is a line called radical axis. It contains possible common points of the circles and is perpendicular to line

${displaystyle {overline {O_{1}O_{2}}}}$

.

Secants theorem, chords theorem: common proof[edit]

Both theorems, including the tangent-secant theorem, can be proven uniformly:

Let

${displaystyle P:{vec {p}}}$

be a point,

${displaystyle c:{vec {x}}^{2}-r^{2}=0}$

a circle with the origin as its center and

${displaystyle {vec {v}}}$

an arbitrary unit vector. The parameters

${displaystyle t_{1},t_{2}}$

of possible common points of line

${displaystyle g:{vec {x}}={vec {p}}+t{vec {v}}}$

(through

${displaystyle P}$

) and circle

${displaystyle c}$

can be determined by inserting the parametric equation into the circle’s equation:

${displaystyle ({vec {p}}+t{vec {v}})^{2}-r^{2}=0quad rightarrow quad t^{2}+2t;{vec {p}}cdot {vec {v}}+{vec {p}}^{2}-r^{2}=0 .}$

From Vieta’s theorem one finds:

${displaystyle t_{1}cdot t_{2}={vec {p}}^{2}-r^{2}=Pi (P)}$

. (independent of

${displaystyle {vec {v}}}$

 !)

${displaystyle Pi (P)}$

is the power of

${displaystyle P}$

with respect for circle

${displaystyle c}$

.

Because of

${displaystyle |{vec {v}}|=1}$

one gets the following statement for the points

${displaystyle S_{1},S_{2}}$

:

${displaystyle |PS_{1}|cdot |PS_{2}|=t_{1}t_{2}=Pi (P) }$

, if

${displaystyle P}$

is outside the circle,

${displaystyle |PS_{1}|cdot |PS_{2}|=-t_{1}t_{2}=-Pi (P) }$

, if

${displaystyle P}$

is inside the circle (

${displaystyle t_{1},t_{2}}$

have different signs !).

In case of

${displaystyle t_{1}=t_{2}}$

line

${displaystyle g}$

is a tangent and

${displaystyle Pi (P)}$

the square of the tangential distance of point

${displaystyle P}$

to circle

${displaystyle c}$

.

Similarity points, common power of two circles[edit]

Similarity points[edit]

Similarity points are an essential tool for Steiner’s investigations on circles.^[5]

Given two circles

${displaystyle c_{1}:({vec {x}}-{vec {m}}_{1})-r_{1}^{2}=0,quad c_{2}:({vec {x}}-{vec {m}}_{2})-r_{2}^{2}=0 .}$

A homothety (similarity)

${displaystyle sigma }$

, that maps

${displaystyle c_{1}}$

onto

${displaystyle c_{2}}$

stretches (jolts) radius

${displaystyle r_{1}}$

to

${displaystyle r_{2}}$

and has its center

${displaystyle Z:{vec {z}}}$

on the line

${displaystyle {overline {M_{1}M_{2}}}}$

, because

${displaystyle sigma (M_{1})=M_{2}}$

. If center

${displaystyle Z}$

is between

${displaystyle M_{1},M_{2}}$

the scale factor is

${displaystyle s=-{tfrac {r_{2}}{r_{1}}}}$

. In the other case

${displaystyle s={tfrac {r_{2}}{r_{1}}}}$

. In any case:

${displaystyle sigma ({vec {m}}_{1})={vec {z}}+s({vec {m}}_{1}-{vec {z}})={vec {m}}_{2}}$

.

Inserting

${displaystyle s=pm {tfrac {r_{2}}{r_{1}}}}$

and solving for

${displaystyle {vec {z}}}$

yields:

${displaystyle {vec {z}}={frac {r_{1}{vec {m}}_{2}mp r_{2}{vec {m}}_{1}}{r_{1}mp r_{2}}}}$

.

Point

is called the exterior similarity point and

is called the inner similarity point.

In case of

${displaystyle M_{1}=M_{2}}$

one gets

${displaystyle E=I=M_{i}}$

.
In case of

${displaystyle r_{1}=r_{2}}$

:

${displaystyle E}$

is the point at infinity of line

${displaystyle {overline {M_{1}M_{2}}}}$

and

${displaystyle I}$

is the center of

${displaystyle M_{1},M_{2}}$

.
In case of

${displaystyle r_{1}=|EM_{1}|}$

the circles touch each other at point

${displaystyle E}$

inside (both circles on the same side of the common tangent line).
In case of

${displaystyle r_{1}=|IM_{1}|}$

the circles touch each other at point

${displaystyle I}$

outside (both circles on different sides of the common tangent line).

Further more:

• If the circles lie disjoint (the discs have no points in common), the outside common tangents meet at
  ${displaystyle E}$

  and the inner ones at

  ${displaystyle I}$

  .

• If one circle is contained within the other, the points
  ${displaystyle E,I}$

  lie within both circles.

• The pairs
  ${displaystyle M_{1},M_{2};E,I}$

  are projective harmonic conjugate: Their cross ratio is

  ${displaystyle (M_{1},M_{2};E,I)=-1}$

  .

Monge’s theorem states: The outer similarity points of three disjoint circles lie on a line.

Common power of two circles[edit]

Let

${displaystyle c_{1},c_{2}}$

be two circles,

${displaystyle E}$

their outer similarity point and

${displaystyle g}$

a line through

${displaystyle E}$

, which meets the two circles at four points

${displaystyle G_{1},H_{1},G_{2},H_{2}}$

. From the defining property of point

${displaystyle E}$

one gets

${displaystyle {frac {|EG_{1}|}{|EG_{2}|}}={frac {r_{1}}{r_{2}}}={frac {|EH_{1}|}{|EH_{2}|}} }$

${displaystyle rightarrow |EG_{1}|cdot |EH_{2}|=|EH_{1}|cdot |EG_{2}| }$

and from the secant theorem (see above) the two equations

${displaystyle |EG_{1}|cdot |EH_{1}|=Pi _{1}(E),quad |EG_{2}|cdot |EH_{2}|=Pi _{2}(E).}$

Combining these three equations yields:

Hence:

(independent of line

${displaystyle g}$

 !).
The analog statement for the inner similarity point

${displaystyle I}$

is true, too.

The invariants

${textstyle {sqrt {Pi _{1}(E)cdot Pi _{2}(E)}}, {sqrt {Pi _{1}(I)cdot Pi _{2}(I)}}}$

are called by Steiner common power of the two circles (gemeinschaftliche Potenz der beiden Kreise bezüglich ihrer Ähnlichkeitspunkte).^[6]

The pairs

${displaystyle G_{1},H_{2}}$

and

${displaystyle H_{1},G_{2}}$

of points are antihomologous points. The pairs

${displaystyle G_{1},G_{2}}$

and

${displaystyle H_{1},H_{2}}$

are homologous.^[7][8]

Determination of a circle that is tangent to two circles[edit]

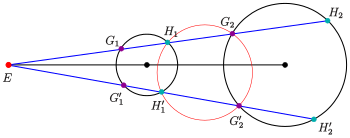
For a second secant through

${displaystyle E}$

:

${displaystyle |EH_{1}|cdot |EG_{2}|=|EH’_{1}|cdot |EG’_{2}|}$

From the secant theorem one gets:

The four points

${displaystyle H_{1},G_{2},H’_{1},G’_{2}}$

lie on a circle.

And analogously:

The four points

${displaystyle G_{1},H_{2},G’_{1},H’_{2}}$

lie on a circle, too.

Because the radical lines of three circles meet at the radical (see: article radical line), one gets:

The secants

${displaystyle {overline {H_{1}H’_{1}}},;{overline {G_{2}G’_{2}}}}$

meet on the radical axis of the given two circles.

Moving the lower secant (see diagram) towards the upper one, the red circle becomes a circle, that is tangent to both given circles. The center of the tangent circle is the intercept of the lines

${displaystyle {overline {M_{1}H_{1}}},{overline {M_{2}G_{2}}}}$

. The secants

${displaystyle {overline {H_{1}H’_{1}}},{overline {G_{2}G’_{2}}}}$

become tangents at the points

${displaystyle H_{1},G_{2}}$

. The tangents intercept at the radical line

${displaystyle p}$

(in the diagram yellow).

Similar considerations generate the second tangent circle, that meets the given circles at the points

${displaystyle G_{1},H_{2}}$

(see diagram).

All tangent circles to the given circles can be found by varying line

${displaystyle g}$

.

Positions of the centers

If

${displaystyle X}$

is the center and

${displaystyle rho }$

the radius of the circle, that is tangent to the given circles at the points

${displaystyle H_{1},G_{2}}$

, then:

${displaystyle rho =|XM_{1}|-r_{1}=|XM_{2}|-r_{2}}$

${displaystyle rightarrow |XM_{2}|-|XM_{1}|=r_{2}-r_{1}.}$

Hence: the centers lie on a hyperbola with

foci

${displaystyle M_{1},M_{2}}$

,

distance of the vertices^{[clarification needed]}

${displaystyle 2a=r_{2}-r_{1}}$

,

center

${displaystyle M}$

is the center of

${displaystyle M_{1},M_{2}}$

,

linear eccentricity

${displaystyle c={tfrac {|M_{1}M_{2}|}{2}}}$

and

${displaystyle b^{2}=e^{2}-a^{2}={tfrac {|M_{1}M_{2}|^{2}-(r_{2}-r_{1})^{2}}{4}}}$

^{[clarification needed]}.

Considerations on the outside tangent circles lead to the analog result:

If

${displaystyle X}$

is the center and

${displaystyle rho }$

the radius of the circle, that is tangent to the given circles at the points

${displaystyle G_{1},H_{2}}$

, then:

${displaystyle rho =|XM_{1}|+r_{1}=|XM_{2}|+r_{2}}$

${displaystyle rightarrow |XM_{2}|-|XM_{1}|=-(r_{2}-r_{1}).}$

The centers lie on the same hyperbola, but on the right branch.

See also Problem of Apollonius.

Power with respect to a sphere[edit]

The idea of the power of a point with respect to a circle can be extended to a sphere
.^[9] The secants and chords theorems are true for a sphere, too, and can be proven literally as in the circle case.

Darboux product[edit]

The power of a point is a special case of the Darboux product between two circles, which is given by^[10]

${displaystyle left|A_{1}A_{2}right|^{2}-r_{1}^{2}-r_{2}^{2},}$

where A₁ and A₂ are the centers of the two circles and r₁ and r₂ are their radii. The power of a point arises in the special case that one of the radii is zero.

If the two circles are orthogonal, the Darboux product vanishes.

If the two circles intersect, then their Darboux product is

${displaystyle 2r_{1}r_{2}cos varphi ,}$

where φ is the angle of intersection (see section orthogonal circle).

Laguerre’s theorem[edit]

Laguerre defined the power of a point P with respect to an algebraic curve of degree n to be the product of the distances from the point to the intersections of a circle through the point with the curve, divided by the nth power of the diameter d. Laguerre showed that this number is independent of the diameter (Laguerre 1905). In the case when the algebraic curve is a circle this is not quite the same as the power of a point with respect to a circle defined in the rest of this article, but differs from it by a factor of d².

References[edit]

• Coxeter, H. S. M. (1969), Introduction to Geometry (2nd ed.), New York: Wiley.
• Darboux, Gaston (1872), “Sur les relations entre les groupes de points, de cercles et de sphéres dans le plan et dans l’espace”, Annales Scientifiques de l’École Normale Supérieure, 1: 323–392, doi:10.24033/asens.87.
• Laguerre, Edmond (1905), Oeuvres de Laguerre: Géométrie (in French), Gauthier-Villars et fils, p. 20
• Steiner, Jakob (1826). “Einige geometrischen Betrachtungen” [Some geometric considerations]. Crelle’s Journal (in German). 1: 161–184. doi:10.1515/crll.1826.1.161. S2CID 122065577. Figures 8–26.
• Berger, Marcel (1987), Geometry I, Springer, ISBN 978-3-540-11658-5

Further reading[edit]

• Ogilvy C. S. (1990), Excursions in Geometry, Dover Publications, pp. 6–23, ISBN 0-486-26530-7
• Coxeter H. S. M., Greitzer S. L. (1967), Geometry Revisited, Washington: MAA, pp. 27–31, 159–160, ISBN 978-0-88385-619-2
• Johnson RA (1960), Advanced Euclidean Geometry: An elementary treatise on the geometry of the triangle and the circle (reprint of 1929 edition by Houghton Mifflin ed.), New York: Dover Publications, pp. 28–34, ISBN 978-0-486-46237-0

External links[edit]