Quadratic unconstrained binary optimization – Wikipedia
Quadratic unconstrained binary optimization (QUBO), also known as unconstrained binary quadratic programming (UBQP), is a combinatorial optimization problem with a wide range of applications from finance and economics to machine learning.[1] QUBO is an NP hard problem, and for many classical problems from theoretical computer science, like maximum cut, graph coloring and the partition problem, embeddings into QUBO have been formulated.[2][3]
Embeddings for machine learning models include support-vector machines, clustering and probabilistic graphical models.[4]
Moreover, due to its close connection to Ising models, QUBO constitutes a central problem class for adiabatic quantum computation, where it is solved through a physical process called quantum annealing.[5]
Definition[edit]
The set of binary vectors of a fixed length
, where
is the set of binary values (or bits).
We are given a real-valued upper triangular matrix
, whose entries
define a weight for each pair of indices
within the binary vector.
We can define a function
that assigns a value to each binary vector through
Intuitively, the weight
is added if both
and
have value 1.
When
, the values
are added if
, as
for all
.
The QUBO problem consists of finding a binary vector
that is minimal with respect to
, namely
In general,
is not unique, meaning there may be a set of minimizing vectors with equal value w.r.t.
.
The complexity of QUBO arises from the number of candidate binary vectors to be evaluated, as
grows exponentially in
.
Sometimes, QUBO is defined as the problem of maximizing
, which is equivalent to minimizing
.
Properties[edit]
- Multiplying the coefficients with a positive factor accordingly, leaving the optimum unchanged:
- Flipping the sign of all coefficients flips the sign of ‘s output, making the binary vector that maximizes :
- If all coefficients are positive, the optimum is trivially . Similarly, if all coefficients are negative, the optimum is .
- If , i.e., the bits can be optimized independently, then the corresponding QUBO problem is solvable in , the optimal variable assignments simply being 1 if and 0 otherwise.
Applications[edit]
QUBO is a structurally simple, yet computationally hard optimization problem.
It can be used to encode a wide range of optimization problems from various scientific areas.[6]
Cluster Analysis[edit]
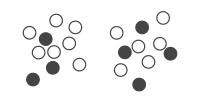
A bad cluster assignment.
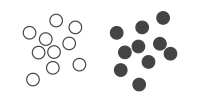
A good cluster assignment.
Visual representation of a clustering problem with 20 points: Circles of the same color belong to the same cluster. Each circle can be understood as a binary variable in the corresponding QUBO problem.
As an illustrative example of how QUBO can be used to encode an optimization problem, we consider the problem of cluster analysis.
Here, we are given a set of 20 points in 2D space, described by a matrix
, where each row contains two cartesian coordinates.
We want to assign each point to one of two classes or clusters, such that points in the same cluster are similar to each other.
For two clusters, we can assign a binary variable
to the point corresponding to the
-th row in
, indicating whether it belongs to the first (
) or second cluster (
).
Consequently, we have 20 binary variables, which form a binary vector
that corresponds to a cluster assignment of all points (see figure).
One way to derive a clustering is to consider the pairwise distances between points.
Given a cluster assignment
, the values
or
evaluate to 1 if points
and
are in the same cluster.
Similarly,
or
indicate that they are in different clusters.
Let
denote the Euclidean distance between points
and
.
In order to define a cost function to minimize, when points
and
are in the same cluster we add their positive distance
, and subtract it when they are in different clusters.
This way, an optimal solution tends to place points which are far apart into different clusters, and points that are close into the same cluster.
The cost function thus comes down to
From the second line, the QUBO parameters can be easily found by re-arranging to be:
Using these parameters, the optimal QUBO solution will correspond to an optimal cluster w.r.t. above cost function.
Connection to Ising models[edit]
QUBO is very closely related and computationally equivalent to the Ising model, whose Hamiltonian function is defined as
with real-valued parameters
for all
.
The spin variables
are binary with values from
instead of
.
Moreover, in the Ising model the variables are typically arranged in a lattice where only neighboring pairs of variables
can have non-zero coefficients.
Applying the identity
yields an equivalent QUBO problem:[2]
where
As the constant
does not change the position of the optimum
, it can be neglected during optimization and is only important for recovering the original Hamiltonian function value.
References[edit]
- ^ Kochenberger, Gary; Hao, Jin-Kao (2014). “The unconstrained binary quadratic programming problem: a survey” (PDF). Journal of Combinatorial Optimization. 28: 58–81. doi:10.1007/s10878-014-9734-0. S2CID 16808394.
- ^ a b Glover, Fred; Kochenberger, Gary (2019). “A Tutorial on Formulating and Using QUBO Models”. arXiv:1811.11538 [cs.DS].
- ^ Lucas, Andrew (2014). “Ising formulations of many NP problems”. Frontiers in Physics. 2: 5. arXiv:1302.5843. Bibcode:2014FrP…..2….5L. doi:10.3389/fphy.2014.00005.
- ^ Mücke, Sascha; Piatkowski, Nico; Morik, Katharina (2019). “Learning Bit by Bit: Extracting the Essence of Machine Learning” (PDF). LWDA. S2CID 202760166. Archived from the original (PDF) on 2020-02-27.
- ^ Tom Simonite (8 May 2013). “D-Wave’s Quantum Computer Goes to the Races, Wins”. MIT Technology Review. Retrieved 12 May 2013.
- ^ Ratke, Daniel (2021-06-10). “List of QUBO formulations”. Retrieved 2022-12-16.
External links[edit]
- QUBO Benchmark (Benchmark of software packages for the exact solution of QUBOs; part of the well-known Mittelmann benchmark collection)

 , where
, where  is the set of binary values (or bits).
is the set of binary values (or bits). , whose entries
, whose entries  define a weight for each pair of indices
define a weight for each pair of indices  within the binary vector.
within the binary vector. that assigns a value to each binary vector through
that assigns a value to each binary vector through

 and
and  have value 1.
have value 1. , the values
, the values  are added if
are added if  , as
, as  for all
for all  .
.
 that is minimal with respect to
that is minimal with respect to  , namely
, namely

 grows exponentially in
grows exponentially in  .
.
 .
.











 , where each row contains two cartesian coordinates.
, where each row contains two cartesian coordinates. -th row in
-th row in  , indicating whether it belongs to the first (
, indicating whether it belongs to the first ( ) or second cluster (
) or second cluster ( that corresponds to a cluster assignment of all points (see figure).
that corresponds to a cluster assignment of all points (see figure).
 , the values
, the values  or
or  evaluate to 1 if points
evaluate to 1 if points  are in the same cluster.
are in the same cluster. or
or  indicate that they are in different clusters.
indicate that they are in different clusters. denote the Euclidean distance between points
denote the Euclidean distance between points  , and subtract it when they are in different clusters.
, and subtract it when they are in different clusters.![{displaystyle {begin{aligned}f(x)&=sum _{i<j}d_{ij}(x_{i}x_{j}+(1-x_{i})(1-x_{j}))-d_{ij}(x_{i}(1-x_{j})+(1-x_{i})x_{j})\&=sum _{i<j}left[4d_{ij}x_{i}x_{j}-2d_{ij}x_{i}-2d_{ij}x_{j}+d_{ij}right]end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f46ef423537d3084fa6228aa3b293c924af3b5ac)


 for all
for all  .
. are binary with values from
are binary with values from  instead of
instead of  .
. can have non-zero coefficients.
can have non-zero coefficients. yields an equivalent QUBO problem:[2]
yields an equivalent QUBO problem:[2]

 does not change the position of the optimum
does not change the position of the optimum
Recent Comments