Toernooigraaf – Wikipedia

Een toernooigraaf, of alleen toernooi, in de grafentheorie is een complete graaf, waarin men aan elke kant een richting toewijst, zodat het een gerichte graaf wordt.

De naam “toernooigraaf” is afkomstig van de interpretatie van zo een graaf als het resultaat van competitievorm, waarin elke speler eenmaal tegen elke andere speler speelt en waarin geen gelijke spelen mogelijk zijn. Een kant ab in zo een graaf stelt een wedstrijd voor en is gericht van de winnaar a naar de verliezer b. Men zegt dan dat a b domineert en noteert dit als

${displaystyle arightarrow b}$

. De score van speler a is het aantal keer dat a heeft gewonnen, oftewel het aantal uitgaande kanten van a gericht naar andere spelers, oftewel het aantal andere spelers dat a domineert.

Toernooien zijn wellicht de best bestudeerde klasse van gerichte grafen.^[1]

Een toernooigraaf is een gerichte graaf

${displaystyle (V,E)}$

, waarvoor geldt:

• 
  ${displaystyle V}$

  heeft minimaal twee elementen

  ${displaystyle x}$

  en

  ${displaystyle y}$

  ,

• voor alle
  ${displaystyle x,yin V}$

  met

  ${displaystyle xnot =y}$

  geldt

  ${displaystyle (x,y)in E}$

  of

  ${displaystyle (y,x)in E}$

  ,

• voor alle
  ${displaystyle x,yin V}$

  met

  ${displaystyle xnot =y}$

  geldt

  ${displaystyle (x,y)not in E}$

  of

  ${displaystyle (y,x)not in E}$

  ,

• voor alle
  ${displaystyle xin V}$

  geldt

  ${displaystyle (x,x)not in E}$

  .

Men kan een toernooi ook definiëren als een tweeplaatsige relatie

${displaystyle R}$

op een verzameling

${displaystyle E}$

die irreflexief, antisymmetrisch en totaal is. Dat wil zeggen dat voor elk paar

${displaystyle (x,y)}$

elementen uit

${displaystyle E}$

geldt: ofwel

${displaystyle x=y}$

, ofwel

${displaystyle x R y}$

, ofwel

${displaystyle y R x}$

.

Elke eindige toernooigraaf met

${displaystyle n}$

knopen bevat een oneven aantal Hamiltonpaden. Een Hamiltonpad is een gericht pad langs alle

${displaystyle n}$

knopen.

Dat betekent dat er in elke toernooigraaf ten minste één Hamiltonpad voorkomt. Dit laatste kan met volledige inductie naar het aantal knopen

${displaystyle n}$

van de toernooigraaf worden bewezen.

• Het inductiebegin, voor het geval
  ${displaystyle n=2}$

  , wijst zich vanzelf.

  ${displaystyle x}$

  heeft of gewonnen of verloren van

  ${displaystyle y}$

  , het Hamiltonpad wijst van de winnaar naar de verliezer.

• De inductieveronderstelling is dat de stelling waar is voor een toernooigraaf met
  ${displaystyle n}$

  knopen.

• De inductiestap gaat als volgt. Veronderstel dat in een toernooi alle wedstrijden zijn gespeeld en er in de toernooigraaf een Hamilton-pad is. Dat is gegeven. Wanneer een nieuwe speler een keer tegen alle eerdere spelers speelt, krijgt deze nieuwe speler zijn plaats tussen het Hamilton-pad van de andere, de eerste spelers.

Beschouw de toernooigraaf

${displaystyle T}$

met

${displaystyle n+1}$

knopen. Kies een knoop

${displaystyle v_{0}}$

in

${displaystyle T}$

en beschouw een gericht pad

${displaystyle v_{1},v_{2},ldots ,v_{n}}$

in

${displaystyle Tsetminus {v_{0}}}$

. Stel

${displaystyle iin {0,ldots ,n}}$

de grootste index zodat voor elke

${displaystyle jleq i}$

er een gerichte kant is van

${displaystyle v_{j}}$

naar

${displaystyle v_{0}}$

.

Als

${displaystyle i=n}$

, dan is

${displaystyle v_{1},v_{2},ldots ,v_{n},v_{0}}$

een Hamiltonpad van

${displaystyle T}$

.

Als

${displaystyle i$

, dan is

${displaystyle v_{1},ldots ,v_{i},v_{0},v_{i+1},ldots ,v_{n}}$

een Hamiltonpad van

${displaystyle T}$

.

Het feit dat er een gerichte kant van

${displaystyle v_{0}}$

naar

${displaystyle v_{i+1}}$

gaat volgt uit het feit dat

${displaystyle i}$

de grootste index is zodat er voor elke

${displaystyle jleq i}$

een kant van

${displaystyle v_{j}}$

naar

${displaystyle v_{0}}$

gaat.

Een toernooi is sterk of sterk verbonden indien er tussen elk paar knopen x en y een pad bestaat dat begint in x en eindigt in y. Een stelling van Paul Camion uit 1959 stelt dat een toernooi sterk verbonden is dan en slechts dan als het toernooi een Hamiltoncykel, een gesloten Hamiltonpad, bezit. Wanneer a van b wint en b van c wint, is het in een sterk toernooi niet zeker dat a ook van c wint. Met maar drie spelers is het juist alleen een sterk toernooi, wanneer c van a wint.

De knopen in een sterk toernooi heten pancyclisch: iedere knoop

${displaystyle v}$

van een sterk toernooi behoort tot een cykel, een gesloten pad, van lengte

${displaystyle k}$

voor

${displaystyle k=3,4,dots ,n}$

, met

${displaystyle ngeq 3}$

het aantal knopen in de graaf.

S(n), het aantal verschillende sterke toernooien met n knopen, met n = 3, 4, 5, 6, 7, 8, … is 2, 24, 544, 22320, 1677488, 236522496, … ,^[2] rij A054946 in OEIS.

Een toernooi waarvoor steeds geldt dat als a van b wint en b van c wint, a ook van c wint, is een transitief toernooi. In het toernooi heerst een totale orde. De figuur hiernaast is een voorbeeld van een transitief toernooi.

Formeel wordt een transitief toernooi gedefinieerd als

Toernooi

${displaystyle T=(V,E)}$

is transitief als

${displaystyle forall (a,b,c)in V^{3},(arightarrow b{text{ en }}brightarrow c)Rightarrow arightarrow c}$

In een transitief toernooi komt precies één Hamiltonpad voor. Een transitief toernooi bevat geen cykels. Het is het tegenovergestelde van een sterk toernooi.

De scores van de deelnemers aan een transitief toernooi, gerangschikt van klein naar groot, is de verzameling {0,1,2,…,n − 1}.

In een transitief toernooi is er een deelnemer die al zijn wedstrijden wint. In echte competities komt dit maar weinig voor. Het voorbeeld in de figuur met 4 deelnemers hierboven is bijvoorbeeld geen transitief toernooi. Een toernooi waarin elke speler minstens eenmaal verliest noemt men een 1-paradoxaal toernooi.

In het algemeen is een toernooi k-paradoxaal als voor elke deelverzameling S met k elementen uit V er voor alle knopen v in S er k andere knopen

${displaystyle v_{i}}$

in

${displaystyle Vsetminus S}$

zijn, zo dat

${displaystyle v_{i}rightarrow v}$

.

Een toernooi is gelijkmatig als elke knoop evenveel inkomende als uitgaande kanten heeft, dit zijn grafen met een Euleriaanse oriëntatie. Een gelijkmatig toernooi heeft per definitie een oneven aantal deelnemers of knopen, die alle dezelfde score hebben. Het aantal verschillende gelijkmatige toernooien met 3, 5, 7, 9, 11… deelnemers is: 1, 1, 3, 15, 1223… rij A096368 in OEIS.

Alle gelijkmatige toernooien met hetzelfde aantal deelnemers hebben evenveel driehoeken en evenveel transitieve tripels. Een driehoek is een reeks van drie kanten (x,y), (y,z), (z,x) die een cykel vormen, een transitieve tripel bestaat uit drie kanten van de vorm (x,y), (y,z), (x,z).

Het aantal transitieve tripels in een gelijkmatig toernooi met n knopen is

${displaystyle {frac {n(n-1)(n-3)}{8}}}$

. Het aantal driehoeken is

${displaystyle {frac {n(n^{2}-1)}{24}}}$

.^[3]

Voorbeeld[bewerken | brontekst bewerken]

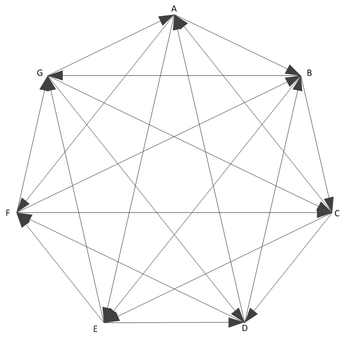
Dit is een voorbeeld van een gelijkmatig toernooi met 7 deelnemers, elke knoop heeft drie in- en drie uitgaande kanten. Er zijn 21 kanten, dat zijn de pijlen in de graaf, 14 driehoeken, bijvoorbeeld AF-FC-CA, en 21 transitieve tripels, bijvoorbeeld CE-ED-CD.

Men noemt een toernooi reduceerbaar als de verzameling V van knopen kan worden gesplitst in twee disjuncte toernooigrafen S en T, waarbij iedere knoop uit S iedere knoop uit T domineert. V = S + T, met

${displaystyle Srightarrow T}$

. Als dit niet mogelijk is, dan is het toernooi niet-reduceerbaar.

Een toernooi is niet-reduceerbaar dan en slechts dan als het sterk is verbonden. Een transitief toernooi is reduceerbaar. Het hierboven gegeven voorbeeld met 8 knopen kan men bijvoorbeeld splitsen in twee toernooien met respectievelijk de knopenverzamelingen {1,2,3} en {4,5,6,7,8}, of {1,2,3,4} en {5,6,7,8}, enzovoort. Ieder toernooi kan worden geschreven als de som van één of meer niet-reduceerbare toernooien. De deelnemers zijn dan te verdelen in groepen spelers, die ongeveer even goed zijn. Tussen de verschillende groepen spelers zijn wel duidelijke verschillen.

De score van een deelnemer aan een toernooi is het aantal door hem gewonnen wedstrijden. Dit is het aantal uitgaande kanten van een knoop in de toernooigraaf.

De scoreverzameling is de verzameling van het aantal uitgaande kanten van alle knopen. Het is eenvoudig om de scoreverzameling van een toernooi te bepalen, maar een toernooi construeren aan de hand van een gegeven scoreverzameling is een moeilijk probleem. De score-rij of scorevector is de geordende rij van scores of aantal uitgaande kanten, gerangschikt van klein naar groot.

De stelling van Landau^[4] zegt dat een rij

${displaystyle s_{1},s_{2},cdots ,s_{n}}$

van niet-negatieve gehele getallen een score-rij is dan en slechts dan als:

1. 
   ${displaystyle 0leq s_{1}leq s_{2}leq cdots leq s_{n}}$

   

2. 
   ${displaystyle s_{1}+s_{2}+cdots +s_{i}geq C_{i}^{2},{mbox{voor }}i=1,2,cdots ,n-1}$

   

3. 
   ${displaystyle s_{1}+s_{2}+cdots +s_{n}=C_{n}^{2}}$

   

${displaystyle C_{n}^{2}}$

is gelijk aan het totaal aantal kanten in de toernooigraaf.

Verschillende toernooien kunnen dezelfde score-rij hebben. Peter M. Gibson leidde in 1983 een uitdrukking af voor de bovengrens van het aantal toernooien met een gegeven score-rij, of scorevector.^[5]

Het aantal mogelijke verschillende score-rijen van toernooien met n = 0, 1, 2, 3, … deelnemers is, rij A000571 in OEIS, 1, 1, 1, 2, 4, 9, 22, 59, 167, 490, 1486, 4639, 14805, 48107, …

T.X. Yao^[6] heeft bewezen dat elke willekeurige eindige verzameling van niet-negatieve gehele getallen de scoreverzameling van een zeker toernooi is. K.B. Reid had dit als een vermoeden in 1978 geformuleerd.

De resultaten van een toernooi kunnen ook met een matrix worden weergegeven:

1 wanneer

${displaystyle v_{i}rightarrow v_{j}}$

-1 wanneer

${displaystyle v_{j}rightarrow v_{i}}$

0 wanneer het resultaat tussen i en j nog niet bekend is en wanneer i=j.

De elementen op de diagonaal blijven 0.

Een dergelijke matrix A is een antisymmetrische matrix: de getransponeerde matrix van A is gelijk aan het tegengestelde van A:

${displaystyle A^{T}=-A}$

De definitie van een toernooi is zo gekozen, dat het volledig is gespeeld. De toernooimatrix van het toernooi met vier deelnemers in de figuur boven, wordt:

${displaystyle {begin{bmatrix}0&1&-1&1\-1&0&-1&1\1&1&0&-1\-1&-1&1&0end{bmatrix}}}$

Bronnen, noten en/of referenties ↑ Jǿrgen Bang-Jensen, Gregory Gutin. “Generalizations of Tournaments: A Survey.” Journal of Graph Theory, 1998, Vol. 28 nr. 4, p. 171 DOI:10.1002/(SICI)1097-0118(199808)28:4<171::AID-JGT1>3.0.CO;2-G ↑ Denis Hanson, John W. Moon. “Weakening Arcs in Tournaments.” Journal of Graph Theory, 2003, vol. 45 nr. 2, blz. 142 DOI:10.1002/jgt.10148 ↑ Raphael Yuster. “Packing Triangles in Regular Tournaments.” Journal of Graph Theory, 2013, vol. 74 nr. 1, blz. 58-66. DOI:10.1002/jgt.21691 ↑ H. G. Landau, “On dominance relations and the structure of animal societies. III. The condition for a score structure”, Bulletin of Mathematical Biophysics, vol. 15, no 2, 1953, p. 143–148. DOI:10.1007/BF02476378 ↑ Peter M. Gibson. “A bound for the number of tournaments with specified scores.” Journal of Combinatorial Theory, Series B 1984, Vol. 36, blz. 240-243. DOI:10.1016/0095-8956(84)90030-3 ↑ T. X. Yao, “On Reid Conjecture Of Score Sets For Tournaments”, Chinese Sci. Bull., vol. 34, 1989, p. 804−808