Rationale Trigonometrie – Wikipedia

Posted on December 16, 2020 by lordneo

before-content-x4

Rationale Trigonometrie ist eine vorgeschlagene Neuformulierung metrischer planarer und fester Geometrien (einschließlich Trigonometrie) des kanadischen Mathematikers Norman J. Wildberger, der derzeit Professor für Mathematik an der University of New South Wales ist. Seine Ideen sind in seinem Buch von 2005 dargelegt Göttliche Proportionen: Rationale Trigonometrie zur universellen Geometrie.^[1] Gemäß Neuer WissenschaftlerEin Teil seiner Motivation für eine Alternative zur traditionellen Trigonometrie bestand darin, einige Probleme zu vermeiden, von denen er behauptet, dass sie auftreten, wenn in der Mathematik unendliche Reihen verwendet werden. Die rationale Trigonometrie vermeidet die direkte Verwendung transzendentaler Funktionen wie Sinus und Cosinus, indem sie ihre quadratischen Äquivalente ersetzt.^[2] Wildberger lässt sich von Mathematikern inspirieren, die vor Georg Cantors Theorie der unendlichen Mengen existierten, wie Gauß und Euklid, von denen er behauptet, dass sie bei der Verwendung unendlicher Mengen weitaus vorsichtiger waren als moderne Mathematiker.^[2]^{[nb 1]} Bis heute wird die rationale Trigonometrie in der gängigen mathematischen Literatur weitgehend nicht erwähnt.

Table of Contents

Ansatz[edit]

Die rationale Trigonometrie folgt einem Ansatz, der auf den Methoden der linearen Algebra zu den Themen der Grundgeometrie (High School Level) basiert. Die Entfernung wird durch ihren quadratischen Wert ersetzt (Quadranz) und ‘Winkel’ wird durch den Quadratwert des üblichen Sinusverhältnisses (Ausbreitung) einem Winkel zwischen zwei Linien zugeordnet. (Das Komplement von Spread, bekannt als Kreuzentspricht auch einer skalierten Form des inneren Produkts zwischen Liniensegmenten als Vektoren). Die drei Hauptgesetze der Trigonometrie – der Satz von Pythagoras, das Sinusgesetz und das Kosinusgesetz – werden in rationaler (quadratisch äquivalenter) Form angegeben und durch zwei weitere Gesetze ergänzt – die Dreifach-Quad-Formel (die die Quadranzen von drei kollinearen Punkten in Beziehung setzt) und die Triple-Spread-Formel (die die Spreads von drei gleichzeitigen Linien in Beziehung setzt) - unter Angabe der fünf Hauptgesetze des Subjekts.^{[citation needed]}

Die rationale Trigonometrie basiert ansonsten weitgehend auf der kartesischen analytischen Geometrie mit ein Punkt definiert als ein geordnetes Paar rationaler Zahlen

{ displaystyle (x, y)}

und eine Linie

{ displaystyle axe + by + c = 0,}

als allgemeine lineare Gleichung mit rationalen Koeffizienten $ein$ , $b$ und $c$ .

Indem Sie Berechnungen vermeiden, die nur auf Quadratwurzeloperationen beruhen ungefähr Abstände zwischen Punkten oder standardmäßige trigonometrische Funktionen (und ihre Umkehrungen), die nur abgeschnittenes Polynom ergeben Annäherungen der Geometrie der Winkel (oder ihrer Projektionen) wird vollständig algebraisch. Mit anderen Worten, es gibt keine Annahme, dass es reelle Zahlenlösungen für Probleme gibt, deren Ergebnisse stattdessen über das Feld der rationalen Zahlen, ihre algebraischen Felderweiterungen oder endlichen Felder gegeben werden. Im Anschluss daran, so wird behauptet, sind viele klassische Ergebnisse der euklidischen Geometrie in anwendbar rational Form (als quadratische Analoga) über jedem Feld, das nicht charakteristisch zwei ist.^{[citation needed]}

Das Buch Göttliche Proportionen zeigt die Anwendung der Analysis unter Verwendung rationaler trigonometrischer Funktionen, einschließlich dreidimensionaler Volumenberechnungen. Es befasst sich auch mit der Anwendung der rationalen Trigonometrie auf Situationen mit Irrationalen, wie dem Beweis, dass alle platonischen Festkörper rationale „Ausbreitungen“ zwischen ihren Gesichtern haben.^{[nb 2]}

Bemerkbarkeit und Kritik[edit]

Rationale Trigonometrie (RT) wird neben Wildbergers eigenen Artikeln und Büchern nur in einer bescheidenen Anzahl mathematischer Veröffentlichungen erwähnt. Göttliche Proportionen wurde von Rezensent Paul J. Campbell in der entlassen Mathematik-Magazin der Mathematical Association of America (MAA): “Der Autor behauptet, dass diese neue Theorie ‘weniger als die Hälfte der üblichen Zeit zum Lernen benötigt’; aber ich bezweifle es. Und sie müsste immer noch mit den traditionellen Konzepten und der Notation verbunden werden.” . ” Der Rezensent William Barker, Isaac Henry Wing Professor für Mathematik am Bowdoin College, der ebenfalls für die MAA schrieb, war eher einverstanden: “Göttliche Proportionen ist zweifellos eine wertvolle Ergänzung zur mathematischen Literatur. Es entwickelt sorgfältig einen zum Nachdenken anregenden, klugen und nützlichen alternativen Ansatz für Trigonometrie und euklidische Geometrie. Es wäre nicht überraschend, wenn einige seiner Methoden letztendlich in die Standardentwicklung dieser Themen einfließen würden. Sofern sich die akzeptierten Ansichten über die Grundlagen der Mathematik nicht unerwartet verschieben, gibt es keinen starken Grund dafür, dass die rationale Trigonometrie die klassische Theorie ersetzt. ” ^[3]Neuer Wissenschaftler ‘s Amanda Gefter beschrieb den Ansatz von Wildberger als Beispiel für Finitismus.^[2]James Franklin in der Mathematischer Intelligencer argumentierte, dass das Buch eine sorgfältige Prüfung verdient.^[4]

Eine Analyse von Michael Gilsdorf zu den Beispielproblemen, die Wildberger in einem frühen Artikel gegeben hatte, bestritt die Behauptung, dass RT erforderte weniger Schritte zu lösen die meisten Probleme, wenn die freie Auswahl klassischer Methoden (wie die ‘Schnürsenkelformel’ für die Fläche eines Dreiecks aus den Koordinaten seiner Eckpunkte oder die direkte Anwendung eines Sonderfalls des Stewartschen Theorems auf ein Dreieck mit einem Median) die Lösung optimieren darf von Problemen. In Bezug auf die Pädagogik und ob die quadratischen Größen verwendet werden von RT Der Autor stellte fest, dass die klassische Trigonometrie ursprünglich nicht auf der Verwendung von Taylor-Reihen zur Approximation von Winkeln beruhte, sondern auf Messungen der Sehne (doppelt so hoch wie der Sinus eines Winkels) und somit mit einem angemessenen Verständnis der Schüler Nutzen Sie die Vorteile der linearen Messung ohne die beanspruchten Vorteile logisch Inkonsistenzen, wenn anschließend eine kreisförmige Parametrisierung nach Winkel eingeführt wird.^[5]

Quadrance[edit]

Der euklidische Abstand und der quadratische euklidische Abstand (in der rationalen Trigonometrie als “Quadranz” bezeichnet) messen beide die Trennung von Punkten im euklidischen Raum.^[6] Nach dem Satz von Pythagoras das Quadranten zweier Punkte $EIN 1 = (x 1, y 1)$ und $EIN 2 = (x 2, y 2)$ in einer Ebene ist daher definiert als die Summe der Quadrate der Differenzen in der

{ displaystyle x}

$x$ und

{ displaystyle y}

$y$ Koordinaten:

{ displaystyle Q (A_ {1}, A_ {2}) = (x_ {2} -x_ {1}) ^ {2} + (y_ {2} -y_ {1}) ^ {2}.}

Die Dreiecksungleichung

{ displaystyle d_ {3} leq d_ {1} + d_ {2}}

${ displaystyle d_ {3} leq d_ {1} + d_ {2}}$ wird unter rationaler Trigonometrie ausgedrückt als

{ displaystyle (Q_ {3} -Q_ {1} -Q_ {2}) ^ {2} leq 4Q_ {1} Q_ {2}}

${ displaystyle (Q_ {3} -Q_ {1} -Q_ {2}) ^ {2} leq 4Q_ {1} Q_ {2}}$ .

Annehmen

l 1

und

l 2

am Punkt schneiden

EIN

. Lassen

C.

sei der Fuß der Senkrechten von

B.

l 2

. Dann ist die Verbreitung

s = Q. /. R.

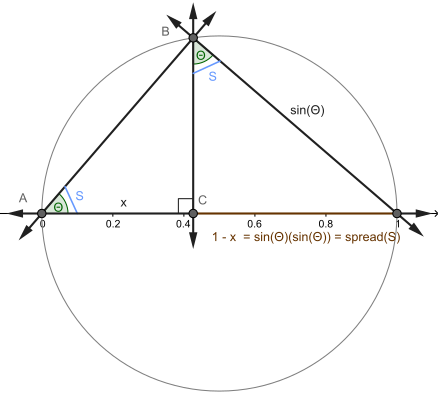
Die Streuung gibt ein Maß für die Trennung zweier Linien als einzelne dimensionslose Zahl im Bereich $[0,1]$ (von parallel zu aufrecht) für die euklidische Geometrie. Es ersetzt das im folgenden Abschnitt beschriebene Konzept des Winkels (und weist mehrere Unterschiede zu diesem auf). Beschreibungen der Verbreitung können umfassen:

Trigonometrisch (elementarste): die Sinusverhältnis von Quadranzen in einem rechtwinkligen Dreieck, entsprechend dem Quadrat des Sinus des Winkels (links).^[6] Durch Ausdehnung der angrenzenden Seite $AC$ Teil der Einheit Durchmesser in einem Kreis und unter Berücksichtigung ähnlicher Dreiecke (Recht) kann die Ausbreitung als gemessen werden Länge (oder Verhältnis zum Durchmesser) des äußeren Segments – traditionell gleich dem halben Mal (1 minus dem Kosinus des doppelten Winkels bei $EIN$ ) oder haversine.
Vektor: als rationale Funktion der Pisten (und relativ Richtung) eines Paares von Linien, wo sie sich treffen.
Kartesisch: als rationale Funktion von drei Koordinaten verwendet, um zuzuschreiben zwei Vektoren.
Lineare Algebra (von dem Skalarprodukt): eine normalisierte rationale Funktion: die Quadrat von die Determinante von zwei Vektoren (oder einem Paar sich schneidender Linien), die eine Matrix bilden, geteilt durch das Produkt ihrer Quadranzen.

Spread berechnen[edit]

Trigonometrisch[edit]

Angenommen, zwei Zeilen, $l 1$ und $l 2$ schneiden sich am Punkt $EIN$ wie rechts gezeigt. Wähle einen Punkt $B. \neq EIN$ auf $l 1$ und lass $C.$ sei der Fuß der Senkrechten von $B.$ zu $l 2$ . Dann die Ausbreitung $s$ ist^[6]

{ displaystyle s ( ell _ {1}, ell _ {2}) = { frac {Q (B, C)} {Q (A, B)}} = { frac {Q} {R} }.}

Vektor / Steigung (zwei Variablen)[edit]

Wie der Winkel hängt die Streuung nur von den relativen Steigungen zweier Linien ab (konstante Terme werden eliminiert) und ist bei der Translation unveränderlich (dh sie bleibt erhalten, wenn Linien parallel zu sich selbst bewegt werden). Also zwei Linien gegeben, deren Gleichungen sind

{ displaystyle a_ {1} x + b_ {1} y = { text {Konstante}} qquad { text {und}} qquad a_ {2} x + b_ {2} y = { text {Konstante }}}

wir können sie als zwei Zeilen umschreiben, die sich am Ursprung treffen $(0, 0)$ mit Gleichungen

{ displaystyle a_ {1} x + b_ {1} y = 0 qquad { text {und}} qquad a_ {2} x + b_ {2} y = 0}

In dieser Position der Punkt $(- b 1, ein 1)$ erfüllt die erste Gleichung und $(- b 2, ein 2)$ erfüllt den zweiten und die drei Punkte $(0, 0)$ , $(- b 1, ein 1)$ und $(- b 2, ein 2)$ Das Bilden des Spread ergibt drei Quadranzen:

{ displaystyle { begin {align} Q_ {1} & = left (b_ {1} ^ {2} + a_ {1} ^ {2} right), \ Q_ {2} & = left ( b_ {2} ^ {2} + a_ {2} ^ {2} rechts), \ Q_ {3} & = links (b_ {1} -b_ {2} rechts) ^ {2} + left (a_ {1} -a_ {2} right) ^ {2} end {align}}}

Das Cross Law – siehe unten – in Bezug auf die Verbreitung ist

{ displaystyle 1-s = { frac {(Q_ {1} + Q_ {2} -Q_ {3}) ^ {2}} {4Q_ {1} Q_ {2}}}.}

was wird:

{ displaystyle 1-s = { frac { left (a_ {1} ^ {2} + a_ {2} ^ {2} + b_ {1} ^ {2} + b_ {2} ^ {2} – (b_ {1} -b_ {2}) ^ {2} – (a_ {1} -a_ {2}) ^ {2} rechts) ^ {2}} {4 links (a_ {1} ^ { 2} + b_ {1} ^ {2} rechts) links (a_ {2} ^ {2} + b_ {2} ^ {2} rechts)}}.}

Dies vereinfacht im Zähler zu $(2 ein 1 ein 2 + 2 b 1 b 2) 2$ , geben:

{ displaystyle 1-s = { frac { left (a_ {1} a_ {2} + b_ {1} b_ {2} right) ^ {2}} { left (a_ {1} ^ {2 } + b_ {1} ^ {2} rechts) links (a_ {2} ^ {2} + b_ {2} ^ {2} rechts)}}.}

(Hinweis: $1 - s$ ist der Ausdruck für die Kreuz, das Quadrat des Kosinus eines Winkels zwischen einem Paar von Linien oder Vektoren, das dem Namen gibt Cross Law.)

Dann unter Verwendung der Brahmagupta-Fibonacci-Identität

{ displaystyle left (a_ {2} b_ {1} -a_ {1} b_ {2} right) ^ {2} + left (a_ {1} a_ {2} + b_ {1} b_ {2 } rechts) ^ {2} = links (a_ {1} ^ {2} + b_ {1} ^ {2} rechts) links (a_ {2} ^ {2} + b_ {2} ^ { 2} right),}

Der Standardausdruck für die Streuung in Bezug auf Steigungen (oder Richtungen) von zwei Linien wird

{ displaystyle s = { frac { left (a_ {1} b_ {2} -a_ {2} b_ {1} right) ^ {2}} { left (a_ {1} ^ {2} + b_ {1} ^ {2} rechts) links (a_ {2} ^ {2} + b_ {2} ^ {2} rechts)}}.}

In dieser Form (und in ihrem folgenden kartesischen Äquivalent) ist ein Spread das Verhältnis des Quadrats einer Determinante zweier Vektoren (Zähler) zum Produkt ihrer Quadranzen (Nenner).

Kartesisch (drei Variablen)[edit]

Für ein Dreieck können wir im Gegensatz zu einem Linien- oder Vektorpaar Punkte ersetzen $(- b 1, ein 1)$ , $(- b 2, ein 2)$ und $‘(0, 0)’$ im vorherigen Ergebnis mit $((x 1, y 1)$ , $((x 2, y 2)$ und $((x 3, y 3)$ um die Ausbreitung an einem geeigneten Scheitelpunkt zu erhalten:

{ displaystyle s_ {3} = { frac {{ bigl (} (y_ {1} -y_ {3}) (x_ {2} -x_ {3}) – (y_ {2} -y_ {3} ) (x_ {1} -x_ {3}) { bigr)} ^ {2}} {{ bigl (} (y_ {1} -y_ {3}) ^ {2} + (x_ {1} – x_ {3}) ^ {2} { bigr)} { bigl (} (y_ {2} -y_ {3}) ^ {2} + (x_ {2} -x_ {3}) ^ {2} { bigr)}}}.}

was in symmetrischer Zählerform wird:

{ displaystyle s_ {3} = { frac {{ bigl (} (y_ {1} x_ {2} -y_ {2} x_ {1}) + (y_ {2} x_ {3} -y_ {3 } x_ {2}) + (y_ {3} x_ {1} -y_ {1} x_ {3}) { bigr)} ^ {2}} {{ bigl (} (y_ {1} -y_ { 3}) ^ {2} + (x_ {1} -x_ {3}) ^ {2} { bigr)} { bigl (} (y_ {2} -y_ {3}) ^ {2} + ( x_ {2} -x_ {3}) ^ {2} { bigr)}}},}

und daher für die anderen damit verbundenen Spreads, s₁ und s₂::

{ displaystyle s_ {2} = { frac {{ bigl (} (y_ {1} x_ {2} -y_ {2} x_ {1}) + (y_ {2} x_ {3} -y_ {3 } x_ {2}) + (y_ {3} x_ {1} -y_ {1} x_ {3}) { bigr)} ^ {2}} {{ bigl (} (y_ {1} -y_ { 2}) ^ {2} + (x_ {1} -x_ {2}) ^ {2} { bigr)} { bigl (} (y_ {3} -y_ {2}) ^ {2} + ( x_ {3} -x_ {2}) ^ {2} { bigr)}}},}

{ displaystyle s_ {1} = { frac {{ bigl (} (y_ {1} x_ {2} -y_ {2} x_ {1}) + (y_ {2} x_ {3} -y_ {3 } x_ {2}) + (y_ {3} x_ {1} -y_ {1} x_ {3}) { bigr)} ^ {2}} {{ bigl (} (y_ {3} -y_ { 1}) ^ {2} + (x_ {3} -x_ {1}) ^ {2} { bigr)} { bigl (} (y_ {2} -y_ {1}) ^ {2} + ( x_ {2} -x_ {1}) ^ {2} { bigr)}}}.}

Spread im Vergleich zum Winkel[edit]

Die Streuung zweier Linien kann an vier äquivalenten Positionen gemessen werden.

Im Gegensatz zu Winkel, der eine Beziehung zwischen definieren kann Strahlen Ausgehend von einem Punkt, durch eine Bogenmessungsparametrisierung, und wo ein Linienpaar als vier Strahlenpaare betrachtet werden kann, die vier Winkel bilden, ist die “Ausbreitung” in der rationalen Trigonometrie grundlegender und beschreibt zwei Linien durch ein einzelnes Maß einer rationalen Funktion (siehe oben).^[6] Gleichwertig sein mit dem Quadrat eines Sinus des entsprechenden Winkels $θ$ (und zum Haversine des akkordbasierten Doppelwinkels $Δ = 2 θ$ ) sind die Streuung sowohl eines Winkels als auch seines Zusatzwinkels gleich.

Ausbreitung	Winkel ( $θ$ )					Menge
$Sünde 2 ((θ)$	Quadranten	Wendet sich	Bogenmaß	Grad	Gons	Einheit
0	0	0	0	0 °	0^G
1/.4	1/.3	1/.12	$π$ /.6	30 °	33+1/.3^G
1/.2	1/.2	1/.8	$π$ /.4	45 °	50^G
3/.4	2/.3	1/.6	$π$ /.3	60 °	66+2/.3^G
1	1	1/.4	$π$ /.2	90 °	100^G	orthogonale Linien
3/.4	1+1/.3	1/.3	2 $π$ /.3	120 °	133+1/.3^G
1/.2	1+1/.2	3/.8	3 $π$ /.4	135 °	150^G
1/.4	1+2/.3	5/.12	5 $π$ /.6	150 °	166+2/.3^G
0	2	1/.2	$π$	180 °	200^G

Die Ausbreitung ist jedoch nicht proportional zum Abstand zwischen den Linien, wie es der Winkel wäre; mit Spreads von 0, 1/.4, 1/.2, 3/.4und 1 entsprechend ungleichmäßig beabstandeten Winkeln 0 °, 30 °, 45 °, 60 ° und 90 °.

Stattdessen bestimmen (unter Hinweis auf die ergänzende Eigenschaft) zwei gleiche, co-terminale Spreads einen dritten Spread, dessen Wert eine Lösung der Triple-Spread-Formel für ein Dreieck (oder drei gleichzeitige Linien) mit Spreads von ist $s$ , $s$ und $r$ ::

{ displaystyle { begin {align} (2s + r) ^ {2} & = 2 left (2s ^ {2} + r ^ {2} right) + 4s ^ {2} r \ 4s ^ { 2} + 4sr + r ^ {2} & = 4s ^ {2} + 2r ^ {2} + 4s ^ {2} r end {align}}}

Geben des quadratischen Polynoms (in $s$ ):

{ displaystyle { begin {align} r ^ {2} + 4s ^ {2} r-4sr & = 0 \ r ^ {2} -4s (1-s) r & = 0 end {align}}}

und Lösungen

{ displaystyle r = 0 quad ({ text {trivial}}) qquad { text {oder}} qquad r = 4s (1-s)}

Dies entspricht der trigonometrischen Identität:

{ displaystyle sin ^ {2} (2 theta) = 4 sin ^ {2} theta left (1- sin ^ {2} theta right)}

der Winkel $θ$ , $θ$ und $180 ° - 2 θ$ eines Dreiecks mit

{ displaystyle S_ {2} (s) = S_ {2} left ( sin ^ {2} theta right) = sin ^ {2} (2 theta) = r (s)}

a zweite Polynom verbreiten in $s$ .

Das Finden des Tripels eines Spreads verwendet ebenfalls die Triple-Spread-Formel als quadratische Gleichung im unbekannten dritten Spread $t$ Behandlung der bekannten Aufstriche $s$ und $r$ (die vorherige Lösung) als Konstanten. Dies stellt sich heraus (nach Eliminierung der “kleineren” Lösung $s$ ) sein:

{ displaystyle S_ {3} (s) = s (3-4s) ^ {2} = t (s)}

Weitere Vielfache einer Grundstreuung von Linien können entweder durch fortgesetzte Verwendung der Dreifachstreuungsformel auf diese Weise oder durch Verwendung einer Rekursionsformel (siehe unten) erzeugt werden, die sie indirekt anwendet. Während ein Vielfaches eines rationalen Spreads in diesem Spread polynomisch (und daher rational) ist, gilt das Gegenteil nicht. Beispielsweise haben nach der Halbwinkelformel zwei Linien, die sich in einem Winkel von 15 ° (oder 165 °) treffen, eine Streuung von:

{ displaystyle operatorname {hav} left (30 ^ { circ} right) = sin ^ {2} left ({ frac {30 ^ { circ}} {2}} right) = { frac {1- cos 30 ^ { circ}} {2}} = { frac {1 – { frac { sqrt {3}} {2}} {2}} = { frac {2 – { sqrt {3}}} {4}} ca. 0,0667.}

und existiert somit durch algebraische Erweiterung der rationalen Zahlen.

Drehen und drehen[edit]

Dieser Abschnitt ist leer. Sie können helfen, indem Sie es hinzufügen. ((Dezember 2015)

Twist[edit]

Dieser Abschnitt ist leer. Sie können helfen, indem Sie es hinzufügen. ((Dezember 2015)

Polynome verbreiten[edit]

Wie für Doppel- und Dreifach-Spreads zu sehen ist, ist ein $n$ das Vielfache einer Ausbreitung, $s$ gibt ein Polynom in dieser Ausbreitung, bezeichnet $S. n ((s)$ als eine Lösung für die Triple-Spread-Formel.

In der herkömmlichen Sprache der Kreisfunktionen sind diese $n$ th-grad Polynome verbreiten, zum $n = 0, 1, 2, \dots$ kann durch die Identität charakterisiert werden:^{[citation needed]}

{ displaystyle sin ^ {2} (n theta) = S_ {n} left ( sin ^ {2} theta right).}

Identitäten[edit]

Explizite Formeln[edit]

${ displaystyle S_ {n} (s) = s sum _ {k = 0} ^ {n-1} { frac {n} {nk}} { binom {2n-1-k} {k}} (-4s) ^ {n-1-k}.}$
${ displaystyle S_ {n} (s) = { tfrac {1} {2}} – { tfrac {1} {4}} left (1-2s + 2 { sqrt {s ^ {2} – s}} right) ^ {n} – { tfrac {1} {4}} left (1-2s-2 { sqrt {s ^ {2} -s}} right) ^ {n}. }}$
${ displaystyle S_ {n} (s) = – { tfrac {1} {4}} left ( left ({ sqrt {1-s}} + i { sqrt {s}} right) ^ {2n} -1 rechts) ^ {2} links ({ sqrt {1-s}} – i { sqrt {s}} rechts) ^ {2n}.}$

Aus der Definition folgt unmittelbar daraus

{ displaystyle S_ {n} (s) = sin ^ {2} left (n arcsin left ({ sqrt {s}} right) right).}

Rekursionsformel[edit]

Die Triple-Spread-Formel

{ displaystyle (s_ {1} + s_ {2} + s_ {3}) ^ {2} = 2 left (s_ {1} ^ {2} + s_ {2} ^ {2} + s_ {3} ^ {2} right) + 4s_ {1} s_ {2} s_ {3}}

${ displaystyle (s_ {1} + s_ {2} + s_ {3}) ^ {2} = 2 left (s_ {1} ^ {2} + s_ {2} ^ {2} + s_ {3} ^ {2} right) + 4s_ {1} s_ {2} s_ {3}}$

ist eine Identität, deren Einträge selbst Polynome der Form sein können:

{ displaystyle s}

$s$ ,

{ displaystyle S_ {n} (s)}

${ displaystyle S_ {n} (s)}$ und

{ displaystyle S_ {n pm 1} (s)}

${ displaystyle S_ {n pm 1} (s)}$ ,

Nehmen Sie also einen Unterschied zu den Ausdrücken (und ordnen Sie sie neu an)

{ displaystyle (s + S_ {n} (s) + S_ {n + 1} (s)) ^ {2} = 2 left (s ^ {2} + S_ {n} (s) ^ {2} + S_ {n + 1} (s) ^ {2} right) + 4sS_ {n} (s) S_ {n + 1} (s)}

{ displaystyle (s + S_ {n} (s) + S_ {n-1} (s)) ^ {2} = 2 left (s ^ {2} + S_ {n} (s) ^ {2} + S_ {n-1} (s) ^ {2} right) + 4sS_ {n} (s) S_ {n-1} (s)}

ergibt die rekursiv Beziehung:

{ displaystyle S_ {n + 1} (s) = 2 (1-2s) S_ {n} (s) -S_ {n-1} (s) + 2s.}

Beziehung zu Chebyshev-Polynomen[edit]

Die Ausbreitungspolynome sind mit den Chebyshev-Polynomen der ersten Art verwandt, $T. n$ durch die Identität

{ displaystyle 1-2S_ {n} (s) = T_ {n} (1-2s).}

Dies impliziert^[1]

{ displaystyle S_ {n} (s) = { frac {1-T_ {n} (1-2s)} {2}} = 1-T_ {n} ^ {2} left ({ sqrt {1 -s}} right).}

Die zweite Gleichheit oben ergibt sich aus der Identität

{ displaystyle 2T_ {n} ^ {2} (x) -1 = T_ {2n} (x)}

auf Chebyshev-Polynomen.^{[citation needed]}

Komposition[edit]

Die Ausbreitungspolynome erfüllen die Zusammensetzungsidentität^[1]

{ displaystyle S_ {n} { bigl (} S_ {m} (s) { bigr)} = S_ {nm} (s).}

Koeffizienten in endlichen Feldern[edit]

Wenn angenommen wird, dass die Koeffizienten Mitglieder des endlichen Feldes sind $F. p$ , dann die Reihenfolge ${S. n}} n = 0, 1, 2, \dots$ der Ausbreitungspolynome ist periodisch mit der Periode $p 2 - 1 /. 2$ . Mit anderen Worten, wenn $k = p 2 - 1 /. 2$ , dann $S. n + k = S. n$ , für alle $n$ .^{[citation needed]}

Orthogonalität[edit]

Wenn die Koeffizienten als real angenommen werden, dann für $n \neq m$ , wir haben^[1]

{ displaystyle int _ {0} ^ {1} left (S_ {n} (s) – { tfrac {1} {2}} right) left (S_ {m} (s) – { tfrac {1} {2}} right) { frac {ds} { sqrt {s (1-s)}}} = 0.}

Zum $n = m$ ist das Integral $π$ /.8 es sei denn $n = m = 0$ In diesem Fall ist es $π$ /.4.^{[citation needed]}

Funktionen generieren[edit]

Die gewöhnliche Erzeugungsfunktion ist

{ displaystyle sum _ {n = 1} ^ { infty} S_ {n} (s) x ^ {n} = { frac {sx (1 + x)} {(1-x) ^ {3} + 4sx (1-x)}}.}

Die exponentielle Erzeugungsfunktion ist

{ displaystyle sum _ {n = 1} ^ { infty} { frac {S_ {n} (s)} {n!}} x ^ {n} = { tfrac {1} {2}} e ^ {x} left (1-e ^ {- 2sx} cos left (2x { sqrt {s (1-s)}} right) right).}

Differentialgleichung[edit]

$S. n ((s)$ erfüllt die lineare inhomogene Differentialgleichung zweiter Ordnung^{[citation needed]}

{ displaystyle s (1-s) y ” + left ({ tfrac {1} {2}} – s right) y ‘+ n ^ {2} left (y – { tfrac {1} {2}} right) = 0.}

Verbreiten Sie den Satz der Periodizität[edit]

Für jede ganze Zahl $n$ und jede Primzahl $p$ gibt es eine natürliche Zahl $m$ so dass $S. n ((s)$ ist teilbar durch $p$ genau wann $m$ teilt $n$ . Diese Nummer $m$ ist ein Teiler von beiden $p - 1$ oder $p + 1$ . Der Beweis dieser zahlentheoretischen Eigenschaft wurde erstmals in einer Arbeit von Shuxiang Goh und NJ Wildberger gegeben.^[7] Dabei wird das projektive Analogon zum Quadranten in der endlichen projektiven Linie betrachtet $P. 1 ((F. p)$ .

Tabelle der Ausbreitungspolynome mit Faktorisierungen[edit]

Die ersten verschiedenen Spread-Polynome lauten wie folgt:

{ displaystyle { begin {align} S_ {0} (s) = {} & 0 \[10pt]S_ {1} (s) = {} & s \[10pt]S_ {2} (s) = {} & 4s-4s ^ {2} \ = {} & 4s (1-s) \[10pt]S_ {3} (s) = {} & 9s-24s ^ {2} + 16s ^ {3} \ = {} & s (3-4s) ^ {2} \[10pt]S_ {4} (s) = {} & 16s-80s ^ {2} + 128s ^ {3} -64s ^ {4} \ = {} & 16s (1-s) (1-2s) ^ {2} .[10pt]S_ {5} (s) = {} & 25s-200s ^ {2} + 560s ^ {3} -640s ^ {4} + 256s ^ {5} \ = {} & s left (5-20s + 16s ^ {2} right) ^ {2} \[10pt]S_ {6} (s) = {} & 36s-420s ^ {2} + 1792s ^ {3} -3456s ^ {4} + 3072s ^ {5} -1024s ^ {6} \ = {} & 4s (1- s) (1-4s) ^ {2} (3-4s) ^ {2} \[10pt]S_ {7} (s) = {} & 49s-784s ^ {2} + 4704s ^ {3} -13440s ^ {4} + 19712s ^ {5} -14336s ^ {6} + 4096s ^ {7} \ = {} & s left (7-56s + 112s ^ {2} -64s ^ {3} right) ^ {2} \[10pt]S_ {8} (s) = {} & 64s-1344s ^ {2} + 10752s ^ {3} -42240s ^ {4} + 90112s ^ {5} -106496s ^ {6} \ & {} + 65536s ^ { 7} -16384s ^ {8} \ = {} & 64s (s-1) (1-2s) ^ {2} left (1-8s + 8s ^ {2} right) ^ {2} \[10pt]S_ {9} (s) = {} & 81s-2160s ^ {2} + 22176s ^ {3} -114048s ^ {4} + 329472s ^ {5} -559104s ^ {6} \ & {} + 552960s ^ { 7} -294912s ^ {8} + 65536s ^ {9} \ = {} & s (-3 + 4s) ^ {2} left (-3 + 36s-96s ^ {2} + 64s ^ {3} rechts) ^ {2} \[10pt]S_ {10} (s) = {} & 100s-3300s ^ {2} + 42240s ^ {3} -274560s ^ {4} + 1025024s ^ {5} \ & {} – 2329600s ^ {6} + 3276800s ^ { 7} -2785280s ^ {8} + 1310720s ^ {9} -262144s ^ {10} \ = {} & 4s (1-s) left (5-20s + 16s ^ {2} right) ^ {2} left (1-12s + 16s ^ {2} right) ^ {2} \[10pt]S_ {11} (s) = {} & 121s-4840s ^ {2} + 75504s ^ {3} -604032s ^ {4} + 2818816s ^ {5} \ & {} – 8200192s ^ {6} + 15319040s ^ { 7} -18382848s ^ {8} + 13697024s ^ {9} -5767168s ^ {10} + 1048576s ^ {11} \ = {} & s left (11-220s + 1232s ^ {2} -2816s ^ {3} + 2816s ^ {4} -1024s ^ {5} right) ^ {2} end {align}}}

Gesetze der rationalen Trigonometrie[edit]

Wildberger gibt an, dass es in der rationalen Trigonometrie fünf Grundgesetze gibt. Er gibt auch an, dass diese Gesetze mithilfe von Mathematik auf High-School-Niveau überprüft werden können. Einige entsprechen den trigonometrischen Standardformeln, wobei die Variablen als Quadranz und Streuung ausgedrückt werden.^[6]

In den folgenden fünf Formeln haben wir ein Dreieck aus drei Punkten $EIN 1, EIN 2, EIN 3$ . Die Ausbreitungen der Winkel an diesen Punkten sind $s 1, s 2, s 3$ , und $Q. 1, Q. 2, Q. 3$ sind die Quadranzen der gegenüberliegenden Dreieckseiten $EIN 1, EIN 2, EIN 3$ , beziehungsweise. Wie in der klassischen Trigonometrie, wenn wir drei der sechs Elemente kennen $s 1, s 2, s 3$ , $Q. 1, Q. 2, Q. 3$ und diese drei sind nicht die drei $s$ Dann können wir die anderen drei berechnen.

Dreifache Quad-Formel[edit]

Die drei Punkte $EIN 1, EIN 2, EIN 3$ sind genau dann kollinear, wenn:

{ displaystyle (Q_ {1} + Q_ {2} + Q_ {3}) ^ {2} = 2 left (Q_ {1} ^ {2} + Q_ {2} ^ {2} + Q_ {3} ^ {2} right)}

wo $Q. 1, Q. 2, Q. 3$ repräsentieren die Quadranzen zwischen $EIN 1, EIN 2, EIN 3$ beziehungsweise. Es kann entweder durch analytische Geometrie (das bevorzugte Mittel innerhalb der rationalen Trigonometrie) bewiesen oder aus der Heronschen Formel abgeleitet werden, wobei die Bedingung für die Kollinearität verwendet wird, dass das durch die drei Punkte gebildete Dreieck eine Nullfläche hat.

Beweis (zum Ein- / Ausblenden rechts klicken)

Abbildung der im Beweis verwendeten Nomenklatur.

Die Linie $AB$ hat die allgemeine Form:

{ displaystyle axe + by + c = 0}

wo die (nicht eindeutigen) Parameter $ein, b, c$ kann in Form von Punktkoordinaten ausgedrückt werden $EIN$ und $B.$ wie:

{ displaystyle { begin {align} a & = A_ {y} -B_ {y} \ b & = B_ {x} -A_ {x} \ c & = A_ {x} B_ {y} -A_ {y} B_ {x} end {align}}}

so dass überall auf der Linie:

{ displaystyle left (A_ {y} -B_ {y} right) x + left (B_ {x} -A_ {x} right) y + left (A_ {x} B_ {y} -A_ {y } B_ {x} right) = 0.}

Die Linie kann aber auch durch zwei gleichzeitige Gleichungen in einem Parameter angegeben werden $t$ , wo $t = 0$ am Punkt $EIN$ und $t = 1$ am Punkt $B.$ ::

{ displaystyle { begin {align} x & = (B_ {x} -A_ {x}) t + A_ {x}, \ y & = (B_ {y} -A_ {y}) t + A_ {y} , end {align}}}

oder in Bezug auf die ursprünglichen Parameter:

{ displaystyle { begin {align} x & = bt + A_ {x}, \ y & = – at + A_ {y}. end {align}}}

Wenn der Punkt $C.$ ist kollinear mit Punkten $EIN$ und $B.$ gibt es einen Wert von $t$ (für bestimmte Punkte, die nicht gleich 0 oder 1 sind), nennen Sie es $λ$ , für die diese beiden Gleichungen gleichzeitig an den Koordinaten des Punktes erfüllt sind $C.$ , so dass:

{ displaystyle { begin {align} C_ {x} & = b lambda + A_ {x}. \ C_ {y} & = – a lambda + A_ {y}. end {align}}}

Die Quadranzen der drei Liniensegmente sind nun durch die quadratischen Differenzen ihrer Koordinaten gegeben, die ausgedrückt werden können als $λ$ ::

{ displaystyle { begin {align} Q (AB) & equiv (B_ {x} -A_ {x}) ^ {2} + (B_ {y} -A_ {y}) ^ {2} \ & = b ^ {2} + (- a) ^ {2} \ & = a ^ {2} + b ^ {2} \[10pt]Q (BC) & equiv (C_ {x} -B_ {x}) ^ {2} + (C_ {y} -B_ {y}) ^ {2} \ & = { bigl (} (b Lambda + A_ {x}) – B_ {x} { bigr)} ^ {2} + { bigl (} (- a Lambda + A_ {y}) – B_ {y} { bigr)} ^ { 2} \ & = { bigl (} b lambda + (A_ {x} -B_ {x}) { bigr)} ^ {2} + { bigl (} -a lambda + (A_ {y } -B_ {y}) { bigr)} ^ {2} \ & = { bigl (} b lambda + (- b) { bigr)} ^ {2} + (- a lambda + a ) ^ {2} \ & = b ^ {2} ( lambda -1) ^ {2} + a ^ {2} (- lambda +1) ^ {2} \ & = b ^ {2} ( lambda -1) ^ {2} + a ^ {2} ( lambda -1) ^ {2} \ & = left (a ^ {2} + b ^ {2} right) ( lambda -1) ^ {2} \[10pt]Q (AC) & equiv (C_ {x} -A_ {x}) ^ {2} + (C_ {y} -A_ {y}) ^ {2} \ & = { bigl (} (b Lambda + A_ {x}) – A_ {x} { bigr)} ^ {2} + { bigl (} (- a Lambda + A_ {y}) – A_ {y} { bigr)} ^ { 2} \ & = (b lambda + A_ {x} -A_ {x}) ^ {2} + (- a lambda + A_ {y} -A_ {y}) ^ {2} \ & = (b lambda) ^ {2} + (- a lambda) ^ {2} \ & = b ^ {2} lambda ^ {2} + (- a) ^ {2} lambda ^ {2} \ & = b ^ {2} lambda ^ {2} + a ^ {2} lambda ^ {2} \ & = left (a ^ {2} + b ^ {2} right) lambda ^ {2} end {align}}}

wo die Tatsache genutzt wurde, dass $(- λ + 1) 2 = (λ - 1) 2$ .

Einsetzen dieser Quadranzen in die zu beweisende Gleichung:

{ displaystyle { begin {align} { bigl (} Q (AB) + Q (BC) + Q (AC) { bigr)} ^ {2} & = 2 left (Q (AB) ^ {2 } + Q (BC) ^ {2} + Q (AC) ^ {2} rechts) \ links ( links (a ^ {2} + b ^ {2} rechts) + links (a ^ {2} + b ^ {2} rechts) ( lambda -1) ^ {2} + links (a ^ {2} + b ^ {2} rechts) lambda ^ {2} rechts) ^ {2} & = 2 left ( left (a ^ {2} + b ^ {2} right) ^ {2} + left ( left (a ^ {2} + b ^ {2} right) ) ( lambda -1) ^ {2} rechts) ^ {2} + links ( links (a ^ {2} + b ^ {2} rechts) lambda ^ {2} rechts) ^ { 2} rechts) \ links (a ^ {2} + b ^ {2} rechts) ^ {2} links (1 + ( lambda -1) ^ {2} + lambda ^ {2} rechts) ^ {2} & = 2 links (a ^ {2} + b ^ {2} rechts) ^ {2} links (1+ links (( lambda -1) ^ {2} rechts) ^ {2} + left ( lambda ^ {2} right) ^ {2} right) end {align}}}

Nun, wenn $EIN$ und $B.$ verschiedene Punkte darstellen, so dass $ein 2 + b 2 \neq 0$ können wir beide Seiten durch teilen $Q. ((AB) 2 = (ein 2 + b 2) 2$ ::

{ displaystyle { begin {align} left (1+ lambda ^ {2} -2 lambda +1+ lambda ^ {2} right) ^ {2} & = 2 left (1+ left ( lambda ^ {2} -2 lambda +1 rechts) ^ {2} + lambda ^ {4} rechts) \ links (2 lambda ^ {2} -2 lambda +2 rechts ) ^ {2} & = 2 left (1+ lambda ^ {4} -2 lambda ^ {3} + lambda ^ {2} -2 lambda ^ {3} +4 lambda ^ {2} -2 lambda + lambda ^ {2} -2 lambda +1+ lambda ^ {4} rechts) \ 4 links ( lambda ^ {2} – lambda +1 rechts) ^ {2 } & = 2 left (2 lambda ^ {4} -4 lambda ^ {3} +6 lambda ^ {2} -4 lambda +2 right) \ 4 left ( lambda ^ {4 } – lambda ^ {3} + lambda ^ {2} – lambda ^ {3} + lambda ^ {2} – lambda + lambda ^ {2} – lambda +1 rechts) & = 4 left ( lambda ^ {4} -2 lambda ^ {3} +3 lambda ^ {2} -2 lambda +1 right) \ lambda ^ {4} -2 lambda ^ {3} +3 lambda ^ {2} -2 lambda +1 & = lambda ^ {4} -2 lambda ^ {3} +3 lambda ^ {2} -2 lambda +1 end {align}}}

Satz von Pythagoras[edit]

Die Linien $EIN 1 EIN 3$ (von Quadrance $Q. 1$ ) und $EIN 2 EIN 3$ (von Quadrance $Q. 2$ ) sind genau dann senkrecht (ihre Ausbreitung ist 1), wenn:

{ displaystyle Q_ {1} + Q_ {2} = Q_ {3}.}

wo $Q. 3$ ist der Quadrant zwischen $EIN 1$ und $EIN 2$ .

Dies entspricht dem Satz von Pythagoras (und seiner Umkehrung).

Es gibt viele klassische Beweise für den Satz von Pythagoras; Dieser ist in Bezug auf die rationale Trigonometrie gerahmt.

Das Ausbreitung eines Winkels ist das Quadrat seines Sinus. Angesichts des Dreiecks $△ ABC$ mit einem Abstand von 1 zwischen den Seiten $AB$ und $AC$ ,

{ Anzeigestil Q (AB) + Q (AC) = Q (BC)}

wo $Q.$ ist das “Quadrat”, dh das Quadrat der Entfernung.

Beweis

Abbildung der im Beweis verwendeten Nomenklatur.

Konstruiere eine Linie $ANZEIGE$ Teilen Sie den Spread von 1 mit dem Punkt $D.$ online $BC$ und einen Spread von 1 mit machen $DB$ und $DC$ . Die Dreiecke $△ ABC$ , $△ DBA$ und $△ DAC$ sind ähnlich (haben die gleichen Spreads, aber nicht die gleichen Quadranzen).

Dies führt zu zwei Gleichungen in Verhältnissen, die auf den Ausbreitungen der Seiten des Dreiecks basieren:

{ displaystyle { begin {align} s_ {C} & = { frac {Q (AB)} {Q (BC)}} && = { frac {Q (BD)} {Q (AB)}} && = { frac {Q (AD)} {Q (AC)}}. \ s_ {B} & = { frac {Q (AC)} {Q (BC)}} && = { frac {Q ( DC)} {Q (AC)}} && = { frac {Q (AD)} {Q (AB)}}. End {align}}}

Im Allgemeinen ergeben sich die beiden Spreads aus der Aufteilung eines Spreads in zwei Teile als Linie $ANZEIGE$ tut für die Verbreitung $TAXI$ , addieren Sie nicht zum ursprünglichen Spread, da der Spread eine nichtlineare Funktion ist. Wir beweisen also zunächst, dass das Teilen eines Spread von 1 zu zwei Spreads führt, die sich zum ursprünglichen Spread von 1 addieren.

Der Einfachheit halber, aber ohne Verlust der Allgemeinheit, richten wir die Linien, die sich mit einer Streuung von 1 schneiden, auf die Koordinatenachsen aus und beschriften die Trennlinie mit Koordinaten $((x 1, y 1)$ und $((x 2, y 2)$ . Dann sind die beiden Spreads gegeben durch:

{ displaystyle { begin {align} s_ {1} & = { frac {(x_ {2} -x_ {2}) ^ {2} + (y_ {2} -y_ {1}) ^ {2} } {(x_ {2} -x_ {1}) ^ {2} + (y_ {2} -y_ {1}) ^ {2}} && = { frac {(y_ {2} -y_ {1 }) ^ {2}} {(x_ {2} -x_ {1}) ^ {2} + (y_ {2} -y_ {1}) ^ {2}}}, \ s_ {2} & = { frac {(x_ {2} -x_ {1}) ^ {2} + (y_ {2} -y_ {2}) ^ {2}} {(x_ {2} -x_ {1}) ^ { 2} + (y_ {2} -y_ {1}) ^ {2}}} && = { frac {(x_ {2} -x_ {1}) ^ {2}} {(x_ {2} -x_ {1}) ^ {2} + (y_ {2} -y_ {1}) ^ {2}}}. End {align}}}

Daher

{ displaystyle s_ {1} + s_ {2} = { frac {(x_ {2} -x_ {1}) ^ {2} + (y_ {2} -y_ {1}) ^ {2}} { (x_ {2} -x_ {1}) ^ {2} + (y_ {2} -y_ {1}) ^ {2}}} = 1,}

damit

{ displaystyle s_ {C} + s_ {B} = 1.}

Unter Verwendung der ersten beiden Verhältnisse aus dem ersten Satz von Gleichungen kann dies umgeschrieben werden:

{ displaystyle { frac {Q (AB)} {Q (BC)}} + { frac {Q (AC)} {Q (BC)}} = 1.}

Multiplizieren Sie beide Seiten mit $Q. ((BC)$ ::

{ Anzeigestil Q (AB) + Q (AC) = Q (BC).}

QED

Gesetz verbreiten[edit]

Für jedes Dreieck $△ EIN 1 EIN 2 EIN 3$ mit Quadranzen ungleich Null:^[1]

{ displaystyle { frac {s_ {1}} {Q_ {1}}} = { frac {s_ {2}} {Q_ {2}}} = { frac {s_ {3}} {Q_ {3 }}}.}

Dies ist das Gesetz der Sinus, nur im Quadrat.

Cross Law[edit]

Für jedes Dreieck $△ EIN 1 EIN 2 EIN 3$ ,^[1]

{ displaystyle (Q_ {1} + Q_ {2} -Q_ {3}) ^ {2} = 4Q_ {1} Q_ {2} (1-s_ {3}).}

Dies ist analog zum Kosinusgesetz. Es wird das “Kreuzgesetz” genannt, weil $(1 - s 3)$ Das Quadrat des Kosinus des Winkels wird als “Kreuz” bezeichnet.

Triple-Spread-Formel[edit]

Für jedes Dreieck $△ EIN 1 EIN 2 EIN 3$ ,^[1]

{ displaystyle (s_ {1} + s_ {2} + s_ {3}) ^ {2} = 2 left (s_ {1} ^ {2} + s_ {2} ^ {2} + s_ {3} ^ {2} right) + 4s_ {1} s_ {2} s_ {3}.}

Diese Beziehung kann aus der Formel für den Sinus eines zusammengesetzten Winkels abgeleitet werden: In einem Dreieck (dessen drei Winkel sich zu 180 ° summieren) haben wir,

{ displaystyle sin (a) = sin (b + c) = sin (b) cos (c) + sin (c) cos (b)}

Entsprechend beschreibt es die Beziehung zwischen den Ausbreitungen von drei gleichzeitigen Linien, da die Ausbreitung (wie der Winkel) nicht beeinflusst wird, wenn die Seiten eines Dreiecks parallel zu sich selbst bewegt werden, um sich an einem gemeinsamen Punkt zu treffen.

Wenn Sie zwei Spreads kennen, kann der dritte durch Lösen der zugehörigen quadratischen Formel berechnet werden. Da zwei Lösungen hergestellt werden, weiter Dreiecksverbreitungsregeln muss verwendet werden, um die entsprechende auszuwählen. Während dies komplexer erscheint als das Erhalten eines zusätzlichen Winkels direkt durch Subtraktion, ist der irrationale Wert von ‘ $π$ ‘(implizit in der Winkelsumme eines Dreiecks vorhanden) wird vermieden.

Trigonometrie über beliebige Felder[edit]

Da die Gesetze der rationalen Trigonometrie algebraische (und nicht transzendentale) Beziehungen ergeben, gelten sie allgemein für algebraische Zahlenfelder jenseits der rationalen Zahlen. Insbesondere reproduziert jedes endliche Feld, das keine Charakteristik 2 hat, eine Form dieser Gesetze und damit eine endliche Feldgeometrie.^[8] Die ‘Ebene’, die durch ein endliches Feld gebildet wird $F. p$ ist das kartesische Produkt $F. p \times F. p$ aller geordneten Paare von Feldelementen, wobei gegenüberliegende Kanten identifiziert wurden, die die Oberfläche bilden, die topologisch einem diskretisierten Torus entspricht. Einzelne Elemente entsprechen Standardpunkten und Linien für Sätze von nicht mehr als

{ displaystyle p}

$p$ Punkte, die durch Inzidenz (einen Anfangspunkt) plus Richtung oder Steigung in niedrigsten Begriffen (sagen Sie alle Punkte ‘2 über und 1 nach oben’) angegeben sind und die Ebene vor dem Wiederholen ‘umwickeln’.

Beispiel: (Überprüfen Sie das Verbreitungsgesetz in $F. 13$ )[edit]

Die Abbildung (rechts) zeigt a Dreieck von drei solchen Linien in der Finite-Felder-Einstellung $F. 13 \times F. 13$ ::

Jede Linie hat ein eigenes Symbol und die Schnittpunkte von Linien (Eckpunkte) ist gekennzeichnet durch zwei Symbole an Punkten vorhanden:

Ein Dreieck durch die Punkte

(2, 8)

(9, 9)

, und

(100)

der endlichen Feldebene

F. 13 \times F. 13

(2, 8), (9, 9) und (10, 0).

Verwenden von Satz von Pythagoras Mit dem arithmetischen Modulo 13 finden wir, dass diese Seiten Quadranzen haben von:

(9 – 2)² + (9 – 8)² = 50 ≤ 11 mod 13

(9 – 10)² + (9 – 0)² = 82 ≤ 4 mod 13

(10 – 2)² + (0 – 8)² = 128 ≤ 11 mod 13

Neuordnung des Kreuzgesetzes als

{ displaystyle s_ {3} = 1 – { frac {(Q_ {1} + Q_ {2} -Q_ {3}) ^ {2}} {4Q_ {1} Q_ {2}}}

gibt separate Ausdrücke für jeden Spread in Bezug auf die drei Quadranzen an:

1 – ((4 + 11 – 11)²4 × 4 × 11 = 1 – 37 ≡ 8 mod 13

1 – ((11 + 11 – 4)²4 × 11 × 11 = 1 – 123 ≡ 10 mod 13

1 – ((4 + 11 – 11)²4 × 4 × 11 = 1 – 37 ≡ 8 mod 13

Wir stellen wiederum fest, dass diese Verhältnisse alle gleich sind – gemäß dem Spread-Gesetz (zumindest in Mod 13):

811 :: 104 :: 811

Da das erste und das letzte Verhältnis übereinstimmen (das Dreieck bilden gleichschenklig) Wir kreuzen uns einfach und nehmen Unterschiede, um auch die Gleichheit mit dem mittleren Verhältnis zu zeigen:

11 × 10 – 8 × 4 = 78 ≤ 0 mod 13

Andernfalls wird angenommen, dass die euklidische Standardebene nur aus rationalen Punkten besteht. $ℚ \times ℚ$ , wobei nichtalgebraische Zahlen als Lösungen weggelassen werden. Eigenschaften wie das Auftreten von Objekten, die die Lösungen oder den ‘Inhalt’ von geometrischen Theoremen darstellen, folgen daher einem zahlentheoretischen Ansatz, der sich unterscheidet und restriktiver ist als einer, der reelle Zahlen zulässt. Zum Beispiel, nicht alle Es wird angenommen, dass Linien, die durch den Mittelpunkt eines Kreises verlaufen, den Kreis an seinem Umfang treffen. Um einfallend zu sein, müssen solche Linien die Form haben

{ displaystyle { begin {align} ax + by & = 0 \ a ^ {2} + b ^ {2} & = c ^ {2} end {align}} quad a, b, c in mathbb {Q}}

und unbedingt den Kreis in a treffen rational Punkt.

Berechnung – Komplexität und Effizienz[edit]

Die rationale Trigonometrie macht fast alle Probleme nur mit Addition, Subtraktion, Multiplikation oder Division lösbar, da trigonometrische Funktionen (des Winkels) zugunsten trigonometrischer Verhältnisse in quadratischer Form gezielt vermieden werden.^[6] Daher können die als Abstand (oder Winkel) erforderlichen Ergebnisse höchstens aus einem genau bewerteten rationalen Äquivalent der Quadranz (oder Streuung) angenähert werden, nachdem diese einfacheren Operationen ausgeführt wurden. Um diesen Vorteil nutzen zu können, muss jedes Problem entweder in Bezug auf vorherige Quadranzen und Spreads angegeben oder eingerichtet werden, was zusätzliche Arbeit erfordert.^[9]

Die Gesetze der rationalen Trigonometrie, die algebraisch sind, führen Feinheiten in die Lösung von Problemen ein, wie z. geschätzte Ergebnisse. Im Gegensatz dazu wird im klassischen Fach Linearität in Entfernungs- und Winkelmessungen einbezogen, um diese Operationen zu vereinfachen, wenn auch durch “transzendentale” Techniken, bei denen reelle Zahlen verwendet werden, die eine ungefähre Wertausgabe beinhalten.

Siehe auch[edit]

^ Wildbergers Ansichten zur Geschichte der Unendlichkeit finden Sie im Artikel von Gefter New Scientist, aber auch in Wildbergers Vorlesungen zur Geschichte der Mathematik und zu den Grundlagen der Mathematik, Universität von New South Wales, circa 2009–2014, in mehr als 120 Videos und Vorlesungen, die online unter @youtube verfügbar sind
^ Sehen Göttliche Proportionen für zahlreiche Beispiele für Berechnungen mit rationalen trigonometrischen Funktionen sowie für Probleme bei der Anwendung der rationalen Trigonometrie auf Situationen, die irrationale Werte enthalten.

Verweise[edit]

^ ^ein ^b ^c ^d ^e ^f ^G ^h ^ich ^j Wildberger, Norman John (2005). Göttliche Proportionen: Rationale Trigonometrie zur universellen Geometrie (1. Aufl.). Australien: Wild Egg Pty Ltd. ISBN 0-9757492-0-X. Abgerufen 2015-12-01.
^ ^ein ^b ^c “”Das Ende der Unendlichkeit: Zeit, die unendliche Geschichte hinter sich zu lassen?“von Amanda Gefter, New Scientist, 15. August 2013
^ http://www.maa.org/publications/maa-reviews/divine-proportions-rational-trigonometry-to-universal-geometry
^ J. Franklin, Überprüfung von Göttliche Proportionen, Mathematischer Intelligencer 28 (3) (2006), 73-4.
^ http://web.maths.unsw.edu.au/~norman/papers/TrigComparison.pdf
^ ^ein ^b ^c ^d ^e ^f Wildberger, Norman J. (2007). “Ein rationaler Ansatz zur Trigonometrie”. Mathe-Horizonte. Washington, DC: Mathematische Vereinigung von Amerika. November 2007: 16–20. ISSN 1072-4117.
^ Shuxiang Goh, NJ Wildberger (5. November 2009). “Verbreiten Sie Polynome, Rotationen und den Schmetterlingseffekt”. arXiv:0911.1025. Bibcode:2009arXiv0911.1025G.
^ Le Anh Vinh, Dang Phuong Dung (17. Juli 2008). “Explizite harte Ramsey-Graphen”. arXiv:0807.2692. Bibcode:2008arXiv0807.2692V. , Seite 1. Eine andere Version dieses Artikels ist bei Le Anh Vinh, Dang Phuong Dung (2008), “Explizite harte Ramsey-Graphen Archiviert 2012-10-11 an der Wayback Machine “, Tagungsband der Internationalen Konferenz über Beziehungen, Ordnungen und Grafiken: Interaktion mit der Informatik 2008, Nouha Editions, 139–146.
^ Olga Kosheleva (2008), “Rationale Trigonometrie: rechnerischer Standpunkt“, Geombinatorics, Vol. 1, No. 1, S. 18–25.

Allgemeine Referenzen[edit]

Externe Links[edit]

after-content-x4