Null-unterdrücktes Entscheidungsdiagramm – Wikipedia

EIN Null-unterdrücktes Entscheidungsdiagramm ((ZSDD oder ZDD) ist eine bestimmte Art von binärem Entscheidungsdiagramm (BDD) mit fester variabler Reihenfolge. Diese Datenstruktur bietet eine kanonisch kompakte Darstellung von Mengen, die insbesondere für bestimmte kombinatorische Probleme geeignet ist. Erinnern Sie sich an die OBDD-Reduktionsstrategie, dh ein Knoten wird aus dem Entscheidungsbaum entfernt, wenn beide Außenkanten auf denselben Knoten zeigen. Im Gegensatz dazu wird ein Knoten in einem ZDD entfernt, wenn seine positive Kante auf den Endknoten 0 zeigt. Dies bietet eine alternative starke Normalform mit verbesserter Komprimierung von dünn besetzten Sätzen. Es basiert auf einer Reduktionsregel von Shin-ichi Minato im Jahr 1993.

Hintergrund[edit]

In einem binären Entscheidungsdiagramm kann eine boolesche Funktion als verwurzelter, gerichteter azyklischer Graph dargestellt werden, der aus mehreren Entscheidungsknoten und Endknoten besteht. 1993 modifizierte Shin-ichi Minato aus Japan Randal Bryants BDDs zur Lösung kombinatorischer Probleme. Seine “Zero-Suppressed” BDDs zielen darauf ab, spärliche Sätze von Bitvektoren darzustellen und zu manipulieren. Wenn die Daten für ein Problem als Bitvektoren der Länge n dargestellt werden, kann jede Teilmenge der Vektoren durch die Boolesche Funktion über n Variablen dargestellt werden, was 1 ergibt, wenn sich der der Variablenzuweisung entsprechende Vektor in der Menge befindet.

Laut Bryant ist es möglich, Formen von Logikfunktionen zu verwenden, um Probleme mit der Summe der Produkte auszudrücken. Solche Formen werden oft als Sätze von “Würfeln” dargestellt, die jeweils durch eine Zeichenfolge mit den Symbolen 0, 1 und – gekennzeichnet sind. Zum Beispiel die Funktion

${ displaystyle ({ bar {x}} _ {1} land x_ {2}) lor ({ bar {x}} _ {2} bigoplus x_ {3})}$

kann durch das Set veranschaulicht werden

${ displaystyle {01 -, – 11, -00 }}$

. Durch Verwendung der Bits 10, 01 und 00 zur Bezeichnung der Symbole 1, 0 bzw. – kann der obige Satz mit Bitvektoren in Form von dargestellt werden

${ displaystyle {011000,001010,000101 }}$

. Beachten Sie, dass der Satz von Bitvektoren dünn ist, da die Anzahl der Vektoren weniger als 2 beträgtⁿDies ist die maximale Anzahl von Bitvektoren, und die Menge enthält viele Elemente gleich Null. In diesem Fall kann ein Knoten weggelassen werden, wenn das Setzen der Knotenvariablen auf 1 bewirkt, dass die Funktion 0 ergibt. Dies wird unter der Bedingung gesehen, dass eine 1 an einer Bitposition impliziert, dass der Vektor nicht in der Menge ist. Bei spärlichen Mengen ist diese Bedingung häufig, und daher sind viele Knoteneliminierungen möglich.

Minato hat bewiesen, dass ZDDs besonders für kombinatorische Probleme geeignet sind, wie die klassischen Probleme in zweistufige Logikminimierung, Ritter-Tour-Problem, Fehlersimulation, Timing-Analyse, das N-Königinnen-Problem sowie schwache Teilung. Durch die Verwendung von ZDDs kann die Größe der Darstellung eines Satzes von n-Bit-Vektoren in OBDDs um höchstens einen Faktor von n reduziert werden. In der Praxis ist die Optimierung statistisch signifikant.

Definitionen[edit]

Wir definieren ein Zero-Suppressed Decision Diagram (ZDD) als einen gerichteten azyklischen Graphen, so dass:

1. Ein Endknoten ist entweder:

• Der spezielle ⊤-Knoten (der TRUE-Knoten) oder:
• Der spezielle ⊥-Knoten (der FALSE-Knoten).

2. Jeder nicht terminale Knoten erfüllt die folgenden Bedingungen:

ein. Der Knoten ist mit einer positiven Ganzzahl v gekennzeichnet. Diese Bezeichnung muss nicht eindeutig sein.

b. Der Knoten hat einen Out-Grad von 2. Eine der ausgehenden Kanten heißt “LO” und die andere “HI”. (In Diagrammen kann man gepunktete Linien für LO-Kanten und durchgezogene Linien für HI-Kanten zeichnen.)

c. Ein Zielknoten ist entweder terminal oder mit einer Ganzzahl gekennzeichnet, die streng größer als v ist. Daher kann man Pfeilspitzen in Diagrammen weglassen, da die Kantenrichtungen aus den Beschriftungen abgeleitet werden können.

d. Die HI-Kante zeigt niemals auf den ⊥-Knoten.

3. Es gibt genau einen Knoten mit einem Grad von Null – den Wurzelknoten. Der Wurzelknoten ist entweder terminal oder durch die kleinste Ganzzahl im Diagramm gekennzeichnet.

4. Wenn zwei Knoten dieselbe Bezeichnung haben, zeigen ihre LO- oder HI-Kanten auf unterschiedliche Knoten. Mit anderen Worten, es gibt keine redundanten Knoten.

Wir nennen Z eine nicht reduzierte ZDD, wenn eine HI-Kante auf einen ⊥-Knoten zeigt oder Bedingung 4 nicht gilt.

In Computerprogrammen können Boolesche Funktionen in Bits ausgedrückt werden, sodass der ⊤-Knoten und der ⊥-Knoten durch 1 und 0 dargestellt werden können. Aus der obigen Definition können wir Kombinationssätze effizient darstellen, indem wir zwei Regeln auf die BDDs anwenden:

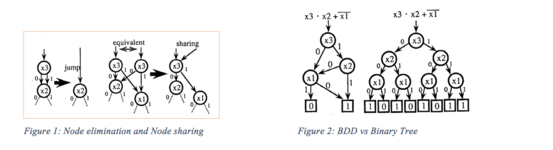
1.Entfernen Sie alle Knoten, deren 1-Kante auf den 0-Terminal-Knoten zeigt. Verbinden Sie dann die Kante direkt mit dem anderen Teilgraphen, wie in Abbildung 1 dargestellt.

2. Teilen Sie alle äquivalenten Untergraphen wie bei Original-BDDs.

Wenn die Anzahl und die Reihenfolge der Eingabevariablen festgelegt sind, stellt eine Null-unterdrückte BDD eine Boolesche Funktion eindeutig dar (wie in Abbildung 2 gezeigt, kann eine BDD zur Darstellung eines Booleschen Binärbaums verwendet werden).

Darstellung einer Familie von Sets[edit]

Sei F ein ZDD. Sei v sein Wurzelknoten. Dann:

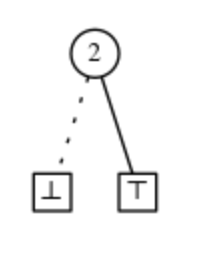
1. Wenn v = ⊥, kann es keine anderen Knoten geben, und F steht für Ø, die leere Familie.

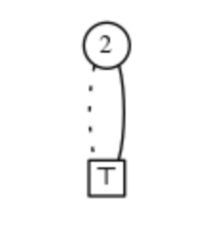
2. Wenn v = ⊤, kann es keine anderen Knoten geben, und F steht für die Familie, die nur die leere Menge {Ø} enthält. Wir nennen dies eine Einheitsfamilie und bezeichnen sie mit.

3. Wenn v zwei Kinder hat. Sei v0 der LO-Knoten und v1 der HI-Knoten. Sei Fi die Familie, die durch das in vi verwurzelte ZDD repräsentiert wird, was durch einen Induktionsnachweis gezeigt werden kann. Dann repräsentiert F die Familie

${ displaystyle F_ {0} cup { alpha cup {v } mid alpha in F_ {1} }}$

Man kann den LO-Zweig als die Mengen in F darstellen, die nicht enthalten v::

${ displaystyle F_ {0} = { alpha: alpha in F, v notin alpha }}$

Und der HI-Zweig als die Mengen in F, die enthalten v::

${ displaystyle F_ {1} = { alpha backslash {v }: alpha in F, v in alpha }}$

Beispiel[edit]

Abbildung 3: Die Familie

${ displaystyle Emptyset Cup { Emptyset Cup {2 } } = { {2 } }}$

. Wir können das nennen

${ displaystyle e_ {2}}$

, eine elementare Familie. Grundfamilien bestehen aus der Form

${ displaystyle { {n } }}$

und werden mit bezeichnet

${ displaystyle e_ {n}}$

.

Abbildung 4: Die Familie

${ displaystyle { Emptyset } cup { Emptyset cup {2 } } = { leer, {2 } }}$

Abbildung 5: Die Familie

${ displaystyle { {2 } } cup { Emptyset cup {1 } } = { {1 }, {2 } }}$

Abbildung 6: Die Familie

${ displaystyle { {1 } cup {2 } } = { {1,2 } }}$

Eigenschaften[edit]

Ein Merkmal von ZDDs ist, dass das Formular nicht von der Anzahl der Eingabevariablen abhängt, solange die Kombinationssätze gleich sind. Es ist nicht erforderlich, die Anzahl der Eingabevariablen festzulegen, bevor Diagramme erstellt werden. ZDDs unterdrücken automatisch die Variablen für Objekte, die niemals in Kombination erscheinen, daher die Effizienz für die Bearbeitung spärlicher Kombinationen. Ein weiterer Vorteil von ZDDs besteht darin, dass die Anzahl der 1-Pfade im Diagramm genau der Anzahl der Elemente im Kombinationssatz entspricht. In ursprünglichen BDDs bricht die Knoteneliminierung diese Eigenschaft. Daher sind ZDDs besser als einfache BDDs, um Kombinationssätze darzustellen. Es ist jedoch besser, die ursprünglichen BDDs zu verwenden, wenn gewöhnliche Boolesche Funktionen dargestellt werden (siehe Abbildung 7).

Grundoperationen[edit]

Hier haben wir die grundlegenden Operationen für ZDDs, da sie sich geringfügig von denen der ursprünglichen BDDs unterscheiden. In Abbildung 8 sind Beispiele aufgeführt, die aus der folgenden Tabelle hervorgehen.

Empty () gibt ø zurück (leere Menge)

Base () gibt {0} zurück

Subset1 (P, var) gibt die Subset von P zurück, wie z var = 1

Subset0 (P, var) gibt die Subset von P zurück, wie z var = 0

Change (P, var) gibt P zurück, wenn var ist invertiert

Union (P, Q) kehrt zurück (

${ displaystyle P cup Q}$

)

Intsec (P, Q) gibt zurück (

${ displaystyle P cap Q}$

)

Diff (P, Q) gibt zurück (

${ displaystyle PQ}$

)

Count (P) kehrt zurück

${ displaystyle left vert P right vert}$

. (Anzahl der Elemente)

In ZDDs gibt es keine NOT-Operation, was bei Original-BDDs eine wesentliche Operation ist. Der Grund ist, dass das Komplement gesetzt ist

${ displaystyle { bar {P}}}$

kann nicht berechnet werden, ohne die universelle Menge zu definieren

${ displaystyle U}$

. In ZDDs,

${ displaystyle { bar {P}}}$

kann als Diff (U, P) berechnet werden.

Algorithmen[edit]

Annehmen

${ displaystyle left vert P right vert = left vert P_ {0} right vert + left vert P_ {1} right vert}$

können wir die Anzahl der Sätze in einem ZDD rekursiv berechnen, wodurch wir den 34. Satz einer 54-köpfigen Familie erhalten. Der Direktzugriff ist schnell und jede Operation, die für ein Array von Sätzen möglich ist, kann mit einem ZDD effizient ausgeführt werden.

Laut Minato können die obigen Operationen für ZDDs wie ursprüngliche BDDs rekursiv ausgeführt werden. Um die Algorithmen einfach zu beschreiben, definieren wir die Prozedur Getnode(top, P0, P1) das gibt einen Knoten für eine Variable top und zwei Untergraphen P0 und P1 zurück. Wir können eine Hash-Tabelle namens uniq-table verwenden, um jeden Knoten eindeutig zu halten. Das Entfernen und Teilen von Knoten wird nur von verwaltet Getnode().

 Getnode (top, P0, P1) {
   if (P1 == ø) return P0; /* node elimination */
   P = search a node with (top, P0, P1 ) in uniq-table; if (P exist) return P; /* node sharing */
   P = generate a node with (top, P0, P1 );
   append P to the uniq-table;
   return P; 
 }

Verwenden von Getnode()können wir dann andere grundlegende Operationen wie folgt darstellen:

 Subset1 (P, var) {
   if (P.top < var) return ø; 
   if (P.top == var) return P1; 
   if (P.top > var)
     return Getnode (P.top, Subset1(P0, var), Subset1(P1, var));
 } 

 Subset0 (P, var) {
   if (P.top < var) return ø; 
   if (P.top == var) return P0; 
   if (P.top > var)
     return Getnode (P.top, Subset0(P0, var), Subset0(P1, var));
 } 

 Change (P, var) {
   if (P.top < var) return Getnode (var, ø, P); 
   if (P.top == var) return Getnode (var, P1, P0);
   if (P.top > var)
     return Getnode (P.top, Change(P0, var), Change(P1, var));
 }

 Union (P, Q) {
   if (P == ø) return Q; 
   if (Q == ø) return P;
   if (P == Q) return P;
   if (P.top > Q.top) return Getnode (P.top, Union(P0, Q), P1);
   if (P.top < Q.top) return Getnode (Q.top, Union(P, Q0), Q1);
   if (P.top == Q.top) 
     return Getnode (P.top, Union(P0, Q0), Union(P1, Q1));
 }

 Intsec (P, Q) {
   if (P == ø) return ø; 
   if (Q == ø) return ø;
   if (P == Q) return P;
   if (P.top > Q.top) return Intsec(P0, Q);
   if (P.top < Q.top) return Intsec (P, Q0);
   if (P.top == Q.top) 
     return Getnode (P.top, Intsec(P0, Q0), Intsec(P1, Q1));
 }

 Diff (P, Q) {
   if (P == ø) return ø; 
   if (Q == ø) return P;
   if (P == Q) return ø;
   if (P.top > Q.top) return Getnode(P.top, Diff(P0, Q), P1;)
   if (P.top < Q.top) return Diff(P, Q0);
   if (P.top == Q.top) 
     return Getnode (P.top, Diff(P0, Q0), Diff(P1, Q1));
 }

 Count (P) {
   if (P == ø) return 0; 
   if (P == {ø}) return 1;
     return Count(P0) + Count(P1);
 }

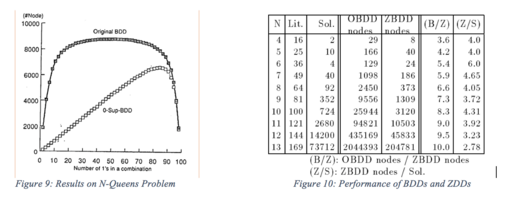
Diese Algorithmen benötigen im schlimmsten Fall eine exponentielle Zeit für die Anzahl der Variablen. Wir können jedoch die Leistung verbessern, indem wir einen Cache verwenden, der die Ergebnisse der letzten Vorgänge in BDDs auf ähnliche Weise speichert. Der Cache verhindert doppelte Ausführungen für äquivalente Subgraphen. Ohne Duplikate können die Algorithmen in einer Zeit arbeiten, die proportional zur Größe der Diagramme ist (siehe Abbildung 9 und 10).

Anwendung[edit]

ZDDs als Wörterbücher[edit]

ZDDs können verwendet werden, um die Wörter mit fünf Buchstaben des Englischen darzustellen, die Menge WORDS (Größe 5757) aus dem Stanford GraphBase zum Beispiel. Eine Möglichkeit, dies zu tun, besteht darin, die Funktion zu berücksichtigen

${ displaystyle f (x_ {1}, ..., x_ {25})}$

das ist genau dann als 1 definiert, wenn die fünf Zahlen

${ displaystyle (x_ {1}, ..., x_ {5}) _ {2}}$

,

${ displaystyle (x_ {6}, ..., x_ {10}) _ {2}}$

, ...,

${ displaystyle (x_ {21}, ..., x_ {25}) _ {2}}$

codieren Sie die Buchstaben eines englischen Wortes, wobei

${ displaystyle a = (00001) _ {2}}$

, ...,

${ displaystyle z = (11010) _ {2}}$

. Zum Beispiel,

${ displaystyle f (0,0,1,1,1,0,1,1,1,1,1,1,1,1,1,0,0,1,1,0,1,1,0 , 0, x_ {25}) = x_ {25}}$

. Die Funktion von 25 Variablen hat Z (f) = 6233 Knoten - was für die Darstellung von 5757 Wörtern nicht schlecht ist. Im Vergleich zu Binärbäumen, Versuchen oder Hash-Tabellen ist ein ZDD möglicherweise nicht das Beste, um einfache Suchvorgänge durchzuführen. Es ist jedoch effizient beim Abrufen von Daten, die nur teilweise angegeben sind, oder von Daten, die nur ungefähr einem Schlüssel entsprechen sollen. Komplexe Abfragen können problemlos bearbeitet werden. Darüber hinaus enthalten ZDDs nicht so viele Variablen. Tatsächlich kann man mit einem ZDD diese fünf Buchstaben als spärliche Funktion darstellen

${ displaystyle F (a_ {1}, ..., z_ {1}, a_ {2}, ..., z_ {2}, ..., a_ {5}, ..., z_ {5} )}$

das hat 26 × 5 = 130 Variablen, wobei Variable

${ displaystyle a_ {2}}$

Bestimmt beispielsweise, ob der zweite Buchstabe "a" ist. Um das Wort "verrückt" darzustellen, kann man F wahr machen, wenn

${ displaystyle c_ {1} = r_ {2} = a_ {3} = z_ {4} = y_ {5} = 1}$

und alle anderen Variablen sind 0. Somit kann F als eine Familie betrachtet werden, die aus den 5757 Teilmengen besteht

${ displaystyle {w_ {1}, h_ {2}, i_ {3}, c_ {4}, h_ {5} }}$

usw. Mit diesen 130 Variablen beträgt die ZDD-Größe Z (F) tatsächlich 5020 anstelle von 6233. Laut Knuth beträgt die äquivalente Größe von B (F) unter Verwendung eines BDD 46.189 - deutlich größer als Z (F). Trotz ähnlicher Theorien und Algorithmen übertreffen ZDDs BDDs für dieses Problem mit einem ziemlich großen Spielraum. Folglich können wir mit ZDDs bestimmte Abfragen ausführen, die für BDDs zu lästig sind. Komplexe Familien von Teilmengen können leicht aus Elementarfamilien konstruiert werden. Um nach Wörtern zu suchen, die ein bestimmtes Muster enthalten, kann man zur Berechnung die Familienalgebra auf ZDDs verwenden

${ displaystyle (F / P) sqcup P}$

wobei P das Muster ist, z

${ displaystyle a_ {1} sqcup h_ {3} sqcup e_ {5}}$

.

ZDDs zur Darstellung einfacher Pfade[edit]

Man kann ZDDs verwenden, um einfache Pfade in einem ungerichteten Graphen darzustellen. Zum Beispiel gibt es 12 Möglichkeiten, von der oberen linken Ecke eines Drei-mal-Drei-Gitters (siehe Abbildung 11) zur unteren rechten Ecke zu gelangen, ohne einen Punkt zweimal zu besuchen.

Diese Pfade können durch das in Abbildung 13 gezeigte ZDD dargestellt werden. In diesem ZDD erhalten wir den ersten Pfad, indem wir die HI-Zweige am Knoten 13, Knoten 36, Knoten 68 und Knoten 89 des ZDD nehmen (LO-Zweige, die einfach zu ⊥ gehen weggelassen werden). Obwohl der ZDD in Abbildung 13 keineswegs signifikant erscheint, werden die Vorteile eines ZDD offensichtlich, wenn das Gitter größer wird. Beispielsweise ergibt sich für ein Raster von acht mal acht die Anzahl der einfachen Pfade von Ecke zu Ecke zu 789, 360.053.252 (Knuth). Die Pfade können mit 33580 Knoten unter Verwendung eines ZDD dargestellt werden.

Randal Bryant schlug ein Beispiel aus der Praxis für einfache Wege vor: „Angenommen, ich wollte eine Fahrt durch die kontinentalen USA machen, alle Landeshauptstädte besuchen und nur einmal durch jeden Staat fahren. Welchen Weg sollte ich nehmen, um die Gesamtentfernung zu minimieren? “ Abbildung 14 zeigt ein ungerichtetes Diagramm für diese Roadmap, wobei die Zahlen die kürzesten Entfernungen zwischen benachbarten Hauptstädten angeben. Das Problem besteht darin, eine Teilmenge dieser Kanten auszuwählen, die einen Hamilton-Pfad mit der kleinsten Gesamtlänge bilden. Jeder Hamilton-Pfad in diesem Diagramm muss entweder in Augusta, Maine (ME) beginnen oder enden. Angenommen, man beginnt in CA. Man kann ein ZDD finden, das alle Pfade von CA nach ME charakterisiert. Laut Knuth hat dieses ZDD nur 7850 Knoten und zeigt effektiv, dass genau 437.525.772.584 einfache Pfade von CA nach ME möglich sind. Nach Anzahl der Kanten ist die Erzeugungsfunktion

                      ${displaystyle 4z^{11}+124z^{12}+1539z^{13}+...+33385461z^{46}+2707075z^{47}}$;

Die längsten derartigen Pfade sind also Hamilton-Pfade mit einer Größe von 2.707.075. ZDDs sind in diesem Fall für einfache Pfade und Hamilton-Pfade effizient.

das Problem der Acht Königinnen[edit]

Definieren Sie 64 Eingabevariablen, um die Quadrate auf einem Schachbrett darzustellen. Jede Variable bezeichnet die Anwesenheit oder Abwesenheit einer Königin auf diesem Feld. Berücksichtige das,

• In einer bestimmten Spalte ist nur eine Variable "1".
• In einer bestimmten Zeile ist nur eine Variable "1".
• Auf einer bestimmten diagonalen Linie ist eine oder keine Variable "1".

Obwohl man dieses Problem durch die Konstruktion von OBDDs lösen kann, ist es effizienter, ZDDs zu verwenden. Die Erstellung eines ZDD für das 8-Queens-Problem erfordert 8 Schritte von S1 bis S8. Jeder Schritt kann wie folgt definiert werden:

S1: Repräsentiert alle Möglichkeiten, eine Königin in die erste Reihe zu setzen.

S2: Repräsentiert alle Möglichkeiten, eine Königin in die zweite Reihe zu setzen, um die erste Königin nicht zu verletzen.

S3: Stellt alle Möglichkeiten dar, eine Königin in die dritte Reihe zu setzen, damit die vorherigen Königinnen nicht verletzt werden.

…

S8: Stellt alle Möglichkeiten dar, eine Königin in die achte Reihe zu setzen, damit sie nicht gegen die vorherigen Königinnen verstößt.

Das ZDD für S8 besteht aus allen möglichen Lösungen des 8-Queens-Problems. Für dieses spezielle Problem kann das Zwischenspeichern die Leistung des Algorithmus erheblich verbessern. Die Verwendung des Cache zur Vermeidung von Duplikaten kann die N-Queens-Probleme bis zu 4,5-mal schneller verbessern als die Verwendung der nur grundlegenden Operationen (wie oben definiert) (siehe Abbildung 10).

Das Tourproblem des Ritters[edit]

Das Tourproblem des Ritters hat eine historische Bedeutung. Die Grafik des Ritters enthält n2 Eckpunkte zur Darstellung der Quadrate des Schachbretts. Die Kanten veranschaulichen die legalen Bewegungen eines Ritters. Der Ritter kann jedes Feld des Bretts genau einmal besuchen. Olaf Schröer, M. Löbbing und Ingo Wegener näherten sich diesem Problem, und zwar auf einer Tafel, indem sie jeder Kante im Diagramm Boolesche Variablen zuweisen, wobei insgesamt 156 Variablen zur Bezeichnung aller Kanten verwendet wurden. Eine Lösung des Problems kann durch einen 156-Bit-Kombinationsvektor ausgedrückt werden. Laut Minato ist der Aufbau eines ZDD für alle Lösungen zu groß, um direkt gelöst zu werden. Es ist einfacher zu teilen und zu erobern. Durch Aufteilen der Probleme in zwei Teile des Boards und Erstellen von ZDDs in Teilräumen kann das Tourproblem von The Knight mit jeder Lösung mit 64 Kanten gelöst werden. Da der Graph jedoch nicht sehr dünn ist, ist der Vorteil der Verwendung von ZDDs nicht so offensichtlich.

Fehlersimulation[edit]

N. Takahashi et al. Schlugen eine Fehlersimulationsmethode für mehrere Fehler unter Verwendung von OBDDs vor. Diese deduktive Methode überträgt die Fehlersätze von den primären Eingängen zu den primären Ausgängen und erfasst die Fehler an den primären Ausgängen. Da diese Methode unate Cube-Set-Ausdrücke umfasst, sind ZDDs effizienter. Die Optimierungen von ZDDs in Unate-Cube-Set-Berechnungen zeigen, dass ZDDs bei der Entwicklung von VLSI-CAD-Systemen und in einer Vielzahl anderer Anwendungen nützlich sein könnten.

Siehe auch[edit]

Verfügbare Pakete[edit]

• CUDD: Ein in C geschriebenes BDD-Paket, das BDDs und ZBDDs implementiert, University of Colorado, Boulder
• JDD, Eine Java-Bibliothek, die allgemeine BDD- und ZBDD-Operationen implementiert
• Graphillion, Eine auf Python basierende ZDD-Softwareimplementierung
• [1], Eine CWEB ZDD-Implementierung von Donald Knuth.

Verweise[edit]

• Shin-ichi Minato, "Null-unterdrückte BDDs zur Manipulation von Sätzen bei kombinatorischen Problemen", DAC '93: Vorträge der 30. internationalen Konferenz über Designautomatisierung, 1993
• CH. Meinel, T. Theobald, "Algorithmen und Datenstrukturen im VLSI-Design: OBDD - Grundlagen und Anwendungen ", Springer-Verlag, Berlin, Heidelberg, New York, 1998.
• Minato, Shin-ichi. "Null-unterdrückte BDDs und ihre Anwendungen." https://eprints.lib.hokudai.ac.jp/dspace/bitstream/2115/16895/1/IJSTTT3-2.pdf, Hokkaido University, Mai 2001, https://eprints.lib.hokudai.ac.jp/dspace/bitstream/2115/16895/1/IJSTTT3-2.pdf.
• Minato, Shin-ichi. "Null unterdrückte BDDs für die Manipulation von Sätzen bei kombinatorischen Problemen." 1993, doi:https://pdfs.semanticscholar.org/9593/6223362a16a50de2959475d87aefe2a1fec7.pdf.
• Bryant, Randal E. "Binäre Entscheidungsdiagramme und darüber hinaus: Ermöglichung von Technologien für die formale Überprüfung." http://Repository.cmu.edu/Cgi/Viewcontent.cgi?Article=1245&Context=Compsci, Carnegie Mellon University, November 1995, repository.cmu.edu/cgi/viewcontent.cgi?article=1245&context=compsci.
• Lynn, Ben. "ZDDs." ZDDs - Einführung, Stanford University, 2005, crypto.stanford.edu/pbc/notes/zdd/.
• Mischchenko, Alan. "Eine Einführung in Null-unterdrückte binäre Entscheidungsdiagramme." 5. Februar 2014, doi:https://people.eecs.berkeley.edu/~alanmi/publications/2001/tech01_zdd_.pdf.
• Knuth, Donald E. Die Kunst der Computerprogrammierung, Band 4. 22. Dezember 2008.

Externe Links[edit]

• Minato, Shin-ichi. "Null-unterdrückte BDDs und ihre Anwendungen." https://Www.researchgate.net/Profile/Shin-ichi_Minato/Publication/37555760_Zero-suppressed_BDDs_and_their_applications/Links/02e7e52b85cd639cb5000000.Pdf, Hokkaido University, Mai 2001, www.researchgate.net/profile/Shin-ichi_Minato/publication/37555760_Zero-suppressed_BDDs_and_their_applications/links/02e7e52b85cd639cb5000000.pdf.
• Minato, Shin-ichi. "Null unterdrückte BDDs für die Manipulation von Sätzen bei kombinatorischen Problemen." 1993, doi:https://pdfs.semanticscholar.org/9593/6223362a16a50de2959475d87aefe2a1fec7.pdf.
• Bryant, Randal E. "Binäre Entscheidungsdiagramme und darüber hinaus: Ermöglichung von Technologien für die formale Überprüfung." http://Repository.cmu.edu/Cgi/Viewcontent.cgi?Article=1245&Context=Compsci, Carnegie Mellon University, November 1995, repository.cmu.edu/cgi/viewcontent.cgi?article=1245&context=compsci.
• Lynn, Ben. "ZDDs." ZDDs - Einführung, Stanford University, 2005, crypto.stanford.edu/pbc/notes/zdd/.
• Alan Mishchenko, Alan. "Eine Einführung in nullunterdrückte binäre Entscheidungsdiagramme." 5. Februar 2014, doi:https://people.eecs.berkeley.edu/~alanmi/publications/2001/tech01_zdd_.pdf.
• Alan Mishchenko, Eine Einführung in nullunterdrückte binäre Entscheidungsdiagramme
• Donald Knuth, Spaß mit nullunterdrückten binären Entscheidungsdiagrammen (ZDDs) (Videovorlesung, 2008)
• Minato Shin-ichi, Pfade in Graphen zählen (Grundlagen des ZDD) (Videoillustration auf Miraikan)