Inversive Geometrie – Wikipedia

Posted on November 28, 2020 by lordneo

before-content-x4

In der Geometrie inversive Geometrie ist die Untersuchung jener Eigenschaften von Figuren, die durch eine Verallgemeinerung einer Art von Transformation der euklidischen Ebene erhalten werden, genannt Inversion. Diese Transformationen bewahren Winkel und ordnen verallgemeinerte Kreise verallgemeinerten Kreisen zu, wobei a verallgemeinerter Kreis bedeutet entweder einen Kreis oder eine Linie (lose gesagt, ein Kreis mit unendlichem Radius). Viele schwierige Probleme in der Geometrie werden viel leichter zu lösen, wenn eine Inversion angewendet wird.

after-content-x4

Das Konzept der Inversion kann auf höherdimensionale Räume verallgemeinert werden.

Inversion im Kreis [edit]

Umkehrung eines Punktes[edit]

P.‘ ist die Umkehrung von P. in Bezug auf den Kreis.

Eine Zahl in der Arithmetik zu invertieren bedeutet normalerweise, ihren Kehrwert zu nehmen. Eine eng verwandte Idee in der Geometrie ist das “Invertieren” eines Punktes. Im Flugzeug ist die invers eines Punktes P. in Bezug auf a Referenzkreis (Ø) mit Mitte Ö und Radius r ist ein Punkt P.‘, auf dem Strahl liegend von Ö durch P. so dass

{ displaystyle OP cdot OP ^ { prime} = r ^ {2}.}

Das nennt man Kreisinversion oder Ebeneninversion. Die Umkehrung nimmt irgendeinen Punkt P. (außer Ö) zu seinem Bild P.‘ nimmt auch P.‘ zurück zu P.Das Ergebnis der zweimaligen Anwendung derselben Inversion ist also die Identitätstransformation auf allen Punkten der Ebene außer Ö (Selbstinversion).^[1]^[2] Um die Inversion zu einer Involution zu machen, ist es notwendig, einen Punkt im Unendlichen einzuführen, einen einzelnen Punkt, der auf allen Linien platziert ist, und die Inversion per Definition zu erweitern, um das Zentrum auszutauschen Ö und dieser Punkt im Unendlichen.

Aus der Definition folgt, dass die Umkehrung eines Punktes innerhalb des Referenzkreises außerhalb des Kreises liegen muss und umgekehrt, wobei sich der Mittelpunkt und der Punkt an unendlich wechselnden Positionen befinden, während jeder Punkt auf dem Kreis nicht beeinflusst wird (ist) invariant unter Inversion). Zusammenfassend lässt sich sagen, je näher ein Punkt am Zentrum liegt, desto weiter entfernt ist seine Transformation und umgekehrt.

after-content-x4

Kompass- und Linealkonstruktion[edit]

Punkt außerhalb des Kreises

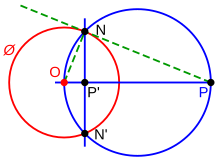
Umkehrung zu konstruieren P.‘ eines Punktes P. außerhalb eines Kreises Ö: Lassen r sei der Radius von Ö. Rechtecke OPN und AUF P‘ sind ähnlich. OP ist zu r wie r ist zu OP‘.

Umkehrung zu konstruieren P.‘ eines Punktes P. außerhalb eines Kreises Ö::

Zeichnen Sie das Segment aus Ö (Mittelpunkt des Kreises Ö) bis P..
Lassen M. sei der Mittelpunkt von OP.
Zeichne den Kreis c mit Mitte M. durchgehen P..
Lassen N. und N.‘ seien Sie die Punkte, an denen Ö und c schneiden.
Segment zeichnen NN‘.
P.‘ ist wo OP und NN‘ schneiden.

Zeigen Sie innerhalb des Kreises

Umkehrung zu konstruieren P. eines Punktes P.‘ innerhalb eines Kreises Ö::

Strahl zeichnen r von Ö (Mittelpunkt des Kreises Ö) durch P.‘.
Linie zeichnen s durch P.‘ senkrecht zu r.
Lassen N. sei einer der Punkte wo Ö und s schneiden.
Zeichnen Sie das Segment AUF.
Linie zeichnen t durch N. senkrecht zu AUF.
P. ist wo Strahl r und Linie t schneiden.

Duttas Bau[edit]

Es gibt eine Konstruktion des Umkehrpunktes zu EIN in Bezug auf einen Kreis P. das ist unabhängig von ob EIN ist drinnen oder draußen P..^[3]

Betrachten Sie einen Kreis P. mit Mitte Ö und ein Punkt EIN die innerhalb oder außerhalb des Kreises liegen können P..

Nehmen Sie den Schnittpunkt C. des Strahls OA mit dem Kreis P..
Verbinden Sie den Punkt C. mit einem beliebigen Punkt B. auf dem Kreis P. (anders als C.)
Reflektiere den Strahl BA in der Schlange BC und lass h sei die Reflexion, die den Strahl schneidet OK in einem Punkt EIN‘. EIN‘ist der Umkehrpunkt von EIN in Bezug auf Kreis P..^[3]^{::§ 3.2}

Eigenschaften[edit]

Die Umkehrung eines durchlaufenden Kreises in Bezug auf den roten Kreis Ö (blau) ist eine Linie, die nicht durchgeht Ö (grün) und umgekehrt.
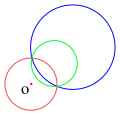
Die Umkehrung eines Kreises in Bezug auf den roten Kreis nicht durchgehen Ö (blau) ist ein Kreis, der nicht durchgeht Ö (grün) und umgekehrt.
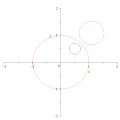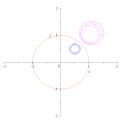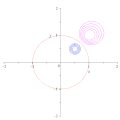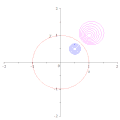
Durch Inversion in Bezug auf einen Kreis wird der Mittelpunkt des Kreises nicht dem Mittelpunkt seines Bildes zugeordnet

Die Umkehrung einer Menge von Punkten in der Ebene in Bezug auf einen Kreis ist die Menge der Umkehrungen dieser Punkte. Die folgenden Eigenschaften machen die Kreisinversion nützlich.

Ein Kreis, der durch die Mitte verläuft Ö des Referenzkreises invertiert sich zu einer Linie, die nicht durchgeht Ö, aber parallel zur Tangente an den ursprünglichen Kreis bei Ö, und umgekehrt; während eine Linie durch Ö ist in sich selbst invertiert (aber nicht punktweise invariant).^[4]
Ein Kreis, der nicht durchgeht Ö kehrt sich zu einem Kreis um, der nicht durchgeht Ö. Wenn der Kreis auf den Referenzkreis trifft, befinden sich diese invarianten Schnittpunkte auch auf dem umgekehrten Kreis. Ein Kreis (oder eine Linie) bleibt durch Inversion genau dann unverändert, wenn er an den Schnittpunkten orthogonal zum Referenzkreis ist.^[5]

Zusätzliche Eigenschaften umfassen:

Wenn ein Kreis q durchläuft zwei verschiedene Punkte A und A ‘, die in Bezug auf einen Kreis umgekehrt sind kdann die Kreise k und q sind orthogonal.
Wenn die Kreise k und q sind orthogonal, dann verläuft eine gerade Linie durch das Zentrum O von k und sich überschneiden qtut dies an inversen Punkten in Bezug auf k.
Gegeben ist ein Dreieck OAB, in dem O der Mittelpunkt eines Kreises ist kund Punkte A ‘und B’ kehren A und B in Bezug auf um k, dann

{ displaystyle angle OAB = angle OB’A ‘ { text {und}} angle OBA = angle OA’B’.}

Die Schnittpunkte zweier Kreise p und q orthogonal zu einem Kreis ksind invers in Bezug auf k.
Wenn M und M ‘inverse Punkte in Bezug auf einen Kreis sind k auf zwei Kurven m und m ‘auch umgekehrt in Bezug auf kdann sind die Tangenten an m und m ‘an den Punkten M und M’ entweder senkrecht zur Geraden MM ‘oder bilden mit dieser Linie ein gleichschenkliges Dreieck mit der Basis MM’.
Die Inversion lässt das Winkelmaß unverändert, kehrt jedoch die Ausrichtung der orientierten Winkel um.^[6]

Beispiele in zwei Dimensionen[edit]

Beispiele für die Inversion der Kreise A bis J in Bezug auf den roten Kreis bei O. Kreise A bis F, die durch die O-Karte zu geraden Linien verlaufen. Kreise G bis J, die nicht anderen Kreisen zugeordnet sind. Der Referenzkreis und die Linie L sind auf sich selbst abgebildet. Kreise schneiden ihre Umkehrungen, falls vorhanden, auf dem Referenzkreis. Im die SVG-Datei, Klicken oder bewegen Sie den Mauszeiger über einen Kreis, um ihn hervorzuheben.

Die Inversion einer Linie ist ein Kreis, der den Inversionsmittelpunkt enthält. oder es ist die Linie selbst, wenn sie die Mitte enthält
Die Umkehrung eines Kreises ist ein anderer Kreis; oder es ist eine Linie, wenn der ursprüngliche Kreis den Mittelpunkt enthält
Die Inversion einer Parabel ist eine Niere
Die Inversion der Hyperbel ist eine Lemniskate von Bernoulli

Anwendung[edit]

Bei einem Kreis, der nicht durch das Inversionszentrum verläuft, sind der Mittelpunkt des Kreises, der invertiert wird, und der Mittelpunkt seines Bildes unter Inversion kollinear mit dem Mittelpunkt des Referenzkreises. Diese Tatsache kann verwendet werden, um zu beweisen, dass die Euler-Linie des Intouch-Dreiecks eines Dreiecks mit seiner OI-Linie übereinstimmt. Der Beweis lautet ungefähr wie folgt:

Invertieren in Bezug auf den Kreis des Dreiecks ABC. Das mediale Dreieck des Intouch-Dreiecks wird in ein Dreieck umgewandelt ABCDies bedeutet den Umfang des medialen Dreiecks, dh das Neun-Punkte-Zentrum des intouch-Dreiecks, den Mittelpunkt und den Umfang des Dreiecks ABC sind kollinear.

Zwei beliebige sich nicht schneidende Kreise können in konzentrische Kreise invertiert werden. Dann wird der inversive Abstand (üblicherweise mit δ bezeichnet) als natürlicher Logarithmus des Verhältnisses der Radien der beiden konzentrischen Kreise definiert.

Zusätzlich können zwei beliebige nicht schneidende Kreise unter Verwendung eines Inversionskreises, der an einem Punkt auf dem Kreis der Antisimilitude zentriert ist, in kongruente Kreise invertiert werden.

Die Peaucellier-Lipkin-Verknüpfung ist eine mechanische Implementierung der Inversion in einem Kreis. Es bietet eine genaue Lösung für das wichtige Problem der Umwandlung zwischen linearer und kreisförmiger Bewegung.

Pol und Polar[edit]

Die Polarlinie q bis zu einem Punkt Q. in Bezug auf einen Kreis mit Radius r zentriert auf den Punkt Ö. Der Punkt P. ist der Inversionspunkt von Q.;; Die Polarität ist die Linie durch P. das ist senkrecht zu der Linie, die enthält Ö, P. und Q..

Wenn Punkt R. ist die Umkehrung des Punktes P. dann die Linien senkrecht zur Linie PR durch einen der Punkte ist die Polarität des anderen Punktes (der Pol).

Pole und Polare haben mehrere nützliche Eigenschaften:

Wenn ein Punkt P. liegt auf einer Linie l, dann die Stange L. der Linie l liegt am polaren p von Punkt P..
Wenn ein Punkt P. bewegt sich entlang einer Linie l, es ist polar p dreht sich um die Stange L. der Linie l.
Wenn zwei Tangentenlinien von einem Pol zum Kreis gezogen werden können, verläuft seine Polarität durch beide Tangentenpunkte.
Wenn ein Punkt auf dem Kreis liegt, ist seine Polarität die Tangente durch diesen Punkt.
Wenn ein Punkt P. liegt also auf seiner eigenen Polarlinie P. ist auf dem Kreis.
Jede Linie hat genau einen Pol.

In drei Dimensionen[edit]

Inversion einer Kugel an der roten Kugel

Inversion eines Sphäroids (an der roten Kugel)

Inversion eines Hyperboloids eines Blattes

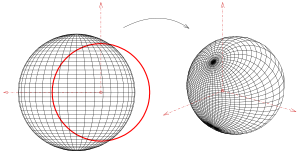
Die Kreisinversion ist auf die dreidimensionale Kugelinversion verallgemeinerbar. Die Umkehrung eines Punktes P. in 3D in Bezug auf eine Referenzkugel, die an einem Punkt zentriert ist Ö mit Radius R. ist ein Punkt P. ‘ so dass

{ displaystyle OP times OP ^ { prime} = R ^ {2}}

${ displaystyle OP times OP ^ { prime} = R ^ {2}}$ und die Punkte P. und P. ‘sind auf dem gleichen Strahl ab Ö. Wie bei der 2D-Version wird eine Kugel in eine Kugel invertiert, außer wenn eine Kugel durch das Zentrum verläuft Ö der Referenzkugel kehrt sie dann in eine Ebene um. Jedes Flugzeug, das nicht durchfliegt Ö, kehrt sich zu einer Kugel um, die sich berührt Ö. Ein Kreis, dh der Schnittpunkt einer Kugel mit einer Sekantenebene, kehrt sich in einen Kreis um, außer wenn der Kreis durchläuft Ö es invertiert sich in eine Linie. Dies reduziert sich auf den 2D-Fall, wenn die Sekantenebene durchläuft Ö, ist aber ein echtes 3D-Phänomen, wenn die Sekantenebene nicht durchläuft Ö.

Beispiele in drei Dimensionen[edit]

Kugel[edit]

Die einfachste Oberfläche (neben einer Ebene) ist die Kugel. Das erste Bild zeigt eine nicht triviale Inversion (der Mittelpunkt der Kugel ist nicht der Mittelpunkt der Inversion) einer Kugel zusammen mit zwei orthogonal sich kreuzenden Bleistiftstiften.

Zylinder, Kegel, Torus[edit]

Die Inversion eines Zylinders, Kegels oder Torus führt zu einem Dupin-Cyclid.

Sphäroid[edit]

Ein Sphäroid ist eine Rotationsfläche und enthält einen Kreisstift, der auf einen Kreisstift abgebildet ist (siehe Bild). Das inverse Bild eines Sphäroids ist eine Oberfläche vom Grad 4.

Hyperboloid eines Blattes[edit]

Ein Hyperboloid eines Blattes, das eine Rotationsfläche darstellt, enthält einen Kreisstift, der auf einen Kreisstift abgebildet wird. Ein Hyperboloid eines Blattes enthält zusätzlich zwei Linienstifte, die auf Kreisstifte abgebildet werden. Das Bild zeigt eine solche Linie (blau) und ihre Umkehrung.

Stereographische Projektion als Umkehrung einer Kugel[edit]

Stereographische Projektion als Umkehrung einer Kugel

Eine stereografische Projektion projiziert normalerweise eine Kugel von einem Punkt aus

{ displaystyle N}

$N.$ (Nordpol) der Kugel auf die Tangentialebene am gegenüberliegenden Punkt

{ displaystyle S}

$S.$ (Südpol). Diese Abbildung kann durch Inversion der Kugel auf ihre Tangentialebene durchgeführt werden. Wenn die Kugel (die projiziert werden soll) die Gleichung hat

{ displaystyle x ^ {2} + y ^ {2} + z ^ {2} = – z}

${ displaystyle x ^ {2} + y ^ {2} + z ^ {2} = - z}$ (abwechselnd geschrieben

{ displaystyle x ^ {2} + y ^ {2} + (z + { tfrac {1} {2}}) ^ {2} = { tfrac {1} {4}}}

${ displaystyle x ^ {2} + y ^ {2} + (z + { tfrac {1} {2}}) ^ {2} = { tfrac {1} {4}}}$ ;; Center

{ displaystyle (0,0, -0,5)}

${ displaystyle (0,0, -0,5)}$ Radius

{ displaystyle 0.5}

$0,5$ , grün im Bild), dann wird es durch die Inversion an der Einheitskugel (rot) auf die Tangentialebene am Punkt abgebildet

{ displaystyle S = (0,0, -1)}

${ displaystyle S = (0,0, -1)}$ . Die Linien durch das Inversionszentrum (Punkt

{ displaystyle N}

$N.$ ) sind auf sich selbst abgebildet. Sie sind die Projektionslinien der stereografischen Projektion.

6-Kugel-Koordinaten[edit]

Die 6-Kugel-Koordinaten sind ein Koordinatensystem für den dreidimensionalen Raum, das durch Invertieren der kartesischen Koordinaten erhalten wird.

Axiomatik und Verallgemeinerung[edit]

Eine der ersten, die sich mit Grundlagen der inversiven Geometrie befasste, war Mario Pieri in den Jahren 1911 und 1912.^[7]Edward Kasner schrieb seine Dissertation über “Invariante Theorie der Inversionsgruppe”.^[8]

In jüngerer Zeit wurde die mathematische Struktur der inversiven Geometrie als Inzidenzstruktur interpretiert, bei der die verallgemeinerten Kreise als “Blöcke” bezeichnet werden: In der Inzidenzgeometrie bildet jede affine Ebene zusammen mit einem einzelnen Punkt im Unendlichen eine Möbius-Ebene, auch bekannt als inversive Ebene. Der Punkt im Unendlichen wird allen Linien hinzugefügt. Diese Möbius-Ebenen können axiomatisch beschrieben werden und existieren sowohl in endlichen als auch in unendlichen Versionen.

Ein Modell für die Möbius-Ebene, die aus der euklidischen Ebene stammt, ist die Riemann-Kugel.

Invariant[edit]

Das Kreuzverhältnis zwischen 4 Punkten

{ displaystyle x, y, z, w}

${ displaystyle x, y, z, w}$ ist unter einer Inversion invariant. Insbesondere wenn O das Zentrum der Inversion ist und

{ displaystyle r_ {1}}

$r_ {1}$ und

{ displaystyle r_ {2}}

$r_ {2}$ sind Abstände zu den Enden einer Linie L, dann Länge der Linie

{ displaystyle d}

$d$ wird werden

{ displaystyle d / (r_ {1} r_ {2})}

${ displaystyle d / (r_ {1} r_ {2})}$ unter einer Inversion mit Zentrum O. Die Invariante ist:

{ displaystyle I = { frac {| xy || wz |} {| xw || yz |}}}

Beziehung zum Erlangen-Programm[edit]

Laut Coxeter^[9] Die Transformation durch Inversion im Kreis wurde 1831 von LI Magnus erfunden. Seitdem ist diese Abbildung ein Weg zur höheren Mathematik. Durch einige Schritte der Anwendung der Kreisinversionskarte erkennt ein Student der Transformationsgeometrie bald die Bedeutung von Felix Kleins Erlangen-Programm, einem Ergebnis bestimmter Modelle der hyperbolischen Geometrie

Erweiterung[edit]

Die Kombination von zwei Inversionen in konzentrischen Kreisen führt zu einer Ähnlichkeit, homothetischen Transformation oder Dilatation, die durch das Verhältnis der Kreisradien gekennzeichnet ist.

{ displaystyle x mapsto R ^ {2} { frac {x} {| x | ^ {2}}} = y mapsto T ^ {2} { frac {y} {| y | ^ {2} }} = left ({ frac {T} {R}} right) ^ {2} x.}

Gegenbewegung[edit]

Wenn ein Punkt in der Ebene als komplexe Zahl interpretiert wird

{ displaystyle z = x + iy,}

$z = x + iy,$ mit komplexem Konjugat

{ displaystyle { bar {z}} = x-iy,}

${ displaystyle { bar {z}} = x-iy,}$ dann das Gegenteil von z ist

{ displaystyle { frac {1} {z}} = { frac { bar {z}} {| z | ^ {2}}}.}

Folglich ist die algebraische Form der Inversion in einem Einheitskreis gegeben durch

{ displaystyle z mapsto w}

$z mapsto w$ wo:

{ displaystyle w = { frac {1} { bar {z}}} = { overline { left ({ frac {1} {z}} right)}}}

Die Hin- und Herbewegung ist der Schlüssel in der Transformationstheorie als Generator der Möbius-Gruppe. Die anderen Generatoren sind Translation und Rotation, die beide durch physikalische Manipulationen im umgebenden 3-Raum bekannt sind. Die Einführung der Hin- und Herbewegung (abhängig von der Kreisinversion) erzeugt die Besonderheit der Möbius-Geometrie, die manchmal mit der inversiven Geometrie (der euklidischen Ebene) identifiziert wird. Inversive Geometrie ist jedoch die größere Studie, da sie die rohe Inversion in einem Kreis enthält (noch nicht konjugiert in Hin- und Herbewegung). Inversive Geometrie umfasst auch die Konjugationsabbildung. Weder Konjugation noch Inversion im Kreis gehören zur Möbius-Gruppe, da sie nicht konform sind (siehe unten). Möbius-Gruppenelemente sind analytische Funktionen der gesamten Ebene und daher notwendigerweise konform.

Kreise in Kreise verwandeln[edit]

Betrachten Sie in der komplexen Ebene den Radiuskreis

{ displaystyle r}

$r$ um den Punkt

{ displaystyle a}

$ein$

{ displaystyle (za) (za) ^ {*} = r ^ {2}}

wo ohne Verlust der Allgemeinheit,

{ displaystyle a in mathbb {R}.}

${ displaystyle a in mathbb {R}.}$ Verwendung der Definition der Inversion

{ displaystyle w = { frac {1} {z ^ {*}}}

es ist einfach, das zu zeigen

{ displaystyle w}

$w$ gehorcht der Gleichung

{ displaystyle ww ^ {*} – { frac {a} {(a ^ {2} -r ^ {2})}} (w + w ^ {*}) + { frac {a ^ {2} } {(a ^ {2} -r ^ {2}) ^ {2}} = { frac {r ^ {2}} {(a ^ {2} -r ^ {2}) ^ {2} }}}

und daher das

{ displaystyle w}

$w$ beschreibt den Mittelpunktskreis

{ textstyle { frac {a} {a ^ {2} -r ^ {2}}}}

${ textstyle { frac {a} {a ^ {2} -r ^ {2}}}}$ und Radius

{ textstyle { frac {r} {| a ^ {2} -r ^ {2} |}}.}

${ textstyle { frac {r} {| a ^ {2} -r ^ {2} |}}.}$

Wann

{ displaystyle a to r,}

${ displaystyle a to r,}$ Der Kreis verwandelt sich in eine Linie parallel zur imaginären Achse

{ displaystyle w + w ^ {*} = { tfrac {1} {a}}.}

${ displaystyle w + w ^ {*} = { tfrac {1} {a}}.}$

Zum

{ displaystyle a not in mathbb {R}}

${ displaystyle a not in mathbb {R}}$ und

{ displaystyle aa ^ {*} neq r ^ {2}}

${ displaystyle aa ^ {*} neq r ^ {2}}$ das Ergebnis für

{ displaystyle w}

$w$ ist

{ displaystyle { begin {align} & ww ^ {*} – { frac {aw + a ^ {*} w ^ {*}} {(a ^ {*} ar ^ {2})}} + { frac {aa ^ {*}} {(aa ^ {*} – r ^ {2}) ^ {2}}} = { frac {r ^ {2}} {(aa ^ {*} – r ^ { 2}) ^ {2}}} \[4pt] Longleftrightarrow {} & left (w – { frac {a ^ {*}} {aa ^ {*} – r ^ {2}}} right) left (w ^ {*} – { frac { a} {a ^ {*} ar ^ {2}}} right) = left ({ frac {r} { left | aa ^ {*} – r ^ {2} right |}} right ) ^ {2} end {align}}}

zeigt, dass die

{ displaystyle w}

$w$ beschreibt den Mittelpunktskreis

{ textstyle { frac {a ^ {*}} {(aa ^ {*} – r ^ {2})}}}

${ textstyle { frac {a ^ {*}} {(aa ^ {*} - r ^ {2})}}}$ und Radius

{ textstyle { frac {r} { left | a ^ {*} ar ^ {2} right |}}}

${ textstyle { frac {r} { left | a ^ {*} ar ^ {2} right |}}}$ .

Wann

{ displaystyle a ^ {*} a to r ^ {2},}

${ displaystyle a ^ {*} a to r ^ {2},}$ die Gleichung für

{ displaystyle w}

$w$ wird

{ displaystyle { begin {align} & aw + a ^ {*} w ^ {*} = 1 Longleftrightarrow 2 operatorname {Re} {aw } = 1 Longleftrightarrow operatorname {Re} {a } operatorname {Re} {w } – operatorname {Im} {a } operatorname {Im} {w } = { frac {1} {2}} \[4pt] Longleftrightarrow {} & operatorname {Im} {w } = { frac { operatorname {Re} {a }} { operatorname {Im} {a }} cdot operatorname {Re } {w } – { frac {1} {2 cdot operatorname {Im} {a }}}. end {align}}}

Höhere Geometrie[edit]

Wie oben erwähnt, erfordert Null, der Ursprung, eine besondere Berücksichtigung bei der Kreisinversionsabbildung. Der Ansatz besteht darin, an einen Punkt im Unendlichen zu grenzen, der mit ∞ oder 1/0 bezeichnet ist. Bei dem Ansatz mit komplexen Zahlen, bei dem die Hin- und Herbewegung die scheinbare Operation ist, führt dieses Verfahren zu der komplexen Projektionslinie, die häufig als Riemann-Kugel bezeichnet wird. Es waren Unterräume und Untergruppen dieses Raums und eine Gruppe von Abbildungen, die angewendet wurden, um frühe Modelle der hyperbolischen Geometrie von Beltrami, Cayley und Klein zu erstellen. Inversive Geometrie schließt also die Ideen von Lobachevsky und Bolyai in ihre Ebenengeometrie ein. Darüber hinaus war Felix Klein von dieser Möglichkeit der Abbildung, geometrische Phänomene zu identifizieren, so überwältigt, dass er 1872 ein Manifest, das Erlangen-Programm, lieferte. Seitdem behalten sich viele Mathematiker den Begriff vor Geometrie für einen Raum zusammen mit einer Gruppe von Abbildungen dieses Raumes. Die signifikanten Eigenschaften von Figuren in der Geometrie sind diejenigen, die unter dieser Gruppe unveränderlich sind.

Zum Beispiel Smogorzhevsky^[10] entwickelt mehrere Theoreme der inversiven Geometrie, bevor mit der Lobachevskschen Geometrie begonnen wird.

In höheren Dimensionen[edit]

Im n-dimensionaler Raum, in dem sich eine Kugel mit Radius befindet r, Inversion in der Kugel ist gegeben durch

{ displaystyle x_ {i} mapsto { frac {r ^ {2} x_ {i}} { sum _ {j} x_ {j} ^ {2}}}

Die Transformation durch Inversion in Hyperebenen oder Hypersphären in E.ⁿ kann verwendet werden, um Dilatationen, Translationen oder Rotationen zu erzeugen. In der Tat führen zwei konzentrische Hypersphären, die zur Erzeugung aufeinanderfolgender Inversionen verwendet werden, zu einer Erweiterung oder Kontraktion des Hypersphärenzentrums. Eine solche Abbildung wird als Ähnlichkeit bezeichnet.

Wenn zwei parallele Hyperebenen verwendet werden, um aufeinanderfolgende Reflexionen zu erzeugen, ist das Ergebnis eine Übersetzung. Wenn sich zwei Hyperebenen in einem (n–2) -flache, aufeinanderfolgende Reflexionen erzeugen eine Rotation, bei der jeder Punkt der (n–2) -flach ist ein fester Punkt jeder Reflexion und damit der Zusammensetzung.

All dies sind konforme Karten. Wenn der Raum drei oder mehr Dimensionen hat, sind die durch Inversion erzeugten Zuordnungen die einzigen konformen Zuordnungen. Der Satz von Liouville ist ein klassischer Satz der konformen Geometrie.

Das Hinzufügen eines Punktes im Unendlichen zum Raum vermeidet die Unterscheidung zwischen Hyperebene und Hypersphäre; Eine höherdimensionale inversive Geometrie wird dann häufig im vermuteten Kontext eines untersucht n-Kugel als Basisraum. Die Transformationen der inversiven Geometrie werden oft als Möbius-Transformationen bezeichnet. Inversive Geometrie wurde angewendet, um Färbungen oder Trennwände eines zu untersuchen n-Kugel.^[11]

Antikonformale Zuordnungseigenschaft[edit]

Die Kreisinversionskarte ist antikonform, was bedeutet, dass an jedem Punkt Winkel beibehalten und die Ausrichtung umgekehrt werden (eine Karte wird als konform bezeichnet, wenn sie erhalten bleibt orientiert Winkel). Algebraisch gesehen ist eine Karte antikonform, wenn an jedem Punkt der Jacobi ein Skalar mal eine orthogonale Matrix mit negativer Determinante ist: In zwei Dimensionen muss der Jacobian ein Skalar mal eine Reflexion an jedem Punkt sein. Dies bedeutet, dass wenn J. ist also der Jakobianer

{ displaystyle J cdot J ^ {T} = kI}

${ displaystyle J cdot J ^ {T} = kI}$ und

{ displaystyle det (J) = – { sqrt {k}}.}

${ displaystyle det (J) = - { sqrt {k}}.}$ Berechnung des Jacobian in dem Fall z_ich = x_ich/ ||x||², wo ||x||² = x₁² + … + x_n² gibt JJ^T. = kImit k = 1 / ||x||⁴und zusätzlich det (J.) ist negativ; daher ist die inversive Karte antikonformal.

In der komplexen Ebene ist die offensichtlichste Kreisinversionskarte (dh unter Verwendung des am Ursprung zentrierten Einheitskreises) das komplexe Konjugat der komplexen inversen Kartenaufnahme z bis 1/z. Die komplexe analytische inverse Karte ist konform und ihre konjugierte Kreisinversion ist antikonform. In diesem Fall ist eine Homographie konform, während eine Antihomographie antikonform ist.

Inversive Geometrie und hyperbolische Geometrie[edit]

Das (n – 1) -Kugel mit Gleichung

{ displaystyle x_ {1} ^ {2} + cdots + x_ {n} ^ {2} + 2a_ {1} x_ {1} + cdots + 2a_ {n} x_ {n} + c = 0}

wird einen positiven Radius haben, wenn ein₁² + … + ein_n² ist größer als cund bei Inversion gibt die Kugel

{ displaystyle x_ {1} ^ {2} + cdots + x_ {n} ^ {2} +2 { frac {a_ {1}} {c}} x_ {1} + cdots +2 { frac {a_ {n}} {c}} x_ {n} + { frac {1} {c}} = 0.}

Daher ist es unter Inversion genau dann unveränderlich, wenn c = 1. Dies ist jedoch die Bedingung, orthogonal zur Einheitskugel zu sein. Daher werden wir veranlasst, die (n – 1) -Kugeln mit Gleichung

{ displaystyle x_ {1} ^ {2} + cdots + x_ {n} ^ {2} + 2a_ {1} x_ {1} + cdots + 2a_ {n} x_ {n} + 1 = 0}

die unter Inversion invariant sind, orthogonal zur Einheitskugel sind und Zentren außerhalb der Kugel haben. Diese bilden zusammen mit den Subraum-Hyperebenen, die die Hemisphären trennen, die Hyperflächen des Poincaré-Scheibenmodells der hyperbolischen Geometrie.

Da die Inversion in der Einheitskugel die zu ihr orthogonalen Kugeln unveränderlich lässt, ordnet die Inversion die Punkte innerhalb der Einheitskugel nach außen und umgekehrt zu. Dies gilt daher im Allgemeinen für orthogonale Kugeln, und insbesondere für die Inversion in einer der zur Einheitskugel orthogonalen Kugeln wird die Einheitskugel auf sich selbst abgebildet. Es bildet auch das Innere der Einheitskugel auf sich selbst ab, wobei Punkte außerhalb der orthogonalen Kugel innerhalb und umgekehrt abgebildet werden. Dies definiert die Reflexionen des Poincaré-Scheibenmodells, wenn wir auch die Reflexionen durch die Durchmesser einbeziehen, die die Halbkugeln der Einheitskugel trennen. Diese Reflexionen erzeugen die Gruppe von Isometrien des Modells, die uns sagt, dass die Isometrien konform sind. Daher ist der Winkel zwischen zwei Kurven im Modell der gleiche wie der Winkel zwischen zwei Kurven im hyperbolischen Raum.

Siehe auch[edit]

^ Altshiller-Court (1952, S. 230)
^ Kay (1969, S. 264)
^ ^ein ^b Dutta, Surajit (2014) Eine einfache Eigenschaft von gleichschenkligen Dreiecken mit Anwendungen, Forum Geometricorum 14: 237–240
^ Kay (1969, S. 265)
^ Kay (1969, S. 265)
^ Kay (1969, S. 269)
^ M. Pieri (1911, 12) “Nuovi principia di geometria della inversion”, Giornal di Matematiche di Battaglini 49: 49–96 & 50: 106–140
^ Kasner, E. (1900). “Die invariante Theorie der Inversionsgruppe: Geometrie auf einer quadratischen Oberfläche”. Transaktionen der American Mathematical Society. 1 (4): 430–498. doi:10.1090 / S0002-9947-1900-1500550-1. hdl:2027 / miun.abv0510.0001.001. JSTOR 1986367.
^ Coxeter 1969, S. 77–95
^ AS Smogorzhevsky (1982) Lobatschewskische Geometrie, Mir Publishers, Moskau
^ Joel C. Gibbons und Yushen Luo (2013) Färbungen der n-Kugel und inversive Geometrie

Verweise[edit]

Altshiller-Court, Nathan (1952), College-Geometrie: Eine Einführung in die moderne Geometrie des Dreiecks und des Kreises (2. Aufl.), New York: Barnes & Noble, LCCN 52-13504
Blair, David E. (2000), Inversionstheorie und konformes Mapping, American Mathematical Society, ISBN 0-8218-2636-0
Brannan, David A.; Esplen, Matthew F.; Gray, Jeremy J. (1998), “Kapitel 5: Inversive Geometrie”, Geometrie, Cambridge: Cambridge University Press, S. 199–260, ISBN 0-521-59787-0
Coxeter, HSM (1969) [1961], Einführung in die Geometrie (2. Aufl.), John Wiley & Sons, ISBN 0-471-18283-4
Hartshorne, Robin (2000), “Kapitel 7: Nichteuklidische Geometrie, Abschnitt 37: Zirkuläre Inversion”, Geometrie: Euklid und darüber hinaus, Springer, ISBN 0-387-98650-2
Kay, David C. (1969), Hochschulgeometrie, New York: Holt, Rinehart und Winston, LCCN 69-12075

Externe Links[edit]

after-content-x4

Inversive Geometrie – Wikipedia

Inversion im Kreis [edit]

Umkehrung eines Punktes[edit]

Kompass- und Linealkonstruktion[edit]

Duttas Bau[edit]

Eigenschaften[edit]

Beispiele in zwei Dimensionen[edit]

Anwendung[edit]

Pol und Polar[edit]

In drei Dimensionen[edit]

Beispiele in drei Dimensionen[edit]

Kugel[edit]

Zylinder, Kegel, Torus[edit]

Sphäroid[edit]

Hyperboloid eines Blattes[edit]

Stereographische Projektion als Umkehrung einer Kugel[edit]

6-Kugel-Koordinaten[edit]

Axiomatik und Verallgemeinerung[edit]

Invariant[edit]

Beziehung zum Erlangen-Programm[edit]

Erweiterung[edit]

Gegenbewegung[edit]

Kreise in Kreise verwandeln[edit]

Höhere Geometrie[edit]

In höheren Dimensionen[edit]

Antikonformale Zuordnungseigenschaft[edit]

Inversive Geometrie und hyperbolische Geometrie[edit]

Siehe auch[edit]

Verweise[edit]

Externe Links[edit]

Recent Posts

Recent Comments

Archives

Categories

Meta