Hessesche Normalフォーム-Wikipedia

Posted on June 13, 2023 by lordneo

before-content-x4

ヘッセシュ通常のフォーム 、 ヘッセ通常の形 また ヘッセシュ通常のフォーム 数学の直線またはフラット方程式の特別な形式です。ヘッセッシュの通常の形は、しばしばポイントの距離を直線に与えるのに役立ちます（im

{displaystyle mathbb {r} ^{2}}

after-content-x4

$mathbb {R} ^{2}$ またはレベル（im

{displaystyle mathbb {r} ^{3}}

$mathbb R^3$ ）計算します。ドイツの数学者であるオットー・ヘッセにちなんで名付けられました。

直線方程式のヘッセシュ正常形

{displaystyle {tfrac {1} {sqrt {5}}}、x+{tfrac {2} {sqrt {5}}}、y- {6} {sqrt {5}}}}}}}}

Table of Contents

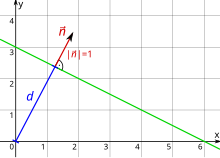
ベクトル形式 [ 編集 | ソーステキストを編集します ]

ヘッセの通常の形では、標準化された通常のベクトルはユークリッドレベルにあります

{displaystyle {vec {n}} _ {0}}

${vec n}_0$ 直線の（通常のユニットベクトル）、およびその距離

after-content-x4

{displaystyle dgeq 0}

$dgeq 0$ 座標起点によって記述されています。直線は、レベル上のそれらのポイント、それらのローカルベクターで構成されています

{displaystyle {vec {x}}}

${vec {x}}$ 方程式

{displaystyle {thing {x}} cdot {thing {n}} _ {0} -d = 0}

満たす。こちらを参照してください

{displaystyledot}

$cdot$ スカラー製品。

通常のベクトルは、ストレートに直交するベクトルですd。 H.それに直角を形成します。

通常のユニットベクトルとして、それは長さでなければなりません

{displaystyle | {vec {n}} _ {0} | = 1}

$|{{vec n}}_{0}|=1$ 彼は座標ジャンプから直線に向かって指している必要があるので、それはしなければなりません

{displaystyle {thing {x}} cdot {thing {n}} _ {0} geq 0}

${vec x}cdot {{vec n}}_{0}geq 0$ 有効です。

ヘッセの通常の形では、直線のポイントは、まっすぐなポイントの局所ベクトルからのスカラー積とゲラデンの通常のベクトルが、原点からの直線の距離に等しいという事実によって暗黙的に定義されます。ローカルベクトルの1つのポイント

{displaystyle {vec {x}}}

${vec {x}}$ 方程式は満たされません

{displayStyle {thing {x}} cdot {thing {n}} _ {0}> d}

${vec x}cdot {{vec n}}_{0}>d”></span>通常のベクトルが表示される直線の側面、その他の側面。座標ジャンプは、たとえ起源のラインではない場合でも、常にネガティブな側面にあります。 </p> <h4><span class=$ 例 [ 編集 | ソーステキストを編集します ]

は

{displaystyle {vec {n}} _ {0} = {begin {pmatrix} 3/5 \ 4/5end {pmatrix}}}}

${displaystyle {vec {n}}_{0}={begin{pmatrix}3/5\4/5end{pmatrix}}}$ ストレートの通常のユニットベクトルと

{displaystyle d = 6/5}

${displaystyle d=6/5}$ 原点からのストレートの距離を使用するので、通常のフォームが得られます

{displaystyle {tfrac {3} {5}}、x+{tfrac {4} {5}}、y- {tfrac {6} {5}} = 0}

の選択

{displaystyle（x、y）}

$(x,y)$ たとえば、この方程式が満たされます

{displaystyle（2.0）}

$(2,0)$ また

{displaystyle（-2,3）}

$(-2,3)$ 、次に、ストレートポイントに対応します。

計算 [ 編集 | ソーステキストを編集します ]

サポートベクトルを備えた直線の通常の形から

{displaystyle {vec {p}}}

${vec {p}}$ および通常のベクトル

{displaystyle {vec {n}}}

${vec {n}}$ ストレートの標準化および署名された通常のベクトル

{Displaystyle {thing {n}} _ {0} = {begin {Cases} {frac {thing {n}} {| {thing {n}} |}} } {| {thing {n}} |}} & {text {Falls}} ~ {thing {p}} cdot {n}} <0nd {Cases}}}

決定。原点から直線の距離は

{displaystyle d = {thing {p}} cdot {thing {n}} _ {0}}}}

決定されます。この距離は、ベクトルの直交投影の長さに対応します

{displaystyle {vec {p}}}

${vec {p}}$ 方向ベクトルを備えた直線

{displaystyle {vec {n}} _ {0}}

${vec n}_0$ 。

他の形式の直線ギア方程式、座標形式、軸セクション形状、パラメーター形状、および2つのポイント改革、関連する通常の形式の直線が最初に決定され（通常の形式の計算を参照）、次に通常の形式が決定されます。

距離計算 [ 編集 | ソーステキストを編集します ]

通常の形のヘッセの助けを借りて、任意のポイントからの距離は

{displaystyle q}

$Q$ ストレートのレベルで

{displaystyle g}

$g$ ローカルベクトルがあるという事実によって単純に計算されます

{displaystyle {vec {q}}}

${vec {q}}$ ポイントの直線で使用されます。

{displaystyle d（q、g）= {vec {q}} cdot {vec {n}} _ {0} -d}

この距離は標識の影響を受けます

{displaystyle d（q、g）> 0}

$d(Q,g)>0″></span>ポイントです <span class=$

{displaystyle q}

$Q$ 通常のベクトルがポイントする直線の側面、そうでなければ反対側。

または、絶対量を使用できます。

{displaystyle d（q、g）= | {vec {q}} cdot {vec {n}} _ {0} -d |}

または、（標準化されていない）通常のベクトルを使用します。

{displaystyle d（q、g）=左| {frac {vec {q}} cdot {vec {n}} – d} {| {vec {n}} |}}右|}}

座標フォーム [ 編集 | ソーステキストを編集します ]

全般的 直線の座標形式です

{displaystyle ax+by+c = 0}

この方程式が分割されている場合

{displaystyle {sqrt {a^{2}+b^{2}}}}

$sqrt{a^2+b^2}$ 、あなたは ヘッセシュ通常のフォーム 座標方程式：

{displaystyle {frac {ax+by+c} {sqrt {a^{2}+b^{2}}} = 0}

特性：

ポイントの距離

{displaystyle（x_ {0}、y_ {0}）}

$(x_{0},y_{0})$ ストレートからです

{displaystyle d（x_ {0}、y_ {0}）=左| {frac {ax_ {0}+by_ {0}+c} {sqrt {a^{2}+b^{2}}}}右| }

{displaystyle {vec {n}} _ {0} = left（{frac {a} {sqrt {a^{2}+b^{2}}}}}}}}、

の直線方程式です 明示的 形状

{displaystyle y = mx+d}

$y=mx+d$ 、そうです

{displaystyle a = m、; b = -1、; c = d}

${displaystyle a=m,;b=-1,;c=d }$ 。方程式を使用したy軸に平行

{displaystyle x = d}

${displaystyle x=d}$ ヘッシュの正常な形があります

{displaystyle x-d = 0}

${displaystyle x-d=0}$ 。

レベル方程式のヘッセシュ正常形

描写 [ 編集 | ソーステキストを編集します ]

同様に、ヘッセシェ通常の形の3次元空間のレベルは、標準化された（おそらくサイン付き）通常のベクトルによって使用されます

{displaystyle {vec {n}} _ {0}}

${vec n}_0$ レベルとその距離

{displaystyle dgeq 0}

$dgeq 0$ 座標起点によって記述されています。 1つのレベルは、部屋のそれらのポイント、その地元のベクトルで構成されています

{displaystyle {vec {x}}}

${vec {x}}$ 方程式

{displaystyle {thing {x}} cdot {thing {n}} _ {0} -d = 0}

満たす。ここの通常のベクトルは、レベルで垂直なベクトルです。通常のベクトルは順番に必要です

{displaystyle | {vec {n}} _ {0} | = 1}

$|{{vec n}}_{0}|=1$ 座標からの独自とポイントはレベルに向かってジャンプするので、

{displaystyle {thing {x}} cdot {thing {n}} _ {0} geq 0}

${vec x}cdot {{vec n}}_{0}geq 0$ 有効です。

ヘッセの通常の形式では、レベルのポイントは、レイヤーポイントの局所ベクトルからのスカラー積とレベルの通常のベクトルが、原点からのレベルの距離に等しいという事実によって暗黙的に定義されます。再び1つのポイントで、そのローカルベクトル

{displaystyle {vec {x}}}

${vec {x}}$ 方程式はレベルで満たされます。適用可能です

{displayStyle {thing {x}} cdot {thing {n}} _ {0}> d}

${{vec x}}cdot {{vec n}}_{0}>d”></span>、次に、ポイントは、通常のベクトルが表示されるレベルの側面、そうでなければ反対側にあります。座標ジャンプは、常にレベルのレベルではない場合、常にレベルのネガティブ側にあります。 </p> <h3><span class=$ 例 [ 編集 | ソーステキストを編集します ]

たとえば、特定のレベルの標準化された通常のベクトルです

{displaystyle {vec {n}} _ {0} = {begin {pmatrix} {tfrac {2} {3} {3}} \ {tfrac {1} {3}} \ – {tfrac {2} {3}} ent {pmatrix}}}}}

${displaystyle {vec {n}}_{0}={begin{pmatrix}{tfrac {2}{3}}\{tfrac {1}{3}}\-{tfrac {2}{3}}end{pmatrix}}}$ 原点からのレベルの距離

{displaystyle d = {tfrac {4} {3}}}

$d={tfrac 43}$ 、したがって、レベル方程式として取得します

{displaystyle {tfrac {2} {3}}、x+{tfrac {1} {3}}、y- {tfrac {2} {3}}、z- {tfrac {4} {3}} = 0}

の選択

{displaystyle（x、y、z）}

$(x,y,z)$ たとえば、この方程式が満たされます

{displaystyle（1,2,0）}

$(1,2,0)$ また

{displaystyle（2、-2、-1）}

$(2,-2,-1)$ 次に、レベルポイントに対応します。

計算 [ 編集 | ソーステキストを編集します ]

サポートベクトルを使用したレベル方程式の通常の形式から

{displaystyle {vec {p}}}

${vec {p}}$ および通常のベクトル

{displaystyle {vec {n}}}

${vec {n}}$ レベルの標準化および署名された通常のベクトルは、2つの次元の場合と同様に実行できます

{Displaystyle {thing {n}} _ {0} = {begin {Cases} {frac {thing {n}} {| {thing {n}} |}} } {| {thing {n}} |}} & {text {Falls}} ~ {thing {p}} cdot {n}} <0nd {Cases}}}

決定。原点からのレベルの距離は

{displaystyle d = {thing {p}} cdot {thing {n}} _ {0}}}}

決定されます。この距離は、ベクトルの直交投影の長さに対応します

{displaystyle {vec {p}}}

${vec {p}}$ 方向ベクトルを備えた直線

{displaystyle {vec {n}} _ {0}}

${vec n}_0$ 。

関連するレベルの通常の形式は、最初にレベル方程式の他の形式、座標形式、軸セクション、パラメーター形状、3つのポイント改革（通常の形の計算を参照）、次に通常の形式から決定されます。

距離 [ 編集 | ソーステキストを編集します ]

通常の形のヘッセの助けを借りて、任意のポイントからの距離は

{displaystyle q}

$Q$ レベルの部屋で

{displaystyle e}

$E$ 再びローカルベクトルであるという事実によって計算されました

{displaystyle {vec {q}}}

${vec {q}}$ ポイントのレベル方程式で使用されます。

{displaystyle d（q、e）= {vec {q}} cdot {vec {n}} _ {0} -d}

この距離は再び拒否されます

{displaystyle d（q、e）> 0}

$d(Q,E)>0″></span>ポイントです <span class=$

{displaystyle q}

$Q$ 通常のベクトルがポイントするレベルの側面、そうでなければ反対側。

距離計算は、距離を使用して通常のフォームの助けを借りてよく使用されますが

{displaystyle d}

$d$ 座標ジャンプの指導は、サポートベクトルを備えた同様のヘッセ正常形態に時々使用されます。 ^[初め]

レベルのヘッセシュ正常形式は次に

{displaystyle ecolon、（{thing {x}} – {thing {p}}）cdot {thing {n}} _ {0} = 0}

したがって

{displaystyle {vec {p}}}

${vec {p}}$ レベルのサポートベクトルです。

スペーサー [ 編集 | ソーステキストを編集します ]

これにより、ローカルベクトルを使用したポイントQの距離式になります

{displaystyle {vec {q}}}

${vec {q}}$ レベルから

{displaystyle e}

$E$ サポートベクトル付き

{displaystyle {vec {p}}}

${vec {p}}$ および通常のユニットベクトル

{displaystyle {vec {n}} _ {0}}

${vec n}_{0}$

{displaystyle d（q、e）= |（{thing {q}} – {thing {p}}）cdot {thing {n}} _ {0} |}}

一般に、ヘッセの通常の形は誇張可能なレベルです

{displaystyle n}

$n$ – 説明されている次元ユークリッド空間。の中に

{displaystyle n}

$n$ – 次元のユークリッドスペースは、ローカルベクターのポイントからそれに応じて構成されています

{displaystyle {vec {x}}}

${vec {x}}$ 方程式

{displaystyle {thing {x}} cdot {thing {n}} _ {0} -d = 0}

満たす。それは一緒です

{displaystyle n}

$n$ 2つまたは3つのコンポーネントベクトルの代わりにコンポーネント。超高レベルが共有します

{displaystyle n}

$n$ – 2つの部分の次元空間。これは、半スペースと呼ばれます。ローカルベクトルの1つのポイント

{displaystyle {vec {x}}}

${vec {x}}$ 満たされた方程式は、まさにハイパーボーンレベルにあります。適用可能です

{displayStyle {thing {x}} cdot {thing {n}} _ {0}> d}

${{vec x}}cdot {{vec n}}_{0}>d”></span>、次に、ポイントは、通常のベクトルが表示されるハーフスペースにあります。 </p> <div class=$

ヘッセシュ通常のフォーム：角度

オットー・ヘッセは1865年に彼の本でリードしました 分析ジオメトリ 一般的なフォームに加えて

{displaystyle ax+by+c = 0}

$ax+by+c=0$ 直線方程式 通常のフォーム

{displaystyle xcos alpha +ycos beta -delta = 0}

a。ある

{displaystyle alpha、beta}

${displaystyle alpha ,beta }$ 座標軸の反対側のゼロポイントを通る通常の角度と

{displaystyledelta}

$delta$ ゼロポイントからの直線の距離。そこには

{displaystyle cos beta = sin alpha}

${displaystyle cos beta =sin alpha }$ あなたは今日書いています

{displaystyle xcos alpha +ysin alpha -delta = 0。}

レベルの通常の形式は同様に説明されています。

ヘッセは、通常のフォームの重要な幾何学的特性を示しています。それを使用すると、ストレートまたはレベルからポイントの距離を簡単に決定できます。

ストレートまたはレベルを説明するこの有利な方法は、後に著者によって引き継がれました。 ヘッセシュ通常のフォーム 専用 ^[2]。

ヘッセの本では、因子を乗算することにより、一般的な形式の通常の形への通常の変換も

{displaystyle {tfrac {1} {sqrt {a^{2}+b^{2}}}}}}

${displaystyle {tfrac {1}{sqrt {a^{2}+b^{2}}}}}$ 含む。

O.ヘッセ：スケールラインの分析ジオメトリからの講義、レベルのポイントと円の円。 E.B. Teubner、1865。
アルフレッド・クリーブシュ、フェルディナンド・リンデマン博士： ジオメトリに関する講義 、Springer-Publiser、1891/2013、ISBN 366315709、978615757700、S。11。
ローサルパピュラ：数学的式コレクション：エンジニアと科学者向け。 Springs、2009、ISBN 978-3-8348-9598-1。
Harald Scheid、Wolfgang Schwarz：線形代数と分析の要素。 Springs、2009、IBN 978-3-8274-2255-2。

↑ アントン・ビガルケ、ノーバート・ケーラー（編）：数学。高校アッパースクールベルリンベーシックコースMA-3 。 Cornelsen Verlag、Berlin 2011、ISBN 978-3-040003-4、 S. 137 。
↑ M. Koecher、A。Krieg： レベル 、Springer-Verlag、2007、ISBN 354049328X、9783540493280、S。114。

after-content-x4

Hessesche Normalフォーム-Wikipedia

ベクトル形式 [ 編集 | ソーステキストを編集します ]

計算 [ 編集 | ソーステキストを編集します ]

距離計算 [ 編集 | ソーステキストを編集します ]

座標フォーム [ 編集 | ソーステキストを編集します ]

描写 [ 編集 | ソーステキストを編集します ]

計算 [ 編集 | ソーステキストを編集します ]

距離 [ 編集 | ソーステキストを編集します ]

スペーサー [ 編集 | ソーステキストを編集します ]

Recent Posts

Recent Comments

Archives

Categories

Meta