Simsonsche Gerade – ウィキペディア

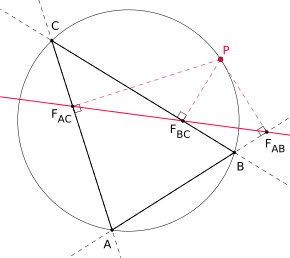
シムソンは今 三角形のジオメトリのオブジェクトです。 1つのポイントのベースポイントです

${displaystyle p}$

三角形の（おそらく拡張された）ページの伐採されたプレートから

${DisplayStyle Triangle ABC}$

一般的なストレートでは、これは シムソンは今 また Wallacesheストレート そしてポイント

${displaystyle p}$

あなたより pol 専用。これはまさに場合です

${displaystyle p}$

の領域

${DisplayStyle Triangle ABC}$

嘘。

シムソンストレートは、数学者のロバートシムソン（1687–1768）にちなんで誤って命名されており、その作業ではシムソンストレートの仕事はありません。実際には、1797年にウィリアムウォレス（1768–1843）によって発見されました。 ^[初め]

シムソンストレートに類似しています [ 編集 | ソーステキストを編集します ]

Simson-Straight間の切断角 [ 編集 | ソーステキストを編集します ]

ハーフエンドとしてのSimson-Straight [ 編集 | ソーステキストを編集します ]

群衆 [ 編集 | ソーステキストを編集します ]

三角筋の接線としてまっすぐにシムソン シムソンポールを離れます ${displaystyle P}$ サークルでハイキングし、その後、シムソンガラデンの結果として生じるゲラデンの群衆は、封筒曲線としてシュタイナーハイポコジロイドとも呼ばれる陰鬱である。 [初め] [2]

その他 [ 編集 | ソーステキストを編集します ]

2つの三角形が同じ領域を持ち、それに関連するシムソンストレートと同じ極である場合、2つのシムソンストレートの切断角は極の選択に依存しません。言い換えれば、すべての点について

${displaystyle p}$

2つの三角形の共通領域には、2つの関連するSimsonストレートの等しい切断角があります。

証明されています：嘘

${displaystyle p}$

の領域

${DisplayStyle Triangle ABC}$

、したがって、ベースポイントは一般的なストレートにあります。
これを行うには、それを示しています

${displaystyle角度EFP+角度PFD = 180^{circ}}$

適用可能です。

ベースポイント

${displaystyle e}$

と

${displaystyle f}$

谷の輪の上に横たわってください

${displaystyle [pa]}$

。周囲（末梢凝固）のサイズは同じ円形のアーチの上に同じサイズであるため、続きます

${displayStyle {begin {aligned} angle efp＆= 90^{circ}+angle efa = 90^{circ}+angle epa \＆= 90^{circ}+（90^{circ} -Angle PAC）= 180^{circ} -Angle Pacend {aligned}}}}$

。

一方、そうです

${displaystyle pbca}$

前提条件の長期的なもの。反対の角度

${displaystyle angle pac}$

と

${displaystyle angle cbp}$

したがって、この広場は互いに補完します

${displaystyle 180^{circ}}$

。全体として、これは

${displaystyle angle efp = angle cbp}$

。

ポイント

${displaystyle d}$

と

${displaystyle f}$

谷の輪の上に横たわってください

${displaystyle [pb]}$

、 そう

${displaystyle pbdf}$

腱への憧れです。以前と同様に、あなたは閉じます

${displaystyle angle pfd = angle dbp}$

。なぜなら

${displaystyle角度dbp+角度cbp = 180^{circ}}$

あなたはそれから得ます

${displaystyle {begin {aligned} angle pfd＆= 90^{circ} -Angle dfb = 90^{circ} – （90^{circ} -Angle pbd）\＆= angle pbd = 180^{circ} -Angle cbpend {aligned}}}}}}$

。

そうです

${displaystyle angle efp+angle pfd = angle cbp+（180^{circ} -Angle CBP）= 180^{circ}}}$

証明された主張。

注：指定された証拠は、スケッチに示されている高度ポイントの位置を指します。これが異なる場合、それに応じて理由を変更する必要があります。

1. ↑ ^{a b c d そうです} H. S. M. Coxeter、S。L。Greitzer： シムソンライン 。 §2.5ジオメトリの再検討。の： 算数。協会。 Amer。、 ワシントンDC 1967、S。41。
2. ↑ ^{a b} エリック・W・ポインターシュタイン： Simson-straight 。 の： Mathworld （英語）。

• マックス・コチャー、アロイの戦争： レベル 。 3.エディション。 Springer-Verlag、Berlin 2007、ISBN 978-3-540-49327-3、pp。170–172。
• H. S. M. Coxeter、S。L。Greitzer： 時代を超越した幾何学 。クレット、シュトゥットガルト1983。
• ロジャー・A・ジョンソン： 高度なユークリッドジオメトリ 。 Dover 2007、ISBN 978-0-486-46237-0、p。137ff。、206 ff。、243、251（1929年にホートンミフリンカンパニー（ボストン）でタイトルの下で出版物 現代の幾何学 ）。
• ロス・ホンズバーガー： 19世紀および20世紀のユークリッド幾何学のエピソード 。国、1995、p。43-48、82-83、121、128–136。