Kuss番号-Wikipedia

Posted on by
before-content-x4

ジオメトリで

n {displaystyle n}
after-content-x4

-the キス （また 連絡先番号 ）の最大数

n {displaystyle n}

– 次元ユニットボール（半径1のボール）。同時に、重複することなくユークリッドスペースの別のそのようなユニットボールに触れることができます。から ゲートキス ボールの中心がグリッドに配置されているときに話す場合。として キス番号の問題 キスの数を計算するための一般的な公式の欠如は知られています。

キスの最初の数は2です。

キスの2番目の数は6です。

n = 1： 次元にはそれがあります スクープ ボールはありませんが、そのエンドポイントは、原点から距離1を持つエンドポイントがあります。ここでは、さらにルートを両方のエンドポイントに追加できるため、次元のKISSの数は明らかに2になります。

n = 2： 2番目の次元にはそれがあります スクープ ボールではなく、半径1の円です。明らかに、できるだけ多くのコインを配置するタスクのこの次元のキスの数を決定する問題に明らかに対応して、それらがすべて同じ中央コインに触れるようにします。 2番目の次元のキスの数が6であることを見るのは簡単です（そして証明する）。

n = 3： 3番目の次元では、キスの数を決定するのはそれほど簡単ではありません。右側のグラフィックを参照してください。 12個のボールをアレンジして、中央のボールに触れるように簡単に配置できます（たとえば、その中心がキューボクターダーの角を形成するように）。しかし、あなたはまだボールの間に多くの空のスペースを見ることができ、13番のボールを追加できるかどうか疑問に思うことができます。この問題は、1692年にケプラーズの推定につながった、アイザック・ニュートンと数学者のデイビッド・グレゴリーとの間の有名な紛争の対象でした。ニュートンは、最大値が12であると主張した、とグレゴリーはそれが13歳だと言った。最初の出版物は19世紀に登場しました、 [初め] [2] [3] ニュートンの主張の証拠を封じ込めたと主張した。今日の基準によれば、正式な証拠は [4] ジョン・リーチによる1956年 [5] 提供された。

after-content-x4

n = 4： 第4次元24のキス番号が証明されたのは、21世紀の初めにのみでした。 [6]

n> 4： さらに、寸法n = 8（240）およびn = 24（196,560）のキスの数が知られています。 24次元空間では、ボールがリーチグリッドのポイントに配置されているため、スペースが残っていません。
1979年の寸法8と24の正確なキス数は、Andrew M. OdlyzkoとNeil J. A. Sloaneによって互いに独立していました [7] またはウラジミール・レヴェンシュテイン [8] 決定。

次の表は、ディメンション24までのキスの数の既知の境界線を再現します。 [9]

キスの3番目の数は12です。
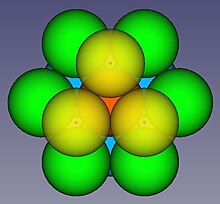
中央のボール（赤）は出身です
同じレベルの6つのボール（緑）、
その上に3つのボール（黄色）と
3つのボール（青、60°が黄色にねじれています）が下に触れました。

キス数の指数関数的な成長。寸法1〜24。灰色の表面は、上下の境界によって制限されます（表を参照）。
寸法のキス番号1…24 [十]
二量体 –
sion 		キス 二量体 –
sion 		キス
低い
国境 		少し
国境 		低い
国境 		少し
国境
初め 2 13 1154 [11] 2069
2 6 14 1606 [11] 3183
3 12番目 15 2564 4866
4 24 16 4320 7355
5 40 44 17 5346 11.072
6 72 78 18 7398 16.572
7 126 134 19 10.688 24,812
8 240 20 17,400 36,764
9 306 364 21 27,720 54.584
十 500 554 22 49.896 82,340
11 582 870 23 93.150 124,416
12番目 840 1.357 24 196,560

推定によると、キス数の成長が指数関数的であることが示されています。テーブルの横にあるグラフィックを参照してください。指数関数的な成長の基礎は不明です。

さらに高次元でのキスの数についてはほとんど知られていない。より低い障壁は、寸法n = 32（276.032）、n = 36（438.872）、n = 40（991.792）、n = 44（2nd948.552）、n = 64（331.737.984）およびn = 80（1,368.532.064）で知られています。 [12番目]

正確な格子数は、寸法1〜9および24で知られています。 [13] [14]
次の表は、グリッドの数または既知の下部の境界線を寸法まで再現します24：

寸法のゲートキス1..24
寸法 グリッド 寸法 グリッド
初め 2 13 ≥918
2 6 14 ≥1422
3 12番目 15 ≥2340
4 24 16 ≥4320
5 40 17 ≥5346
6 72 18 ≥7398
7 126 19 ≥10.668
8 240 20 ≥17,400
9 272 21 ≥27.720
十 ≥336 22 49.896以上
11 ≥438 23 93.150以上
12番目 a ≥756 24 b 196,560

寸法12と24の格子パックには、独自の名前があります。

ボールの半径はオンです

初め / 2 {displaystyle1/2}

標準化され、中央ボールの中心にある座標系の起源は、

n {displaystyle n}

キス 次の不平等のシステムが満たされます。

走る

m {displaystyle m}

と

n {displaystyle n}

から

初め {displaystyle1}

それまで

n {displaystyle n}

と

バツ = （ バツ n ）） n ∈ { 初め … N} {displaystyle x =（x_ {n}）_ {nin {1dots {n}}}}}}}

ベクトルのシーケンスです

n {displaystyle n}

ボールサインポイント、

| | a | | {displaystyle || a ||}

ベクトルの標準（長さ）です

a {displaystyle a}

。 [17] 対称性の理由から、2番目のAllquantorがすべての人にいる場合、それは十分です

m {displaystyle m}

、

n {displaystyle n}

と

m < n {displaystyle m

ストレッチ。
1つ

d {displaystyle d}

– 次元の実際のベクトル空間

r d {displaystyle mathbb {r} ^{d}}

これは、標準の正方形への移行後、マトリックス表記になります

ベクトルはそうです

バツ {displaystyle x}

列ベクトルとして縮小、および

バツ t {displaystyle x^{t}}

対応するラインベクトル（転置マトリックス）、

a t b {displaystyle a^{t}！b}

スカラー製品。この不平等のシステムは、補助変数の形成と導入の後に行われます

と m n {displaystyle y_ {mn}}

[18] 方程式システムで

上記のシステムには合計があります

d de n {displaystyle d！cdot！{n}}

の方程式

n {displaystyle n}

ベクトル

バツ {displaystyle x}

、半分もあります [19] から

n de （ n – 初め ）） {displaystyle n！cdot！（n！ – ！1）}

マトリックス用

と {displaystyle y}

;だから全体的に

d de n + n de （ n – 初め ）） / 2 {displaystyle d！cdot！{n}+n！cdot！（n！ – ！1）/2}

方程式。テストする数の相対サイズのため

n {displaystyle n}

キス 予測可能性の実用的な制限により、ボールはすぐに到達します。

見積り
下限の一般的な形式

n {displaystyle n}

– 次元格子指標はによって与えられます

したがって

z {displaystyle zeta}

Riemannche Zeta関数はです。この境界線は、ミンコフスキー・フローカの判決によって指定されています（ヘルマン・ミンコウスキとエドマンド・フラウカによると）。

  1. ↑ C.ベンダー： 弾丸に等しい最大数の決定。これは、他と同じ半径のボールに置くことができます。 の： アーカイブ数学。物理学。 （Grunert）Volume 56、1874、pp。302–306。
  2. ↑ S.Günther： 立体測定の問題。 の： アーカイブ数学。物理学。 バンド57、1875、S。209–215。
  3. ↑ R.ジャンプ： 編集の発言。 の： アーカイブ数学。物理学。 （Grunert）Volume 56、1874、pp。307–312
  4. ↑ Schütte、van der Waerden： 13ボールの問題。 の： 算数。アナレン。 バンド125、1953、S。325–334。
  5. ↑ リーチ： 13個の球体の問題。 の： 数学的な官報。 バンド40、1956、S。22–23
  6. ↑ オレグ・R・ミューン： 4次元のキス番号 。の： 数学の年代記 。 Vol。 168、 いいえ。 初め 、2008年、 S. 1–32 、arxiv： Math/0309430 。
  7. ↑ Andrew M. Odlyzko、Neil J. A. Sloane： n寸法の単位球体に触れることができるユニット球の数の新しい境界。 の： J.コンビン。仮説。 見る。 A、バンド26、1979、nr。 2、pp。210–214
  8. ↑ ウラジミールI. levenshtein： n次元ユークリッド空間のパッケージの境界について s nr。 6、dokl。アカド。 Nauk SSSR 245 1979。S.1299–1303
  9. ↑ ハンス・D・ミッテルマン、フランク・ヴァレンティン： Kissing Numbersの高精度セミデフィナイトプログラミング境界 。 arxiv： 0902.1105
  10. ↑ 結果 A001116 OEISで
  11. ↑ a b https://www.wolframalpha.com/input/?i=kissingnumber Zinov’evとEricsonの証拠
  12. ↑ Yves Edel、E。M。Rains、N。J。A. Sloane： 寸法32から128のキス数 。の： Combinatoricsの電子ジャーナル。 バンド5、1998年の重さ
  13. ↑ ジョン・ホートン・コンウェイ、ニール・J・A・スローン： キス番号の問題。 と キス番号の境界。 In：John Horton Conway、Neil J. A. Sloane： 球体パッキング、格子、およびグループ。 第2版​​。 Springer-Verlag、ニューヨーク1993。pp。21–24および337–339、ISBN 0-387-98585-9。
  14. ↑ ニールJ. A.スローン、ガブリエレ天国： 現在知られている最高のキス番号のテーブル。
  15. ↑ エリック・W・ポインターシュタイン： Coxeter-Toddlets 。 の： Mathworld （英語）。
  16. ↑ エリック・W・ポインターシュタイン： リーチグリッド 。 の： Mathworld （英語）。
  17. ↑ Sergei Kucherenko et al。： キス番号の問題のための新しい定式化 In：Displete Applied Mathematics、Volume 155、Issue 14、2007年9月1日、1837〜1841ページ、 2：10.1016/j.dam.2006.05.012 。著者は、1つの標準化された球状半径で動作します。
  18. ↑ d。 H.補助マトリックス
  19. ↑ 対称性のため
  20. ↑ エリック・W・ポインターシュタイン： Minkowski-hlawka定理 。 の： Mathworld （英語）。
after-content-x4