
物理学とジオメトリ間の関係は、レバレッジ法の方程式を提供します。その後、質量の比率は

ルートの比率に等しくなります

焦点の位置を説明しています。
バリア中心座座 (また 均質な核心座標 )線形代数およびジオメトリでは、特定のルート、特定の三角形、特定の四面体、またはより一般的には特定のシンプレックスに関連するポイントの位置を説明するのに役立ちます。
ポイントのレベルの核心座標
 あなたは3つの質量の状況になることができます
あなたは3つの質量の状況になることができます
 与えられた三角形の角にあるそれを紹介し、それらの焦点
与えられた三角形の角にあるそれを紹介し、それらの焦点
 IS(写真を参照)。それは条件にのみ依存するので、あなたは書きます
IS(写真を参照)。それは条件にのみ依存するので、あなたは書きます
 。すべての質量が同じ場合、そうです
。すべての質量が同じ場合、そうです
 三角形の幾何学的な焦点と、口径の座標があります
三角形の幾何学的な焦点と、口径の座標があります
 。口径の座標は、次の特性を通じて幾何学的な意味を受け取ります。1次元では、質量比は部分的な距離の比率(2番目の画像を参照)であり、2次元では、質量条件は部分的な三角形の表面条件です。
。口径の座標は、次の特性を通じて幾何学的な意味を受け取ります。1次元では、質量比は部分的な距離の比率(2番目の画像を参照)であり、2次元では、質量条件は部分的な三角形の表面条件です。
1827年にA. F.Möbiusによる彼の著書で初めてのバリゼン集座 Barechnurch Calcul 紹介された。 [初め] [2] それらは均一な座標の特別なケースです。通常の均質な座標に大きな違いがあります。 B.レベルでは、方程式を通るリモートストレートの説明は
 それ以外の
それ以外の
 。
。
三線の座標に加えて、バリーセンター座標は三角形のジオメトリに重要な役割を果たします。 CEVAの判決など、ルートの条件が関係している場合はどこでも、適切なツールです。しかし、ジオメトリだけでなく、コンピューター支援設計の領域でも、三角形のベジエ表面を生成するために使用されます。 [3] [4]
意味 [ 編集 | ソーステキストを編集します ]
なれ
 コーナーのローカルベクター
コーナーのローカルベクター
 アフィンルームの1つのシンプルです
アフィンルームの1つのシンプルです
 。アフィンスペースには次元があります
。アフィンスペースには次元があります
 。ポイントの場合
。ポイントの場合
 の
の
 支払い
支払い
 その合計はゼロではなく、方程式を与えます
その合計はゼロではなく、方程式を与えます
- (g)

充実した、と言います
 それは バリア中心座座 ポイント
それは バリア中心座座 ポイント
 ポイントに関して
ポイントに関して
 と書いています
と書いています
 。明らかに角に適用されます
。明らかに角に適用されます
-
 。
。
バリア中心の座標は明確ではありません:それぞれのためです
 また、多くのゼロについて説明します
また、多くのゼロについて説明します
 ポイント
ポイント
 。言い換えれば、座標の条件のみが不可欠です。スペルはこのプロパティにある必要があります
。言い換えれば、座標の条件のみが不可欠です。スペルはこのプロパティにある必要があります
 覚えて。 Bary Centered Coordinatesは、の均一な座標として使用できます
覚えて。 Bary Centered Coordinatesは、の均一な座標として使用できます
 – 次元射影空間
– 次元射影空間
 アフィンルームから取り出します
アフィンルームから取り出します
 部分はです。のポイントです
部分はです。のポイントです
 のポイント
のポイント
 、 いいえ 方程式で
、 いいえ 方程式で
 特定のハイパーベール(リモートハイパーテイクレベル)です。
特定のハイパーベール(リモートハイパーテイクレベル)です。
方程式 (g) 通常の形にある方程式の均一な線形システムです
- (g ‘)

かきましょう。
座標に会います
 加えて 標準化条件
加えて 標準化条件
- (n)

だから人は話します 標準化された核心座標。 この場合、数字はです
 明らかに 決定(以下を参照)とできます
明らかに 決定(以下を参照)とできます
 (元のまっすぐ)アフィンポイントとしても
(元のまっすぐ)アフィンポイントとしても
 Hypereneath Desk
Hypereneath Desk
 方程式で
方程式で
 取った。
取った。
標準化を正式に確保するために、できます (n) 座標の後に溶解し、n-tupelに挿入します。 zを解く場合。 B.後
 オン、結果
オン、結果
 。
。
知らせ :用語は均一に使用されません。多くの著者は、標準化条件が満たされている場合にのみ、バリー中心の座標について語っています。
標準化されたバリセントリック座標は、各個々のバリーセンター座標を座標の合計で除算することで簡単に決定できます。
特性 [ 編集 | ソーステキストを編集します ]
シンプレックスのポイント [ 編集 | ソーステキストを編集します ]
座標が正の場合、ポイントはです
 の凸シェルで
の凸シェルで
 、これらの礎石を備えたシンプレックスで。シンプレックスの礎石の合計としての凸シェル内の点の表現は アフィンの組み合わせ また バリーセンターの組み合わせ 呼び出されました。
、これらの礎石を備えたシンプレックスで。シンプレックスの礎石の合計としての凸シェル内の点の表現は アフィンの組み合わせ また バリーセンターの組み合わせ 呼び出されました。
マスセンター [ 編集 | ソーステキストを編集します ]
切り替えから抜け出す方法
- (s)

定義方程式 (g) 見て、できます
 大衆の配置の大衆の中心(バリーセンター)として
大衆の配置の大衆の中心(バリーセンター)として
 礎石で
礎石で
 シンプレックスを取ります。これが用語の起源です バリーセンター。
シンプレックスを取ります。これが用語の起源です バリーセンター。
の物理的意味
- 方程式 (g) :焦点の総質量
 ゼロポイントで個々の質量と同じトルクを引き起こし、
ゼロポイントで個々の質量と同じトルクを引き起こし、
- 方程式 (g ‘) :個々の大衆によって生成されたトルクの合計が焦点を合わせています
 0に等しい。
0に等しい。
2つのポイントの中心 [ 編集 | ソーステキストを編集します ]
それは
 標準化 (!)2つのポイントのバリーセンター表現
標準化 (!)2つのポイントのバリーセンター表現
 、次にセンター
、次にセンター
 バリーセンターの表現
バリーセンターの表現
-

存在、明確に標準化された座標 [ 編集 | ソーステキストを編集します ]
標準化された核心座標が明確に決定されます。なぜなら、あなたはそれを試してみるからです (g ‘) と (n) 1つの因子(n = 3)を除き、三角形の配向表面であり、3次元の場合(n = 4)四面体の配向容量であるため、Cramerルールの助けを借りて、式の反発性線形系は、分母の決定要因ではありません。
状態を離れる場合 (n) 再び落ちると、線形均一なシステムがあります (g ‘) 1次元ソリューション(上記の射影領域のポイント
 )。大きい場合
)。大きい場合
 適用されます。
適用されます。
ゼロポイントとスケーリングからの独立 [ 編集 | ソーステキストを編集します ]
バリセントリックな座標は、アフィン空間のランダムに選択されたゼロポイントからのものではないこと
 去ると、ベクターのシフトが
去ると、ベクターのシフトが
 固定ベクトルへ
固定ベクトルへ
 定義方程式 (g) 変わらないままにします。同じことが均一なスケーリングにも当てはまります(固定係数を不均一に伴うベクターの乗算)。
定義方程式 (g) 変わらないままにします。同じことが均一なスケーリングにも当てはまります(固定係数を不均一に伴うベクターの乗算)。
例 [ 編集 | ソーステキストを編集します ]
レベルでは、シンプレックスは3ポイント(三角形)で構成されています。 H.そうです
 そして、各ポイントには3つのバリア中心の座標があります。
そして、各ポイントには3つのバリア中心の座標があります。
 。たとえば、三角形の幾何学的焦点にはバリーセンターの表現があります
。たとえば、三角形の幾何学的焦点にはバリーセンターの表現があります
 、 その理由は
、 その理由は
 標準化された表現はです
標準化された表現はです

有利不利 [ 編集 | ソーステキストを編集します ]
例でわかるように、必須ポイントを使用できます。 B.均一かつ簡単に説明してください。計算の場合、特定の三角形の特別な(アフィン)座標を考慮に入れる必要はありません。次のセクションでは、アフィン座標をバリゼ集座標に変換する方法を示しています。ただし、バリゼ中心の座標の特定の不利な点は次のとおりです。それらは明確ではなく(非標準化されていない場合)、アフィン座標よりも常に1つの座標があります。
他の均一な座標との違い:例n = 3 [ 編集 | ソーステキストを編集します ]
通常、均質な座標が導入されているため、リモートは座標レベルを通過します。 B.スルー
 説明されています。これには、関連するアフィンレベル(長い距離のポイントなしの射影レベル)を説明するアフィン座標への単純な接続が存在するという利点があります。
説明されています。これには、関連するアフィンレベル(長い距離のポイントなしの射影レベル)を説明するアフィン座標への単純な接続が存在するという利点があります。
 。ただし、座標軸に属する射影点が
。ただし、座標軸に属する射影点が
 アフィンポイントではありません。ポイントだけ
アフィンポイントではありません。ポイントだけ
 アフィンポイントになります。バリゼ中心の座標は、アフィン座標とそのような簡単な関係はありません。このため、座標軸に対応するすべての射影点は
アフィンポイントになります。バリゼ中心の座標は、アフィン座標とそのような簡単な関係はありません。このため、座標軸に対応するすべての射影点は
 アフィン領域では、長い距離ストレートは方程式を通過するため
アフィン領域では、長い距離ストレートは方程式を通過するため
 説明された。
説明された。
焦点
 2つの質量
2つの質量
 上のもの
上のもの
 – 場所の軸
– 場所の軸
 配置されている、場所はそうです
配置されている、場所はそうです
 、レバレッジ法( パワー×パワーアーム=負荷×ロードアーム 、2番目の写真を参照)が満たされています。より正確には:トルクの合計がゼロの場合 [5] そしてそれで:
、レバレッジ法( パワー×パワーアーム=負荷×ロードアーム 、2番目の写真を参照)が満たされています。より正確には:トルクの合計がゼロの場合 [5] そしてそれで:
- (g’2)

この方程式は同等です(セクションを参照してください 意味 ))
- (G2)

解決
 結果:
結果:
- (S2)

負の質量を許可する場合、例えばB.
 、これが結果です (G2) ために
、これが結果です (G2) ために
 総質量
総質量
 と
と
 。
。
の解決策 (g’2) は
 。すべてのソリューションはそれらの複数です。したがって、焦点はバリーセンターの表現にあります(セクションを参照してください 意味 ))
。すべてのソリューションはそれらの複数です。したがって、焦点はバリーセンターの表現にあります(セクションを参照してください 意味 ))

経路の比率としてのバリゼ中心の座標
- (B2)

ある


直線(下)のバリー中心座標。ルートの中心

バリー中心の座標があります

バリーセンターのこの単純な接続とセクションの状況との接続は、三角形の幾何学におけるそれらの重要性の理由です。
声明 (B2) それは 教育率 §21、p。25、Möbiusの本。
標準化 バリア中心の座標もそうでなければなりません (g’2) 状態
- (N2)

満たす。方程式で構成される方程式の不均一なシステムを解く場合 (g’2) 、 (N2) Cramerルールの助けを借りて、標準化された表現の結果
- (NB2)

例: 中間点
 ポイント
ポイント
 Bary Center座標があります
Bary Center座標があります
 標準化された表現で
標準化された表現で

座標の変換 [ 編集 | ソーステキストを編集します ]
三角形の角にあります
 3つの質量
3つの質量
 配置されていると、座標軸の周りのトルクの平衡方程式は
配置されていると、座標軸の周りのトルクの平衡方程式は
- (G’3)

または形式で(参照してください 意味 ))
- (G3)

焦点は座標にあります
- (S3)

特定のポイントのバリー中心座標
 、未定の均一なシステムを緩めることで得ます (G’3) 後
、未定の均一なシステムを緩めることで得ます (G’3) 後
 。標準化方程式を取る場合
。標準化方程式を取る場合
-
- (N3)

- さらに、現在の不均一なLGSは明確であり、Cramerルールの助けを借りて解決できます。結果:


-
- (NB3)

- 一般的な分母は、三角形の二重領域、つまり不均一にゼロです。
- なぜなら
 3つの休憩のうち2つを計算するだけで十分です。
3つの休憩のうち2つを計算するだけで十分です。
- すべてのポイントをとして使用できます
 – ターミナントライティング。標準化なしで行う場合、共通の分母はバリゼ集座標で省略できます。
– ターミナントライティング。標準化なしで行う場合、共通の分母はバリゼ集座標で省略できます。
- (B3)

- すべての決定要因を掛けた場合
 、方向のある領域が作成されます
、方向のある領域が作成されます
 部分三角形
部分三角形
 、
、
 、
、
 (次のセクションも参照してください 三線座標との関係 )。これが適用されます:
(次のセクションも参照してください 三線座標との関係 )。これが適用されます:
- (BF3)

声明 (BF3) それは 教育率 §23、p。26、Möbiusの本。
特別なケース:トライアングルの座標:
特別な右のアングルトライアングルの場合
 参照の三角形にはポイントがあります
参照の三角形にはポイントがあります
 シンプルなバリーセンター座標
シンプルなバリーセンター座標
 。
。
ストレート、交差点、平行性 [ 編集 | ソーステキストを編集します ]

ポイントで

大衆です

。
紫色の類似点には、指定された方程式があります。あなたの一般的な長距離ポイントには座標があります

ラスターポイントの座標は標準化されています。
-
 。
。
-

-

-

- 持っている 一緒にポイント、 もしも
 。
。
- 2つの直線
 それは 平行、 長い距離をまっすぐに切った場合、i。 h。、if
それは 平行、 長い距離をまっすぐに切った場合、i。 h。、if
 。
。
- 3つのポイント
 、
、
 と
と
 まっすぐなときに正確に横たわってください
まっすぐなときに正確に横たわってください

- これにより、方程式が得られます
 指定された2つのポイントの1つ
指定された2つのポイントの1つ
 DeCionAntenFormで:
DeCionAntenFormで:

三線座標との関係 [ 編集 | ソーステキストを編集します ]

部分的な三角形の基本的な側面と高さ
表面用
 部分的な三角形 (BF3) 適用可能です
部分的な三角形 (BF3) 適用可能です
 、それによって
、それによって
 基本(三角形のページ)と部分三角形の高さは(写真を参照)です。適用されます
基本(三角形のページ)と部分三角形の高さは(写真を参照)です。適用されます
- (BT3)

関係 (BT3) バリーセンター座標と三線座標の単純な接続を示しています
 ポイントの。正女の三角形の場合、バリーセンターと三線座標は同じです。長い距離ストレートには、バリゼ中心の座標の方程式があります
ポイントの。正女の三角形の場合、バリーセンターと三線座標は同じです。長い距離ストレートには、バリゼ中心の座標の方程式があります
 。三線座標では、方程式はまだ辺の長さからです
。三線座標では、方程式はまだ辺の長さからです
 三角形の:
三角形の:

特別なポイント、オイラーガレード [ 編集 | ソーステキストを編集します ]
- 幾何学的なフォーカス
 すべての大衆が同じ場合、幾何学的な焦点です。したがって、彼のバリーセンターリング座標はそうです
すべての大衆が同じ場合、幾何学的な焦点です。したがって、彼のバリーセンターリング座標はそうです
 なぜなら (BF3) と
なぜなら (BF3) と
 適用可能です
適用可能です
-
 と
と

(幾何学的焦点も参照してください。)
- ストレートのパラメータープレゼンテーション
1つだけ2つのポイントを介して
 ポイントを用意しています
ポイントを用意しています
 表現
表現
-


コーナーの反対側の側面のポイントの投影
- 片側に投影します
ポイントを投影します
 角から
角から
 反対側から(これは現在方程式です
反対側から(これは現在方程式です
 )、だからあなたはポイントを得る
)、だからあなたはポイントを得る
 (画像を参照)。の座標です
(画像を参照)。の座標です
 標準化 、スプリット
標準化 、スプリット
 距離
距離
 に関して
に関して
 。
。
zです。 B.幾何学的焦点のポイント
 、それで彼は側の真ん中になります
、それで彼は側の真ん中になります
 ルートを投影して共有します
ルートを投影して共有します
 に関して
に関して
 。
。
同じことが他のコーナーからの投影にも当てはまります。
- サークルセンター、着信センターポイント

回路の中心と中心の中心へ:
三角形の面積含有量

と

さまざまな兆候があります
三角形の地区には適用されます
 (inkreisradius)、したがって(参照してください。 (BT3) )回路の中心には、核心座標があります
(inkreisradius)、したがって(参照してください。 (BT3) )回路の中心には、核心座標があります
 そして、
そして、
 適用可能です
適用可能です
 副鼻腔セットの助けを借りて、角度を持つ表現も回路中心の結果として生じます。
副鼻腔セットの助けを借りて、角度を持つ表現も回路中心の結果として生じます。
-

したがって
 角度
角度
 は。
は。
Shopput コーナー
 (真っ直ぐ
(真っ直ぐ
 )方程式があります
)方程式があります
-

彼女は側を切ります
 (方程式
(方程式
 )ポイントで
)ポイントで
 。 (
。 (
 投影としても可能です
投影としても可能です
 側面上
側面上
 閲覧されます。) (B2) 該当する:
閲覧されます。) (B2) 該当する:
-
 他の角度に類似しています。
他の角度に類似しています。
これは三角形の角度の角です
 。
。
三角表面は方向付けられているため、缶です
 そしてそれもそれで
そしてそれもそれで
 負の値を受け入れるかどうか
負の値を受け入れるかどうか
 の同じ側に
の同じ側に
 三角形の側面が角のようにあるのを聞いてください
三角形の側面が角のようにあるのを聞いてください
 か否か。円形の中心点でみんな
か否か。円形の中心点でみんな
 同じサイン。センターセンターの場合、すべての距離には(回路ポイントと同様に)ヒント半径の長さがありますが、距離の1つには他の2つの異なる標識の1つがあります。これにより、入ってくるセンターポイントのバリーセンター表現が得られます。
同じサイン。センターセンターの場合、すべての距離には(回路ポイントと同様に)ヒント半径の長さがありますが、距離の1つには他の2つの異なる標識の1つがあります。これにより、入ってくるセンターポイントのバリーセンター表現が得られます。
-

回路半径と同様に、円の半径があります。
-

- ネイルポイント
三角形のメモのタッチポイントの場所の説明から、バリーセンターの表現を見ることができます。
-

-

-

 明らかにポイントの投影(上記を参照)です
明らかにポイントの投影(上記を参照)です
-

角から
 反対側から。つまり:
反対側から。つまり:
- 3つのストレート
 ポイントをカットします
ポイントをカットします
 、に ネイルポイント 。
、に ネイルポイント 。
ダイマトリックス
-

幾何学的焦点の中心的拡張について説明します(バリゼ中心の座標)
 要因で
要因で
 (セクションSteiner-Ellipse、Steiner-Inllipseを参照)。あなたが形成します
(セクションSteiner-Ellipse、Steiner-Inllipseを参照)。あなたが形成します
 これにより、回路の中心を取得します
これにより、回路の中心を取得します
 。これは:
。これは:
- ポイント
 まっすぐに横になります
まっすぐに横になります
 と
と
 ルートを共有します
ルートを共有します
 2:1の比率。
2:1の比率。
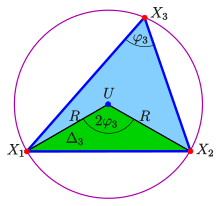
回路ポイント

- 回路ポイント
エリアの中心
 コーナーまで同じ距離があります
コーナーまで同じ距離があります
 、半径。角度
、半径。角度
 部分三角形で
部分三角形で
 円形の角度が設定されているため、角度の2倍の大きさです
円形の角度が設定されているため、角度の2倍の大きさです
 で
で
 。だからエリアはそうです
。だからエリアはそうです
 。同じことが当てはまります
。同じことが当てはまります
 。これは、センタリングポイントのバリーセンター座標が
。これは、センタリングポイントのバリーセンター座標が
-

out
 そして、3つの角度のコジナーは、角度のない表現につながります
そして、3つの角度のコジナーは、角度のない表現につながります
-

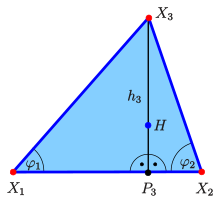
高さの切断点

- 高さの切断点
は
 高さのカットポイント、そうです
高さのカットポイント、そうです
 高さのベースポイント
高さのベースポイント
 (写真を参照)、適用されます
(写真を参照)、適用されます
 なぜなら (B2) は
なぜなら (B2) は
 同様に、他の状況が発生します。これは、高さ-CUTポイントにバリーセンターの座標があることを意味します
同様に、他の状況が発生します。これは、高さ-CUTポイントにバリーセンターの座標があることを意味します
-

角度の場合
 そうです。 B.
そうです。 B.
 、そうです
、そうです
 。
。
- Spieker Point

三角形のスピーカーポイント
あなたがそれらを取るなら ページ
 三角形
三角形
 質量と均等に、関連するエッジフォーカスはSpieker Pointと呼ばれます。 (三角形のトウモロコシと面積の焦点は同一です:側面の側面の交差点。)ページの質量が焦点を合わせていると思うなら、中心
質量と均等に、関連するエッジフォーカスはSpieker Pointと呼ばれます。 (三角形のトウモロコシと面積の焦点は同一です:側面の側面の交差点。)ページの質量が焦点を合わせていると思うなら、中心
 集中して、Spieker Pointはそうです
集中して、Spieker Pointはそうです
 三角形の焦点
三角形の焦点
 サイドの長さで
サイドの長さで
 角の大量割り当てとして。 out
角の大量割り当てとして。 out
 と (S3) フォロー:
と (S3) フォロー:
-

-

Y座標は同様に結果をもたらします。
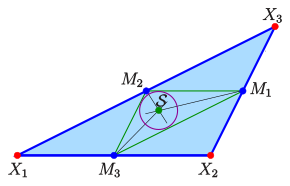
三角形の地区の中心としてのスピーカーポイント

このことから、Spieker Pointのバリア中心の座標を認識できます。
-

の意味
 三角形の場合
三角形の場合
 :
:
上記の考慮事項から(質量
 ポイントで
ポイントで
 )のバリーセンターの表現に従います
)のバリーセンターの表現に従います
 (緑の)三角形について
(緑の)三角形について
 :
:
-

と
 ポイントの長さ
ポイントの長さ
 反対側(緑)側です
反対側(緑)側です
 回路の中心=三角形の角度の交差点
回路の中心=三角形の角度の交差点
 (上記を参照)。このプロパティは、ポイントの可能性を提供します
(上記を参照)。このプロパティは、ポイントの可能性を提供します
 図面を決定する。
図面を決定する。
- ourerized

三角形のオイラーライン
幾何学的焦点
 、センター
、センター
 そして高さの切断点
そして高さの切断点
 フクロウの直線に横たわってください。なぜなら、あなたはポイントでリードしているからです
フクロウの直線に横たわってください。なぜなら、あなたはポイントでリードしているからです
 拡張係数を備えた中央拡張
拡張係数を備えた中央拡張
 スルー、各コーナーは反対側の側面の中央に表示されます(
スルー、各コーナーは反対側の側面の中央に表示されます(
 ページの各側が2:1の比率で分割され、高さが中間クラウンに表示されている場合。だから行きなさい
ページの各側が2:1の比率で分割され、高さが中間クラウンに表示されている場合。だから行きなさい
 の
の
 オーバーで、両方のポイントが共通のまっすぐに横たわっています
オーバーで、両方のポイントが共通のまっすぐに横たわっています
 。周辺地域は、サイドマージン、Feuerbach地区を通って円に入ります。
。周辺地域は、サイドマージン、Feuerbach地区を通って円に入ります。
 )したがって、フクロウストレートにもあります。
)したがって、フクロウストレートにもあります。
バリーセンター座標のフクロウストレートの方程式(上記を参照)
-

-

またはドットを使用します
 :
:
-

等側 トライアングルにはフクロウストレートがありません
 は。
は。
その三角形です 等球 、ただし正直ではありません。 B.
 、したがって、オイラーガレードには方程式があります
、したがって、オイラーガレードには方程式があります
 サイトの側面と同じです
サイトの側面と同じです
 。次に、回路の中心も含まれます。
。次に、回路の中心も含まれます。
その三角形です 右 – 角 、z。 B.
 、そうです
、そうです
 そして、オイラーガレードには方程式があります
そして、オイラーガレードには方程式があります
 そして、ハイポテノーゼの側面の側面です。
そして、ハイポテノーゼの側面の側面です。
CEVAからセット [ 編集 | ソーステキストを編集します ]
- CEVAからセット
Pは三角形内のポイントです
 と
と
 ストレートの交点
ストレートの交点
 側面で
側面で
 (写真を参照)、適用されます
(写真を参照)、適用されます
-

- 証拠
バリア中心の座標のポイントで:
-

-

は
 (ご参照ください 特別なポイント )。 out B2 あなたは得ます
(ご参照ください 特別なポイント )。 out B2 あなたは得ます
 また、ポイントに対するこれらの考慮事項をリードする場合
また、ポイントに対するこれらの考慮事項をリードする場合
 スルー、結果
スルー、結果
-

Steiner-Ellipse、Steiner-Inellipse [ 編集 | ソーステキストを編集します ]
(任意の)三角形の角を通る明確に決定された楕円
 幾何学的焦点の焦点
幾何学的焦点の焦点
 Steiner-Ellipseと呼ばれます。バリゼ中心の座標では、方程式によって行われます
Steiner-Ellipseと呼ばれます。バリゼ中心の座標では、方程式によって行われます
- (se)

説明された。
6ポイントを確認するのは簡単です
-

-

方程式 (se) 充実し、焦点を当てます
 センター(セクションを参照してください 意味 )カップル
センター(セクションを参照してください 意味 )カップル
 は。方程式 (se) だから、コーンの外ではない必要があります
は。方程式 (se) だから、コーンの外ではない必要があります
 (楕円またはハイパーベルまたは放物線)説明。式から
(楕円またはハイパーベルまたは放物線)説明。式から
-
 矛盾
矛盾
-

-

-

次のとおりです
 長い距離ストレートと共通点はありません。 H.
長い距離ストレートと共通点はありません。 H.
 楕円です。
楕円です。
ポイントでの反射
 六角形を残します
六角形を残します
 そして、それによって楕円の不変(楕円は5つのポイントによって明確に決定されます)。したがって、対称ポイントはそうです
そして、それによって楕円の不変(楕円は5つのポイントによって明確に決定されます)。したがって、対称ポイントはそうです
 楕円の中心。
楕円の中心。
センター以来
 腱
腱
 直径
直径
 嘘、接線
嘘、接線
 と並行して
と並行して
 be(楕円を参照)。
be(楕円を参照)。
彼女には方程式があります
 。中央を通って接線に平行にカットします
。中央を通って接線に平行にカットします
 (彼女には方程式があります
(彼女には方程式があります
 )楕円で (se) あなたも2つを手に入れます
)楕円で (se) あなたも2つを手に入れます
 共役点(Steiner-Ellipseを参照)
共役点(Steiner-Ellipseを参照)
-

同じことが他のコーナーの接線にも当てはまります。

Steiner-Inllipse(緑)
中央の拡張機能でシュタイナーエリプスを形成します
 彼らの中心で
彼らの中心で
 要因とともに
要因とともに
 そのため、同じセンターで楕円を取得します
そのため、同じセンターで楕円を取得します
 それは彼らの中央の三角形に触れます。これは、三角形のシュタイナーインリプスです。なぜなら
それは彼らの中央の三角形に触れます。これは、三角形のシュタイナーインリプスです。なぜなら
 の画像マトリックスです
の画像マトリックスです

-

方程式を変換します (se) このマトリックスを備えたシュタイナーエリプスは、バリーセンター座標のシュタイナーインリプスの方程式になります。
- (彼女)


(均一な)バリゼ中心の座標およびレベルの円として標準化されたバリゼ中心座標のコーンとしてのシュタイナー –

- 3D表現
1)方程式を介して (se) 定義されたQuadrik
 の中に
の中に
 (いつものように) オルソゴナレン 座標軸は、座標軸とストレートを含む先端としてゼロポイントを持つまっすぐな円形コーンです
(いつものように) オルソゴナレン 座標軸は、座標軸とストレートを含む先端としてゼロポイントを持つまっすぐな円形コーンです
 軸としてあります。なぜなら、レベルの交差曲線のため
軸としてあります。なぜなら、レベルの交差曲線のため
 方程式のクワドリ (se) 適用可能です
方程式のクワドリ (se) 適用可能です
-

-

-

これは、交差点曲線がユニットボールの平らなカットであり、したがって円(写真の紫色)であることを意味します。
2)方程式のアナログ考慮事項 (彼女) 定義されたQuadrik
 見せる:
見せる:
 また、ゼロポイントが先端とストレートを持つまっすぐな円形コーンでもあります
また、ゼロポイントが先端とストレートを持つまっすぐな円形コーンでもあります
 軸として。ベースサークルはレベルのカットです
軸として。ベースサークルはレベルのカットです
 小さなボールで
小さなボールで
 (写真の緑)。コーンを切ります
(写真の緑)。コーンを切ります
 座標レベルで
座標レベルで
 、起源をまっすぐにします
、起源をまっすぐにします
 、d。 H.コーンは座標レベルに触れます。これは、他のレベルの座標にも適用されます。
、d。 H.コーンは座標レベルに触れます。これは、他のレベルの座標にも適用されます。
3)in 標準化 鋭心性座標(つまり、平野で
 )与えられた三角形が表示されます 等側 そして、シュタイナーエリップスはそれらのものです 回路と回路 。
)与えられた三角形が表示されます 等側 そして、シュタイナーエリップスはそれらのものです 回路と回路 。
4)設定 正統派はありません の座標
 先に、次のもののみが適用されます。コーンは楕円形で、三角形は一般的で、円は楕円です。インコと接触関係が保存されます。
先に、次のもののみが適用されます。コーンは楕円形で、三角形は一般的で、円は楕円です。インコと接触関係が保存されます。
5)と同じように選択します バリーセンターではありません 均一な座標は、元のレベルであります
 長い距離としてまっすぐになり、セット
長い距離としてまっすぐになり、セット
 、これが方程式の説明方法です (se) アフィンエリア(
、これが方程式の説明方法です (se) アフィンエリア(
 )ハイパーベルをダイ
)ハイパーベルをダイ
 。この場合、ポイントは次のとおりです
。この場合、ポイントは次のとおりです
 シダは、漸近線の長い距離ポイントをポイントします。の中に
シダは、漸近線の長い距離ポイントをポイントします。の中に
 あなたは詐欺の交差点としてハイパーベルになれますか
あなたは詐欺の交差点としてハイパーベルになれますか
 レベルで
レベルで
 導入。
導入。
6)参照:inellipse。
計算とプロパティ [ 編集 | ソーステキストを編集します ]
3次元空間では、シンプレックスは角のある四面体です
 。ポイントのバリーセンター座標に
。ポイントのバリーセンター座標に
 2次元の場合(三角形)、均一な線形方程式システムに類似した、与えられた四面体の決定(セクションを参照 意味 ))
2次元の場合(三角形)、均一な線形方程式システムに類似した、与えられた四面体の決定(セクションを参照 意味 ))
- (g’4)

ために
 解決。フラットケースのように、標準化方程式もここに追加されています
解決。フラットケースのように、標準化方程式もここに追加されています
 さらに、Cramerルールの助けを借りてLGSを解決します。略語で
さらに、Cramerルールの助けを借りてLGSを解決します。略語で
-

-


四面体に関するバリゼ中心の座標(部屋)
あなたはバリア中心の座標を得ることができます
 :
:
- (BV4)

ある
 与えられた四面体から生じるディビッドトラヘドロンの量
与えられた四面体から生じるディビッドトラヘドロンの量
 終えた
終えた
 交換(写真を参照)。
交換(写真を参照)。
声明 (BV4) それは 教育率 §25、p。28、Möbiusの本。
は
 ベースエリア(四面体の側面エリア)と
ベースエリア(四面体の側面エリア)と
 の高さ
の高さ
 -Divertraedersを入手するので、適用されます
-Divertraedersを入手するので、適用されます
 と
と

特別なポイント [ 編集 | ソーステキストを編集します ]
- 幾何学的なフォーカス
幾何学的な焦点はです
 。そうです
。そうです
-

したがって
 与えられた四面体のボリュームと
与えられた四面体のボリュームと
 の高さ
の高さ
 – それ以上のポイント
– それ以上のポイント
 – テンサイドトライアングル(写真を参照)。したがって、以下が適用されます。
– テンサイドトライアングル(写真を参照)。したがって、以下が適用されます。
-

(レベルの場合の対応するステートメントを比較してください。)
- インクマー媒体
inhugelの中心はそうです
 (インクの半径)
(インクの半径)
-
 と
と
-

したがって
 与えられた四面体の体積はです。
与えられた四面体の体積はです。
- 座標レベルへのポイントの投影
フラットケース(上記参照)に類似しているのは、ポイントの投影です
 から
から
 反対のレベルから
反対のレベルから
 (彼女には方程式があります
(彼女には方程式があります
 ))))
))))
ポイント
 。の座標の場合
。の座標の場合
 標準化 共有
標準化 共有
 距離
距離
 に関して
に関して
 。他の3つの投影にも同じことが当てはまります。
。他の3つの投影にも同じことが当てはまります。
コマンドーノ文 [ 編集 | ソーステキストを編集します ]


:四面体の焦点、

:三角形の焦点
幾何学的な焦点を投影します
 から
から
 方程式のある反対のレベルから
方程式のある反対のレベルから
 、焦点を当てます
、焦点を当てます
 三角形の
三角形の
 。同じことが他の投影にも当てはまります
。同じことが他の投影にも当てはまります
 。そのため、適用されます(前のセクションを参照):
。そのため、適用されます(前のセクションを参照):
- ちょうど角の通り
 そして幾何学的な焦点
そして幾何学的な焦点
 反対の三角レベルは、四面体を焦点で削減します
反対の三角レベルは、四面体を焦点で削減します
 三角形の。分裂します
三角形の。分裂します
 距離
距離
 に関して
に関して
 。
。
これは コマンドーノ文 。
四面体のポイントを通る双曲線 [ 編集 | ソーステキストを編集します ]

単一の双曲体上の四面体
単一の双曲線は、2つの群衆の直線を含む四重鉄です。適切な均一な座標では、方程式を通じてそれを行うことができます
- (h)

説明 [6] (摂取双曲線を参照)。双曲線にはポイントが含まれています
-

-

それは簡単に計算されます
- (pH)

双曲線のパラメーター表現はです。以下が適用されます。
-
 と
と
-

パラメーター行(
 = constまたは
= constまたは
 = const)はまっすぐです。バリア中心座座標の合計は常に
= const)はまっすぐです。バリア中心座座標の合計は常に
 ただし、レベル上の双曲線のポイント
ただし、レベル上の双曲線のポイント
 記録されていません。これは、Bary Centerの導入の場合は不利ではありません。
記録されていません。これは、Bary Centerの導入の場合は不利ではありません。
要約します
 いつ バリーセンター 座標、ポイントに対応します
いつ バリーセンター 座標、ポイントに対応します
 双曲線上の四面体(アフィンルーム)の角
双曲線上の四面体(アフィンルーム)の角
 、それはストレートです
、それはストレートです
 含む(写真を参照)。 2つのストレート
含む(写真を参照)。 2つのストレート
 双曲線にはありません!標準化されたバリアン中心座標をアフィン座標に計算した場合(参照 (s) セクションで 意味 )、あなたは アフィンパラメーター表現 双曲線:
双曲線にはありません!標準化されたバリアン中心座標をアフィン座標に計算した場合(参照 (s) セクションで 意味 )、あなたは アフィンパラメーター表現 双曲線:
- (aph)

これは双曲線ASの表現です 双線形補間エリア きらめく広場の
 。
。
- 特性
双曲線にはリモートレベルがあります
 ポイントの2つ
ポイントの2つ
 直線を切る
直線を切る
-

-

一緒に、したがってaffinです
- 双曲線放物線。 (したがって、上記の写真は射影的に理解されるべきです。)
- 遠いレベルはポイントの接線レベルです
 。
。
- 焦点
 四面体は双曲線にあります。
四面体は双曲線にあります。
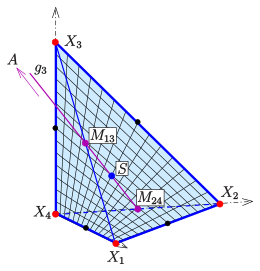
座標軸の上の点を備えた四面体の角を通る四頭岩の双曲線パラボロイド(射影インテリジェント双列のアフィナー部分)
真っ直ぐ
 センターを通過します
センターを通過します
 そこにはテトレインの端があります
そこにはテトレインの端があります
 また。
また。
 そして、長い距離を通ります
そして、長い距離を通ります
 。これはaffinを意味します:
。これはaffinを意味します:
- 双曲線のパラボロイド上のパラベルの軸はすべて直線に平行です
 センターを通して
センターを通して
 (双曲線放物線を参照)。焦点
(双曲線放物線を参照)。焦点
 ポイントの中心です
ポイントの中心です
 。
。
- 例
写真は、の例を示しています
-

-

パラメーター表現は次のとおりです
-

バリア中心座座
 シンプレックスの代わりにポリトップを参照して定義されています 一般化されたバリーセンター座標 呼び出されました。ここでは、方程式がまだ必要です
シンプレックスの代わりにポリトップを参照して定義されています 一般化されたバリーセンター座標 呼び出されました。ここでは、方程式がまだ必要です
-

それによって満たされます
 与えられたポリトップの礎石です。したがって、定義は正式に変更されていませんが、シンプレックスは
与えられたポリトップの礎石です。したがって、定義は正式に変更されていませんが、シンプレックスは
 少なくとも寸法があるベクトルルームのコーナーポイント
少なくとも寸法があるベクトルルームのコーナーポイント
 封じ込められていますが、ポリトープは低寸法のベクトルに埋め込むこともできます。最も単純な例は、レベルの正方形です。結果として、ポリトップの標準化された一般化された核心座標でさえ、一般に明確に決定されていませんが、これはシンプレックスを参照した標準化されたバリゼ中心座座標の場合です。
封じ込められていますが、ポリトープは低寸法のベクトルに埋め込むこともできます。最も単純な例は、レベルの正方形です。結果として、ポリトップの標準化された一般化された核心座標でさえ、一般に明確に決定されていませんが、これはシンプレックスを参照した標準化されたバリゼ中心座座標の場合です。
一般化された核心座標は、特にコンピューターグラフィックスおよび幾何学モデリングで使用されます。そこでは、3つの次元オブジェクトをPolyhedraによって近似することが多いため、一般化されたバリーセンター座標は幾何学的な意味を持ち、これらのオブジェクトのさらなる処理を促進します。
補間手順は、いくつかの変数の関数の線形補間を一般化する核心座標に基づいています。
関数の場合
 2つの変数の
2つの変数の
 と
と
 3つのポイントです
3つのポイントです
 、
、
 と
と
 与えられた機能値。そうすることで
与えられた機能値。そうすることで
 、
、
 と
と
 直線ではありません。したがって、あなたは三角形をしなければなりません
直線ではありません。したがって、あなたは三角形をしなければなりません
 留め金。今ではどんなポイントです
留め金。今ではどんなポイントです
 与えられた、あなたは定義します
与えられた、あなたは定義します
-
 、
、
したがって
 の標準化されたバリア中心座座標
の標準化されたバリア中心座座標
 それは。この補間は、三角形の外側のポイントでも機能します。
それは。この補間は、三角形の外側のポイントでも機能します。
- Oswin Aichholzer、BertJütttler: 適用されたジオメトリの概要。 Springer-Verlag、バーゼル2013、doi: 10,1007/978-3-0346-0651-6 、ISBN 978-3-0346-0651-6-6- S. 59。
- ジェラルドファリン、ダイアンハンスフォード: 線形代数:幾何学的アクセス。 Springer-Verlag、2013、doi: 10,1007/978-3-642-5841-2-2 、ISBN 978-3-540-41854-2、p。139。
- ジョン・ファウベル、レイモンド・フラッド、ロビン・ウィルソン: Möbiusと彼のバンド:19世紀のドイツでの数学と天文学の台頭。 Springs-Publising、2013、ICHN 978-3-0348-6203-5、S。106。
- ピーター・ナブナー、ルッツ・アンガルマン: numerik部分微分方程式。アプリケーション指向の紹介。 Springer 2000、ISBN 3-642-57181-6、S。108–111( books.google.de )。
- アブラハムa。ウンガー: ユークリッドおよび双曲線の幾何学における口径の計算。 World Scientific 2010、ISBN 978-981-4304-93-1。
- ジョン・ヴィンス: コンピューターグラフィックスの数学。 Springer 2010、ISBN 978-1-84996-032-8、S。208–236。
- ↑ マックス・コチャー、アロイの戦争: レベルジオメトリ。 Springs-Publis、Berlin 2007、ISBN 978-3-540-49328-0、PL 76。
- ↑ August FerdinandMöbius: Barechnurch Calcul 、ヨハン・アンブロシウス・バースによる出版社、ライプツィヒ、1827年。
- ↑ Josef Hoosch、Dieter Lock: データ処理の幾何学の基礎。 Teubner-Verlag、1989、ISBN 3-519-02962-6、p。243。
- ↑ ジェラルドホワイト: コンピューター支援の幾何学デザインの曲線とサーフィン。 Academic Press、1990、ISBN 0-12-249051-7、S。20。
- ↑ クリスチャン・ゲルセン: 物理。 Springer-Verlag、1963、p。37。
- ↑ フェリックスクライン: より高いジオメトリに関する講義 、Springr-Publisher、2013年
ISBN 3642886744、97836428686744、P。
























 あなたは3つの質量の状況になることができます
あなたは3つの質量の状況になることができます  与えられた三角形の角にあるそれを紹介し、それらの焦点
与えられた三角形の角にあるそれを紹介し、それらの焦点  。すべての質量が同じ場合、そうです
。すべての質量が同じ場合、そうです  。口径の座標は、次の特性を通じて幾何学的な意味を受け取ります。1次元では、質量比は部分的な距離の比率(2番目の画像を参照)であり、2次元では、質量条件は部分的な三角形の表面条件です。
。口径の座標は、次の特性を通じて幾何学的な意味を受け取ります。1次元では、質量比は部分的な距離の比率(2番目の画像を参照)であり、2次元では、質量条件は部分的な三角形の表面条件です。  それ以外の
それ以外の  。
。  コーナーのローカルベクター
コーナーのローカルベクター  アフィンルームの1つのシンプルです
アフィンルームの1つのシンプルです  。アフィンスペースには次元があります
。アフィンスペースには次元があります  。ポイントの場合
。ポイントの場合  の
の  その合計はゼロではなく、方程式を与えます
その合計はゼロではなく、方程式を与えます 
 それは バリア中心座座 ポイント
それは バリア中心座座 ポイント  ポイントに関して
ポイントに関して  と書いています
と書いています  。明らかに角に適用されます
。明らかに角に適用されます 
 また、多くのゼロについて説明します
また、多くのゼロについて説明します  ポイント
ポイント  覚えて。 Bary Centered Coordinatesは、の均一な座標として使用できます
覚えて。 Bary Centered Coordinatesは、の均一な座標として使用できます  – 次元射影空間
– 次元射影空間  アフィンルームから取り出します
アフィンルームから取り出します  特定のハイパーベール(リモートハイパーテイクレベル)です。
特定のハイパーベール(リモートハイパーテイクレベル)です。 
 加えて 標準化条件
加えて 標準化条件 
 明らかに 決定(以下を参照)とできます
明らかに 決定(以下を参照)とできます  Hypereneath Desk
Hypereneath Desk  方程式で
方程式で  取った。
取った。 オン、結果
オン、結果  。
。 
 標準化 (!)2つのポイントのバリーセンター表現
標準化 (!)2つのポイントのバリーセンター表現  、次にセンター
、次にセンター  バリーセンターの表現
バリーセンターの表現 
 適用されます。
適用されます。  固定ベクトルへ
固定ベクトルへ  定義方程式 (g) 変わらないままにします。同じことが均一なスケーリングにも当てはまります(固定係数を不均一に伴うベクターの乗算)。
定義方程式 (g) 変わらないままにします。同じことが均一なスケーリングにも当てはまります(固定係数を不均一に伴うベクターの乗算)。  そして、各ポイントには3つのバリア中心の座標があります。
そして、各ポイントには3つのバリア中心の座標があります。  。たとえば、三角形の幾何学的焦点にはバリーセンターの表現があります
。たとえば、三角形の幾何学的焦点にはバリーセンターの表現があります  、 その理由は
、 その理由は  標準化された表現はです
標準化された表現はです 
 説明されています。これには、関連するアフィンレベル(長い距離のポイントなしの射影レベル)を説明するアフィン座標への単純な接続が存在するという利点があります。
説明されています。これには、関連するアフィンレベル(長い距離のポイントなしの射影レベル)を説明するアフィン座標への単純な接続が存在するという利点があります。  。ただし、座標軸に属する射影点が
。ただし、座標軸に属する射影点が  アフィンポイントではありません。ポイントだけ
アフィンポイントではありません。ポイントだけ  アフィンポイントになります。バリゼ中心の座標は、アフィン座標とそのような簡単な関係はありません。このため、座標軸に対応するすべての射影点は
アフィンポイントになります。バリゼ中心の座標は、アフィン座標とそのような簡単な関係はありません。このため、座標軸に対応するすべての射影点は  アフィン領域では、長い距離ストレートは方程式を通過するため
アフィン領域では、長い距離ストレートは方程式を通過するため  説明された。
説明された。  2つの質量
2つの質量  – 場所の軸
– 場所の軸  配置されている、場所はそうです
配置されている、場所はそうです  、レバレッジ法( パワー×パワーアーム=負荷×ロードアーム 、2番目の写真を参照)が満たされています。より正確には:トルクの合計がゼロの場合 [5] そしてそれで:
、レバレッジ法( パワー×パワーアーム=負荷×ロードアーム 、2番目の写真を参照)が満たされています。より正確には:トルクの合計がゼロの場合 [5] そしてそれで: 


 、これが結果です (G2) ために
、これが結果です (G2) ために  総質量
総質量  と
と  。
。  。すべてのソリューションはそれらの複数です。したがって、焦点はバリーセンターの表現にあります(セクションを参照してください 意味 ))
。すべてのソリューションはそれらの複数です。したがって、焦点はバリーセンターの表現にあります(セクションを参照してください 意味 )) 





 ポイント
ポイント  標準化された表現で
標準化された表現で 
 3つの質量
3つの質量 


 、未定の均一なシステムを緩めることで得ます (G’3) 後
、未定の均一なシステムを緩めることで得ます (G’3) 後 











 参照の三角形にはポイントがあります
参照の三角形にはポイントがあります  シンプルなバリーセンター座標
シンプルなバリーセンター座標  。
。 





 。
。 
 。
。 





 、それによって
、それによって  基本(三角形のページ)と部分三角形の高さは(写真を参照)です。適用されます
基本(三角形のページ)と部分三角形の高さは(写真を参照)です。適用されます 
 ポイントの。正女の三角形の場合、バリーセンターと三線座標は同じです。長い距離ストレートには、バリゼ中心の座標の方程式があります
ポイントの。正女の三角形の場合、バリーセンターと三線座標は同じです。長い距離ストレートには、バリゼ中心の座標の方程式があります  。三線座標では、方程式はまだ辺の長さからです
。三線座標では、方程式はまだ辺の長さからです  三角形の:
三角形の: 
 なぜなら (BF3) と
なぜなら (BF3) と  適用可能です
適用可能です 

 ポイントを用意しています
ポイントを用意しています  表現
表現 
 角から
角から  反対側から(これは現在方程式です
反対側から(これは現在方程式です  )、だからあなたはポイントを得る
)、だからあなたはポイントを得る  (画像を参照)。の座標です
(画像を参照)。の座標です  に関して
に関して  。
。 ルートを投影して共有します
ルートを投影して共有します  に関して
に関して  。
。 

 (inkreisradius)、したがって(参照してください。 (BT3) )回路の中心には、核心座標があります
(inkreisradius)、したがって(参照してください。 (BT3) )回路の中心には、核心座標があります  そして、
そして、  適用可能です
適用可能です  副鼻腔セットの助けを借りて、角度を持つ表現も回路中心の結果として生じます。
副鼻腔セットの助けを借りて、角度を持つ表現も回路中心の結果として生じます。 
 角度
角度  は。
は。  (真っ直ぐ
(真っ直ぐ  )方程式があります
)方程式があります 
 (方程式
(方程式  。 (
。 (  投影としても可能です
投影としても可能です  側面上
側面上 
 そしてそれもそれで
そしてそれもそれで  負の値を受け入れるかどうか
負の値を受け入れるかどうか 




 明らかにポイントの投影(上記を参照)です
明らかにポイントの投影(上記を参照)です 



 (セクションSteiner-Ellipse、Steiner-Inllipseを参照)。あなたが形成します
(セクションSteiner-Ellipse、Steiner-Inllipseを参照)。あなたが形成します 


 、半径。角度
、半径。角度  円形の角度が設定されているため、角度の2倍の大きさです
円形の角度が設定されているため、角度の2倍の大きさです  で
で  。同じことが当てはまります
。同じことが当てはまります  。これは、センタリングポイントのバリーセンター座標が
。これは、センタリングポイントのバリーセンター座標が 
 そして、3つの角度のコジナーは、角度のない表現につながります
そして、3つの角度のコジナーは、角度のない表現につながります 

 高さのカットポイント、そうです
高さのカットポイント、そうです  高さのベースポイント
高さのベースポイント  (写真を参照)、適用されます
(写真を参照)、適用されます  なぜなら (B2) は
なぜなら (B2) は  同様に、他の状況が発生します。これは、高さ-CUTポイントにバリーセンターの座標があることを意味します
同様に、他の状況が発生します。これは、高さ-CUTポイントにバリーセンターの座標があることを意味します 
 そうです。 B.
そうです。 B.  、そうです
、そうです  。
。  三角形
三角形  集中して、Spieker Pointはそうです
集中して、Spieker Pointはそうです  三角形の焦点
三角形の焦点  サイドの長さで
サイドの長さで  角の大量割り当てとして。 out
角の大量割り当てとして。 out  と (S3) フォロー:
と (S3) フォロー: 


 三角形の場合
三角形の場合 
 ポイントの長さ
ポイントの長さ 


 は。
は。  、したがって、オイラーガレードには方程式があります
、したがって、オイラーガレードには方程式があります  サイトの側面と同じです
サイトの側面と同じです  そして、オイラーガレードには方程式があります
そして、オイラーガレードには方程式があります  ストレートの交点
ストレートの交点  側面で
側面で  (写真を参照)、適用されます
(写真を参照)、適用されます 


 (ご参照ください 特別なポイント )。 out B2 あなたは得ます
(ご参照ください 特別なポイント )。 out B2 あなたは得ます  また、ポイントに対するこれらの考慮事項をリードする場合
また、ポイントに対するこれらの考慮事項をリードする場合  スルー、結果
スルー、結果 



 センター(セクションを参照してください 意味 )カップル
センター(セクションを参照してください 意味 )カップル  は。方程式 (se) だから、コーンの外ではない必要があります
は。方程式 (se) だから、コーンの外ではない必要があります  (楕円またはハイパーベルまたは放物線)説明。式から
(楕円またはハイパーベルまたは放物線)説明。式から 



 そして、それによって楕円の不変(楕円は5つのポイントによって明確に決定されます)。したがって、対称ポイントはそうです
そして、それによって楕円の不変(楕円は5つのポイントによって明確に決定されます)。したがって、対称ポイントはそうです  腱
腱  )楕円で (se) あなたも2つを手に入れます
)楕円で (se) あなたも2つを手に入れます 
 彼らの中心で
彼らの中心で  の画像マトリックスです
の画像マトリックスです 

 の中に
の中に  (いつものように) オルソゴナレン 座標軸は、座標軸とストレートを含む先端としてゼロポイントを持つまっすぐな円形コーンです
(いつものように) オルソゴナレン 座標軸は、座標軸とストレートを含む先端としてゼロポイントを持つまっすぐな円形コーンです  軸としてあります。なぜなら、レベルの交差曲線のため
軸としてあります。なぜなら、レベルの交差曲線のため 

 見せる:
見せる:  (写真の緑)。コーンを切ります
(写真の緑)。コーンを切ります  、起源をまっすぐにします
、起源をまっすぐにします  、d。 H.コーンは座標レベルに触れます。これは、他のレベルの座標にも適用されます。
、d。 H.コーンは座標レベルに触れます。これは、他のレベルの座標にも適用されます。  、これが方程式の説明方法です (se) アフィンエリア(
、これが方程式の説明方法です (se) アフィンエリア(  )ハイパーベルをダイ
)ハイパーベルをダイ  。この場合、ポイントは次のとおりです
。この場合、ポイントは次のとおりです  導入。
導入。  。ポイントのバリーセンター座標に
。ポイントのバリーセンター座標に  2次元の場合(三角形)、均一な線形方程式システムに類似した、与えられた四面体の決定(セクションを参照 意味 ))
2次元の場合(三角形)、均一な線形方程式システムに類似した、与えられた四面体の決定(セクションを参照 意味 )) 
 解決。フラットケースのように、標準化方程式もここに追加されています
解決。フラットケースのように、標準化方程式もここに追加されています  さらに、Cramerルールの助けを借りてLGSを解決します。略語で
さらに、Cramerルールの助けを借りてLGSを解決します。略語で 


 与えられた四面体から生じるディビッドトラヘドロンの量
与えられた四面体から生じるディビッドトラヘドロンの量  終えた
終えた  -Divertraedersを入手するので、適用されます
-Divertraedersを入手するので、適用されます  と
と 
 。そうです
。そうです 
 与えられた四面体のボリュームと
与えられた四面体のボリュームと  の高さ
の高さ 


 与えられた四面体の体積はです。
与えられた四面体の体積はです。  から
から  反対のレベルから
反対のレベルから  (彼女には方程式があります
(彼女には方程式があります  ))))
)))) 。の座標の場合
。の座標の場合  に関して
に関して  。他の3つの投影にも同じことが当てはまります。
。他の3つの投影にも同じことが当てはまります。 
 から
から  三角形の
三角形の  。同じことが他の投影にも当てはまります
。同じことが他の投影にも当てはまります 







 = constまたは
= constまたは  = const)はまっすぐです。バリア中心座座標の合計は常に
= const)はまっすぐです。バリア中心座座標の合計は常に  ただし、レベル上の双曲線のポイント
ただし、レベル上の双曲線のポイント  記録されていません。これは、Bary Centerの導入の場合は不利ではありません。
記録されていません。これは、Bary Centerの導入の場合は不利ではありません。  双曲線上の四面体(アフィンルーム)の角
双曲線上の四面体(アフィンルーム)の角  、それはストレートです
、それはストレートです  含む(写真を参照)。 2つのストレート
含む(写真を参照)。 2つのストレート  双曲線にはありません!標準化されたバリアン中心座標をアフィン座標に計算した場合(参照 (s) セクションで 意味 )、あなたは アフィンパラメーター表現 双曲線:
双曲線にはありません!標準化されたバリアン中心座標をアフィン座標に計算した場合(参照 (s) セクションで 意味 )、あなたは アフィンパラメーター表現 双曲線: 
 直線を切る
直線を切る 



 センターを通過します
センターを通過します  そこにはテトレインの端があります
そこにはテトレインの端があります  また。
また。  そして、長い距離を通ります
そして、長い距離を通ります 





 シンプレックスの代わりにポリトップを参照して定義されています 一般化されたバリーセンター座標 呼び出されました。ここでは、方程式がまだ必要です
シンプレックスの代わりにポリトップを参照して定義されています 一般化されたバリーセンター座標 呼び出されました。ここでは、方程式がまだ必要です 
 2つの変数の
2つの変数の  3つのポイントです
3つのポイントです  、
、  と
と  与えられた機能値。そうすることで
与えられた機能値。そうすることで  と
と  直線ではありません。したがって、あなたは三角形をしなければなりません
直線ではありません。したがって、あなたは三角形をしなければなりません  留め金。今ではどんなポイントです
留め金。今ではどんなポイントです 
 の標準化されたバリア中心座座標
の標準化されたバリア中心座座標
Recent Comments