eulersche番号 、シンボルで
 記載されているのは、分析全体と数学のすべてのサブエリア、特に差動および積分計算でも、石依存症(組み合わせ、正規分布)において中心的な役割を果たしている定数です。あなたの数値はです
記載されているのは、分析全体と数学のすべてのサブエリア、特に差動および積分計算でも、石依存症(組み合わせ、正規分布)において中心的な役割を果たしている定数です。あなたの数値はです
-
 [初め]
[初め]
 は超越的であり、したがって不合理な実数です。これは、自然対数と(自然な)指数関数の基礎です。適用された数学、指数関数、したがって
は超越的であり、したがって不合理な実数です。これは、自然対数と(自然な)指数関数の基礎です。適用された数学、指数関数、したがって
 放射性崩壊や自然成長などのプロセスの説明における重要な役割。
放射性崩壊や自然成長などのプロセスの説明における重要な役割。
の多数の同等の定義があります
 、最もよく知られているのは次のとおりです。
、最もよく知られているのは次のとおりです。
-

この番号は、スイスの数学者レオンハルトオイラーにちなんで名付けられました、 [2] の多数の特性
 説明された。時々彼女はスコットランドの数学者ジョン・ネイピアの後に ネイピアの定数 (また Neperscheは永久に ) 専用。数学の最も重要な定数の1つです。
説明された。時々彼女はスコットランドの数学者ジョン・ネイピアの後に ネイピアの定数 (また Neperscheは永久に ) 専用。数学の最も重要な定数の1つです。
オイラー番号の国際的な日があります
 。ドイツのように、その月前(1月27日)の前日(1月27日)にある国では、1月27日です。 [3] 2月7日に1日前(2/7)が書かれた国で。
。ドイツのように、その月前(1月27日)の前日(1月27日)にある国では、1月27日です。 [3] 2月7日に1日前(2/7)が書かれた国で。
人数、個数、総数
 Leonhard Eulerによって次のシリーズで定義されました。 [4]
Leonhard Eulerによって次のシリーズで定義されました。 [4]
-

ために
 入っています
入っています
 の教員
の教員
 、その場合
、その場合

 の自然数
の自然数
 それまで
それまで
 、 その間
、 その間
 定義されています。
定義されています。
オイラーがすでに実証しているように、あなたはオイラーシュ番号を取得します
 機能的な制限としても。 [5]
機能的な制限としても。 [5]
人数、個数、総数
 エピソードの限界でもあります
エピソードの限界でもあります
 と
と
 書かれる:
書かれる:
-

これはそれに基づいています
-

該当する、
 したがって、指数関数の関数値(または」
したがって、指数関数の関数値(または」
 -Function」)ポイントで
-Function」)ポイントで
 は。上記のシリーズプレゼンテーション
は。上記のシリーズプレゼンテーション
 これに関連して、開発機関の周りの指数関数のテイラーシリーズが見つかるという事実に起因します
これに関連して、開発機関の周りの指数関数のテイラーシリーズが見つかるという事実に起因します
 ポイントで
ポイントで
 評価された。
評価された。
オイラー番号の定義への代替アクセスは、たとえば途中でインターバルボックスに関するものです。 無限行の理論と適用 Konrad Knoppによって示されています。その後、すべての人に当てはまります
 : [6]
: [6]
-

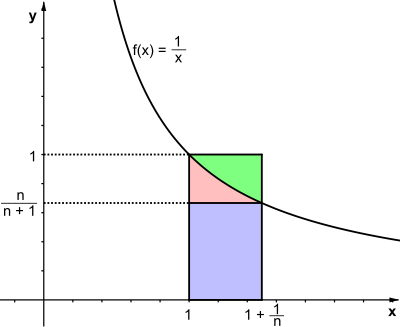
数の出現
 グラフィカルに説明することもできます。次のコンテキストは、図の結果です [7] :
グラフィカルに説明することもできます。次のコンテキストは、図の結果です [7] :
-

-
 (積分の解決策)
(積分の解決策)
-
 (nとの乗算)
(nとの乗算)
-
 (対数法の適用)
(対数法の適用)
-
 (値の形成を制限)
(値の形成を制限)
-
 (対数関数のスタンドネス)
(対数関数のスタンドネス)
-
 (反転関数の指数関数)
(反転関数の指数関数)
オイラー番号の歴史
 16世紀には3つの問題領域がある16世紀に始まり、その中に数学者に近づいた数字が現れました。
16世紀には3つの問題領域がある16世紀に始まり、その中に数学者に近づいた数字が現れました。
 と呼ばれていました:
と呼ばれていました:
- John NapierとJostBürgiによる対数ボードの対数の基礎として。両方とも、マイケル・スティフェルの録音と16世紀の他の数学者の結果によるアイデアを使用して、互いに独立してテーブルを開発していました。 Bürgiは1620年に「算術と幾何学的プログラムのタブール」を公開しました。彼の対数システムの基礎として、Bürgiは明らかに本能的に近くの数字を使用しています
 嘘。 Napierは1614年に彼の「Mirifici logarithmorum canonis記述」を公開し、1つを使用します
嘘。 Napierは1614年に彼の「Mirifici logarithmorum canonis記述」を公開し、1つを使用します
 比例基準。 [8] 対数テーブルの助けを借りて、NapierとBürgiは、膨大な請求書をより簡単で時間を短縮するために、増加を加算に追跡したいと考えていました。
比例基準。 [8] 対数テーブルの助けを借りて、NapierとBürgiは、膨大な請求書をより簡単で時間を短縮するために、増加を加算に追跡したいと考えていました。
- 複利のシーケンスの制限として。 1669年、ヤコブ・ベルヌーリはタスクを提供しました:「年間利息の比例部分が個々の瞬間に首都に打ちのめされたという利息の金額が創出されました。 [9] Bernoulliは、個々の瞬間が短くて短くなっている契約が開始額の倍数を達成できるかどうかを尋ね、解決策として、私たちは今日のEulersche番号としての数に達します
 知る。 [十]
知る。 [十]
- 無限のシリーズとして(ペルゲのアポロニオの双曲線の領域)。それは(今日の言語で)ハイパーベルの下の領域の問題でした
 から
から
 右に伸びます。これは、ユニットスクエアの面積と同じ大きさです。フランドルの数学者グレゴワール・デ・サン・ビンセント(ラテン化グレゴリウス・サンクト・ヴィンセンティーノ)は、私たちが今日呼び、自然対数を使用してソリューションのための機能を開発しました
右に伸びます。これは、ユニットスクエアの面積と同じ大きさです。フランドルの数学者グレゴワール・デ・サン・ビンセント(ラテン化グレゴリウス・サンクト・ヴィンセンティーノ)は、私たちが今日呼び、自然対数を使用してソリューションのための機能を開発しました
 説明。彼は、今日私たちが対数の機能方程式と呼ぶ方程式を含む興味深い特性を発見しました。 [11] 彼がこの対数の根拠が後の数字であることを彼が知っていたかどうかは確かではありません
説明。彼は、今日私たちが対数の機能方程式と呼ぶ方程式を含む興味深い特性を発見しました。 [11] 彼がこの対数の根拠が後の数字であることを彼が知っていたかどうかは確かではありません
 と呼ばれていました。これは、彼の作品が公開された後にのみ気づきました。 [12番目] 最新の状態では、彼の学生であり共著者であるAlphonse Antonio de Sarasaが対数関数とのつながりを提示しました。DeSarasaを通じてSaint-Vincentのアイデアのspread延を扱うエッセイでは、「ロルガリットとハイパーベルの関係は、サンヴィンシントによってあらゆる特性に見られた」と言われています。 [13] ニュートンとオイラーで働くことで、
と呼ばれていました。これは、彼の作品が公開された後にのみ気づきました。 [12番目] 最新の状態では、彼の学生であり共著者であるAlphonse Antonio de Sarasaが対数関数とのつながりを提示しました。DeSarasaを通じてSaint-Vincentのアイデアのspread延を扱うエッセイでは、「ロルガリットとハイパーベルの関係は、サンヴィンシントによってあらゆる特性に見られた」と言われています。 [13] ニュートンとオイラーで働くことで、
 基礎はです。 [14] ライプニッツは、明らかにこの番号に手紙を使用した最初の人物でした。 1690/1年からのChristiaan Huygensとの通信で、彼は文字Bを効力の基礎として使用しました。 [15]
基礎はです。 [14] ライプニッツは、明らかにこの番号に手紙を使用した最初の人物でした。 1690/1年からのChristiaan Huygensとの通信で、彼は文字Bを効力の基礎として使用しました。 [15]
文字を使用するために使用される最も初期のドキュメントとして
 レオンハルト・オイラーによるこの番号には、1731年11月25日からオイラーからクリスチャン・ゴールドバッハへの手紙が適用されます。 [16] さらに早く、1727年または1728年、オイラーは手紙を始めました
レオンハルト・オイラーによるこの番号には、1731年11月25日からオイラーからクリスチャン・ゴールドバッハへの手紙が適用されます。 [16] さらに早く、1727年または1728年、オイラーは手紙を始めました
 1862年にのみ公開された大砲の爆発力について、「実験爆発性爆発性トルメントーラムヌーパー研究所」の記事「瞑想」で使用するため。 [17] [18] この手紙を使用するための次の安全な情報源は、オイラーの作品です 分析的に暴露された機械的または感情的な科学2 1736年から。 [6] 1748年に公開されたもの 分析の紹介 オイラーは再びこの名前を拾います。 [19]
1862年にのみ公開された大砲の爆発力について、「実験爆発性爆発性トルメントーラムヌーパー研究所」の記事「瞑想」で使用するため。 [17] [18] この手紙を使用するための次の安全な情報源は、オイラーの作品です 分析的に暴露された機械的または感情的な科学2 1736年から。 [6] 1748年に公開されたもの 分析の紹介 オイラーは再びこの名前を拾います。 [19]
この手紙の選択の証拠はありません
 彼の名前に基づいています。また、彼が指数関数に基づいているのか、それとも使用されている文字への境界の実際的な考慮事項に基づいているのかは不明です。 A、B、c また d 作る。たとえば、他の名前も使用されていましたが c ダレンベールズで アカデミーの歴史、 もっている
彼の名前に基づいています。また、彼が指数関数に基づいているのか、それとも使用されている文字への境界の実際的な考慮事項に基づいているのかは不明です。 A、B、c また d 作る。たとえば、他の名前も使用されていましたが c ダレンベールズで アカデミーの歴史、 もっている
 強制。
強制。
フォーミュラセットはです
 DIN 1338およびISO 80000-2によると、数を変数と区別するための斜体ではありません。 [20] ただし、コースも広範囲に及びます。
DIN 1338およびISO 80000-2によると、数を変数と区別するための斜体ではありません。 [20] ただし、コースも広範囲に及びます。
Eulersche番号
 超越的です( 証拠 チャールズ・ヘルミス、1873年によると)、したがって非合理的な数(チェーンブレイクによる証明
超越的です( 証拠 チャールズ・ヘルミス、1873年によると)、したがって非合理的な数(チェーンブレイクによる証明
 したがって
したがって
 すでに1737年にオイラーによって、 [21] 証明 証明 – または記事)。だからそれは(そして回路の数と同様にそうかもしれません
すでに1737年にオイラーによって、 [21] 証明 証明 – または記事)。だからそれは(そして回路の数と同様にそうかもしれません
 Ferdinand von Lindemann 1882)によると、2つの自然数(代数方程式の解決策としても)の休憩としてではなく、その結果、無限の非周期フラグメント開発があります。の不合理性
Ferdinand von Lindemann 1882)によると、2つの自然数(代数方程式の解決策としても)の休憩としてではなく、その結果、無限の非周期フラグメント開発があります。の不合理性
 特に、不合理な数の場合はできるだけ小さい2つです
特に、不合理な数の場合はできるだけ小さい2つです
 liouvilleschではありません。かどうかは不明です
liouvilleschではありません。かどうかは不明です
 何らかの根拠が正常です。 [22]
何らかの根拠が正常です。 [22]
オイラーのアイデンティティで
-

基本的な数学定数に関連しています:整数1、eulersche番号
 、想像上のユニット
、想像上のユニット
 複雑な数と回路の数
複雑な数と回路の数
 。
。
Eulersche番号は、教員の漸近評価でも発生します(スターリングフォーミュラを参照)。 [23]
-

2つの(絶対に収束)列とビノミック教育率のコーシー製品の式
-

そしてこれからすぐに続きます:
-

オイラー数の幾何学的解釈は、積分計算を提供します。その後です
 明確に決定された数
明確に決定された数

 間隔で
間隔で
![{displaystyle [1,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8771aaef108f3cf1381367f4874c74ae7b5e9aa5) まったく同じ
まったく同じ
 は: [24]
は: [24]
-

Eulersche番号も実行できます
-
![e = lim_{ntoinfty} frac{n}{sqrt[n]{n!}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/310afedad5e855a28eb0d1b232a29031bd682548)
または、教員と副省からの商の限界で説明してください。
-

素数の分布への接続は式を介して行われます
-
![e = lim_{n to infty} (sqrt[n]{n})^{pi(n)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d630cbe58c254c4dc64710f9a81dacddc9897d8)
-
![e = lim_{n to infty} sqrt[n]{n#}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a49850b48669d471e09b151b3ef18f0a81e87344)
明らかに、しかし
 素数関数とシンボル
素数関数とシンボル
 数字の原始
数字の原始
 意味。
意味。
また、実際的に重要なエキゾチックな刺激の方が カタロニアの表現
-
![e=sqrt[1]{frac{2}{1}}cdotsqrt[2]{frac{4}{3}}cdotsqrt[4]{frac{6cdot 8}{5cdot 7}}cdotsqrt[8]{frac{10cdot 12cdot 14cdot 16}{9cdot 11cdot 13cdot 15}}cdots](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e598bf5c258b6349e3cd7adfe125b915e77dbd4)
番号に関連して
 最新のレオンハルトオイラーズの出版以来存在しています 分析の紹介 1748年、多くのチェーンブレイク開発が
最新のレオンハルトオイラーズの出版以来存在しています 分析の紹介 1748年、多くのチェーンブレイク開発が
 そしてから
そしてから
 派生可能なサイズ。
派生可能なサイズ。
したがって、オイラーには次の古典的なアイデンティティがあります
 見つかった:
見つかった:
-
![{displaystyle (1){begin{aligned}e&=[2;1,2,1,1,4,1,1,6,1,1,8,1,1,10,1,dotsc ]\&=2+{cfrac {1}{1+{cfrac {1}{2+{cfrac {1}{1+{cfrac {1}{1+{cfrac {1}{4+{cfrac {1}{1+{cfrac {1}{1+{cfrac {1}{6+dotsb }}}}}}}}}}}}}}}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5ec3169e1a05da55f303dc18cd87060421a9b8a) (結果 A003417 OEISで)
(結果 A003417 OEISで)
アイデンティティ(1)には、無限に続く規則的なパターンがあるようです。これは、オイラーによって以下から派生した定期的なチェーンブレイクを反映しています。 [25]
-
![{displaystyle (2){begin{aligned}{frac {e+1}{e-1}}&=[2;6,10,14,dotsc ]\&={2+{cfrac {1}{6+{cfrac {1}{10+{cfrac {1}{14+{cfrac {1}{;,ddots }}}}}}}}}\&approx 2{,}1639534137386end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5fa822639e5939f4fa0b49836a70f10e4470da43) (結果 A016825 OEISで)
(結果 A016825 OEISで)
次に、このチェーンブレイクは次の特別なケースです
 :
:
-
![{displaystyle (3){begin{aligned}{coth {frac {1}{k}}}&={frac {e^{frac {2}{k}}+1}{e^{frac {2}{k}}-1}}\&=[k;3k,5k,7k,dots ]\&={k+{cfrac {1}{3k+{cfrac {1}{5k+{cfrac {1}{7k+{cfrac {1}{;,ddots }}}}}}}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12af66797cccd4b577eb60dc5ff4b0147a0a6cd2)

しかし、別の古典的なチェーンブレイク開発、しかし、それは 規制ではありません オイラーからのものでもあります: [26]
-
 (結果 A073333 OEISで)
(結果 A073333 OEISで)
の別のチェーン破壊 Eulerschen番号 バック、これは(1)以外のパターンからのものです。 [27]
-

に関連して Eulerschen番号 また、多数の一般的なチェーンルーチ理論方程式があります。 Oskar Perronは次の一般的に適用可能なプレゼンテーションに名前を付けます
 -関数: [27]
-関数: [27]
-


この別の例は、ヨハン・ハインリッヒ・ランバートから来ている、タンジングハイパーボリクスの発展です ランバートのチェーンが壊れます 期待されています: [28] [29]
-


Srinivasa Ramanujanがコンピュータープログラムの助けになったのは2019年だけでした ラマヌジャンマシン 最終的には、裁判とテロリストの方法に基づいて、Gal Raayoniが率いるチームがテクニオンで率いるチームは、Eulersche番号の別の、以前は未知のチェーンブレイク開発の開発方法に基づいて名前が付けられました。以前に既知のすべてのチェーンブレイキング開発と比較して、オイラー数よりも小さい整数のすべてが初めてです 3 、オイラーシュ数よりも大きい整数。 [30] オイラー番号よりも大きい整数からそのような下降チェーンブレイクを(単一)見つけるだけ

 と
と


金利計算 [ 編集 | ソーステキストを編集します ]
次の例では、オイラー数の計算がより記述的になるだけでなく、オイラー数の発見の歴史についても説明しています。彼らの最初の場所は、複利を調べる際にヤコブ・アイ・ベルヌーリによって発見されました。
最初の式の限界は次のように解釈できます。誰かが1月1日にベンチで1ユーロを支払うでしょう。銀行は彼に金利に関する現在の利息を保証します
 1年当たり。来年の1月1日の彼が同じ条件で関心を生み出したとき、彼の信用はどれくらい大きいですか?
1年当たり。来年の1月1日の彼が同じ条件で関心を生み出したとき、彼の信用はどれくらい大きいですか?
複利式の後
 後
後
 金利の利息
金利の利息
 首都
首都
-

この例では
 と
と
 利息追加料金が毎年行われる場合、または
利息追加料金が毎年行われる場合、または
 利息追加料金の場合
利息追加料金の場合
 – プラスは今年、つまり今年に興味を持って行われます。
– プラスは今年、つまり今年に興味を持って行われます。
毎年の追加料金があります
-

半年間の追加料金であなたが持っています
 、
、
-

もう少し。毎日の金利
 あなたは得ます
あなたは得ます
-

関心が毎回継続的に行われている場合
 無限に大きく、上記の最初の式を取得します
無限に大きく、上記の最初の式を取得します
 。
。
確率計算 [ 編集 | ソーステキストを編集します ]
 また、確率理論でもよく見られます。たとえば、パン屋は各ロールの生地にレーズンを与え、それをよくこねると想定されています。その後、統計的には、それぞれにそれぞれが含まれます
また、確率理論でもよく見られます。たとえば、パン屋は各ロールの生地にレーズンを与え、それをよくこねると想定されています。その後、統計的には、それぞれにそれぞれが含まれます
 -teパンはレーズンなし。確率
-teパンはレーズンなし。確率
 それで
それで
 パンはどれもありません
パンはどれもありません
 レーズンは選ばれたフェスティバルにあり、その結果
レーズンは選ばれたフェスティバルにあり、その結果
 (37%-rule):
(37%-rule):
-

住所に関連する関連する封筒は、互いに独立して書かれています。それから見ずに、純粋に偶然に、文字は封筒に入れられます。適切な封筒に手紙がない可能性はどれくらいですか?
Eulerはこのタスクを解決し、1751年にエッセイ「Calcul da laprobabilitédansle jeu de rencontre」で公開しました。それは非常にうまくやります
 快適な、文字の数が大きくなっているときの確率の限界。
快適な、文字の数が大きくなっているときの確率の限界。
ハンターは1ショットのみが利用できます。それは群衆から鳩に言われています、その数
 彼は誰がランダムな順序で彼を通り過ぎて飛ぶことを知っています、偉大なものを撃ちます。どの戦略で最大のハトを作る可能性はありますか?この鳩の問題は、アメリカの数学者ハーバート・ロビンズ(*1915)によって策定されました。同じ決定 – 制作の問題は、N申請者(秘書問題)および同様の衣服で最高の従業員を雇用するときにも存在します。解決策:最適な戦略は、最初にです
彼は誰がランダムな順序で彼を通り過ぎて飛ぶことを知っています、偉大なものを撃ちます。どの戦略で最大のハトを作る可能性はありますか?この鳩の問題は、アメリカの数学者ハーバート・ロビンズ(*1915)によって策定されました。同じ決定 – 制作の問題は、N申請者(秘書問題)および同様の衣服で最高の従業員を雇用するときにも存在します。解決策:最適な戦略は、最初にです
 聴覚障がい
聴覚障がい
 飛び回ってから、それまでに大きいものが飛んでいない場合は、これまでよりも大きい、または最後の鳩を撃ちます。最大の鳩を捕まえる可能性は、この最適な戦略にほぼ存在します
飛び回ってから、それまでに大きいものが飛んでいない場合は、これまでよりも大きい、または最後の鳩を撃ちます。最大の鳩を捕まえる可能性は、この最適な戦略にほぼ存在します
 Nに関係なく、小さすぎてはなりません。もし私達
Nに関係なく、小さすぎてはなりません。もし私達
 の推定値として
の推定値として
 選択してから、次を続けます。
選択してから、次を続けます。
 。したがって、27匹の鳩で10を飛ばすだけです。できることは驚くべきことです
。したがって、27匹の鳩で10を飛ばすだけです。できることは驚くべきことです
 すべてのケースでは、目的の最適ソリューションを受け取りません。 [最初に30]
すべてのケースでは、目的の最適ソリューションを受け取りません。 [最初に30]
ポアソンでは、指数および正規分布
 他のサイズに加えて分布を説明するために使用されます。
他のサイズに加えて分布を説明するために使用されます。
Eulersche番号は、数学のさまざまな重要な場所に表示されます。
Eulersche数は、差分計算でも発生します。ポイントで
 最大関数です
最大関数です
 。さらに、場所があります
。さらに、場所があります
 関数の最小
関数の最小
 。これは、派生関数を使用して表示できます。
。これは、派生関数を使用して表示できます。
1850年のCrelles Journalの最も幸運なボリュームで、スイスの数学者Jakob Steinerは Eulerschen番号
 、 何
、 何
 極度の価値タスクの解決策として。シュタイナーはその数を示しました
極度の価値タスクの解決策として。シュタイナーはその数を示しました
 それは、ルートを引くときに最大のルートを提供する明らかに特定の正の実数として特徴付けられます。シュタイナーは文字通り次のように書いています:「各数値がそれ自体を根本的に根本的に介して、その数は最大のルートを付与します。」 [32]
それは、ルートを引くときに最大のルートを提供する明らかに特定の正の実数として特徴付けられます。シュタイナーは文字通り次のように書いています:「各数値がそれ自体を根本的に根本的に介して、その数は最大のルートを付与します。」 [32]
シュタイナーは、機能のために疑問を扱っています
-
![{displaystyle fcolon (0,infty )to (0,infty ),;xmapsto f(x)={sqrt[{x}]{x}}=x^{frac {1}{x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4063ce8d3cb0bd8e8e924fb9ad71d37de21cde0)
グローバルな最大値が存在し、どのように決定されるか。彼の声明は、それが存在し、それはで受け入れられているということです
 。
。
彼の本で 数学の勝利 HeinrichDörrieは、この極端な価値のタスクに対する基本的なソリューションを提供します。彼のアプローチは、実際の指数関数に関する次の真の声明に基づいています。
-

 すべての実数について続きます
すべての実数について続きます

-


 サイクリングによって [33] [34]
サイクリングによって [33] [34]
-
![{sqrt[ {e}]{e}}>{sqrt[ {x}]{x}}.”></span></dd>
</dl>
<p>番号の場合 <span class=](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab342b663cfdd9c7011e0a6b478c5c1bfd3afa1e)
 そして、それから派生した変数のさまざまな近似があります。だからチャールズ・ヘルミスは次の壊れた列を見つけました:
そして、それから派生した変数のさまざまな近似があります。だからチャールズ・ヘルミスは次の壊れた列を見つけました:
-

-

ここで、最初の休憩は0.0003%未満で死亡します
 ab。 [35]
ab。 [35]
3桁のフィギュア領域における最適な破損のスケール、すなわち最適なブレーク – イン
 と
と
 、 は
、 は
-
 。 [36]
。 [36]
ただし、この近似は、分母が最大3桁であることを要求するという意味での最良の和解ではありません。この意味でのもの 最高の破損 ユーラー数のチェーンブレイク開発の近似の9番目の骨折です。
-

また、近似ブレークから
 チェーンブレイキング開発に属する(上記参照)
チェーンブレイキング開発に属する(上記参照)
 そしてそれから派生したサイズ。これらを使用すると、任意の数の数字でオイラー番号の中で最高の休憩を見つけることができます。たとえば、5桁のフィギュアエリアでは、骨折の最高の休憩
そしてそれから派生したサイズ。これらを使用すると、任意の数の数字でオイラー番号の中で最高の休憩を見つけることができます。たとえば、5桁のフィギュアエリアでは、骨折の最高の休憩
-
 、
、
これは、チャールズ・ヘルミスが5桁の数の領域に見られるオイラーシュの数にまだ最適ではなかったことを示しています。
同様に、たとえば、C。D。オールズは近似を通してそれを示しました
-

Eulersche番号の場合、別の改善、つまり
-
 、
、
達成されることです。 [37]
全体として、通常のチェーンの破損から生じるオイラー数の最良の近似骨折の結果は、次のように始まります。 [38]
-
![{displaystyle {frac {p_{0}}{q_{0}}}=[2]={frac {2}{1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/03381f45a716a9bee38be402cff93ec440495a0a)
-
![{displaystyle {frac {p_{1}}{q_{1}}}=[2;1]={frac {3}{1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2316072a3b1365a6af9308370d7f5fd17be5e280)
-
![{displaystyle {frac {p_{2}}{q_{2}}}=[2;1,2]={frac {8}{3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/530494408d4f8555d5e5f2af1b59a82d06215fb0)
-
![{displaystyle {frac {p_{3}}{q_{3}}}=[2;1,2,1]={frac {11}{4}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eab8069ddc3e62296dc99022213d9e582823bbf9)
-
![{displaystyle {frac {p_{4}}{q_{4}}}=[2;1,2,1,1]={frac {19}{7}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0adc6df995e9f7668119e1ae09b5ebbe236c159e)
-
![{displaystyle {frac {p_{5}}{q_{5}}}=[2;1,2,1,1,4]={frac {87}{32}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c18e5f10931ca229a1ed97c6afc28e7f0498dbe)
-
![{displaystyle {frac {p_{6}}{q_{6}}}=[2;1,2,1,1,4,1]={frac {106}{39}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af6c1588826bc655dc5fd8f4173a8d0b412a7166)
-
![{displaystyle {frac {p_{7}}{q_{7}}}=[2;1,2,1,1,4,1,1]={frac {193}{71}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e969fea3e9db452e029be94ddd6e30f70745d67)
-
![{displaystyle {frac {p_{8}}{q_{8}}}=[2;1,2,1,1,4,1,1,6]={frac {1264}{465}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/977e9e0d8aa3ef1a10aa970110e67f87a479db07)
-
![{displaystyle {frac {p_{9}}{q_{9}}}=[2;1,2,1,1,4,1,1,6,1]={frac {1457}{536}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40a12b9ad513d0fbb72009763ad8547ac2a2f068)
-
![{displaystyle {frac {p_{10}}{q_{10}}}=[2;1,2,1,1,4,1,1,6,1,1]={frac {2721}{1001}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/219a5349e9f2e5a34461e50a54ba857ea469fa99)
-
![{displaystyle {frac {p_{11}}{q_{11}}}=[2;1,2,1,1,4,1,1,6,1,1,8]={frac {23225}{8544}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4cc6729ac076f4a520ed5f42d63b880fc82db8ba)
-

-
![{displaystyle {frac {p_{20}}{q_{20}}}=[2;1,2,1,1,4,1,1,6,1,1,8,1,1,10,1,1,12,1,1,14]={frac {410105312}{150869313}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b445d61ff55e58a2157d5baab2371fd7960d4f07)
-

小数点以下の場所を計算するには、通常、ラインディスプレイは
-

すぐに収束したと評価しました。循環エラーが結果を偽造しないように、実装するときに長い数の算術が重要です。この式にも基づいているが、複雑な実装を必要としない手順は、小数点以下の場所を計算するための液滴アルゴリズムです
 、A。H。J.セールファック。 [39]
、A。H。J.セールファック。 [39]
井戸の数の開発 – の10進数の場所

| データム |
番号 |
数学者 |
| 1748 |
23 |
レオンハルトオイラー [40] |
| 1853 |
137 |
ウィリアムシャンクス |
| 1871年 |
205 |
ウィリアムシャンクス |
| 1884年 |
346 |
J.マーカス・ブールマン |
| 1946年 |
808 |
? |
| 1949年 |
2.010 |
ジョン・フォン・ノイマン(エニアックで計算) |
| 1961年 |
100.265 |
ダニエル・シャンクスとジョン・レンチ |
| 1981年 |
116,000 |
Steve Wozniak(Apple IIを使用して計算) |
| 1994年 |
10,000,000 |
ロバート・ネミロフとジェリー・ボネル |
| 1997年5月 |
18.199.978 |
パトリック・デミチェル |
| 1997年8月 |
20,000,000 |
Biger’s Slicker |
| 1997年9月 |
50,000.817 |
パトリック・デミチェル |
| 1999年2月 |
200,000.579 |
セバスチャン・フェネロウキ |
| 1999年10月 |
869.894.101 |
セバスチャン・フェネロウキ |
| 21. 1999年11月 |
1,250,000,000 |
Xavier Gourdon |
| 2000年7月10日 |
2,147,483,648 |
Shigeru CondoとXavier Gourdon |
| 2000年7月16日 |
3.221.225.472 |
Colin Martin und Xavier Gourdon |
| 2. 2000年8月 |
6,442,450,944 |
Shigeru CondoとXavier Gourdon |
| 16. 2000年8月 |
12,884,901,000 |
Shigeru CondoとXavier Gourdon |
| 21. 2003年8月 |
25,100,000,000 |
Shigeru CondoとXavier Gourdon |
| 18. 2003年9月 |
50,100,000,000 |
Shigeru CondoとXavier Gourdon |
| 27. 2007年4月 |
100,000,000,000 |
Shigeru nodo Ud Steve Pagliarulo |
| 6. 2009年5月 |
200,000,000,000 |
Shigeru nodo Ud Steve Pagliarulo |
| 2010年2月20日 |
500,000,000,000 |
アレクサンダー・イー [41] |
| 2010年7月5日 |
1,000,000,000,000,000 |
Shigeru Kondo [41] |
| 24. 2015年6月 |
1,400,000,000,000,000 |
エリー・ヘバート [41] |
| 2016年2月14日 |
1,500,000,000,000 |
ロン・ワトキンス [41] |
| 29. 2016年5月 |
2,500,000,000,000 |
「Yoyo」 – 統一計算 [41] |
| 29. 2016年8月 |
5,000,000,000,000 |
ロン・ワトキンス [41] |
| 2019年1月3日 |
8,000,000,000,000 |
ジェラルド・ホフマン [41] |
| 2020年7月11日 |
12,000,000,000,000 |
デビッド・クリスル [41] |
| 22. 2020年11月 |
31.415.926.535.897 |
デビッド・クリスル [41] |
テレビシリーズで シンプソンズ そして彼らの後継シリーズ Futurama 多くの数学的参照があり、いくつかはオイラーの数も持っています
 そして、フクロウ。 [42]
そして、フクロウ。 [42]
1995年にテレビシリーズで付与されました ファイルX- FBIの怖いケース 番号シリーズ2-7-1-8-2-8 Secret Archiveへの2つのFBIエージェントアクセス。オイラーの数字ではなく、ネイピアの話がありました。 [43]
- ブライアン・J・マッカルティン: E:すべてのマスター。 数学的インテリゲンサー、2006年第28巻、No。2、pp。10–21。この記事はチャウブネット賞を受賞しました。 mathdl.mara.org
- ハインリッヒ・ドーリー: 数学の勝利。数千年の数千年の数百年の有名な問題 。第5版。 Physica-verlag、Würzburg1958。
- Leonhard Euler: 無限の分析の紹介 。の最初の部分 分析の紹介 。 Springer Verlag、ベルリン /ハイデルベルク /ニューヨーク1983、ISBN 3-540-12218-4( MR0715928 – ベルリン1885版の復刻版)。
- エルンストヘイラー、ゲルハルトワナー: 歴史的発展の分析 。 Springer-Verlag、Berlin、Heidelberg 2011、ISBN 978-3-642-13766-2。
- Konrad Knopp: 無限行の理論と適用 (= 数学科学の基本的な教え 。 バンド 2 )。 5番目、修正版。 Springer Verlag、ベルリン /Göttingen / Heidelberg / New York 1964、ISBN 3-540-03138-3( MR0183997 )。
- だからマア: E:数の物語 。プリンストン大学出版局、プリンストン1994、ISBN 978-0-691-14134-3。
- だからマア: 番号E:歴史と物語 。 BirkhäuserVerlag、Basel(を含む)1996、ISBN 3-7643-5093-8。
- C. D.オールズ: eの単純な継続的な画分拡大 。の: アメリカの数学毎月 。 バンド 77 、1971年、 S. 968–974 。
- Oskar Perron: 不合理な数 。第2版(ベルリン、1939年)の再版。 4.回避および補足。 Walter de Gruyter Verlag、Berlin 2011、ISBN 978-3-11-083604-2、doi: 10.1515/9783110836042.fm 。
- Oskar Perron: チェーンブレイクの教育II:分析機能と理論的チェーンブレイク 。 3番目、改善、およびエディションを通じて、Stuttgart 1957の再版の復刻版。4。全体と補足。 Teubner Verlag、Stuttgart 1977、ISBN 3-519-02022-X。
- J.シュタイナー: 各番号の部品または夏の最大の産物について 。の: 純粋および応用数学のためのジャーナル 。 バンド 40 、1850、 S. 208 ( gdz.sub.uni-goettingen.de )。
- デビッドウェルズ: 数字の辞書。博士の英語からKlaus Volkert 。オリジナルタイトル:好奇心and盛で興味深い数字のペンギン辞書。 Fischer Taschenbuch Verlag、Frankfurt/Main 1990、ISBN 3-596-10135-2。
- ↑ 結果 A001113 OEISで
- ↑ 注:eulersche番号はです いいえ オイラー・マシェロニ定数と同一
 、一部のソースでは、同様のサウンド名があります Eulersche Constant もっている。
、一部のソースでは、同様のサウンド名があります Eulersche Constant もっている。
- ↑ 楽しい休日 – e-day
- ↑ オイラー: はじめに…(§122) 。 S. 226–227 。
- ↑ オイラー: はじめに…(§§123,125) 。 S. 91–94 。
- ↑ a b 芽: 理論と適用…(§9) 。 S. 84 。
- ↑ ロジャー・B・ネルセン: 言葉のない証拠 、ドイツ語版Nicola Oswald、Springer Spektrum、Springer-Verlag Berlin Heidelberg 2016、ISBN 978-3-662-50330-0、178ページ
- ↑ H.wußing: 数学の歴史に関する講義。 Veb Deutscher Verlag Der Sciences、Berlin 1979、p。130。
- ↑ ピーター・メーダー: 数学には歴史があります。 Metzler Verlag、Hanover、1992、ISBN 3-8156-3363-X、pp。86–87。
- ↑ Otto Toeplitz: 無限のIMAL計算の開発。 Scientific Book Society、Darmstadt 1972、ISBN 3-534-06008-3、pp。25–27。
- ↑ Toeplitz、S。53–55。
- ↑ Toeplitz、S。91。
- ↑ R. P.バーン:Alphonse Antonio de Sarasa and Logarithms、Mathematica 28:1(2001) –
- ↑ ステファンクラウス: 発見の歴史と特別な番号の例外的な位置:
 (PDF; 211 kb)。の: 数学の教え、 1999、Vol.II、2、S。105–118。
(PDF; 211 kb)。の: 数学の教え、 1999、Vol.II、2、S。105–118。
- ↑ https://leibniz.uni-giettingen.de/files/pdf/leibniz-edition-iii-5.pdf 、ここで、たとえば、手紙番号6
- ↑ http://elerarchive.mara.org 、P。58: “…(e denotat hic numerum、cujus対数Hyperbolicus est = 1)、…”ドイツ語: “…(eは、双曲線[すなわち自然]対数が等しく1)を意味します)」
- ↑ https://scholarlycommons.pacific.edu/cgi/viewcontent.cgi?article=1852&context=euler-works 、「numero cujus対数ast unitas、e、qui est 2,7182817あたりのscribature est 2,7182817 …」(ドイツ語:「2,7182817 … … … … …」
- ↑ https://scholarlylycommons.pacific.edu/Eler-works/853/
- ↑ オイラー: はじめに…(§122) 。 S. 91 。 Eulerは書いています(Hermann Maserの翻訳による):
 常に文字
常に文字
 それを使用してください
それを使用してください
 自然または双曲線の対数の基礎は[…]を意味します。
自然または双曲線の対数の基礎は[…]を意味します。
 常に無限シリーズの合計
常に無限シリーズの合計
 説明。”
説明。”
- ↑ Hans F. Ebel、Claus Bliefert、Walter Greulich: 自然科学の執筆と出版 。第5版。 Wiley-VCH、Weinheim、ISBN 3-527-66027-5。
- ↑ パウロ・リベンボイム: 私の数字、私の友人:数の理論のハイライト。 Springer Textbook、2009、ISBN 978-3-540-87955-8、p。299。
- ↑ リチャードジョージストーンハム: 合理的な画分からの超越的な非liouvilleの正常数の一般的な算術構造 。 (PDF; 692 KB)。の: ACTA算術 、16、1970、S。239–253。
- ↑ スターリングフォーミュラ 。 (PDF; 76 kb)。 In:James Stirling: 微分の方法 。 1730、S。1。
- ↑ エルンストヘイラー、ゲルハルトワナー: 歴史的発展の分析。 2011年、S。41。
- ↑ ペロン: 不合理な数 。 S. 115 。
- ↑ オイラー、S。305。
- ↑ a b ペロン: チェーンの教育が壊れます 。 バンド ii 、 S. 19 。
- ↑ ペロン: チェーンの教育が壊れます 。 バンド ii 、 S. 157 。
- ↑ ID(3)への接続に注意してください!
- ↑ Gal Raayoni et al。: ラマヌジャンマシン:基本定数で自動的に生成された推測 。 arxiv: 1907.00205 、2019年7月23日の改訂版、2019年7月28日アクセス。
- ↑ P.メーダー、p。96/7
- ↑ 各番号の部品または夏の最大の産物について 。の: 純粋および応用数学のためのジャーナル 。 バンド 40 、1850、 S. 208 。
- ↑ Dörrie、S。358。
- ↑ また、微分計算で曲線ディスカッションで使用される方法でこのタスクを解決することもできます。
- ↑ マール、S。185。
- ↑ ウェルズ、S。46。
- ↑ オールズ: eの単純な継続的な画分拡大 。の: Amer。算数。毎月 。 1971年、 S. 973 。
- ↑ エピソードを参照してください A007676 カウンターとエピソードのOEISで A0A007677 分母のOEISで。
- ↑ A. H. J.セール: 多くの有意な数字からEの計算 。の: コンピュータージャーナル 。 バンド 11 、 いいえ。 2 、1968年8月、 S. 229–230 、doi: 10.1093/comjnl/11.2.229 。
- ↑ レオンハルド・エウレロ: 無限の分析の紹介。 第1巻、Marcus-Michaelis Bousquet and Socii、Lausannæ1748(ラテン語; “2,7182845904523536028” books.google.de S. 90)。
- ↑ a b c d そうです f g h 私 アレクサンダー・J・イー: そうです。 の: numberworld.org。 2020年12月5日、 2020年12月12日に取得 (英語)。
- ↑ サイモン・シン: ホーマーの最後の文。 DTV、Munich 2013、ISBN 978-3-423-34847-8。
- ↑ 卒業論文: 番号e。 (PDF; 1,1 MB)、S。6。
 記載されているのは、分析全体と数学のすべてのサブエリア、特に差動および積分計算でも、石依存症(組み合わせ、正規分布)において中心的な役割を果たしている定数です。あなたの数値はです
記載されているのは、分析全体と数学のすべてのサブエリア、特に差動および積分計算でも、石依存症(組み合わせ、正規分布)において中心的な役割を果たしている定数です。あなたの数値はです 


 入っています
入っています  の教員
の教員  、その場合
、その場合 
 の自然数
の自然数  それまで
それまで  定義されています。
定義されています。  と
と  書かれる:
書かれる: 

 ポイントで
ポイントで  : [6]
: [6] 











 したがって
したがって  Ferdinand von Lindemann 1882)によると、2つの自然数(代数方程式の解決策としても)の休憩としてではなく、その結果、無限の非周期フラグメント開発があります。の不合理性
Ferdinand von Lindemann 1882)によると、2つの自然数(代数方程式の解決策としても)の休憩としてではなく、その結果、無限の非周期フラグメント開発があります。の不合理性 
 複雑な数と回路の数
複雑な数と回路の数 



 間隔で
間隔で ![{displaystyle [1,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8771aaef108f3cf1381367f4874c74ae7b5e9aa5) まったく同じ
まったく同じ 
![e = lim_{ntoinfty} frac{n}{sqrt[n]{n!}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/310afedad5e855a28eb0d1b232a29031bd682548)

![e = lim_{n to infty} (sqrt[n]{n})^{pi(n)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d630cbe58c254c4dc64710f9a81dacddc9897d8)
![e = lim_{n to infty} sqrt[n]{n#}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a49850b48669d471e09b151b3ef18f0a81e87344)
 素数関数とシンボル
素数関数とシンボル  数字の原始
数字の原始  意味。
意味。 ![e=sqrt[1]{frac{2}{1}}cdotsqrt[2]{frac{4}{3}}cdotsqrt[4]{frac{6cdot 8}{5cdot 7}}cdotsqrt[8]{frac{10cdot 12cdot 14cdot 16}{9cdot 11cdot 13cdot 15}}cdots](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e598bf5c258b6349e3cd7adfe125b915e77dbd4)
![{displaystyle (1){begin{aligned}e&=[2;1,2,1,1,4,1,1,6,1,1,8,1,1,10,1,dotsc ]\&=2+{cfrac {1}{1+{cfrac {1}{2+{cfrac {1}{1+{cfrac {1}{1+{cfrac {1}{4+{cfrac {1}{1+{cfrac {1}{1+{cfrac {1}{6+dotsb }}}}}}}}}}}}}}}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5ec3169e1a05da55f303dc18cd87060421a9b8a)
![{displaystyle (2){begin{aligned}{frac {e+1}{e-1}}&=[2;6,10,14,dotsc ]\&={2+{cfrac {1}{6+{cfrac {1}{10+{cfrac {1}{14+{cfrac {1}{;,ddots }}}}}}}}}\&approx 2{,}1639534137386end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5fa822639e5939f4fa0b49836a70f10e4470da43)
 :
: ![{displaystyle (3){begin{aligned}{coth {frac {1}{k}}}&={frac {e^{frac {2}{k}}+1}{e^{frac {2}{k}}-1}}\&=[k;3k,5k,7k,dots ]\&={k+{cfrac {1}{3k+{cfrac {1}{5k+{cfrac {1}{7k+{cfrac {1}{;,ddots }}}}}}}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12af66797cccd4b577eb60dc5ff4b0147a0a6cd2)










 1年当たり。来年の1月1日の彼が同じ条件で関心を生み出したとき、彼の信用はどれくらい大きいですか?
1年当たり。来年の1月1日の彼が同じ条件で関心を生み出したとき、彼の信用はどれくらい大きいですか?  後
後  首都
首都 
 と
と  利息追加料金が毎年行われる場合、または
利息追加料金が毎年行われる場合、または  利息追加料金の場合
利息追加料金の場合 
 、
、 
 あなたは得ます
あなたは得ます 
 それで
それで  (37%-rule):
(37%-rule): 
 快適な、文字の数が大きくなっているときの確率の限界。
快適な、文字の数が大きくなっているときの確率の限界。  飛び回ってから、それまでに大きいものが飛んでいない場合は、これまでよりも大きい、または最後の鳩を撃ちます。最大の鳩を捕まえる可能性は、この最適な戦略にほぼ存在します
飛び回ってから、それまでに大きいものが飛んでいない場合は、これまでよりも大きい、または最後の鳩を撃ちます。最大の鳩を捕まえる可能性は、この最適な戦略にほぼ存在します  の推定値として
の推定値として  。したがって、27匹の鳩で10を飛ばすだけです。できることは驚くべきことです
。したがって、27匹の鳩で10を飛ばすだけです。できることは驚くべきことです  すべてのケースでは、目的の最適ソリューションを受け取りません。 [最初に30]
すべてのケースでは、目的の最適ソリューションを受け取りません。 [最初に30]  。さらに、場所があります
。さらに、場所があります  関数の最小
関数の最小  。これは、派生関数を使用して表示できます。
。これは、派生関数を使用して表示できます。 ![{displaystyle fcolon (0,infty )to (0,infty ),;xmapsto f(x)={sqrt[{x}]{x}}=x^{frac {1}{x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4063ce8d3cb0bd8e8e924fb9ad71d37de21cde0)
 。
。 




![{sqrt[ {e}]{e}}>{sqrt[ {x}]{x}}.”></span></dd>
</dl>
<p>番号の場合 <span class=](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab342b663cfdd9c7011e0a6b478c5c1bfd3afa1e)


 と
と  、 は
、 は 




![{displaystyle {frac {p_{0}}{q_{0}}}=[2]={frac {2}{1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/03381f45a716a9bee38be402cff93ec440495a0a)
![{displaystyle {frac {p_{1}}{q_{1}}}=[2;1]={frac {3}{1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2316072a3b1365a6af9308370d7f5fd17be5e280)
![{displaystyle {frac {p_{2}}{q_{2}}}=[2;1,2]={frac {8}{3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/530494408d4f8555d5e5f2af1b59a82d06215fb0)
![{displaystyle {frac {p_{3}}{q_{3}}}=[2;1,2,1]={frac {11}{4}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eab8069ddc3e62296dc99022213d9e582823bbf9)
![{displaystyle {frac {p_{4}}{q_{4}}}=[2;1,2,1,1]={frac {19}{7}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0adc6df995e9f7668119e1ae09b5ebbe236c159e)
![{displaystyle {frac {p_{5}}{q_{5}}}=[2;1,2,1,1,4]={frac {87}{32}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c18e5f10931ca229a1ed97c6afc28e7f0498dbe)
![{displaystyle {frac {p_{6}}{q_{6}}}=[2;1,2,1,1,4,1]={frac {106}{39}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af6c1588826bc655dc5fd8f4173a8d0b412a7166)
![{displaystyle {frac {p_{7}}{q_{7}}}=[2;1,2,1,1,4,1,1]={frac {193}{71}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e969fea3e9db452e029be94ddd6e30f70745d67)
![{displaystyle {frac {p_{8}}{q_{8}}}=[2;1,2,1,1,4,1,1,6]={frac {1264}{465}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/977e9e0d8aa3ef1a10aa970110e67f87a479db07)
![{displaystyle {frac {p_{9}}{q_{9}}}=[2;1,2,1,1,4,1,1,6,1]={frac {1457}{536}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40a12b9ad513d0fbb72009763ad8547ac2a2f068)
![{displaystyle {frac {p_{10}}{q_{10}}}=[2;1,2,1,1,4,1,1,6,1,1]={frac {2721}{1001}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/219a5349e9f2e5a34461e50a54ba857ea469fa99)
![{displaystyle {frac {p_{11}}{q_{11}}}=[2;1,2,1,1,4,1,1,6,1,1,8]={frac {23225}{8544}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4cc6729ac076f4a520ed5f42d63b880fc82db8ba)

![{displaystyle {frac {p_{20}}{q_{20}}}=[2;1,2,1,1,4,1,1,6,1,1,8,1,1,10,1,1,12,1,1,14]={frac {410105312}{150869313}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b445d61ff55e58a2157d5baab2371fd7960d4f07)





Recent Comments