半径2/3の円の周りに円を回転させることにより、同じ腎性の構築
一 nephroide (aus altgriechischὁ腎臓 ホーネフロス 、「腎臓」、その形状に応じて)は代数曲線です。
ネフロイドは、半径で円を転がすことによって作成されます
 半径のある円の外側
半径のある円の外側
 。これは、腎症が上腺体のクラスに属していることを意味します。
。これは、腎症が上腺体のクラスに属していることを意味します。
は
 小さな(ローリング)円の半径と
小さな(ローリング)円の半径と
 大きな(固体)円の中心と半径、
大きな(固体)円の中心と半径、
 (小さな円の)ローラー角度とポイント
(小さな円の)ローラー角度とポイント
 出発点(写真を参照)、それがあなたが得る方法です
出発点(写真を参照)、それがあなたが得る方法です
-

-
 。
。
方程式にパラメーター表現を挿入します

それが関連する暗黙の表現であることを証明します。
- パラメーター表現の証明
パラメータープレゼンテーションの証拠は、複雑な数字とあなたの表現をガウセの数字レベルとしての助けを借りて簡単に主張できます。青い円の黒い円の転がり動きは、2つの回転の連続に分解できます。ポイントの回転
 (複雑な数)ゼロポイントの周り
(複雑な数)ゼロポイントの周り
 角度で
角度で
 の乗算を通じてです
の乗算を通じてです
 引き起こされた。
引き起こされた。
- 回転
 ポイントへ
ポイントへ
 角度の周り
角度の周り
 は
は
 。
。
- 回転
 ポイントへ
ポイントへ
 角度の周り
角度の周り
 は
は
 。
。
nephroidポイント
 ポイントを回転させることによって作成されます
ポイントを回転させることによって作成されます
 と
と
 と後続の回転
と後続の回転
 :
:
-
 。
。
これはこれに起因します
-

(式はなりました
 使用済み。フォーミュラコレクションの三角法を参照してください。)
使用済み。フォーミュラコレクションの三角法を参照してください。)
- 暗黙の表現の証明
と
 降伏した
降伏した
-

- 異なる方向
ヒントがy軸上にある場合:
パラメータープレゼンテーション:
-

方程式:
-

上記のネフロイドの場合
証拠は、パラメータープレゼンテーションを使用します
-

-

上記の腎臓とその派生
-

-

領域の面積と曲線長の式zを見つけることができます。 B.こちら。 [初め]
- 曲線長の証明
パラメーター化された曲線の長さの式で結果
-
 。
。
- 地域の証明(ライプニッツセクターの式)
-
-
![{displaystyle A=2cdot {tfrac {1}{2}}|int _{0}^{pi }[x{dot {y}}-y{dot {x}}];dvarphi |=cdots =24a^{2}int _{0}^{pi }sin ^{2}varphi ;dvarphi =12pi a^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de13ba263785d0122ca3e5cefc4e65addd140efa) 。
。
- 曲率半径の証明
-
-


円形の円の封筒としての腎臓
適用されます:
- 証拠
そうです
 円
円
 中心に
中心に
 そして半径
そして半径
 。必要な直径はX軸にあります(写真を参照)。円は次のとおりです。
。必要な直径はX軸にあります(写真を参照)。円は次のとおりです。
-

封筒の状態はです
-

nephroidポイントが期待されています
 2つの方程式
2つの方程式
 充足され、したがって円の封筒のポイント。
充足され、したがって円の封筒のポイント。

群衆の封筒としての腎臓:腎臓の接線は円の腱です。腱は、円形経路でポイントnとポイント3nの間を走行します。これは、3の倍数に対応するいくつかのステップに均等に分割されます。

直線の群衆の封筒としてのネフロイド:腎臓の接線は円の腱です
群衆に包まれたカーディオイドの生成と同様に、次のことがここに当てはまります。
- 円を描き、それを均等に共有しました
 ポイント(写真を参照)と継続的に番号。
ポイント(写真を参照)と継続的に番号。
- 腱を描く:
 。 (このように表現できます。腱の2番目のポイントは、三重速度で動きます。)
。 (このように表現できます。腱の2番目のポイントは、三重速度で動きます。)
- 封筒 このルートは腎臓です。
- 証拠
の三角式の式
 使用済み。請求書を簡単に保つために、Y軸のヒントを持つ腎臓の証明が導かれます。
使用済み。請求書を簡単に保つために、Y軸のヒントを持つ腎臓の証明が導かれます。
- 接線の方程式
- パラメータープレゼンテーションを使用して腎臓へ
-
 :
:
パラメーター表現から
最初に通常のベクトルを計算します
 。
。
接線の方程式
 その後:
その後:
-

ために
 ネフロイドにはその先端があり、そこでは接線がありません。ために
ネフロイドにはその先端があり、そこでは接線がありません。ために
 通り抜けてもらえますか
通り抜けてもらえますか
 分割して最終的に受信します
分割して最終的に受信します

- セカントの方程式
- 中心のある円に
 そして半径
そして半径
 :2つのポイントから2番目の方程式の場合
:2つのポイントから2番目の方程式の場合
 降伏:
降伏:
-

ために
 セカントがポイントの1つである場合。ために
セカントがポイントの1つである場合。ために
 通り抜けてもらえますか
通り抜けてもらえますか
 分割とsekantの方程式の結果:
分割とsekantの方程式の結果:

2つの角度
 意味が異なります(
意味が異なります(
 ローラー角の半分、
ローラー角の半分、
 セカンターが計算される円のパラメーターです)
セカンターが計算される円のパラメーターです)
 しかし、同じ結果。したがって、上記の各秒は腎臓の接線であり、
しかし、同じ結果。したがって、上記の各秒は腎臓の接線であり、
円の苛性としての腎臓:原理

半円の苛性としての腎臓
以前の考慮事項は、腎臓が半円のca産業として発生することの証拠も提供します。
- レベルの図に従って平行光線が反射的な半円に落ちた場合、反射光線は腎臓の接線です。 (セクションを参照:日常生活におけるネフロイド)
- 証拠
円(前のセクションのように)の中心とその半径はゼロポイントがありました
 。その後、円にはパラメータープレゼンテーションがあります
。その後、円にはパラメータープレゼンテーションがあります
-

円形ポイントの接線
 通常のベクトルがあります
通常のベクトルがあります
 。反射ビームは(図に従って)通常のベクトルでなければなりません
。反射ビームは(図に従って)通常のベクトルでなければなりません
 丸いポイントを介して
丸いポイントを介して
 行く。反射ビームは方程式とともに直線にあります
行く。反射ビームは方程式とともに直線にあります
-

これは、ポイントの前のセクションの腎臓の接線です
-

IS(上記参照)。

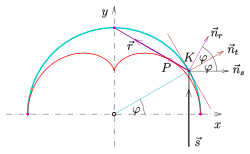
nephroid(赤)とその進化(緑)、
マゼンタ:ポイントP、その曲率中心M、および関連する曲率円
平らな曲線の進化は、この曲線のすべての曲率点の幾何学的な場所です。パラメーター化された曲線の場合
 曲率半径があります
曲率半径があります
 Evoluteにはパラメータープレゼンテーションがあります
Evoluteにはパラメータープレゼンテーションがあります
-

したがって
 適切なユニットは正常です。 (()
適切なユニットは正常です。 (()
 曲率の平均を指します。)
曲率の平均を指します。)
以下は、写真の腎臓に適用されます。
- 進化しました ネフロイドは再び腎臓で、半分の大きさです。
- 証拠
写真の腎臓(ヒントはy軸上にあります!)にはパラメーター表現があります
-

ユニットは正常です
-
 (上記を参照)
(上記を参照)
曲率の半径があります(上記参照)
-
 。
。
したがって、Evoluteにはパラメータープレゼンテーションがあります
-

-

これらの方程式は、半分の大きさで90度に変わった腎臓を表しています(写真とセクションを参照してください 腎臓の方程式 )。

青い円のニフロイド(赤)の反転(緑)
反射
-

中心のある円で
 そして半径
そして半径
 方程式でネフロイドを形成します
方程式でネフロイドを形成します
-

方程式のある曲線6度
-

from(写真を参照)。
光が凹状の円形反射表面の側面にある無限に遠い光源の側面に光が当てられた場合、光線の包みが腎臓の一部を形成します。したがって、「コーヒーカップCaustic」(Kaustik = Fuel Line)とも呼ばれることもあります。また、自転車の裸の縁が床の光を反映しているときに路上でそれらを見ることができます。日光が自転車のリムのシリンダーコートに並行してヒットするため、ヒューズは半分ネフロイドの形状を持つプロファイルを描いており、レベルの地下形状のネフロイドの一部をカットするようにします。
- ↑ Kurt Meyberg、Peter Vachenauer: より高い数学1。 Springs-Publising、1995、ISBN 3-540-59188-5、S。1948、.. 194、2008。
- D.アーガンブライト: スプレッドシート曲線と幾何学的構造の実用的なハンドブック。 CRC Press、1993、ISBN 0-8493-8938-0、S。54。
- F. Borceux: ジオメトリへの微分アプローチ:幾何学的三部作III。 Springer、2014、ISBN 978-3-319-01735-8、S。148。
- E. H.ロックウッド: 曲線の本。 ケンブリッジ大学出版局、1978年、ISBN 0-521-05585-7、S。7。











 半径のある円の外側
半径のある円の外側  。これは、腎症が上腺体のクラスに属していることを意味します。
。これは、腎症が上腺体のクラスに属していることを意味します。  大きな(固体)円の中心と半径、
大きな(固体)円の中心と半径、  (小さな円の)ローラー角度とポイント
(小さな円の)ローラー角度とポイント  出発点(写真を参照)、それがあなたが得る方法です
出発点(写真を参照)、それがあなたが得る方法です 


 (複雑な数)ゼロポイントの周り
(複雑な数)ゼロポイントの周り  角度で
角度で  の乗算を通じてです
の乗算を通じてです  引き起こされた。
引き起こされた。 




 ポイントを回転させることによって作成されます
ポイントを回転させることによって作成されます 

 使用済み。フォーミュラコレクションの三角法を参照してください。)
使用済み。フォーミュラコレクションの三角法を参照してください。)  降伏した
降伏した 







![{displaystyle A=2cdot {tfrac {1}{2}}|int _{0}^{pi }[x{dot {y}}-y{dot {x}}];dvarphi |=cdots =24a^{2}int _{0}^{pi }sin ^{2}varphi ;dvarphi =12pi a^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de13ba263785d0122ca3e5cefc4e65addd140efa)

 円
円  中心に
中心に  そして半径
そして半径 

 2つの方程式
2つの方程式  充足され、したがって円の封筒のポイント。
充足され、したがって円の封筒のポイント。 

 使用済み。請求書を簡単に保つために、Y軸のヒントを持つ腎臓の証明が導かれます。
使用済み。請求書を簡単に保つために、Y軸のヒントを持つ腎臓の証明が導かれます。 
 。
。  その後:
その後: 
 ネフロイドにはその先端があり、そこでは接線がありません。ために
ネフロイドにはその先端があり、そこでは接線がありません。ために  通り抜けてもらえますか
通り抜けてもらえますか  分割して最終的に受信します
分割して最終的に受信します 



 セカントがポイントの1つである場合。ために
セカントがポイントの1つである場合。ために  通り抜けてもらえますか
通り抜けてもらえますか  分割とsekantの方程式の結果:
分割とsekantの方程式の結果: 
 意味が異なります(
意味が異なります(  セカンターが計算される円のパラメーターです)
セカンターが計算される円のパラメーターです)  しかし、同じ結果。したがって、上記の各秒は腎臓の接線であり、
しかし、同じ結果。したがって、上記の各秒は腎臓の接線であり、 
 通常のベクトルがあります
通常のベクトルがあります  。反射ビームは(図に従って)通常のベクトルでなければなりません
。反射ビームは(図に従って)通常のベクトルでなければなりません  丸いポイントを介して
丸いポイントを介して  行く。反射ビームは方程式とともに直線にあります
行く。反射ビームは方程式とともに直線にあります 

 曲率半径があります
曲率半径があります  Evoluteにはパラメータープレゼンテーションがあります
Evoluteにはパラメータープレゼンテーションがあります 
 適切なユニットは正常です。 (()
適切なユニットは正常です。 (() 







Recent Comments