Luftige Funktion – Wikipedia

In den Naturwissenschaften ist die Luftige Funktion (oder Luftige Funktion der ersten Art) Ai (x) ist eine Sonderfunktion, die nach dem britischen Astronomen George Biddell Airy (1801–1892) benannt ist. Die Funktion Ai (x) und die zugehörige Funktion Bi(x)sind linear unabhängige Lösungen der Differentialgleichung

${ displaystyle { frac {d ^ {2} y} {dx ^ {2}}} – xy = 0, , !}$

bekannt als Luftige Gleichung oder der Stokes-Gleichung. Dies ist die einfachste lineare Differentialgleichung zweiter Ordnung mit einem Wendepunkt (ein Punkt, an dem sich der Charakter der Lösungen von oszillierend zu exponentiell ändert).

Die Airy-Funktion ist die Lösung der zeitunabhängigen Schrödinger-Gleichung für ein Teilchen, das in einer dreieckigen Potentialwanne eingeschlossen ist, und für ein Teilchen in einem eindimensionalen Feld mit konstanter Kraft. Aus dem gleichen Grund dient es auch dazu, einheitliche semiklassische Approximationen nahe einem Wendepunkt in der WKB-Approximation bereitzustellen, wenn das Potential durch eine lineare Positionsfunktion lokal approximiert werden kann. Die dreieckige Potentialtopflösung ist direkt relevant für das Verständnis von Elektronen, die in Halbleiter-Heteroübergängen gefangen sind.

Die Airy-Funktion liegt auch der Form der Intensität in der Nähe eines optisch gerichteten Ätzmittels wie dem des Regenbogens zugrunde. Historisch gesehen war dies das mathematische Problem, das Airy dazu veranlasste, diese spezielle Funktion zu entwickeln.

Eine andere Funktion, die auch nach Airy benannt ist, ist in der Mikroskopie und Astronomie wichtig. Es beschreibt das Muster aufgrund von Beugung und Interferenz, das von einer Punktlichtquelle erzeugt wird (eine, die viel kleiner als die Auflösungsgrenze eines Mikroskops oder Teleskops ist).

Definitionen[edit]

Handlung von Ai (x) in rot und Bi (x) in Blau

Für reale Werte von xkann die Airy-Funktion der ersten Art durch das falsche Riemann-Integral definiert werden:

${ displaystyle operatorname {Ai} (x) = { dfrac {1} { pi}} int _ {0} ^ { infty} cos left ({ dfrac {t ^ {3}} { 3}} + xt right) , dt equiv { dfrac {1} { pi}} lim _ {b to infty} int _ {0} ^ {b} cos left ({ dfrac {t ^ {3}} {3}} + xt right) , dt,}$

was durch Dirichlet-Test konvergiert. Für jede reelle Zahl

es gibt eine positive reelle Zahl

so dass Funktion

nimmt zu, ist unbegrenzt und konvex mit kontinuierlicher und unbegrenzter Ableitung des Intervalls

. The convergence of the integral on this interval can be proven by Dirichlet’s test after substitution

.

y = Ai(x) satisfies the Airy equation

${displaystyle y”-xy=0.}$

This equation has two linearly independent solutions.
Up to scalar multiplication, Ai(x) is the solution subject to the condition y → 0 as x → ∞.
The standard choice for the other solution is the Airy function of the second kind, denoted Bi(x). It is defined as the solution with the same amplitude of oscillation as Ai(x) as x → −∞ which differs in phase by π/2:

${ displaystyle operatorname {Bi} (x) = { frac {1} { pi}} int _ {0} ^ { infty} left[exp left(-{tfrac {t^{3}}{3}}+xtright)+sin left({tfrac {t^{3}}{3}}+xtright),right]dt.}$

Eigenschaften[edit]

Die Werte von Ai (x) und Bi (x) und deren Derivate bei x = 0 sind gegeben durch

${ displaystyle { begin {align} operatorname {Ai} (0) & {} = { frac {1} {3 ^ { frac {2} {3}} Gamma ({ tfrac {2} { 3}})}}, & quad operatorname {Ai} ‘(0) & {} = – { frac {1} {3 ^ { frac {1} {3}} Gamma ({ tfrac { 1} {3}})}}, \ operatorname {Bi} (0) & {} = { frac {1} {3 ^ { frac {1} {6}} Gamma ({ tfrac { 2} {3}})}}, & quad operatorname {Bi} ‘(0) & {} = { frac {3 ^ { frac {1} {6}}} { Gamma ({ tfrac {1} {3}})}}. End {align}}}$

Hier bezeichnet Γ die Gammafunktion. Daraus folgt, dass der Wronskianer von Ai (x) und Bi (x) ist 1 / π.

Wann x ist positiv, Ai (x) ist positiv, konvex und nimmt exponentiell auf Null ab, während Bi (x) ist positiv, konvex und nimmt exponentiell zu. Wann x ist negativ, Ai (x) und Bi (x) schwingen um Null mit immer größerer Frequenz und immer kleiner werdender Amplitude. Dies wird durch die folgenden asymptotischen Formeln für die Airy-Funktionen unterstützt.

Die Airy-Funktionen sind orthogonal^[1] in dem Sinne, dass

${ displaystyle int _ {- infty} ^ { infty} operatorname {Ai} (t + x) operatorname {Ai} (t + y) dt = delta (xy)}$

wieder mit einem falschen Riemannschen Integral.

Asymptotische Formeln[edit]

Ai (blau) und sinusförmige / exponentielle asymptotische Form von Ai (Magenta)

Bi (blau) und sinusförmige / exponentielle asymptotische Form von Bi (magenta)

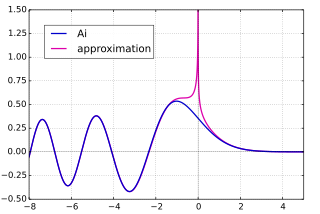
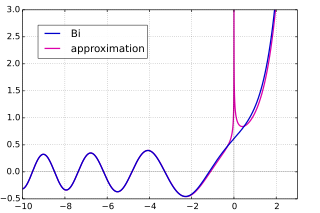
Wie unten erläutert, können die Airy-Funktionen auf die komplexe Ebene erweitert werden, wodurch ganze Funktionen erhalten werden. Das asymptotische Verhalten des Airy funktioniert als | z | geht mit einem konstanten Wert von arg (ins Unendliche)z) hängt von arg ab (z): Dies nennt man das Stokes-Phänomen. Für | arg (z) | <π wir haben die folgende asymptotische Formel für Ai (z):^[2]

${ displaystyle operatorname {Ai} (z) sim { dfrac {e ^ {- { frac {2} {3}} z ^ { frac {3} {2}}} {2 { sqrt { pi}} , z ^ { frac {1} {4}}}} left[sum _{n=0}^{infty }{dfrac {(-1)^{n}Gamma (n+{frac {5}{6}})Gamma (n+{frac {1}{6}})left({frac {3}{4}}right)^{n}}{2pi n!z^{3n/2}}}right].}$

und eine ähnliche für Bi (z), aber nur anwendbar, wenn | arg (z) | <π / 3:

${ displaystyle operatorname {Bi} (z) sim { frac {e ^ {{ frac {2} {3}} z ^ { frac {3} {2}}} {{ sqrt { pi}} , z ^ { frac {1} {4}}}} left[sum _{n=0}^{infty }{dfrac {Gamma (n+{frac {5}{6}})Gamma (n+{frac {1}{6}})left({frac {3}{4}}right)^{n}}{2pi n!z^{3n/2}}}right].}$

Eine genauere Formel für Ai (z) und eine Formel für Bi (z) wenn π / 3 <| arg (z) | <π oder äquivalent für Ai (-z) und Bi (-z) wenn | arg (z) | <2π / 3, aber nicht Null, sind:^[2][3]

${ displaystyle { begin {align} operatorname {Ai} (-z) sim & {} { frac { sin left ({ frac {2} {3}} z ^ { frac {3} {2}} + { frac { pi} {4}} right)} {{ sqrt { pi}} , z ^ { frac {1} {4}}} left[sum _{n=0}^{infty }{dfrac {(-1)^{n}Gamma (2n+{frac {5}{6}})Gamma (2n+{frac {1}{6}})left({frac {3}{4}}right)^{2n}}{2pi (2n)!z^{3n}}}right]\[6pt]& {} – { frac { cos left ({ frac {2} {3}} z ^ { frac {3} {2}} + { frac { pi} {4}} right) } {{ sqrt { pi}} , z ^ { frac {1} {4}}}} left[sum _{n=0}^{infty }{dfrac {(-1)^{n}Gamma (2n+{frac {11}{6}})Gamma (2n+{frac {7}{6}})left({frac {3}{4}}right)^{2n+1}}{2pi (2n+1)!z^{3n+3/2}}}right]\[6pt] operatorname {Bi} (-z) sim & {} { frac { cos left ({ frac {2} {3}} z ^ { frac {3} {2}} + { frac { pi} {4}} right)} {{ sqrt { pi}} , z ^ { frac {1} {4}}}} left[sum _{n=0}^{infty }{dfrac {(-1)^{n}Gamma (2n+{frac {5}{6}})Gamma (2n+{frac {1}{6}})left({frac {3}{4}}right)^{2n}}{2pi (2n)!z^{3n}}}right]\[6pt]& {} + { frac { sin left ({ frac {2} {3}} z ^ { frac {3} {2}} + { frac { pi} {4}} right) } {{ sqrt { pi}} , z ^ { frac {1} {4}}}} left[sum _{n=0}^{infty }{dfrac {(-1)^{n}Gamma (2n+{frac {11}{6}})Gamma (2n+{frac {7}{6}})left({frac {3}{4}}right)^{2n+1}}{2pi (2n+1)!z^{3n+3/2}}}right]. end {align}}}$

Wenn | arg (z) | = 0 Dies sind gute Näherungen, aber nicht asymptotisch, da das Verhältnis zwischen Ai (-z) oder Bi (-z) und die obige Näherung geht gegen unendlich, wenn der Sinus oder Cosinus auf Null geht. Asymptotische Erweiterungen für diese Grenzwerte sind ebenfalls verfügbar. Diese sind in (Abramowitz und Stegun, 1954) und (Olver, 1974) aufgeführt.

Man kann auch asymptotische Ausdrücke für die Derivate Ai ‘(z) und Bi’ (z) erhalten. Ähnlich wie zuvor, wenn | arg (z) | <π:^[3]

Wenn | arg (z) | <π / 3 ist, haben wir:^[3]

Ebenso ein Ausdruck für Ai ‘(-z) und Bi ‘(-z) wenn | arg (z) | <2π / 3, aber nicht Null, sind^[3]

Komplexe Argumente[edit]

Wir können die Definition der Airy-Funktion auf die komplexe Ebene erweitern durch

${ displaystyle operatorname {Ai} (z) = { frac {1} {2 pi i}} int _ {C} exp left ({ tfrac {t ^ {3}} {3}} -zt right) , dt,}$

wo das Integral über einem Pfad liegt C. beginnend am Punkt im Unendlichen mit dem Argument −π / 3 und endend am Punkt im Unendlichen mit dem Argument π / 3. Alternativ können wir die Differentialgleichung verwenden y” – xy = 0, um Ai zu erweitern (x) und Bi (x) zu ganzen Funktionen auf der komplexen Ebene.

Die asymptotische Formel für Ai (x) ist in der komplexen Ebene weiterhin gültig, wenn der Hauptwert von x^2/3 genommen wird und x ist von der negativen realen Achse weg begrenzt. Die Formel für Bi (x) ist gültig vorausgesetzt x ist in der Branche {x ∈ C. : | arg (x) | <(π / 3) −δ} für ein positives δ. Schließlich die Formeln für Ai (-x) und Bi (-x) sind gültig wenn x ist in der Branche {x ∈ C. : | arg (x) | <(2π / 3) −δ}.

Aus dem asymptotischen Verhalten der Airy-Funktionen folgt, dass beide Ai (x) und Bi (x) haben eine Unendlichkeit von Nullen auf der negativen reellen Achse. Die Funktion Ai (x) hat keine anderen Nullen in der komplexen Ebene, während die Funktion Bi (x) hat auch unendlich viele Nullen im Sektor {z ∈ C. : π / 3 <| arg (z) | <π / 2}.

Grundstücke[edit]

Beziehung zu anderen Sonderfunktionen[edit]

Für positive Argumente beziehen sich die Airy-Funktionen auf die modifizierten Bessel-Funktionen:

${ displaystyle { begin {align} operatorname {Ai} (x) & {} = { frac {1} { pi}} { sqrt { frac {x} {3}} , K_ { frac {1} {3}} left ({ tfrac {2} {3}} x ^ { frac {3} {2}} right), \ operatorname {Bi} (x) & { } = { sqrt { frac {x} {3}}} left (I _ { frac {1} {3}} left ({ tfrac {2} {3}} x ^ { frac {3 } {2}} right) + I _ {- { frac {1} {3}}} left ({ tfrac {2} {3}} x ^ { frac {3} {2}} right ) right). end {align}}}$

Hier, ich_{± 1/3} und K._1/3 sind Lösungen von

${ displaystyle x ^ {2} y ” + xy ‘- left (x ^ {2} + { tfrac {1} {9}} right) y = 0.}$

Die erste Ableitung der Airy-Funktion ist

${ displaystyle operatorname {Ai ‘} (x) = – { frac {x} { pi { sqrt {3}}} , K _ { frac {2} {3}} left ({ tfrac {2} {3}} x ^ { frac {3} {2}} right).}$

Funktionen K._1/3 und K._2/3 kann in Form von schnell konvergierten Integralen dargestellt werden^[4] (siehe auch modifizierte Bessel-Funktionen)

Bei negativen Argumenten bezieht sich die Airy-Funktion auf die Bessel-Funktionen:

${ displaystyle { begin {align} operatorname {Ai} (-x) & {} = { sqrt { frac {x} {9}}} left (J _ { frac {1} {3}} left ({ tfrac {2} {3}} x ^ { frac {3} {2}} right) + J _ {- { frac {1} {3}}} left ({ tfrac { 2} {3}} x ^ { frac {3} {2}} right) right), \ operatorname {Bi} (-x) & {} = { sqrt { frac {x} { 3}}} left (J _ {- { frac {1} {3}}} left ({ tfrac {2} {3}} x ^ { frac {3} {2}} right) – J _ { frac {1} {3}} left ({ tfrac {2} {3}} x ^ { frac {3} {2}} right) right). End {align}}}$

Hier, J._{± 1/3} sind Lösungen von

${ displaystyle x ^ {2} y ” + xy ‘+ left (x ^ {2} – { tfrac {1} {9}} right) y = 0.}$

Die Funktionen des Torschützen Hallo(x) und -Gi(x) Löse die Gleichung y” – xy = 1 / π. Sie können auch in Form der Airy-Funktionen ausgedrückt werden:

${ displaystyle { mathcal {F}} ( operatorname {Ai}) (k): = int _ {- infty} ^ { infty} operatorname {Ai} (x) e ^ {- 2 pi ikx} , dx = e ^ {{ frac {i} {3}} (2 pi k) ^ {3}}.}$

Andere Verwendungen des Begriffs Airy-Funktion[edit]

Durchlässigkeit eines Fabry-Pérot-Interferometers[edit]

“Luftige Funktion” im Sinne der Fabry-Pérot-Interferometer-Durchlässigkeit.

Die Transmissionsfunktion eines Fabry-Pérot-Interferometers wird auch als bezeichnet Luftige Funktion::^[5]

${ displaystyle T_ {e} = { frac {1} {1 + F sin ^ {2} ({ frac { delta} {2}})}},}$

wo beide Oberflächen Reflexionsvermögen haben R. und

${ displaystyle F = { frac {4R} {(1-R) ​​^ {2}}}}$

ist der Finesse-Koeffizient.

Beugung auf einer kreisförmigen Öffnung[edit]

“Luftfunktion” im Sinne der Beugung an kreisförmiger Apertur.

Unabhängig davon wird als dritte Bedeutung des Begriffs die Form der Airy-Scheibe, die sich aus der Wellenbeugung an einer kreisförmigen Apertur ergibt, manchmal auch als bezeichnet Luftige Funktion (siehe zB hier). Diese Art von Funktion ist eng mit der Bessel-Funktion verwandt.

Geschichte[edit]

Die Airy-Funktion ist nach dem britischen Astronomen und Physiker George Biddell Airy (1801–1892) benannt, der sie in seinem frühen Studium der Optik in der Physik (Airy 1838) kennengelernt hat. Die Notation Ai (x) wurde von Harold Jeffreys vorgestellt. Airy war 1835 britischer Astronom Royal geworden und hatte diesen Posten bis zu seiner Pensionierung 1881 inne.

Siehe auch[edit]

Verweise[edit]

• Abramowitz, Milton; Stegun, Irene Ann, Hrsg. (1983) [June 1964]. “Kapitel 10”. Handbuch der mathematischen Funktionen mit Formeln, Graphen und mathematischen Tabellen. Angewandte Mathematik. 55 (Neunter Nachdruck mit zusätzlichen Korrekturen des zehnten Originaldrucks mit Korrekturen (Dezember 1972); erste Ausgabe). Washington, D.C; New York: Handelsministerium der Vereinigten Staaten, National Bureau of Standards; Dover-Veröffentlichungen. p. 446. ISBN 978-0-486-61272-0. LCCN 64-60036. HERR 0167642. LCCN 65-12253.
• Airy (1838), “Über die Intensität des Lichts in der Nähe eines Ätzmittels”, Transaktionen der Cambridge Philosophical Society, Universitätspresse, 6: 379–402, Bibcode:1838TCaPS … 6..379A
• Frank William John Olver (1974). Asymptotik und Sonderfunktionen, Kapitel 11. Akademische Presse, New York.
• Drücken Sie, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), “Abschnitt 6.6.3. Luftige Funktionen”, Numerische Rezepte: Die Kunst des wissenschaftlichen Rechnens (3. Aufl.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
• Vallée, Olivier; Soares, Manuel (2004), Luftige Funktionen und Anwendungen für die Physik, London: Imperial College Press, ISBN 978-1-86094-478-9, HERR 2114198, archiviert von das Original am 13.01.2010abgerufen 2010-05-14

Externe Links[edit]

• “Luftige Funktionen”, Enzyklopädie der Mathematik, EMS Press, 2001 [1994]
• Weisstein, Eric W. “Luftige Funktionen”. MathWorld.
• Wolfram-Funktionsseiten für Ai und Bi Funktionen. Enthält Formeln, Funktionsauswerter und Plotrechner.
• Olver, FWJ (2010), “Luftige und verwandte Funktionen”in Olver Frank WJ; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (Hrsg.), NIST-Handbuch für mathematische Funktionen, Cambridge University Press, ISBN 978-0-521-19225-5, HERR 2723248